1. 고체의 결정구조
1.0 과목 소개
이 과목에서 다루는 내용들
이 책에서는 반도체 재료 및 소자의 전기적 특성을 다룬다.
그래서 고체의 전기적 특성이 중요하다. 반도체는 일반적으로 단결정 물질이다.
단결정 물질의 전기적 특성은 화학 조성뿐만 아니라 고체의 원자 배열에 의해 결정된다.
그래서 고체의 결정 구조에 대한 대략의 연구가 필요하다.
추가적으로 단결정 물질의 형성 또는 성장은 반도체 기술의 중요한 부분이다.
이 장에서 다루는 내용은 다음과 같다.
• 반도체 물질의 열거 및 기술
• 고체의 세가지 종류 : amorphous, polycrystalline, and single crystal
• 세가지 단순한 결정 구조들, 결정면, 다이아몬드 구조
• 원자결합(Atomic bonding)
• 고체에서 다양한 imperfections and impurities
• 단결정 반도체 물질을 생성하는 몇가지 방법
• Silicon에서 산화물의 형성
• Python의 기초
1.1 반도체 물질들
• 반도체는 금속과 절연체 사이의 전도성을 갖는 물질의 그룹
• 반도체의 두 가지 일반적인 분류
- 원소 반도체 재료: Si(가장 많이 쓰임), Ge
- 화합물 반도체 재료: GaAs(광소자, 고속의 특수응용분야), Al$_x$Ga$_{1-x}$As, GaP
| Period/Group | II | III | IV | V | VI |
| 2 | B Boron | C Carbon | N Nitrogen | O Oxygen |
|
| 3 | Al Aluminum | Si Silicon | P Phosphorus | S Sulfur |
|
| 4 | Zn Zinc | Ga Gallium | Ge Germanium | As Arsenic | Se Selenium |
| 5 | Cd Cadmium | In Indium | Sn Tin | Sb Antimony | Te Tellurium |
| 6 | Hg Mercury |
| Elemental semiconductors | IV compound semiconductors | ||
| Si | Silicon | SiC | Silicon carbide |
| Ge | Germanium | SiGe | Silicon germanium |
| Binary III-V compounds | Binary II-VI compounds | ||
| AlAs | Aluminum arsenide | CdS | Cadmium sulfide |
| AlP | Aluminum phosphide | CdTe | Cadmium telluride |
| AlSb | Aluminum anitimonide | HgS | Mercury sulfide |
| GaAs | Gallium arsenide | ZnS | Zinc sulfide |
| GaP | Gallium phosphide | ZnTe | Zinc telluride |
| GaSb | Gallium anitimonide | ||
| InAs | Indium arsenide | ||
| InP | Indium phosphide | ||
| Ternary compounds | Quaternary compounds | ||
| Al$_x$Ga$_{1-x}$As | Aluminum gallium arsenide | Al$_x$Ga$_{1-x}$As$_y$Ab$_{1-y}$ | Aluminum gallium arsenic anitimonide |
| GaAs$_{1-x}$P$_x$ | Gallium arsenic phosphide | Ga$_x$In$_{1-x}$As$_{1-y}$P$_y$ | Gallium indium arsenic phosphide |
1.2 고체의 종류들
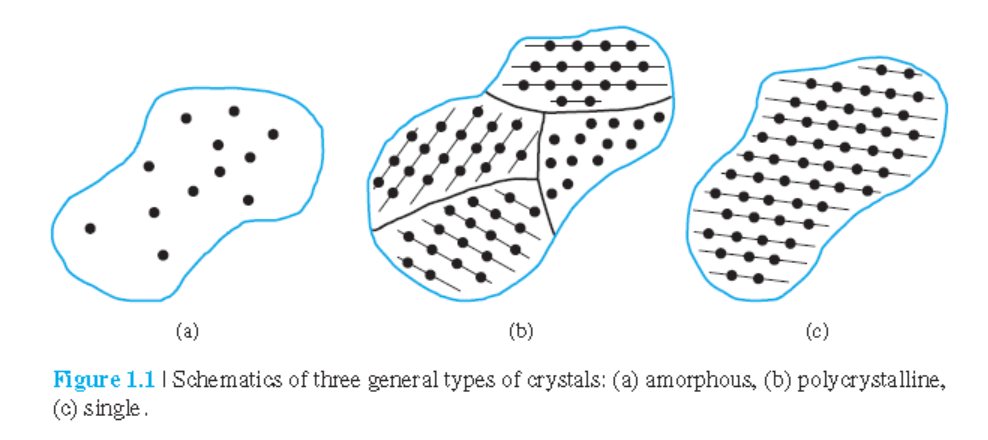
• 고체의 세가지 종류
amorphous(비정질), polycrystalline(다결정), single crystal(단결정)
• amorphous: 몇 가지 원자 또는 분자 차원 내에서만 질서를 가짐
• polycrystalline: 많은 원자 또는 분자 차원에서 높은 질서가짐.
단결정 영역은 서로에 대해 크기와 방향이 다양함.
단결정 영역을 grain이라고도 하며 grain 경계에 의해 서로 분리됨.
• 단결정 재료는 이상적으로 재료의 전체 부피에 걸쳐 높은 주기성을 가짐.
다결정 재료는 grain 경계가 전기적 특성을 저하시키는 경향이 있는데,
그에 비해 단결정 재료는 전체 부피에 걸쳐 주기성을 가져서 비단결정 재료에 비해 전기적 특성이 우수함.
 |
 |
 |
| 비정질(armorphos) | 다결정(polycrystal) | 단결정(single crystal) |
1.2 공간격자들(Space Lattices)
1.2.1 원시셀과 단위셀(Primitive and Unit Cell)
lattice point(격자점)과 translation으로 특정 원자 배열을 나타냄.
그림 1.2처럼 거리 $a_1$ 및 거리 $b_1$의 반복된 확장.
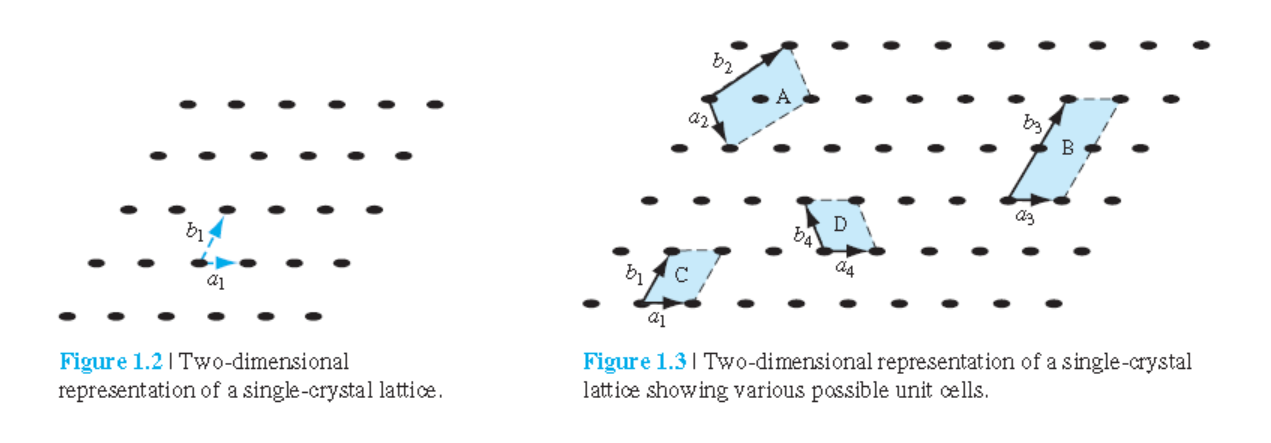
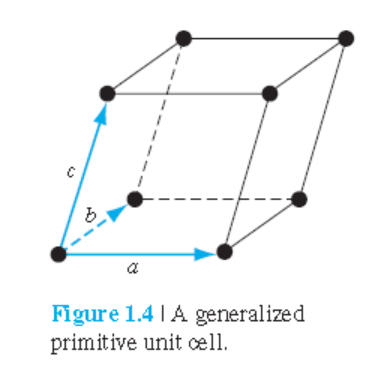
• Unit cell : 격자를 형성하기 위해 필요한 작은 부피.
• Primitive cell : 가장 작은 unit cell
3차원 결정에서 모든 등가 lattice point들은 다음식으로 얻어질 수 있다.
$$ \vec{r}=p\vec{a} + q\vec{c} + s\vec{c}$$
여기서 p, q, s는 정수. a, b, c는 unit cell lattice constant들.
1.2.2 기본적인 결정 구조들
• 반도체 결정에 대해 논의하기 전에 세 가지 결정 구조를 공부하자.
그림 1.5는 simple cubic(sc), body-centered cubic(bcc), and face-centered cubic(fcc) 구조를 보여준다.
$\vec{a}$, $\vec{b}$, $\vec{c}$는 서로 수직이고 길이는 같다.
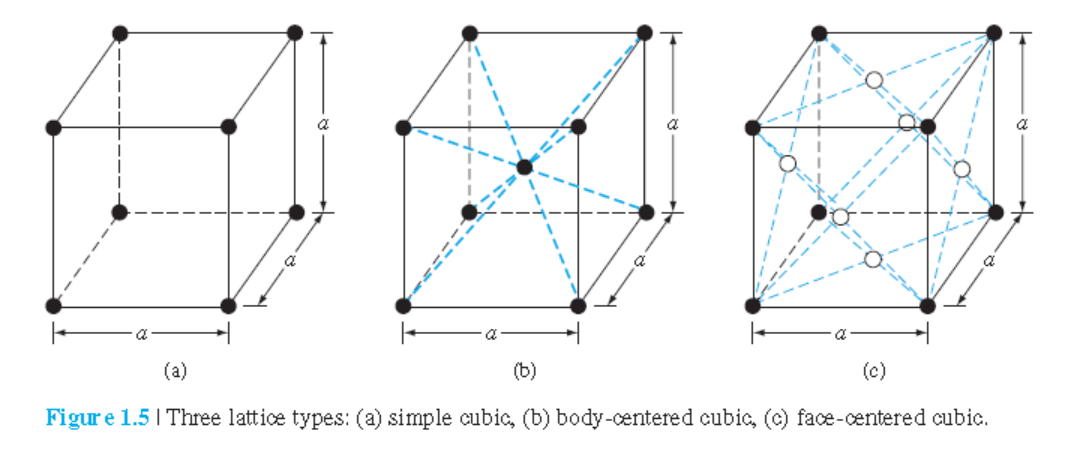
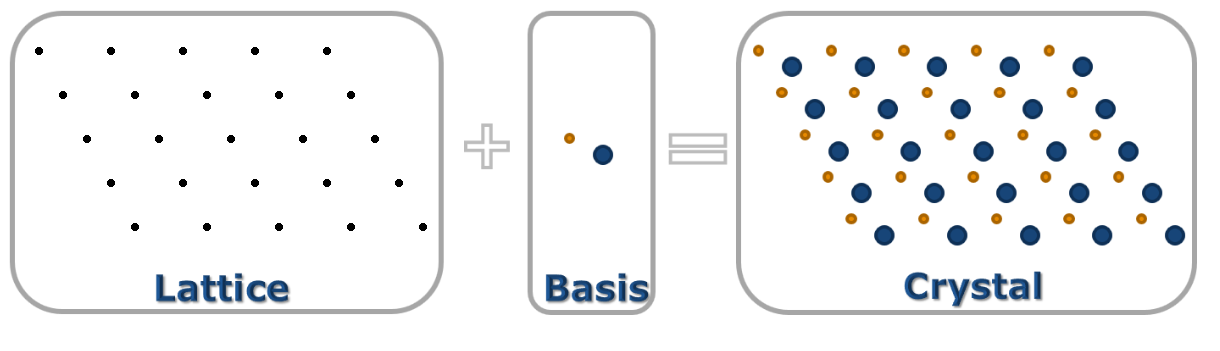
 • 결정은 lattice와 basis의 결합으로 이루어진다.
• 결정은 lattice와 basis의 결합으로 이루어진다.
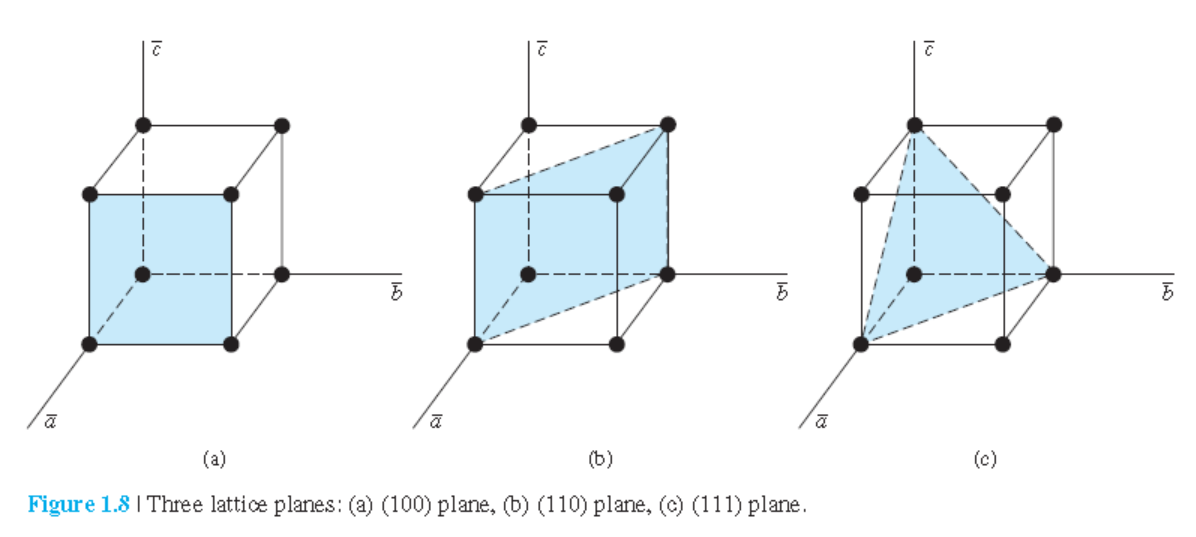
1.2.3 결정면들과 밀러 지수(Miller Indices)


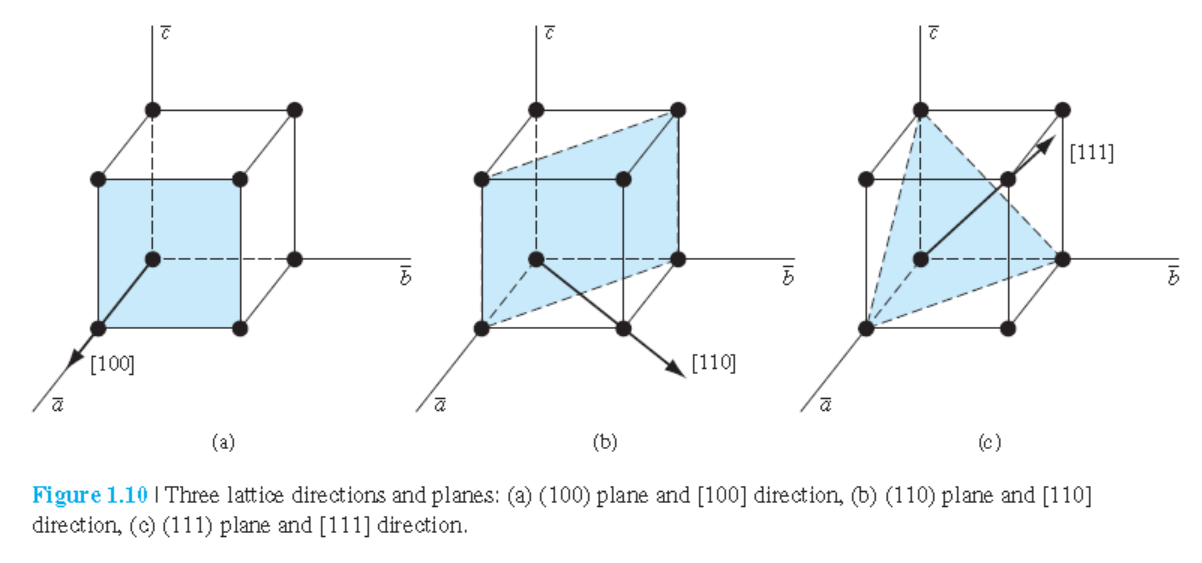
1.2.4 결정내에서 방향들
[hkl] 방향은 (hkl) 평면에 수직
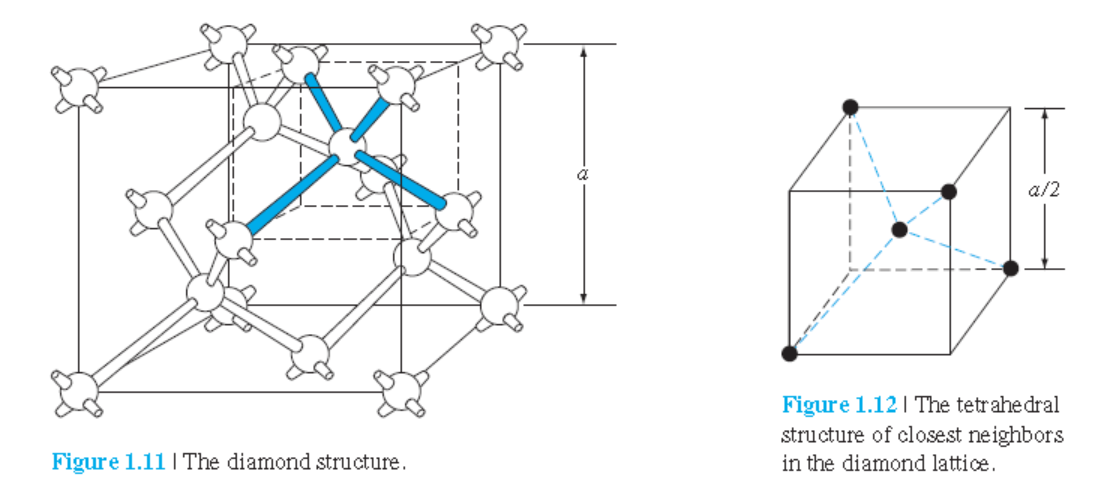
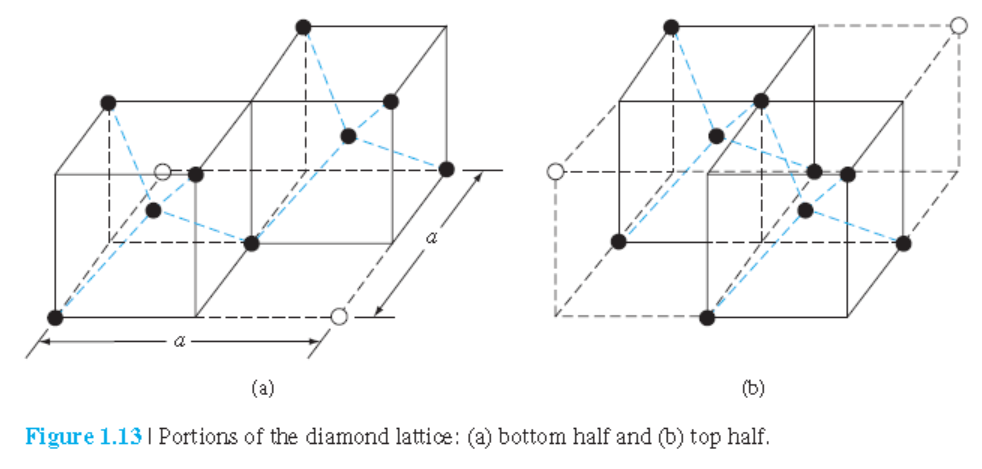
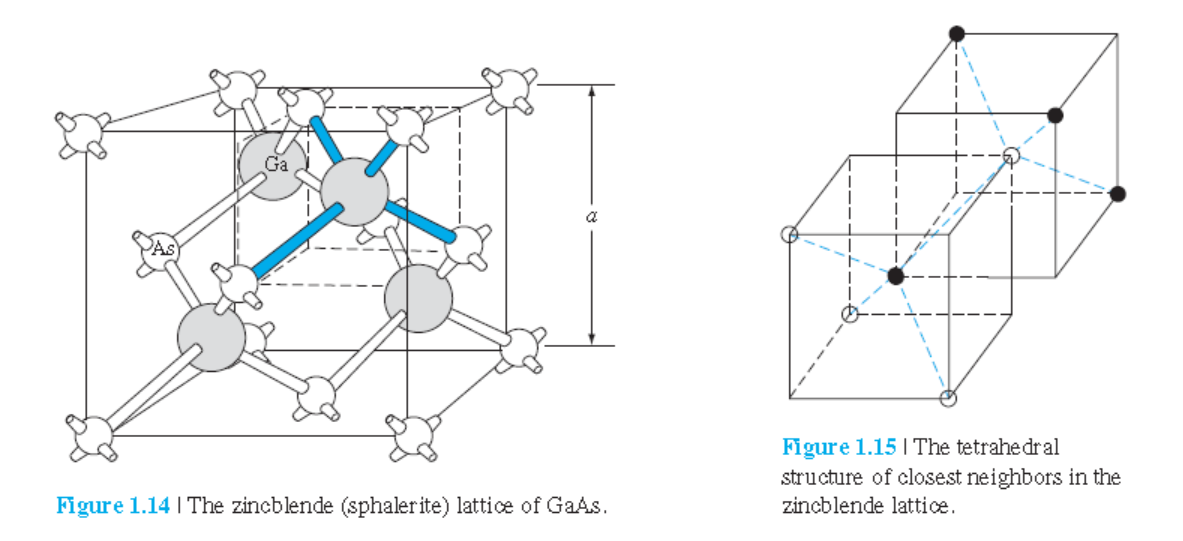
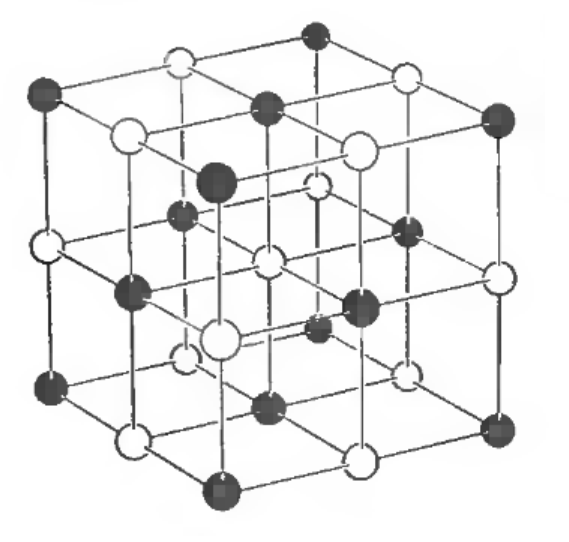
1.2.5 다이아몬드 구조
Diamond 구조: Si, Ge, C
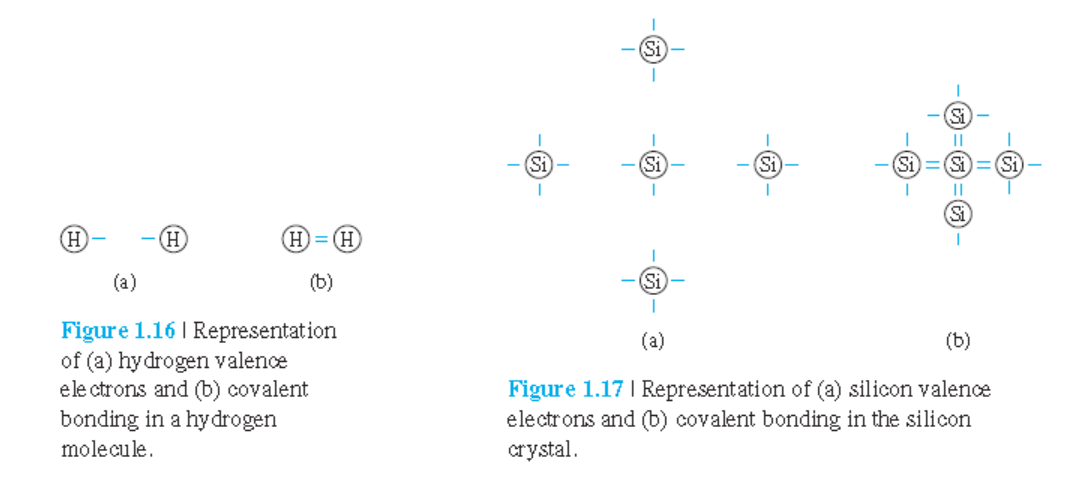
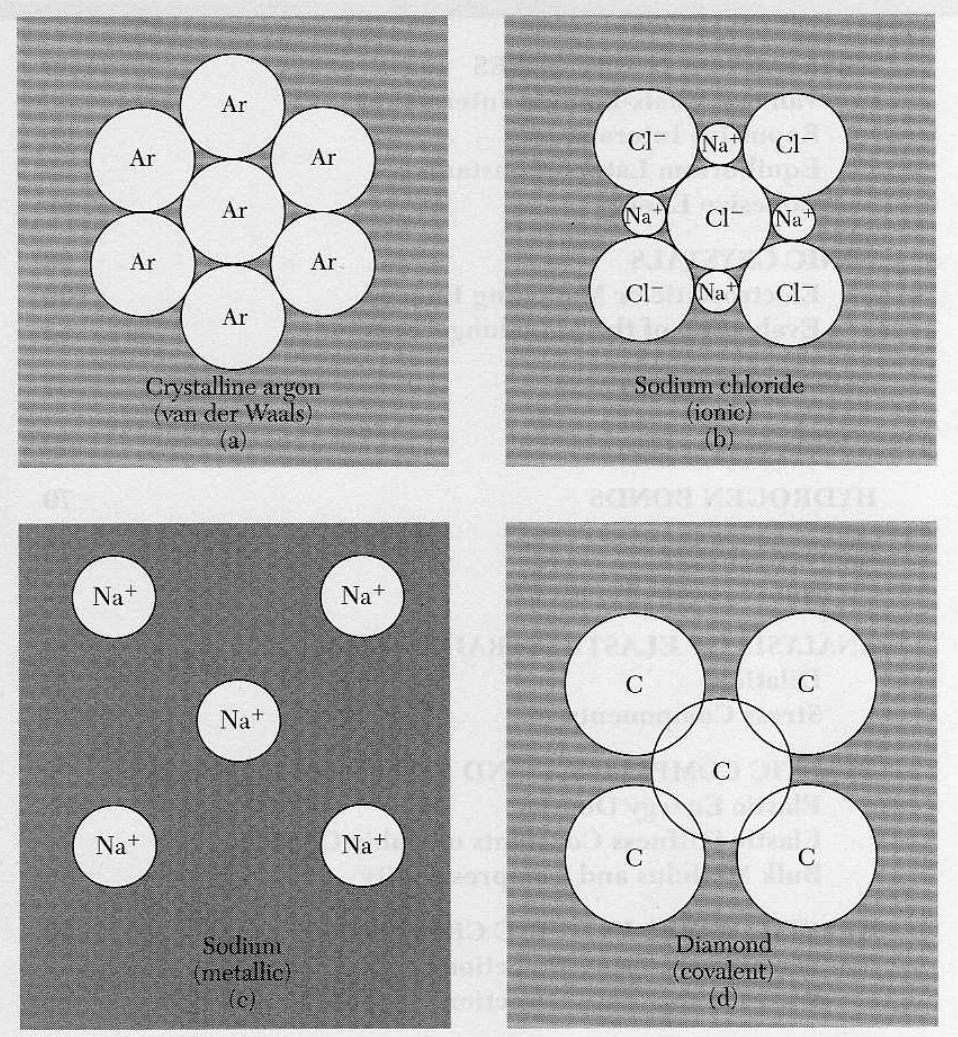
1.3 원자 결합
4가지 결합 형태
Ionic bond (이온 결합)
Covalent bond (공유 결합)
Metallic bond (금속 결합)
Van der Waals bond(반데어발스 결합)
Octet rule
1.4 고체에서 결함(Imperfections)과 불순물(Impurities)
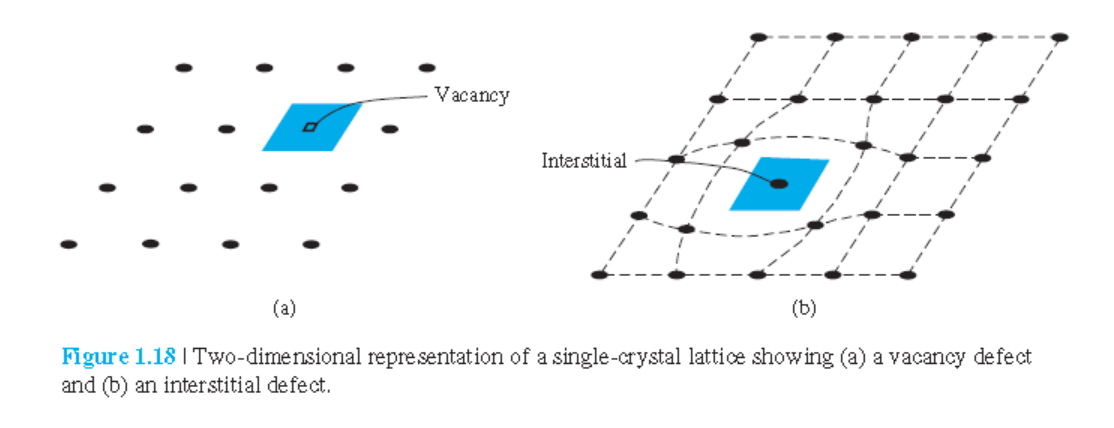
1.4.1 고체에서 결함(Imperfections)
Thermal vibration
Point defect
Vacancy
Interstitial
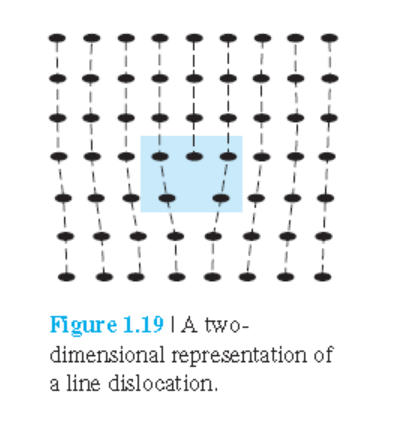
Line defect
Line dislocation
1.4.2 고체에서 불순물
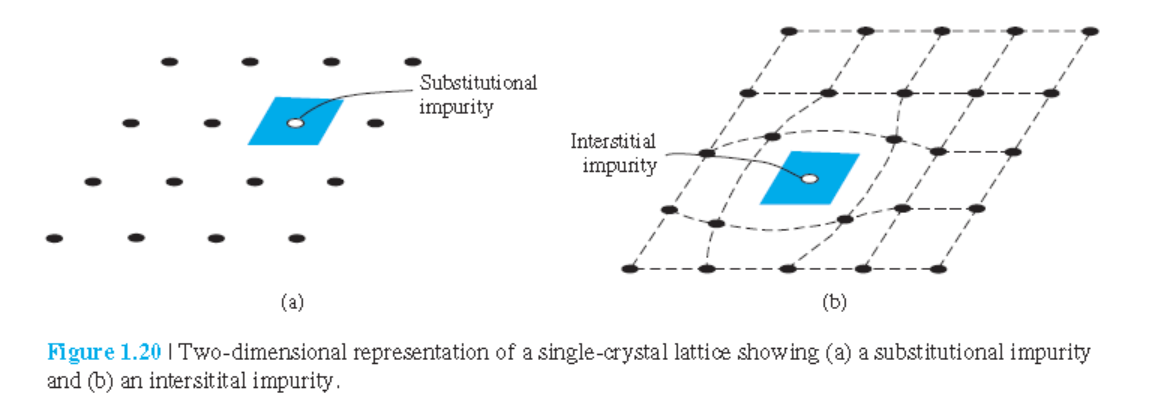
Substitutial impurity
Interstitial impurity
Doping: diffusion, ion implantation
1.5 반도체 물질의 성장
1.5.1 Growth from a Melt
Czochralski 법
1.5.2 Epitaxial Growth
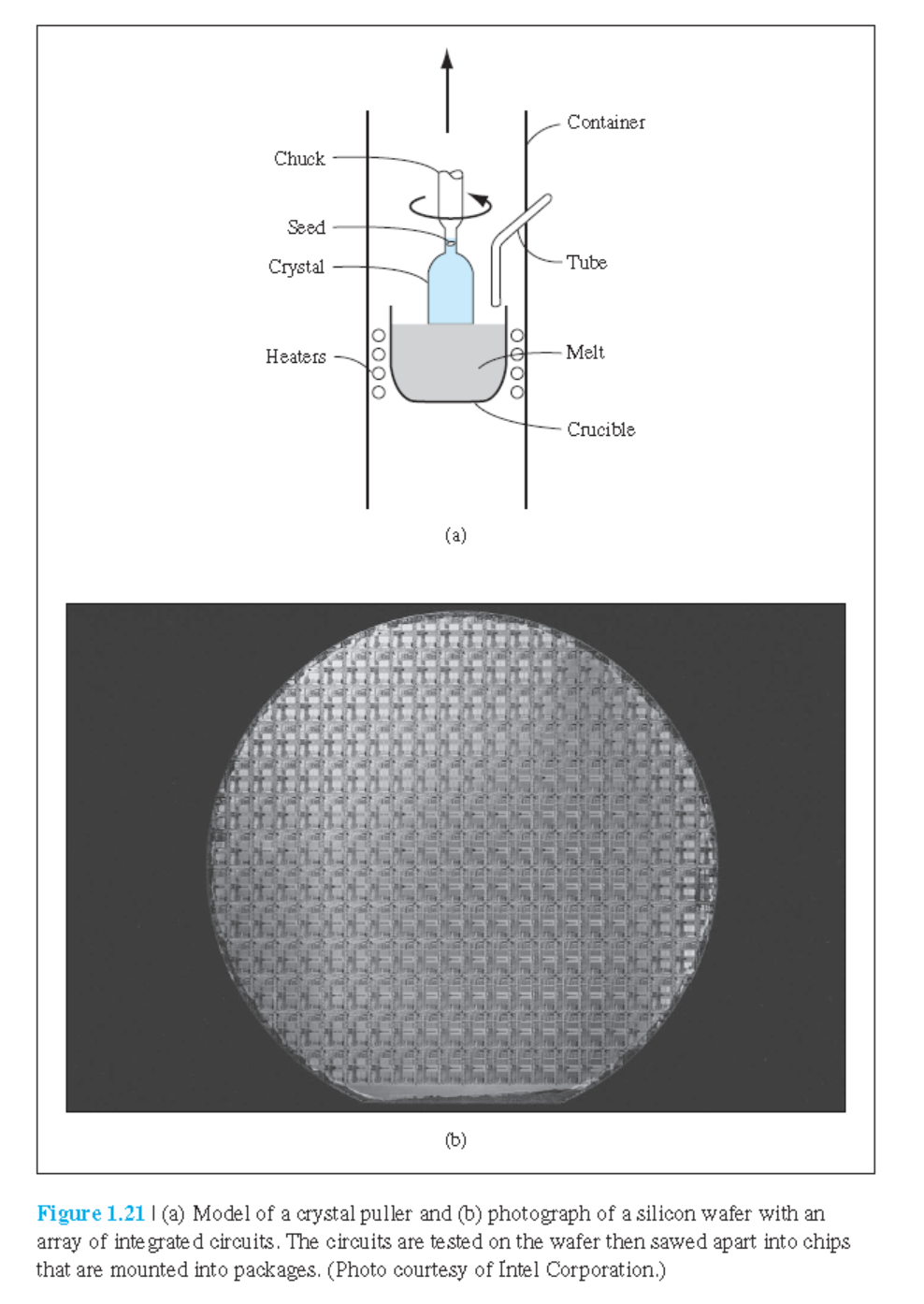
• wafer 제조과정
• 컴퓨터가 계산하는 방법
1.6 Python의 기초
# print문
print(5)
= 기호
# =는 양변이 같다는 듯이 아니라 우변의 값을 좌변에 대입한다는 뜻이다.
a = 5
print(5)
변수와 상수
# 전통적으로 위 경우 우변의 수를 상수 좌변의수를 변수라고 함. 위 문장을 치환문이라고 한다.
사칙연산
a = 5
b = 4
c = a + b
print(c)
print("{0}와 {1}의 합은 {2}이다.".format(a,b,c))
# 변수 이름짓기, 가능한 알기 쉽게..
N_items = 7
print(N_items)
# # 주석 표시
# 여러줄을 한줄로 쓰기
a = 5 ; b = 4; c = a + b
print("{0}와 {1}의 합은 {2}이다.".format(a,b,c))
# 한줄을 여러줄로 쓰기
a = 5 ; b = \
4; c = a + b
print("{0}와 {1}의 합은 {2}이다.".format(a,b,c))
# 잘모르는 것은 인터넷 구글에서 찾아보기
# 본인이 다 학습할 수 있음
# 확장 치환문
# += , -= *=, /= , //=, %=, **= , >>= , < < = , &= , ^= , &=, !=
a = 5
a += 7 # a = a + 7 과 같음
print(a)
# 자료형의 종류
# bool, int, float, complex, str, bytes, list, dic, tuple, set
# bool, 정수로도 간주 가능 , True == 1, False == 0
a = 5
b = 3
print(a > b)
print(a < b)
print(a==b)
c = True
print(c)
# complex
d = 5 + 7j
e = 1 + 3j
print(d+e)
# list: 순서있는 파이썬 객체의 집합
a_list = [1,2,3,4,5,6,7,8]
print(a_list[0], a_list[1], a_list[2])
print('a_list[2:5]', a_list[2:5])
print('a_list[-1]', a_list[-1])
b_list = [8,9,0,11,12,24]
print('a_list+b_list', a_list + b_list)
# list의 메서드: append, del, reverse, sort
b_list = [8,9,0,11,12,24]
b_list.sort()
print('b_list.sort()', b_list)
# dic: 순서없는 파이썬 객체의 집합
a_dic = {'철수': 4, '민희':5, '영훈':6}
print(a_dic['철수'], a_dic['민희'], a_dic['영훈'])
# tuple: 순서있는 파이썬 객체의 집합, 내용변경이 안됨
a_tuple = ('철수','민희','영훈')
print(a_tuple[0], a_tuple[1], a_tuple[2])
# set: 순서있는 파이썬 객체의 집합, 내용변경이 안됨
a_set = {7,8,9}
b_set = {9,10,11}
print(a_set, b_set)
print("합집합", a_set.union(b_set))
print("교집합", a_set.intersection(b_set))
# 문자열 편집
e = "Who are you?"
print(e[2:6])
print(e[2:])
print(e[:6])
# 문자열 연산
d = "Hello world"
e = "Who are you?"
print(d+e)
print(d*4)
# 문자열의 길이
d = "Hello world"
e = "Who are you?"
print(len(d), len(e))
# 문자열 검사
d = "Hello world"
print("llo" in d)
print("llt" in d)
# 문자열 메서드 upper, split, find, startwith, endswitch
e = "Who are you?"
e_arr = e.split(" ")
print(e_arr[0])
print(e_arr[1])
print(e_arr[2])
# byte 문자열
bb= b'Pyton Lecture'
print(bb);
dd = bb.decode() ; print(dd)
ee = dd.encode() ; print(ee)
# 조건문
# 내부 즐럭 한단 뒤로 띄움, 같은 빈칸 유지
a = 5
b = 3
if a>b:
print('a가 b보다 크다.')
else :
print('a가 b보다 작다.')
# 반복문
for i in [1,2,3,4,5]:
print(i)
for i in range(1,6):
print(i)
i=0
while i < 6 :
print(i)
i+=1
# 파일
file0 = open('output.txt', 'w')
file0.write('Hello ~ ~ ~')
file0.close()
# with 문
with open('output_1.txt', 'w') as file2:
file2.write('Hello 2 ~ ~ ~')
# 함수
def add(a,b):
c = a + b
d = "a와 b의 합은 " + str(c) + "입니다."
return d
print(add(3,4))
# 클래스: 변수와 함수를 묶은 단위
# 클래스 : 붕어빵 틀
class A1:
scale = 10 # 멤버
def __init__(self):
print('이것은 클래스 A입니다.')
def add(self, c,d): # 메서드
return "클래스 합" + str(c+d)
instans_a = A1() # instance(객체) 생성 붕어빵
print(instans_a.add(3,4))
instans_a1 = A1() # instance(객체) 생성 붕어빵
instans_a2 = A1() # instance(객체) 생성 붕어빵
instans_a3 = A1() # instance(객체) 생성 붕어빵
# math 모듈 사용
import math
print(math.sqrt(3))
print(math.sin(3))
print(math.pi)
# numpy 모듈 소개
import numpy as np
# Generate some random data
data = np.random.randn(2, 3)
print('data' , data )
print('data*10' , data*10 )
print('data+data', data+data)
print('data.shape', data.shape)
print('data.dtype', data.dtype)
# numpy 배열 생성
data1 = [6, 7.5, 8, 0, 1]
arr1 = np.array(data1)
print(arr1)