1. 과목 소개 및 기초 수학

1.0 과목 소개

이 과목에서 다루는 내용들
• 전하

• 전기장

• 전류

• 자기장

• 시간의존 자기장 -> 전기장

• 시간의존 전기장 -> 자기장

• 전자기유도

• 전자기파

• 복사

1.1 미분과 적분

1.1.1 미분

속도는 $x$-$t$ 그래프에서 기울기로 표현할 수 있다.

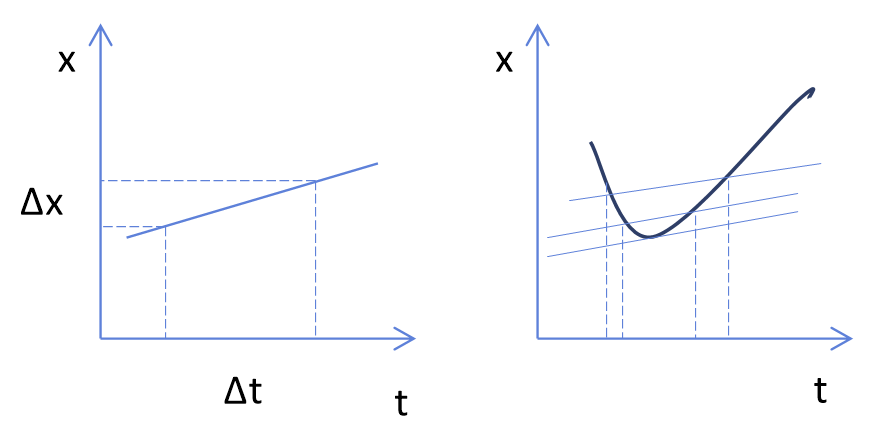
그림 1-1
등속도로 가는 경우
$$ v=\frac{\Delta x}{\Delta t} $$ 속도가 변하는 경우
$$ v_{\textrm{순간}}=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} $$ 평균 속도는 $x$-$t$ 그래프에서 두 점사이의 기울기
순간 속도는 $x$-$t$ 특정 시간에서 접선의 기울기 -> 미분

(예제) $x^3$의 미분이 $3x^2$임을 증명하라.
$x$가 $\Delta x$ 만큼 변할 때 $x^3$는 $(x+\Delta)^3$ 만큼 변한다. \begin{aligned} &\lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^3 - x^3}{(x+\Delta x)-x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{x^3 + 3 x^2 \Delta x + 3 x (\Delta x)^2 + (\Delta x)^3- x^3 }{\Delta x}\\ &= \lim_{\Delta x \rightarrow 0} \left(3 x^2 + 3 x (\Delta x) + (\Delta x)^2\right) \\ &= 3 x^2 \end{aligned}

1.1.2 적분

변위는 $v$-$t$ 그래프에서 그래프 아래의 면적으로 표현할 수 있다.

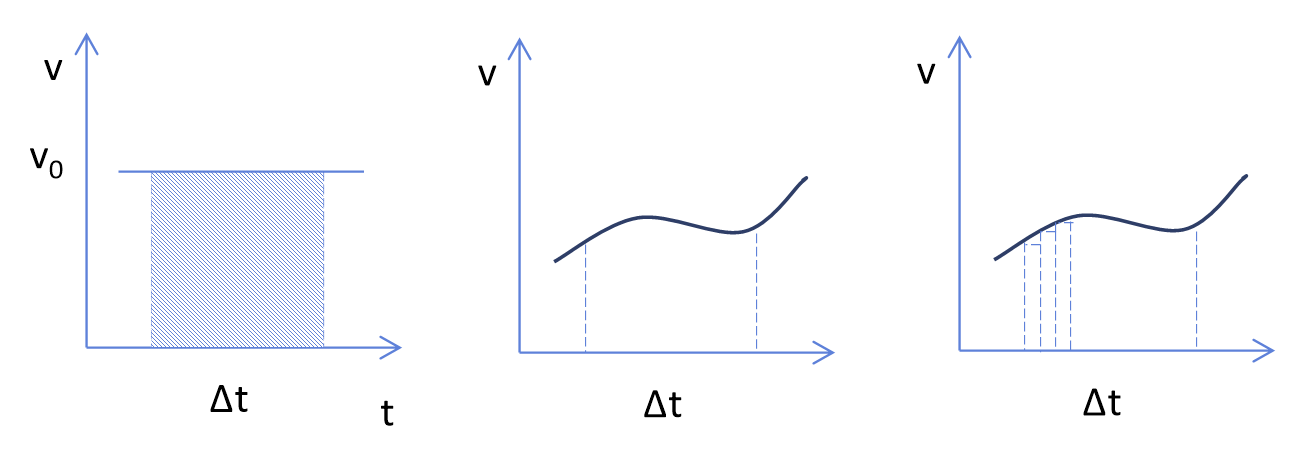
그림 1-2
등속도로 가는 경우
$$ \Delta x = v_0 \Delta t $$ 속도가 변하는 경우
그래프 아래 부분을 수많은(N개) 직사각형으로 나눈다.
$$ 그래프아래 면적 = v_1 \Delta t + v_2 \Delta t + \cdots $$ $$ 그래프아래 면적 = \sum_{i=1}^{N} v_i \Delta t $$ $$ 그래프아래 면적 = \lim_{N \to \infty}\sum_{i=1}^{N} v_i \Delta t $$ $$ 그래프아래 면적 = \int_{t_1}^{t_2} v d t $$

1.2 좌표계

물리현상을 편리하게 설명하기 위한 도구로 좌표계가 이용된다. 여기서는 직각 좌표계, 원통 좌표계, 구 좌표계에 대해서 알아본다.

1.2.1 직교 좌표계

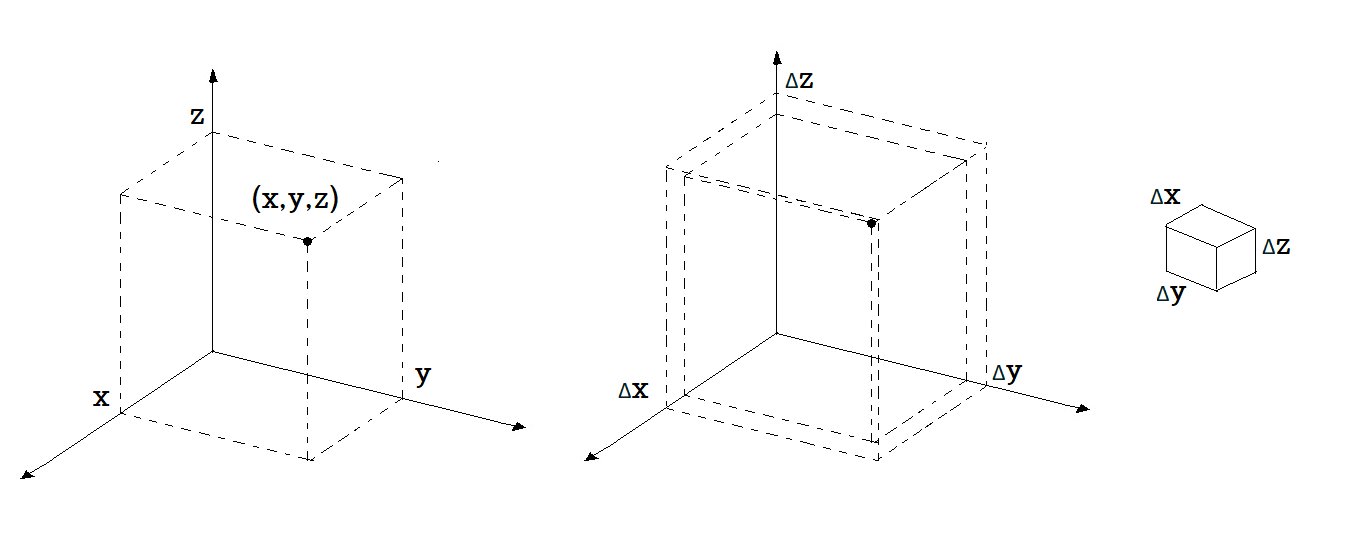
그림 1-3
$$dV = dx dy dz$$

1.2.2 원통 좌표계

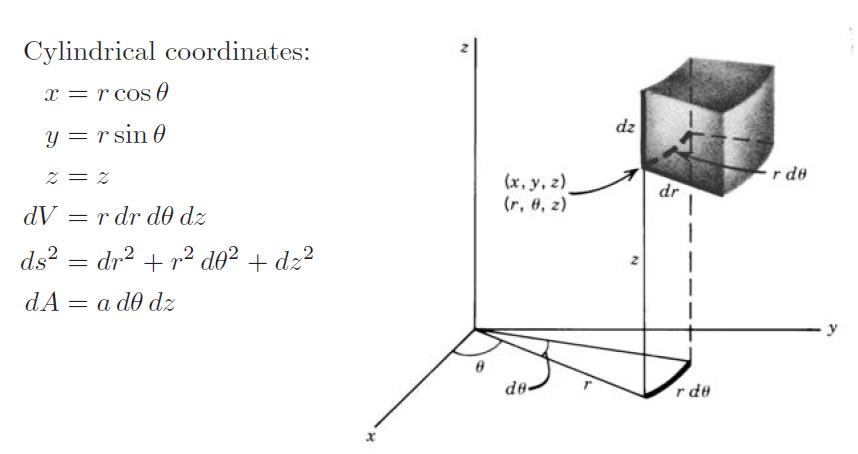
그림 1-4

1.2.3 구 좌표계

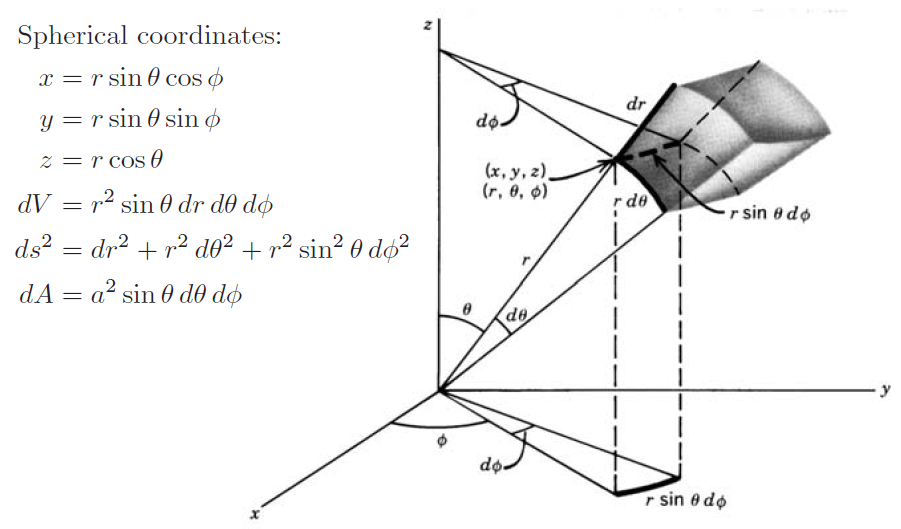
그림 1-5

(예제) 좌표계에 따른 적분

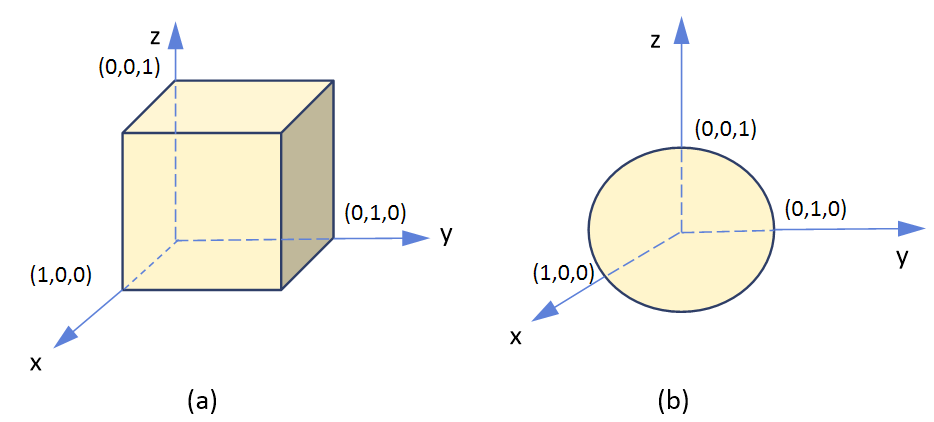
위 그림과 같이 주어지는 부피가 있다.
그림 (a)의 부피에 대해 $G(x,y,z)= z^2 (x+2)$를 부피 적분하여라.
(풀이)
\begin{aligned} \int\int\int G(x,y,z) dV &=\int_{z_{최소}}^{z_{최대}}\int_{y_{최소}}^{y_{최대}} \int_{x_{최소}}^{x_{최대}} z^2 (x+2) dxdydz \\ &=\int_{0}^{1}\int_{0}^{1} \int_{0}^{1} z^2 (x+2) dxdydz \\ &=\int_{0}^{1}(x+2) dx \int_{0}^{1} dy \int_{0}^{1} z^2 dz \\ &=\left[\frac{x^2}{2} + 2x\right]_0^1 \left[y\right]_0^1 \left[\frac{z^3}{3}\right]_0^1 dz \\ &=(1/2+2)(1/3) \end{aligned}
그림 (b)의 부피에 대해 $G(r,\theta,\phi)= \frac{1}{r\sin\theta}$를 부피 적분하여라.
(풀이)
\begin{aligned} \int\int\int G(r,\theta,\phi) dV &= \int_{0}^{2\pi}\int_{0}^{\pi} \int_{0}^{1}\frac{1}{r\cos\theta} r^2\sin\theta dr d\theta d\phi \\ &= \int_{0}^{2\pi}\int_{0}^{\pi} \int_{0}^{1} r dr d\theta d\phi \\ &= \frac{1}{2} (\pi) (2\pi) \end{aligned}

1.2.4 각 좌표계에서 질량 구하기

질량의 정의 $=$ 밀도 $\times$ 부피
밀도가 균일할 때
$$ m = \rho \times V $$
밀도가 불균일할 때
$$ m = \int_V \rho dV $$
$\rho$가 어떤 좌표계로 표현되어 있는냐에 따라 적절한 $dV$를 선택한다.

1.3 Vector

1.3.1 Vector의 정의와 표기법

• 스칼라와 벡터

Scalar는 크기만 가지고 있는 양이고, vector는 크기와 방향을 가지고 있는 양이다.
Scalar의 예 : 온도, 밀도 등
Vector의 예 : 속도, 가속도 등

• 벡터의 기하 표기법

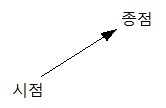그림 1-6
그림 1-6과 같이 벡터는 화살표로 표시하는데 화살표의 길이는 벡터의 크기를 표시하고, 화살표의 방향은 벡터의 방향을 표시한다. 벡터의 출발점은 시점, 도착점은 종점이라고 한다. 벡터를 기호로 표시할 때는 $\vec{A}$ 처럼 문자위에 화살표를 그어서 표시하거나, $\textbf{A}$처럼 굵은 글씨의 문자로 표시한다.

• 벡터량의 동일성


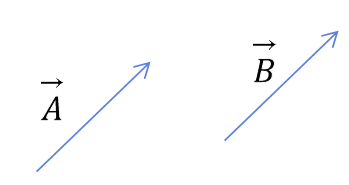
그림 1-7
벡터는 크기와 방향을 가진 양으로서 크기와 방향이 같다면 같은 량의 벡터이다. 그림과 같이 $\vec{A}$와 $\vec{B}$ 두 벡터가 다른 장소에 있지만, 크기와 방향이 동일하기 때문에 같은 량의 벡터이다.

• 벡터의 성분표시법


그림 1-8
벡터가 있는 공간에 $x$-$y$ 좌표축을 설정해주면 벡터를 더 체계적으로 표시할 수 있다. 그림8과 같이 $x$축에 수직하게 빛을 비출때 x축에 나타나는 $\vec{A}$의 그림자의 길이를 $\vec{A}$의 $x$성분이라 하고, $A_x$로 표시한다. 유사하게 $y$축에 수직하게 빛을 비출때 $y$축에 나타나는 $\vec{A}$의 그림자의 길이를 $\vec{A}$의 $y$성분이라 하고, $A_y$로 표시한다. 만약 벡터의 시점의 좌표가 $(x_1, y_1)$이고, 종점의 좌표가 $(x_2, y_2)$라면, $A_x=x_2-x_1$와 $A_y=y_2-y_1$가 성립한다.


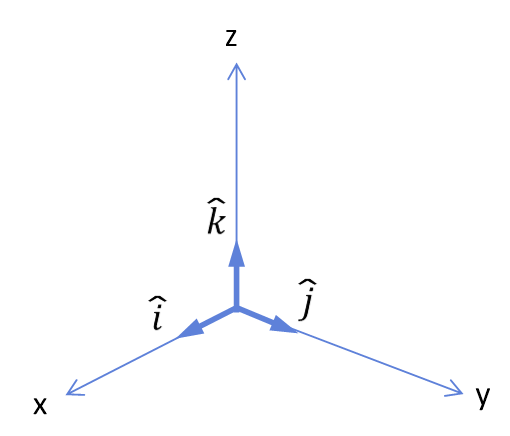
그림 1-9
단위 벡터의 정의
$\hat{i}$ : $+x$방향으로 향하는 크기가 1인 벡터
$\hat{j}$ : $+y$방향으로 향하는 크기가 1인 벡터
$\hat{k}$ : $+z$방향으로 향하는 크기가 1인 벡터
이들 벡터는 크기가 1이기 때문에 단위벡터라고 불린다.
그러면 $\vec{A}$는 $A_x \hat{i}$와 $A_y \hat{j}$의 합(평행사변형법 참고)이기 때문에 다음과 같이 표시될 수 있다.
$\vec{A}=A_x \hat{i}+A_y \hat{j}$
벡터는 크기와 방향을 가진 양으로서, 성분표시법이 벡터의 완전한 표시법이 되는 이유는 그 성분들만 가지고도 벡터의 크기와 방향이 결정될 수 있기 때문이다.
벡타의 크기: $A=\sqrt{A_x^2+ A_y^2}$
벡터의 방향은 각도로 표시 : $\tan\theta =A_y/A_x$ 또는 $\theta =\tan^{-1}(A_y/A_x)$
여기서 $\theta$는 $\vec{A}$와 $x$축이 이루는 각도이다.
벡터의 성분표시를 3차원으로 확장해보자. 그러면 $xy$ 평면에 수직한 $z$축이 추가되어야한다. $xy$ 평면에 수직한 방향은 두가지가 있는데, 그림과 같이, 오른손으로 $x$축에서 $y$축을 감았을때 엄지 손가락이 향하는 방향을 $+z$축으로 잡는다. 이 좌표계를 오른손 좌표계라고 한다. $\vec{A}$의 $z$성분을 $A_z$라 하고, $z$축을 향하는 크기가 1인 단위벡터 $\hat{k}$을 도입하면, $\vec{A}$는 다음과 같이 표시된다.
$\vec{A}=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}$
벡터의 크기는 $A=\sqrt{A_x^2+ A_y^2+A_z^2}$이고,
벡터가 $x,y,z$축과 이루는 각 $\alpha$, $\beta$, $\gamma$는 각각 다음과 같이 주어진다. 그림 x 참조.
$\cos \alpha =A_x/A$
$\cos \beta =A_y/A$
$\cos \gamma =A_z/A$


• $\vec{0}$ 벡터

크기가 0인 벡터를 $\vec{0}$ (영) 벡터라고 한다. $\vec{0}=0 \hat{i}+0\hat{j}+0\hat{j}$. $\vec{0}$를 0이라고 쓴다고해서 벡터 방정식에서는 큰 혼동은 없으므로 종종 그냥 0이라고 표기한다.

1.3.2 vector의 연산

• vector의 덧셈


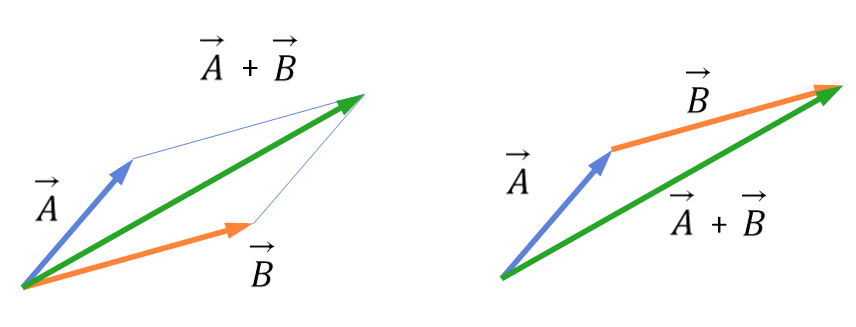
그림 1-10
평행사변형법
그림10처럼 $\vec{A}$와 $\vec{B}$의 시점을 일치시킬때 나타나는 평행사변형의 대각선이 $\vec{A}+\vec{B}$의 결과이다.
그림과 같이 $\vec{A}$, $\vec{B}$ 두 벡터가 있다고 하자. 그러면 $\vec{A}+\vec{B}$, 이 덧셈의 결과는 그림 10의 $\vec{C}$와 같다. 즉, $\vec{A}$의 종점에 $\vec{B}$의 시점을 연결한 후, $\vec{A}$의 시점에서 $\vec{B}$의 종점까지를 연결한 벡터가 $\vec{A}+\vec{B}$의 결과이다. (주의, 벡터의 덧셈은 벡터사이에서만 정의되지 스칼라와 벡터사이의 덧셈은 정의되지 않는다. a+$\vec{B}$ (X) ) 벡터의 덧셈 (성분표시법)
$\vec{C}$가 $\vec{A}$와 $\vec{B}$의 합벡터라고 하자. $\vec{A}+\vec{B}=\vec{C}$. 이 연산을 그림으로 그려보면, 그림 10과 같이 $\vec{A}$의 $x$성분 $A_x$와 $\vec{B}$의 $x$성분 $B_x$의 합이 $\vec{C}$의 $x$성분 $C_x$와 같다는 것을 알 수 있다. 즉, $A_x+B_x=C_x$ 이 성립한다. $y$성분도 동일하게 적용하면, $A_y+B_y=C_y$ 이 성립한다. 좀더 일반화해서 말하면, 이것은 벡터방정식의 특징으로서, 벡터방정식 x의 양변은 같은 방향의 성분끼리 같다는 것이다. $\vec{A}+\vec{B}$을 성분표시법으로 쓰면 다음과 같다.
$\vec{A}+\vec{B}=(A_x+B_x) \hat{i}+(A_y+B_y) \hat{j}$.
여러벡터의 합

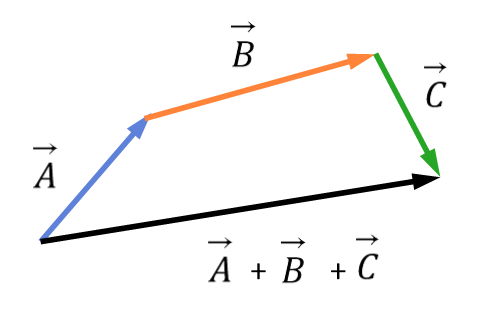
그림 1-11
그림과 같이 $\vec{A}$, $\vec{B}$, $\vec{C}$ 3개의 벡터가 있을 때, 다음 연산의 결과는
$\vec{A}+\vec{B}+\vec{C}$
3개의 벡터를 차례로 연결한 후 $\vec{A}$의 시점에서 $\vec{C}$의 종점을 연결한 벡터가 된다.
성분표시법으로 쓰면 다음과 같다.
$\vec{A}+\vec{B}+\vec{C}=$ $(A_x+B_x+C_x)\hat{i}+(A_y+B_y+C_y)\hat{j}$

• vector의 뺄셈


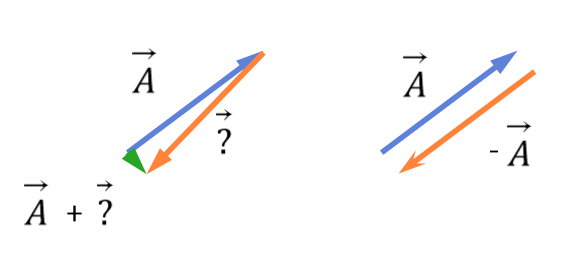
그림 1-12
$\vec{A}$에 어떤 벡터 $\vec{?}$를 더했을 때 0 벡터가 된다면 그 벡터 $\vec{?}$를 $-\vec{A}$로 정의할 수 있을 것이다. 즉 다음 식을 만족하면 $\vec{?}=-\vec{A}$이 성립한다. \begin{eqnarray} \vec{A}+\vec{?}=0 \end{eqnarray} 그림 x를 보면, $\vec{A}$와 $\vec{A}$와 크기는 같은데 방향이 거의 반대인 $\vec{?}$와의 합벡터 $\vec{A}+\vec{?}$가 그려져 있다. 만약 $\vec{?}$의 방향이 완전히 $\vec{A}$와 반대라면 $\vec{A}+\vec{?}=0$을 만족 시킬것이다. 그러므로 $-\vec{A}$는 $\vec{A}$와 크기가 같고 방향이 정반대인 벡터가 된다. 그러면 $\vec{A}-\vec{B}$는 $\vec{A}+(-\vec{B})$로 간주하여 계산한다. 그림 x에 그 결과가 나와있다. 성분 표시법으로 식 x를 만족하는 벡터를 구한다면, $-\vec{A}=-A_x\hat{i} -A_y\hat{j}$가 얻어진다.

• 교환법칙 결합법칙

벡터의 덧셈은 일반 대수연산 처럼 교환법칙과 결합밥칙이 성립한다. 그림 ,,를 보면 $\vec{A}+\vec{B}$의 결과와 $\vec{B}+\vec{A}$의 결과가 같음을 알 수 있다.
$\vec{A}+\vec{B}=\vec{B}+\vec{A}$ (교환법칙)
성분 표시법으로는,
$\vec{A}+\vec{B}$
$=(A_x+B_x)\hat{i}+(A_y+B_y)\hat{j} $
$=(B_x+A_x)\hat{i}+( B_y+A_y)\hat{j}=\vec{B}+\vec{A}$ (교환법칙)
그림 ,,를 보면 $(\vec{A}+\vec{B})+\vec{C}$의 결과와 $\vec{A}+(\vec{B}+\vec{C})$의 결과가 같음을 알 수 있다.
$(\vec{A}+\vec{B})+\vec{C}=\vec{A}+(\vec{B}+\vec{C})$ (결합법칙)
성분 표시법으로는,
$(\vec{A}+\vec{B})+\vec{C}$
$=(A_x+B_x)\hat{i}+(A_y+B_y)\hat{j}+C_x\hat{i}+ C_y\hat{j}$
$=(A_x+B_x+C_x)\hat{i}+(A_y+B_y+C_y)\hat{j}$
$=A_x\hat{i}+ A_y\hat{j}+(B_x+C_x)\hat{i}+ (B_y+C_y)\hat{j}=\vec{A}+(\vec{B}+\vec{C})$
(결합법칙)

• scalar와 vector의 곱셉

벡터에 양의 스칼라를 곱하면 방향은 변하지 않고 크기만 변한다. $\vec{A}$에 2를 곱한 2$\vec{A}$는 크기가 $\vec{A}$의 2배이고 방향은 $\vec{A}$와 동일하다. 성분표시법으로는 2$\vec{A}=2A_x\hat{i}+ 2A_y\hat{j}$로서 $x$, $y$성분도 각각 2배씩 늘어난다. 0.5$\vec{A}$는 크기가 $\vec{A}$의 절반이고 방향은 $\vec{A}$와 동일하다.
성분표시법으로는 0.5$\vec{A}=0.5A_x \hat{i}+ 0.5A_y\hat{j}$.
벡터에 음의 스칼라를 곱하면 방향은 정반대로 바뀌고 크기도 변한다. $-0.5\vec{A}$는 크기가 $\vec{A}$의 절반이고 방향은 $\vec{A}$와 반대인 벡터이다.
성분표시법으로는 -0.5$\vec{A}=-0.5A_x\hat{i}-0.5A_y\hat{j}$.

• vector의 곱셉1(내적)

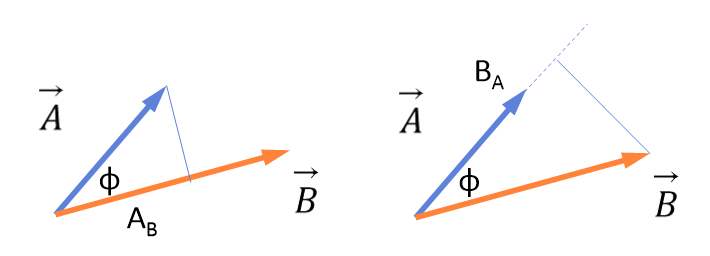
그림 1-13
곱셈의 결과가 스칼라이기 때문에 스칼라곱이라고도 불린다. $\vec{A}$와 $\vec{B}$의 내적은 $\vec{A}\cdot\vec{B}$라고 표기하고 A dot B라고 읽는다. $\vec{A}$와 $\vec{B}$의 내적은 다음과 같이 정의된다.
$\vec{A}\cdot\vec{B}=AB\cos \phi$
여기서 A와 B는 각각 $\vec{A}$와 $\vec{B}$의 크기이고, $\phi$는 두 벡터사이의 각이다. $\vec{A}$와 $\vec{B}$는 그 위치를 서로 바꾸어도 결과 값이 같으므로 두 벡터의 내적은 교환법칙이 성립함을 알 수 있다.
$\vec{A}\cdot\vec{B}=\vec{B}\cdot\vec{A}$
내적의 기하학적 의미를 알아보자.
$\vec{A}\cdot\vec{B}$는 다음 두가지 표현으로 쓸수있다.
$\vec{A}\cdot\vec{B}=(A\cos \phi)B=A(B\cos \phi)$
$A\cos \phi$는 $\vec{A}$의 B방향 성분 $A_B$이고,
$B\cos \phi$는 $\vec{B}$의 A방향 성분 $B_A$이다.
그러므로 $\vec{A}\cdot\vec{B}$는 다음과 같이 쓰는 것도 가능하다.
$\vec{A}\cdot\vec{B}=AB_A=BA_B$
내적의 성분 표시
$\vec{A}$와 $\vec{B}$가 각각 다음과 같이 $x$, $y$, $z$ 성분으로 표시된다고 하자.
$\vec{A}=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}$
$\vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k}$
이 두 벡터의 내적을 시행하기 위해서는 단위벡터들 사이의 내적 결과를 알아야 하는데 아래에 그 결과가 주어져 있다.
$\hat{i}\cdot\hat{i}=\hat{j}\cdot\hat{j}=\hat{k}\cdot\hat{k}=1\cdot1\cdot\cos 0^\circ=1$
$\hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{k}=\hat{k}\cdot\hat{i}=1\cdot1\cdot\cos 90^\circ=0$
$\hat{j}\cdot\hat{i}=\hat{k}\cdot\hat{j}=\hat{i}\cdot\hat{k}=1\cdot1\cdot\cos 90^\circ=0$
위 결과를 이용하면, \begin{eqnarray} \vec{A}\cdot\vec{B}&=&A_xB_x\hat{i}\cdot\hat{i}+A_xB_y\hat{i}\cdot\hat{j}+A_xB_z\hat{i}\cdot\hat{k} \nonumber\\ &+&A_yB_x\hat{j}\cdot\hat{i}+A_yB_y\hat{j}\cdot\hat{j}+A_yB_z\hat{j}\cdot\hat{k} \nonumber\\ &+&A_zB_x\hat{k}\cdot\hat{i}+A_zB_y\hat{k}\cdot\hat{j}+A_zB_z\hat{k}\cdot\hat{k} \nonumber\\ &=&A_xB_x+A_yB_y+A_zB_z\nonumber \end{eqnarray} 참고로 만약 같은 벡터끼리 내적을 하면 크기의 제곱이 얻어진다.
$\vec{A}\cdot\vec{A}=A_x^2+A_y^2+A_z^2=A^2$

예제
그림과 같이 $\vec{A}$, $\vec{B}$, $\vec{C}$ 세 벡터가 $\vec{C}=\vec{A}+\vec{B}$을 만족한다. $\vec{C}$의 크기를 $\vec{A}$와 $\vec{B}$의 크기와 그 사이각 $\phi$로 표시하라.
풀이
$\vec{C}=\vec{A}+\vec{B}$ 이 식의 양변을 내적으로 제곱해보자. \begin{eqnarray} \vec{C}\cdot\vec{C}&=&(\vec{A}+\vec{B})\cdot(\vec{A}+\vec{B})\nonumber\\ C^2&=&\vec{A}\cdot\vec{A}+\vec{A}\cdot\vec{B}+\vec{B}\cdot\vec{A}+\vec{B}\cdot\vec{B}\nonumber\\ &=&A^2+B^2+2AB\cos\phi \end{eqnarray} 그러므로 $C=\sqrt{A^2+B^2+2AB\cos\phi}$.
$\vec{A}$와 $\vec{B}$ 벡터 사이각 $\phi$는 다음과 같이 얻어질 수 있다. $$ \cos\phi = \frac{C^2-A^2-B^2}{2 A B} $$ $$ \phi = \cos^{-1} \left( \frac{C^2-A^2-B^2}{2 A B} \right) $$

• vector의 곱셉2(외적)


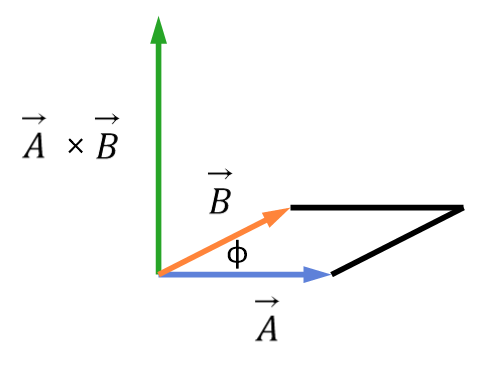
그림 1-14
외적은 곱셈의 결과가 벡터이기 때문에 벡터곱이라고도 불린다. $\vec{A}$와 $\vec{B}$의 외적은 $\vec{A}\times\vec{B}$로 표시하고, A cross B 라고 읽는다.
외적의 정의
$\vec{A}\times\vec{B}$의 크기는 $AB\sin\phi$인데 이것은 그림 x에서 보는 바와 같이 $\vec{A}$와 $\vec{B}$가 이루는 평행사변형의 면적이다.
$\vec{A}\times\vec{B}$의 방향은 오른손 좌표계에서 $xy$ 평면에 $z$축을 추가할때와 비슷한 방법으로 정해진다.
즉, $\vec{A}\times\vec{B}$의 방향은 $\vec{A}$와 $\vec{B}$가 이루는 평면에 수직한 방향인데, 그 면에 수직한 두 방향중에, $\vec{A}$에서 $\vec{B}$로 오른손을 감아쥘 때 엄지손가락이 향하는 수직 방향이다. 이것은 오른손 법칙으로 알려져 있다. 외적은 내적과 달리 교환법칙이 성립하지 않는다. 그림과 같이, $\vec{A}\times\vec{B}$와 $\vec{B}\times\vec{A}$는 크기는 같으나, 반대 방향이라는 것을 알 수 있다.
$\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}$
외적의 성분표시
$\vec{A}$와 $\vec{B}$ 두 벡터가 다음과 같이 성분으로 표시될 때 외적을 계산해보자.
$\vec{A}=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}$,
$\vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k}$
$\vec{A}\times\vec{B}$
$=(A_x \hat{i}+A_y \hat{j}+A_z \hat{k})\times(B_x \hat{i}+B_y \hat{j}+B_z \hat{k})$
이 연산을 하기 위해서는 단위벡터들 사이의 외적 결과를 알아야 하는데, 아래에 그 결과가 주어져 있다.
$\hat{i}\times\hat{i}=\hat{j}\times\hat{j}=\hat{k}\times\hat{k}=1\cdot1\cdot\sin 0^\circ=0$
$\hat{i}\times\hat{j}=\hat{k}$, $\hat{j}\times\hat{k}=\hat{i}$, $\hat{k}\times\hat{i}=\hat{j}$
$\hat{j}\times\hat{i}=-\hat{k}$, $\hat{k}\times\hat{j}=-\hat{i}$, $\hat{i}\times\hat{k}=-\hat{j}$
이 결과를 이용하면 \begin{eqnarray} \vec{A}\times\vec{B}&=&A_xB_x\hat{i}\times\hat{i}+A_xB_y\hat{i}\times\hat{j}+A_xB_z\hat{i}\times\hat{k} \nonumber\\ &+&A_yB_x\hat{j}\times\hat{i}+A_yB_y\hat{j}\times\hat{j}+A_yB_z\hat{j}\times\hat{k} \nonumber\\ &+&A_zB_x\hat{k}\times\hat{i}+A_zB_y\hat{k}\times\hat{j}+A_zB_z\hat{k}\times\hat{k} \nonumber\\ &=&(A_yB_z-A_zB_y)\hat{i}+(A_zB_x-A_xB_z)\hat{j}+(A_xB_y-A_yB_x)\nonumber\\ \end{eqnarray} 위 결과는 다음과 같이 쓸수도 있다. \begin{eqnarray} \vec{A}\times\vec{B}&=&\left|\begin{array}{cc} A_y & A_z \\ B_y & B_z \end{array}\right|\hat{i}+ \left|\begin{array}{cc} A_z & A_x \\ B_z & B_x \end{array}\right|\hat{j}+ \left|\begin{array}{cc} A_x & A_y \\ B_x & B_y \end{array}\right|\hat{k}\nonumber\\ &=&\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{array}\right| \end{eqnarray} 벡터는 분배법칙이 성립한다는 것이 기하학적인 방법과, 성분 표시법으로 증명이 가능하다.
$c(\vec{A}+\vec{B})=c\vec{A}+c\vec{B}$
$\vec{C}\cdot(\vec{A}+\vec{B})=\vec{C}\cdot\vec{A}+\vec{C}\cdot\vec{B}$
$\vec{C}\times(\vec{A}+\vec{B})=\vec{C}\times\vec{A}+\vec{C}\times\vec{B}$
$c(\vec{A}+\vec{B})$
$=(cA_x+cB_x)\hat{i}+(cA_y+cB_y)\hat{j}$
$=cA_x\hat{i}+ cA_y\hat{j}+cB_x\hat{i}+ cB_y\hat{j}=c\vec{A}+c\vec{B}$
$\vec{C}\cdot(\vec{A}+\vec{B})=\vec{C}\cdot\vec{A}+\vec{C}\cdot\vec{B}$
$\vec{C}\times(\vec{A}+\vec{B})=\vec{C}\times\vec{A}+\vec{C}\times\vec{B}$

• 세벡터의 곱
그림과 같이 $\vec{A} \cdot \vec{B} \times \vec{C} $의 연산 결과는 세 벡터가 형성하는 육면체의 부피이다.

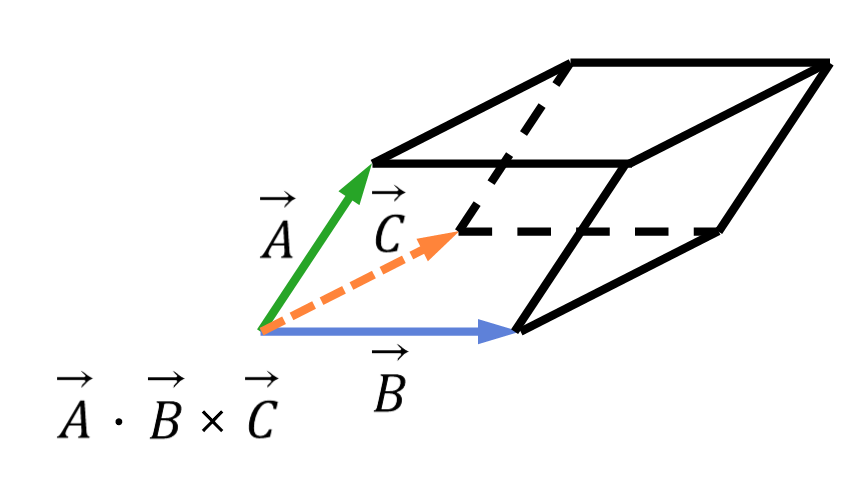
$\vec{A} \cdot \vec{B} \times \vec{C}$는 다음과 같이 계산할 수 있다. $$ \vec{A} \cdot \vec{B} \times \vec{C}=\left|\begin{array}{lll} A_x & A_y & A_z \\ B_x & B_y & B_z \\ C_x & C_y & C_z \end{array}\right|=-\vec{B} \cdot \vec{A} \times \vec{C} $$ $\vec{A} \times(\vec{B} \times \vec{C})$는 다음과 같이 주어지는데, 아래 관계는 종종 back cap rule이라고 알려져 있다. $$ \vec{D}=\vec{A} \times(\vec{B} \times \vec{C})=\vec{B}(\vec{A} \cdot \vec{C})-\vec{C}(\vec{A} \cdot \vec{B}) $$

• vector의 나눗셈

1.2.3 Vector의 미분

• vector 미분 연산자. 델(del) $$ \nabla=\hat{i} \frac{\partial}{\partial x}+\hat{j} \frac{\partial}{\partial y}+\hat{k} \frac{\partial}{\partial z} $$

• Gradient $$ \begin{aligned} \operatorname{grad}= & \nabla \\ & \nabla \varphi=\hat{i} \frac{\partial \varphi}{\partial x}+\hat{j} \frac{\partial \varphi}{\partial y}+\hat{k} \frac{\partial \varphi}{\partial z} \\ & \operatorname{grad} \varphi=\hat{r} \frac{\partial \varphi}{\partial r}+\hat{\theta} \frac{1}{r} \frac{\partial \varphi}{\partial \theta}+\hat{\phi} \frac{1}{r \sin \theta} \frac{\partial \varphi}{\partial \phi} \end{aligned} $$

• Divergence 직교 좌표 $$ \begin{aligned} \operatorname{div}= & \nabla \cdot \\ & \nabla \cdot \vec{F}=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z} \\ \end{aligned} $$
원통 좌표 $$ \begin{aligned} \nabla \cdot \vec{F} & =\frac{1}{r} \frac{\partial}{\partial r}\left(r F_r\right)+\frac{1}{r} \frac{\partial}{\partial \theta} F_\theta+\frac{\partial}{\partial z} F_z \\ \end{aligned} $$ 구 좌표 $$ \begin{aligned} \nabla \cdot \vec{F} & =\frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2 F_r\right)+\frac{1}{r \sin \theta} \frac{\partial}{\partial \theta}\left(F_\theta \sin \theta\right)+\frac{1}{r \sin \theta} \frac{\partial F_\phi}{\partial \phi} \\ \end{aligned} $$

• Curl $$ \begin{aligned} \operatorname{curl}= & \nabla \times \\ &\nabla \times \vec{F}= \left|\begin{array}{lll} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{array}\right| \\ &= \hat{i}\left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right) + \hat{j}\left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right) + \hat{k}\left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) \end{aligned} $$

(예제)
$\vec{G}(x,y,z) = z\hat{i} + xy\hat{j} + 8y\hat{k}$ 위와 같은 벡터장 $\vec{G}$가 주어질 때, (1,2,1)에서 $\vec{G}$의 divergence와 curl을 구하라.

(풀이)
divergence
\begin{aligned} \nabla \cdot \vec{G} &= \frac{\partial G_x}{\partial x}+\frac{\partial G_y}{\partial y}+\frac{\partial G_z}{\partial z} \\ &= \frac{\partial z}{\partial x}+\frac{\partial (xy)}{\partial y}+\frac{\partial (8y)}{\partial z} \\ &= x \\ \end{aligned} 그러므로 (1,2,1)에서 $\vec{G}$의 divergence는 1이다.

curl
\begin{aligned} & \nabla \times \vec{G}= \left|\begin{array}{lll} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ G_x & G_y & G_z \end{array}\right| \\ &= \hat{i}\left(\frac{\partial G_z}{\partial y} - \frac{\partial G_y}{\partial z}\right) + \hat{j}\left(\frac{\partial G_x}{\partial z} - \frac{\partial G_z}{\partial x}\right) + \hat{k}\left(\frac{\partial G_y}{\partial x} - \frac{\partial G_x}{\partial y}\right) \\ & = \hat{i}\left(\frac{\partial (8y)}{\partial y} - \frac{\partial (xy)}{\partial z}\right) + \hat{j}\left(\frac{\partial z }{\partial z} - \frac{\partial (8y)}{\partial x}\right) + \hat{k}\left(\frac{\partial (xy)}{\partial x} - \frac{\partial z}{\partial y}\right) \\ & = \hat{i}\left(8 \right) + \hat{j}\left(1 \right) + \hat{k}\left(y \right) \end{aligned}{ 그러므로 (1,2,1)에서 $\vec{G}$의 curl은 $8\hat{i} + \hat{j} + 2\hat{k}$이다.

• Laplacian
$$ \begin{aligned} \nabla^2 \phi & =\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^2} \frac{\partial^2 \phi}{\partial \theta^2}+\frac{\partial^2 \phi}{\partial z^2} \end{aligned} $$ $$ \begin{aligned} \nabla^2 \phi & =\frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2 \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \phi}{\partial \theta}\right)+\frac{1}{r^2 \sin ^2 \theta} \frac{\partial^2 \phi}{\partial \phi^2} \end{aligned} $$

1.2.4 미분 Vector 항등식들

\begin{equation} \begin{aligned} \nabla \cdot \nabla \varphi & =\nabla^2 \varphi \\ \nabla \cdot \nabla \times \vec{F} & =0 \\ \nabla \times \nabla \varphi & =0 \\ \nabla \times(\nabla \times \vec{F}) & =\nabla(\nabla \cdot \vec{F})-\nabla^2 \vec{F} \\ \nabla(\varphi \psi) & =(\nabla \varphi) \psi+\varphi \nabla \psi \\ \nabla(\vec{F} \cdot \vec{G}) & =(\vec{F} \cdot \nabla) \vec{G}+\vec{F} \times(\nabla \times \vec{G})\\ &+(\vec{G} \cdot \nabla) \vec{F}+\vec{G} \times(\nabla \times \vec{F}) \\ \nabla \cdot(\varphi \vec{F}) & =(\nabla \varphi) \cdot \vec{F}+\varphi \nabla \cdot \vec{F} \\ \nabla \cdot(\vec{F} \times \vec{G}) & =(\nabla \times \vec{F}) \cdot \vec{G}-(\nabla \times \vec{G}) \cdot \vec{F} \\ \nabla \times(\varphi \vec{F}) & =(\nabla \varphi) \times \vec{F}+\varphi \nabla \times \vec{F} \\ \nabla \times(\vec{F} \times \vec{G}) & =(\nabla \cdot \vec{G}) \vec{F}-(\nabla \cdot \vec{F}) \vec{G}+(\vec{G} \cdot \nabla) \vec{F}-(\vec{F} \cdot \nabla) \vec{G} \end{aligned} \end{equation}

1.2.5 Vector의 적분

$\vec{F}=5 t \hat{i}+\hat{j}$로 주어질 때, 벡터 $\vec{A}$를 적분하더라도 다음과 같이 적분변수가 스칼라일 때는 계산이 특별히 더 어렵지는 않다. \begin{eqnarray} \int_0^1 \vec{F} dx= \int_0^1 \left(5 t \hat{i}+\hat{j}\right) dx =\frac{5}{2}\hat{i}+\hat{j} \nonumber \end{eqnarray} 우리가 신경써야할 적분 형태는 적분변수도 벡터인 경우이다.

• vector의 선적분

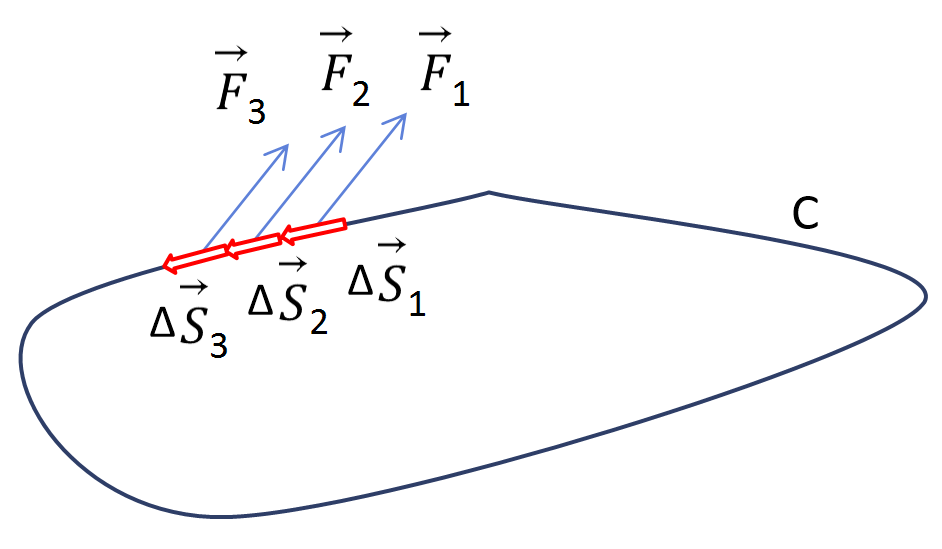
선적분은 경로 적분이라고도 하며, 출발지점에서 종착지점까지 어떤 주어진 경로에 대해서 벡터를 적분을 하는 것이다. 그림,,과 같이 위치 1과 위치 2 사이에 $C$라는 경로가 있고, 경로의 모든 지점에서 벡터 $\vec{F}$가 정의된다고 하자. $\vec{F}$는 공간 좌표의 함수로 주어질 수 도 있다. 경로 $C$를 잘게 $N$개의 조각들로 나누면, 각 조각마다 조각만큼의 길이를 가지며 경로방향을 향하는 미소 경로벡터들 $\Delta\vec{s}_i$을 정의할 수 있다. 아래첨자 $i$는 $i$번째 조각을 의미한다. 그러면 각 조각들에서 벡터 값들 $\vec{F}_i$와 미소 경로벡터들 $\Delta\vec{s}_i$를 내적한 다음에 내적한 양들을 모두 더해준다. \begin{eqnarray} \vec{F}_1\cdot \Delta\vec{s}_1+\vec{F}_2\cdot \Delta\vec{s}_2+\cdots +\vec{F}_N\cdot \Delta\vec{s}_N= \sum_{i=1}^{N} \vec{F}_i\cdot \Delta\vec{s}_i \nonumber \end{eqnarray} 경로를 무한히 잘게 나누면 $N\rightarrow \infty$, $\Delta\vec{s}_i\rightarrow d\vec{s}$, 위 식의 합은 적분이 된다. \begin{eqnarray} \sum_{i=1}^{N} \vec{F}_i\cdot \Delta\vec{s}_i \rightarrow \int_{1,C}^{2} \vec{F}\cdot d\vec{s}\nonumber \end{eqnarray} 이것이 위치1에서 2까지 경로 $C$를 따르는 선적분이다. 이 선적분은 어떤 경로를 택하느냐에 따라 적분값은 당연히 달라질 수 있는데, 만약 적분값이 경로에 무관하게 주어진다면 벡터 $\vec{F}$는 "보존적"이라고 말한다.
때로는 각 조각에서 $\vec{F}_i$와 미소 경로벡터들 $\Delta\vec{s}_i$을 외적을 해서 더하는 경우도 있다. \begin{eqnarray} \int_{1,C}^{2} \vec{F}\times d\vec{s}\quad \textrm{또는}\quad \int_{1,C}^{2} d\vec{s}\times \vec{F} \nonumber \end{eqnarray} 이 적분의 결과는 벡터이다. $$ \begin{aligned} \int_{a, C}^b \nabla \varphi \cdot d \vec{l} & =\int_a^b d \varphi=\left.\varphi\right|_a^b=\varphi_b-\varphi_a \end{aligned} $$

• vector의 면적분

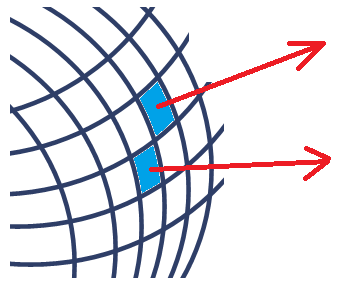
그림,,과 같이 $A$라는 면이 있고, 면의 모든 점에서 벡터 $\vec{F}$가 정의된다고 하자. 면 $A$를 잘게 $N$개의 조각들로 나누면, 각 조각마다 조각만큼의 면적을 가지며 면에 수직한 방향을 향하는 미소 면벡터들 $\Delta\vec{A}_i$을 정의할 수 있다. 그러면 각 조각들에서 벡터 값들 $\vec{F}_i$과 미소 면벡터들 $\Delta\vec{A}_i$를 내적한 다음에 내적한 양들을 모두 더해준다. \begin{eqnarray} \vec{F}_1\cdot \Delta\vec{A}_1+\vec{F}_2\cdot \Delta\vec{A}_2+\cdots +\vec{F}_N\cdot \Delta\vec{A}_N= \sum_{i=1}^{N} \vec{F}_i\cdot \Delta\vec{A}_i \nonumber \end{eqnarray} 면을 무한히 잘게 나누면 $N\rightarrow \infty$, $\Delta\vec{A}_i\rightarrow d\vec{A}$, 위 식의 합은 적분이 된다. \begin{eqnarray} \sum_{i=1}^{N} \vec{F}_i\cdot \Delta\vec{A}_i \rightarrow \int_A \vec{F}\cdot d\vec{A}\nonumber \end{eqnarray}
Stokes 정리
$$ \begin{aligned} \int_S \nabla \times \vec{F} \cdot \hat{n} d a & =\oint_C \vec{F} \cdot d \vec{l} \end{aligned} $$

• vector의 부피적분

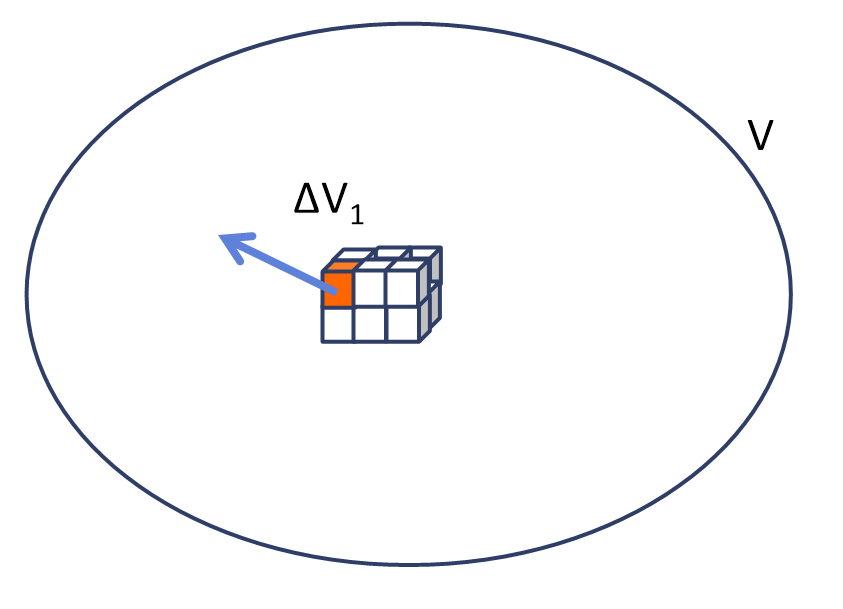
\begin{aligned} \int_V \vec{F} d v \end{aligned} Divergence(발산) 정리
\begin{aligned} \int_V \nabla \cdot \vec{F} d v & =\oint_S \vec{F} \cdot \hat{n} d a \end{aligned}

1.4 복소수

• 복소수의 필요성
다음과 같은 2차방정식의 해는 $$ a z^2+b z+c=0 $$ 다음과 같이 얻어진다. $$ z=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} $$ 위 식에서 $b^2-4 a c$가 음인 경우에 해를 찾기위해서 다음과 같은 특징을 만족하는 기호 $i$를 도입한다. $i=\sqrt{-1}$, $i^2=-1$ 그러면 다음 식들이 성립한다. $$ \sqrt{-16}=4 i, \quad \sqrt{-3}=i \sqrt{3}, \quad i^3=-i $$ $$ \sqrt{-2} \sqrt{-8}=i \sqrt{2} \cdot i \sqrt{8}=-4, \quad i^{4 n}=1 $$ (예제) 다음 2차방정식의 해를 구해보자. $$ z^2-2 z+2=0 $$ 다음과 같이 구해진다. $$ z=\frac{2 \pm \sqrt{4-8}}{2}=\frac{2 \pm \sqrt{-4}}{2}=1 \pm i $$ 위와같이 주어지는 수를 복소수(complex number)라고 부른다.
• 복소수의 실수부와 허수부
복소수는 실수부와 허수부로 이루어져 있다.
$1 \pm i$, $i+5,17 i, 4,3+i \sqrt{5}$
• 복소 평면

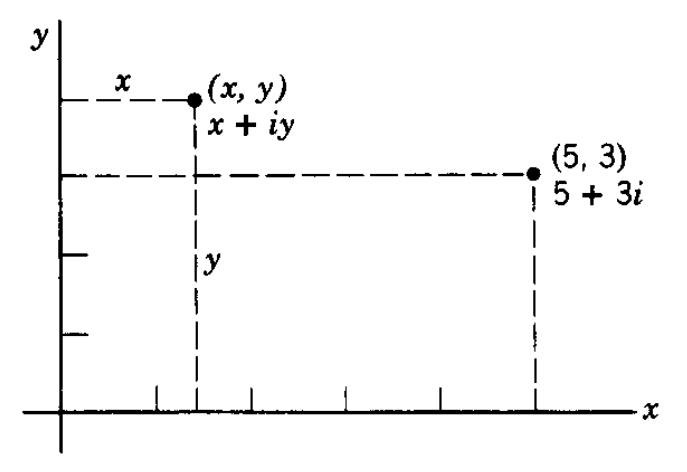
복소수는 그림과 같이 2차원 평면에 하나의 점으로 표시할 수 있다.
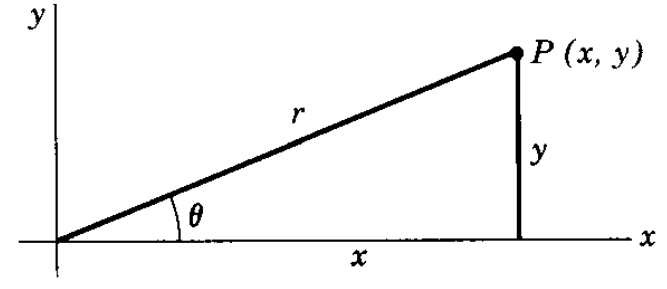
복소수의 실수부와 허수부를 위와 같은 극좌표 형식으로 표시할 수 있다. $$ \begin{aligned} & x=r \cos \theta, \\ & y=r \sin \theta . \end{aligned} $$ 극좌표로 표시된 복소수는 다음과 같이 표기된다. $$ \begin{aligned} x+i y & =r \cos \theta+i r \sin \theta \\ & =r(\cos \theta+i \sin \theta) . \end{aligned} $$ $$ x+i y=r(\cos \theta+i \sin \theta)=r e^{i \theta} . $$ (예제)
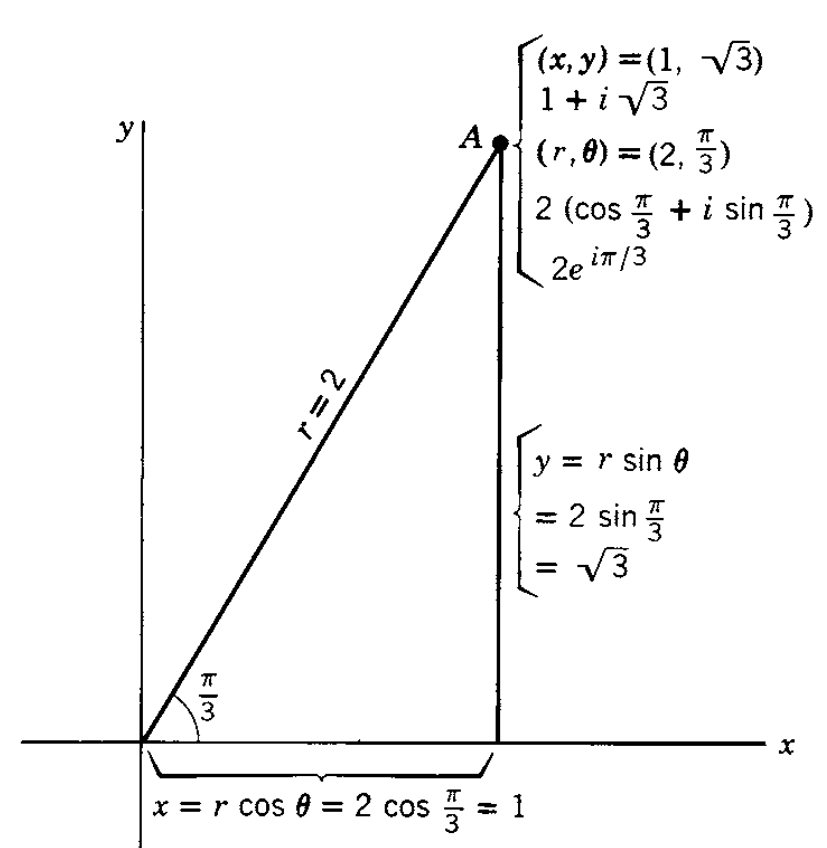
복소수 $1+i \sqrt{3}$는 다음과 같이 표기할 수 있다. $$ 1+i \sqrt{3}=2\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right)=2 e^{i \pi / 3} . $$ • 용어와 표기법
$$ z=x+i y=r(\cos \theta+i \sin \theta)=r e^{i \theta} . $$ 위와 같은 복소수가 있을때, 아래와 같은 표기법이 성립한다. $$ \begin{array}{lll} \operatorname{Re} z=x, & & |z|=\bmod z=r=\sqrt{x^2+y^2} \\ \operatorname{Im} z=y(\text { not } i y), & & \text { angle of } z=\theta \end{array} $$
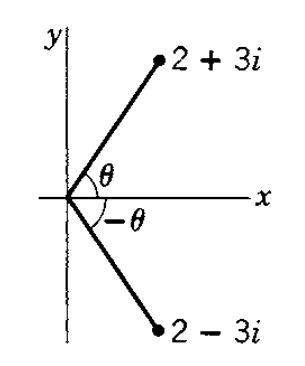
복소 켤레(complex conjugate)는 다음과 같이 정의된다. $$ \bar{z}=r[\cos (-\theta)+i \sin (-\theta)]=r(\cos \theta-i \sin \theta)=r e^{-i \theta} $$

1.5 수열

1.5.1