10. MOSFET의 기초
PN 다이오드 및 Schottky 다이오드는 단일 접합의 2단자 소자로서 전류의 방향에 따른 선택적인 차단 기능을 구현하는 소자이다.
다중 접합의 다중 단자의 소자는 좀더 정교한 기능을 구현할 수 있을 것이다.
이 장에서는 MOSFET(metal-oxide-semiconductor field effect transistor)에 대한 기초적인 물성에 대해서 학습한다.
MOSFET은 이중 접합으로 이루어진 3단자 소자이다.
현대의 컴퓨터 및 스마트폰등에 포함된 CPU등에는 MOSFET이 주로 사용되고 있다.
MOSFET의 세 단자는 각각 source, drain, gate라고 불린다.
10.1 2단자 MOS 구조
MOSFET을 공부하기 전에, MOSFET에 대한 이해를 돕기 위한 준비단계로서 2단자 MOS 구조를 먼저 학습해 보자.
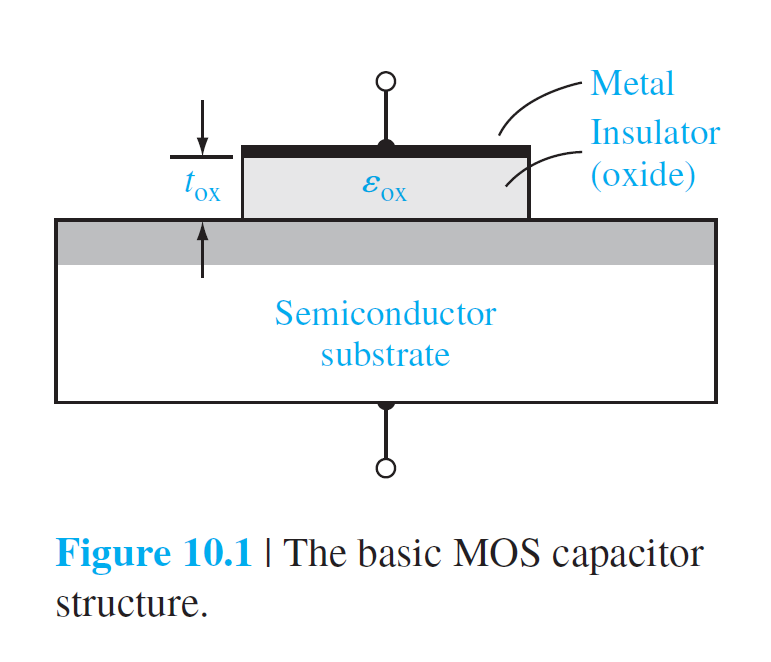
MOS 구조는 그림 10.1에서 보는 바와 같이 금속과 반도체 사이에 산화막이 존재하며, 금속과 반도체에 전압이 가해지는 구조이다.

10.1.1 에너지밴드 다이어그램
MOS 구조를 설명하기위한 유사 구조로서 그림 10.2(a)에 보이는 평행판 축전기 구조를 생각할 수 있다.
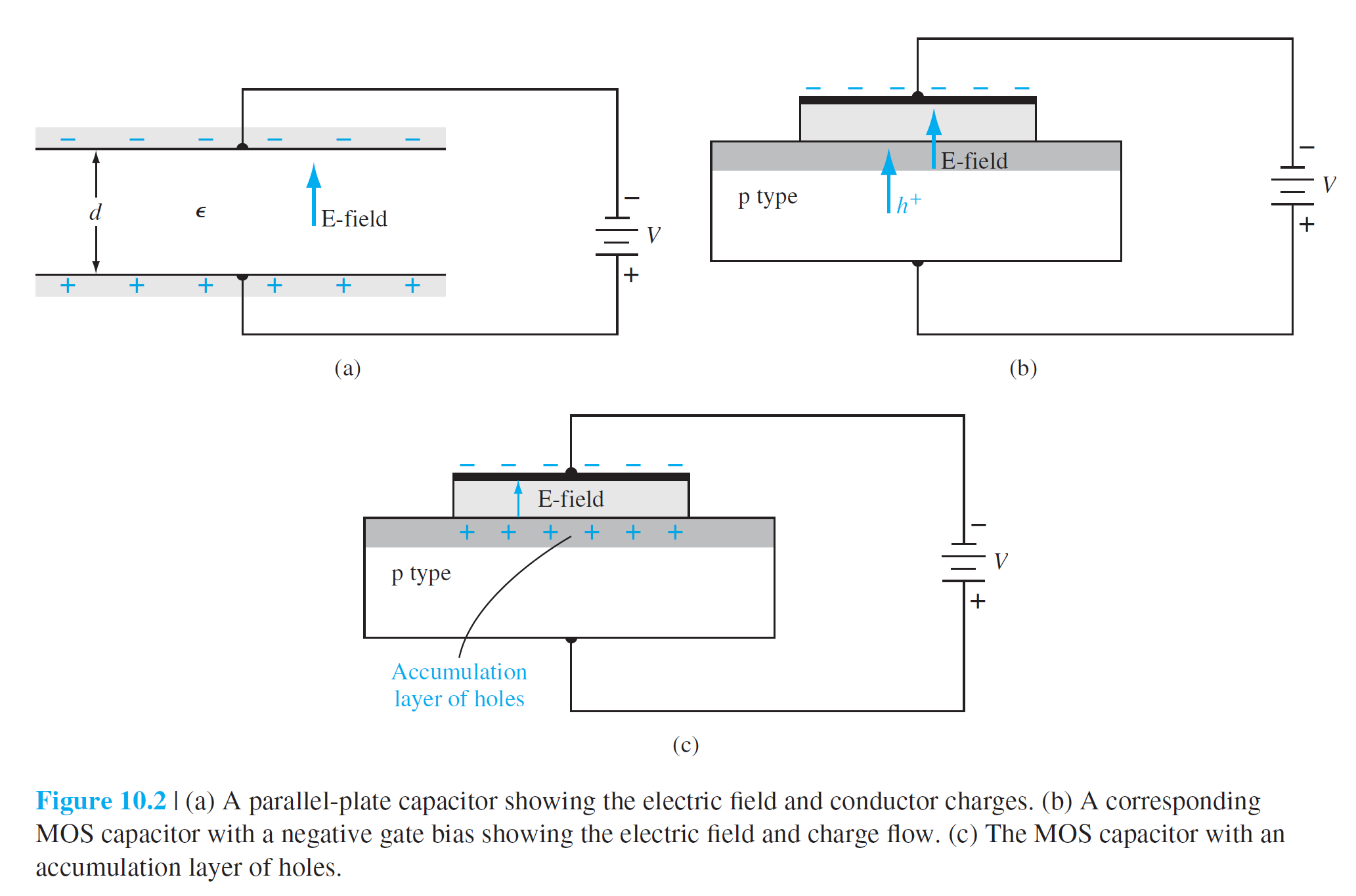
이 축전기의 단위 면적당 전기용량은 다음과 같다. $$ C'=\frac{\epsilon}{d} \qquad (10.1) $$ 이 축전기 양단에 전압 $V$가 가해질 때, 평행판에 대전된 단위 면적당 전하량은 다음과 같다. $$ Q'=C' V \qquad (10.2) $$ 축전기 내부의 전기장은 다음과 같이 주어진다. \begin{equation} E=\frac{V}{d} \qquad (10.3) \end{equation} 그림 10.2(b)는 금속-산화막-반도체(p형) 접합의 MOS 구조를 보여준다. 금속은 MOSFET의 용어에서 gate라고 명명된다. Gate에 음의 포텐셜이 가해지면, 반도체 내에 생성된 전기장에 의하여 다수 운반자인 홀이 산화막-반도체 경계로 쏠리게 된다. 이것을 홀의 축적층(accumulation layer)이라고 한다. 이러한 과정이 그림 10.2(b)와 (c)에 잘 나타나 있다.
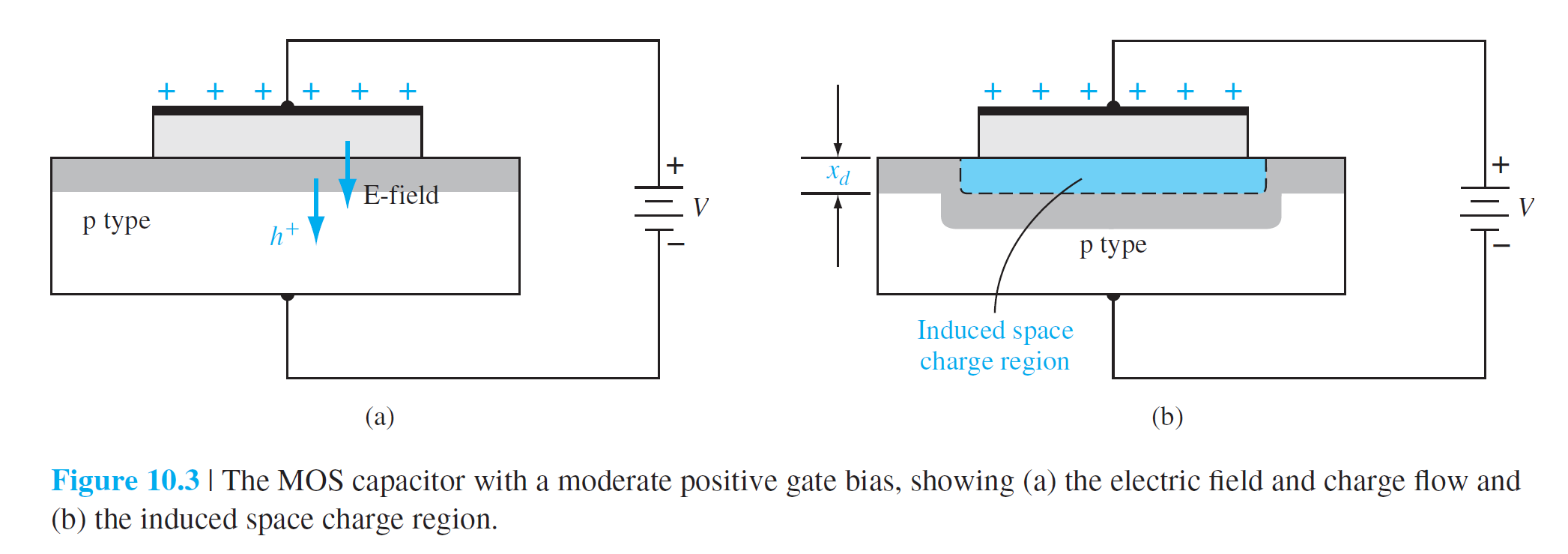
그림 10.3은 그림 2와 동일한 MOS 구조에서 gate에 양의 포텐셜이 가해진 상황을 기술하고 있다. 이 경우에는 반도체 내에 생성된 전기장에 의하여 다수 운반자인 홀이 산화막-반도체 경계에서 멀어지게 되고, 산화막-반도체 경계 부분은 공핍층(음전하)으로 남아 있게 된다.
그림 4는 그림 2와 3에서 언급한 동작에 대응되는 에너지 밴드를 보여주고 있다.
그림 4(a)는 0 전압이 가해질 때의 이상적인 에너지밴드를 보여주고 있는데, 반도체 내의 밴드들은 편평한(flat) 형태를 하고 있다. Flat 밴드의 조건이 형성되면, 반도체의 모든 영역은 중성인 상태가 된다.
그림 4(b)는 gate에 음의 포텐셜이 가해질 때 홀이 산화막-반도체 경계에 축적되는 것을 보여준다. 에너지밴드의 휘어짐은 전자가 경계에서 멀어지는 방향으로 힘을 받는 것을 반영하고 있다. 에너지밴드의 형상에 따라 경계면으로 갈수록 $E_F$는 $E_v$와 가까워 짐을 보여주는데, 이것은 경계 근처의 valence 밴드에 홀의 농도가 크다는 것을 의미한다.
그림 4(c)는 gate에 양의 포텐셜이 가해질 때 홀이 경계에서 멀어지고, 경계 근처에서는 공핍층이 생성되는 것을 보여준다. 에너지밴드의 휘어짐은 전자가 경계쪽으로 힘을 받는 것을 반영하고 있다. 에너지밴드의 형상에 따라 경계면으로 갈수록 $E_F$는 $E_v$와 멀어짐을 보여주는데, 이것은 경계 근처의 valence 밴드에 홀의 농도가 낮다는 것을 의미한다.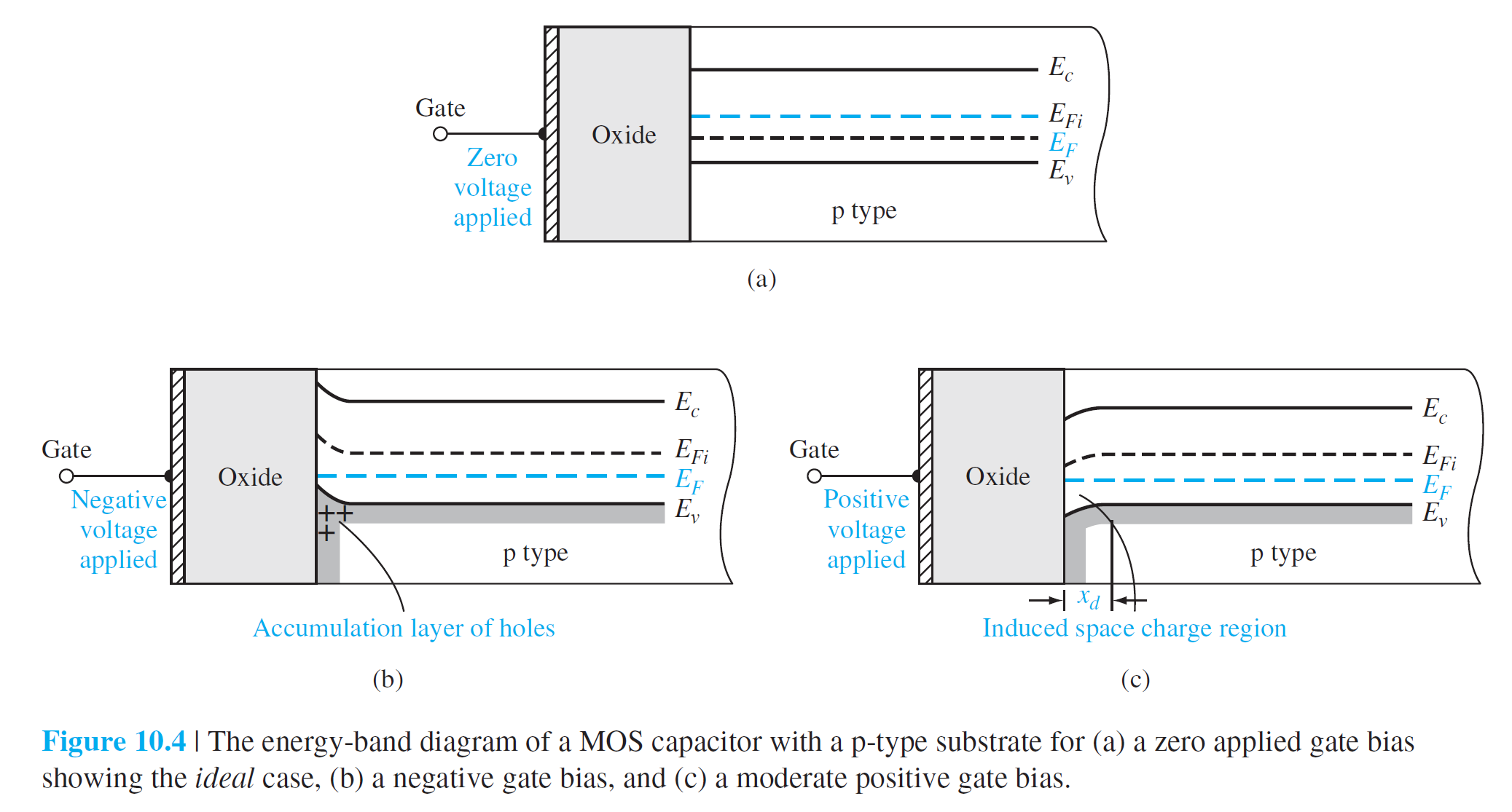
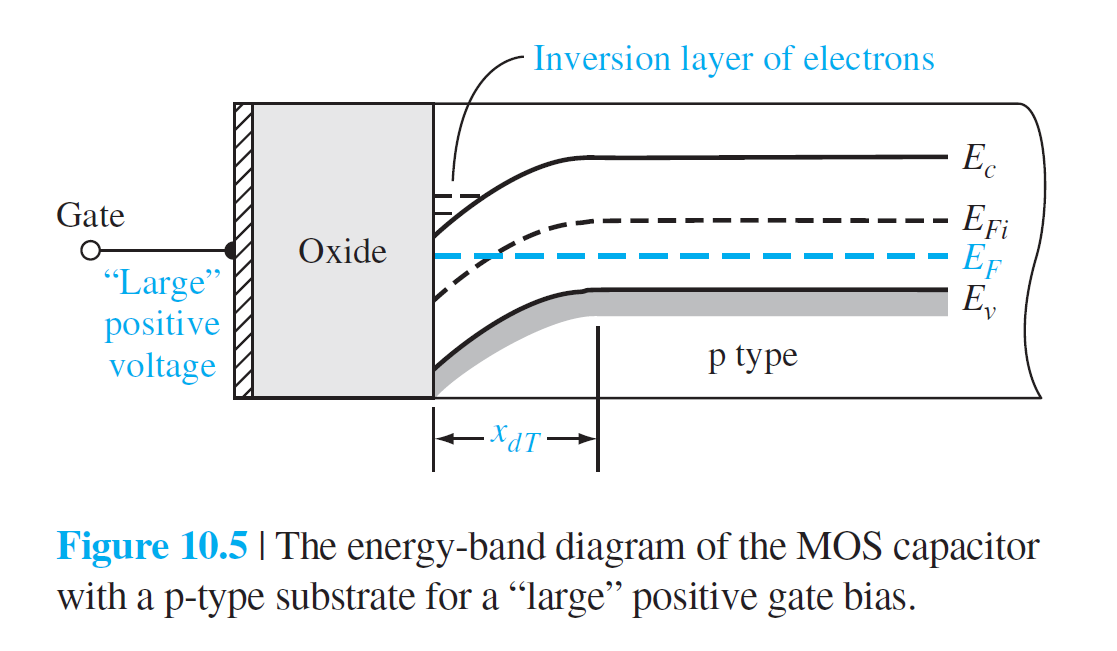
그림 4(c)에서는 경계 근처에서 $E_{F} < E_{Fi}$이기 때문에, 아직은 p형 반도체 상태임을 보여준다. Gate에 좀더 큰 양의 포텐셜을 가하면, 그림 5처럼 $E_{F} > E_{Fi}$이 될수 있다. 이것은 경계 근처가 n형 반도체 특성을 가짐을 의미하고, conduction 밴드에 전자가 채워진다. 이것을 전자의 반전층(inversion layer)이라고 한다.
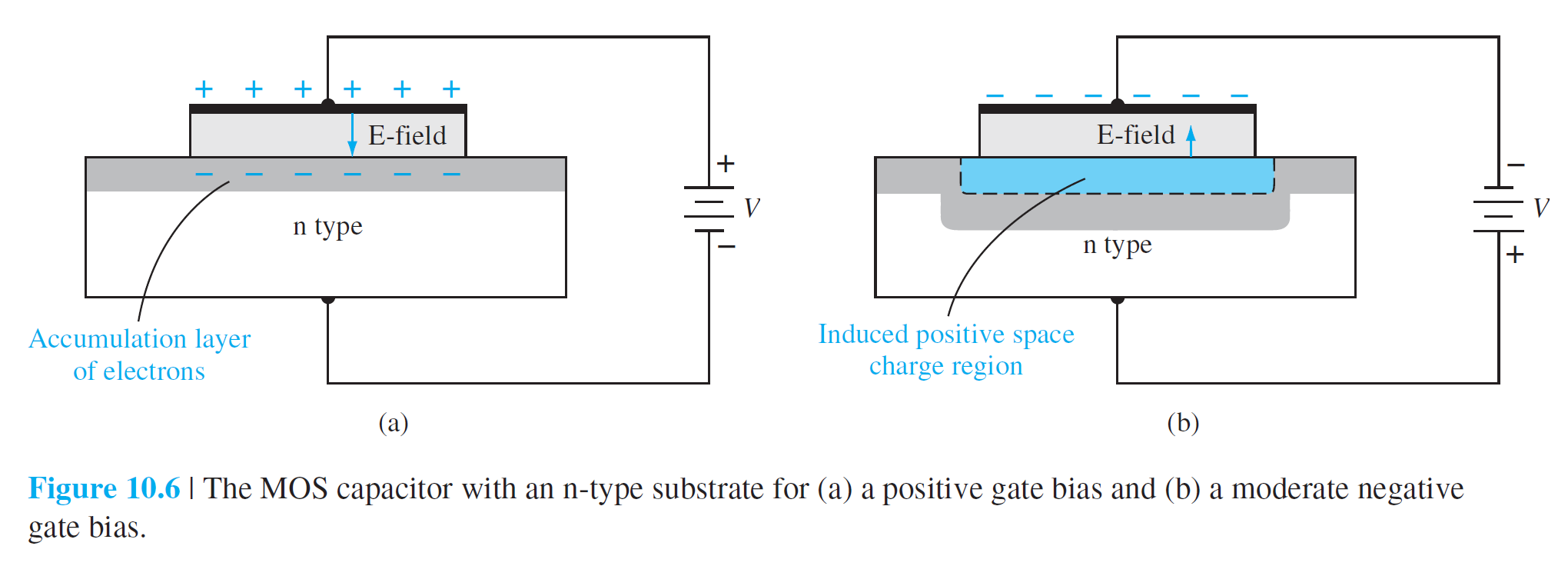
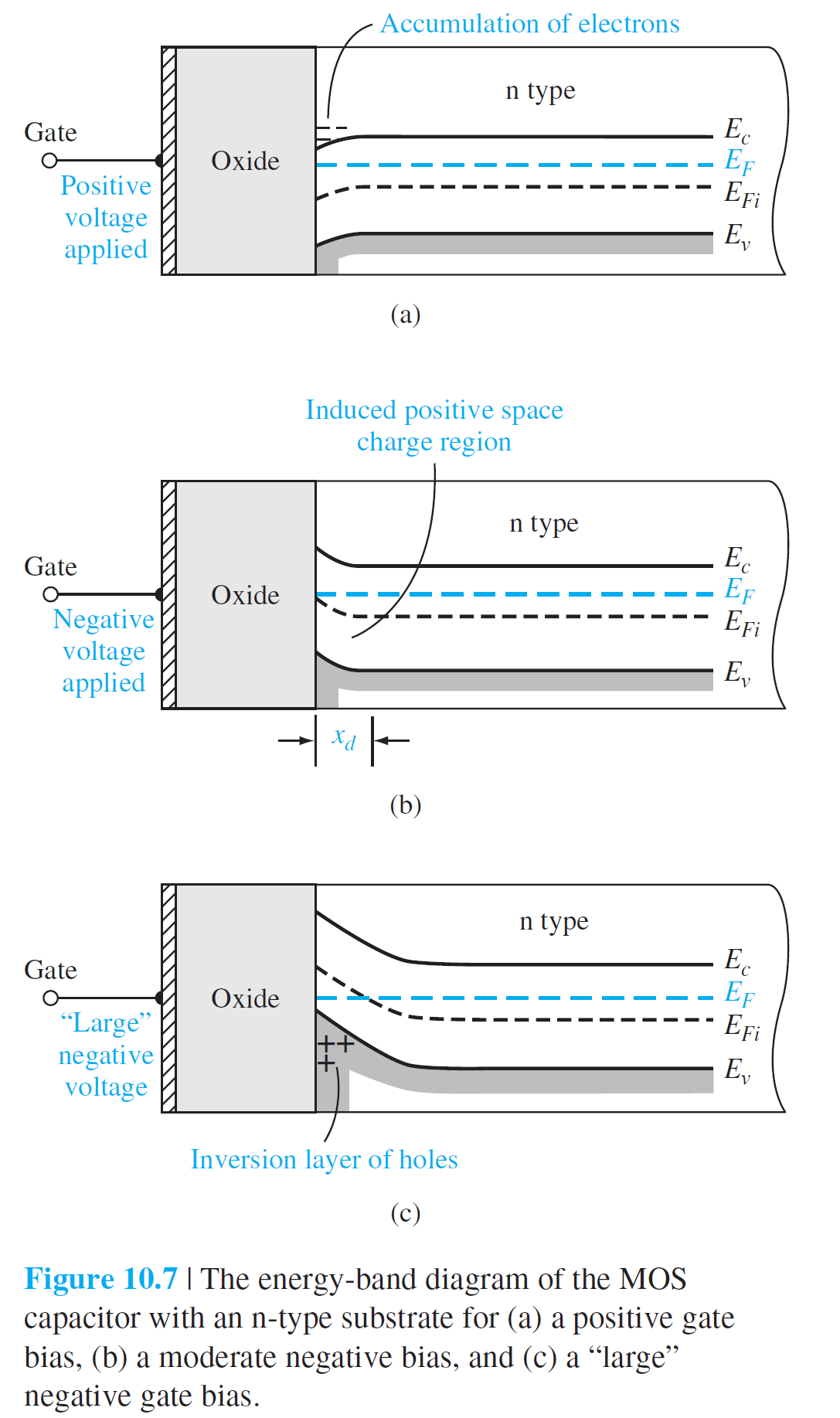
금속-산화막-반도체(n형) MOS 구조는 그림 10.6과 10.7에 설명되어 있다.

이 축전기의 단위 면적당 전기용량은 다음과 같다. $$ C'=\frac{\epsilon}{d} \qquad (10.1) $$ 이 축전기 양단에 전압 $V$가 가해질 때, 평행판에 대전된 단위 면적당 전하량은 다음과 같다. $$ Q'=C' V \qquad (10.2) $$ 축전기 내부의 전기장은 다음과 같이 주어진다. \begin{equation} E=\frac{V}{d} \qquad (10.3) \end{equation} 그림 10.2(b)는 금속-산화막-반도체(p형) 접합의 MOS 구조를 보여준다. 금속은 MOSFET의 용어에서 gate라고 명명된다. Gate에 음의 포텐셜이 가해지면, 반도체 내에 생성된 전기장에 의하여 다수 운반자인 홀이 산화막-반도체 경계로 쏠리게 된다. 이것을 홀의 축적층(accumulation layer)이라고 한다. 이러한 과정이 그림 10.2(b)와 (c)에 잘 나타나 있다.

그림 10.3은 그림 2와 동일한 MOS 구조에서 gate에 양의 포텐셜이 가해진 상황을 기술하고 있다. 이 경우에는 반도체 내에 생성된 전기장에 의하여 다수 운반자인 홀이 산화막-반도체 경계에서 멀어지게 되고, 산화막-반도체 경계 부분은 공핍층(음전하)으로 남아 있게 된다.
그림 4는 그림 2와 3에서 언급한 동작에 대응되는 에너지 밴드를 보여주고 있다.
그림 4(a)는 0 전압이 가해질 때의 이상적인 에너지밴드를 보여주고 있는데, 반도체 내의 밴드들은 편평한(flat) 형태를 하고 있다. Flat 밴드의 조건이 형성되면, 반도체의 모든 영역은 중성인 상태가 된다.
그림 4(b)는 gate에 음의 포텐셜이 가해질 때 홀이 산화막-반도체 경계에 축적되는 것을 보여준다. 에너지밴드의 휘어짐은 전자가 경계에서 멀어지는 방향으로 힘을 받는 것을 반영하고 있다. 에너지밴드의 형상에 따라 경계면으로 갈수록 $E_F$는 $E_v$와 가까워 짐을 보여주는데, 이것은 경계 근처의 valence 밴드에 홀의 농도가 크다는 것을 의미한다.
그림 4(c)는 gate에 양의 포텐셜이 가해질 때 홀이 경계에서 멀어지고, 경계 근처에서는 공핍층이 생성되는 것을 보여준다. 에너지밴드의 휘어짐은 전자가 경계쪽으로 힘을 받는 것을 반영하고 있다. 에너지밴드의 형상에 따라 경계면으로 갈수록 $E_F$는 $E_v$와 멀어짐을 보여주는데, 이것은 경계 근처의 valence 밴드에 홀의 농도가 낮다는 것을 의미한다.

그림 4(c)에서는 경계 근처에서 $E_{F} < E_{Fi}$이기 때문에, 아직은 p형 반도체 상태임을 보여준다. Gate에 좀더 큰 양의 포텐셜을 가하면, 그림 5처럼 $E_{F} > E_{Fi}$이 될수 있다. 이것은 경계 근처가 n형 반도체 특성을 가짐을 의미하고, conduction 밴드에 전자가 채워진다. 이것을 전자의 반전층(inversion layer)이라고 한다.

금속-산화막-반도체(n형) MOS 구조는 그림 10.6과 10.7에 설명되어 있다.


10.1.2 공핍층의 두께
경계 근처에서 반도체에 유도된 공핍층의 폭을 계산해보자.
그림 10.8은 p형 반도체 기판에 생성된 공핍층을 보여주고 있다.
그림에서 $\phi_{Fp}$는 $\phi_{Fp}= \left| E_{Fi} - E_{F} \right|$으로 정의되며, 다음과 같이 주어진다.
\begin{equation}
\phi_{Fp}=V_t \ln \left(\frac{N_a}{n_i}\right) \qquad (10.4)
\end{equation}
여기서 $N_a$는 p형 반도체의 도핑 농도이고, $n_i$는 진성 반도체 농도이다.
표면 포텐셜(surface potnetial) $\phi_s$는 다음과 같이 정의된다.
\begin{equation}
e\phi_s = E_{Fi, 벌크} - E_{Fi, 표면}
\end{equation}
계단식 공핍층 근사를 사용하고 일방 $p^+n$ 접합 다이오드를 참고하면, 공핍층의 폭은 다음과 같이 주어진다.
\begin{equation}
x_d=\sqrt{\frac{2 \epsilon_s \phi_s}{e N_a}} \qquad (10.5)
\end{equation}
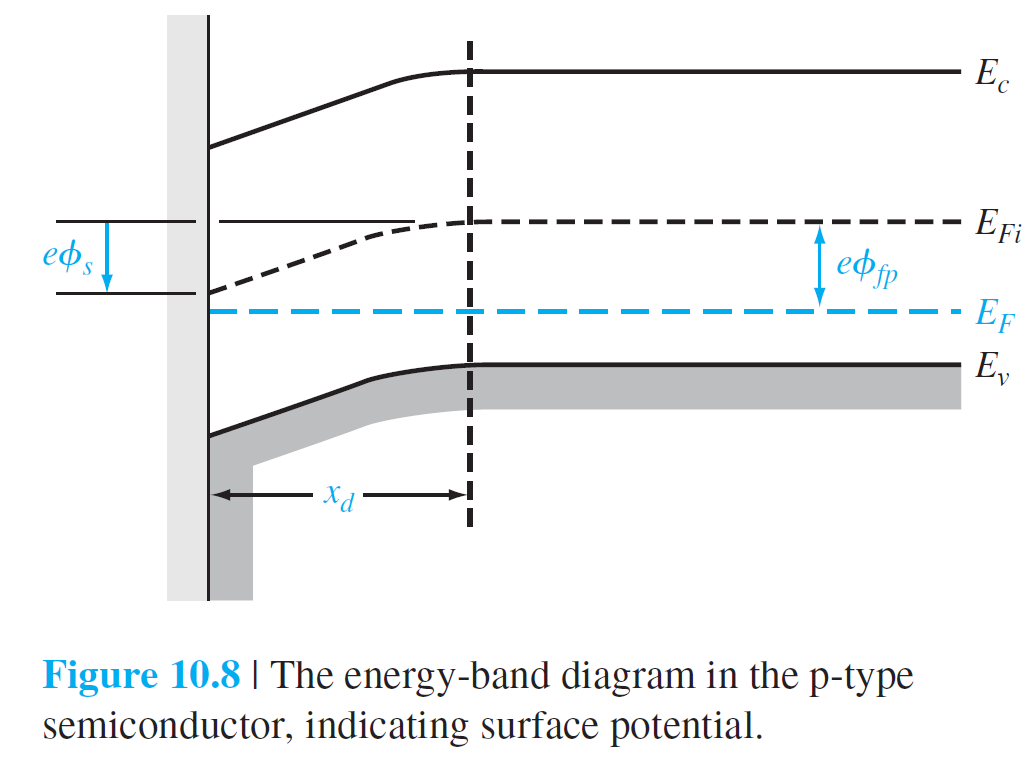
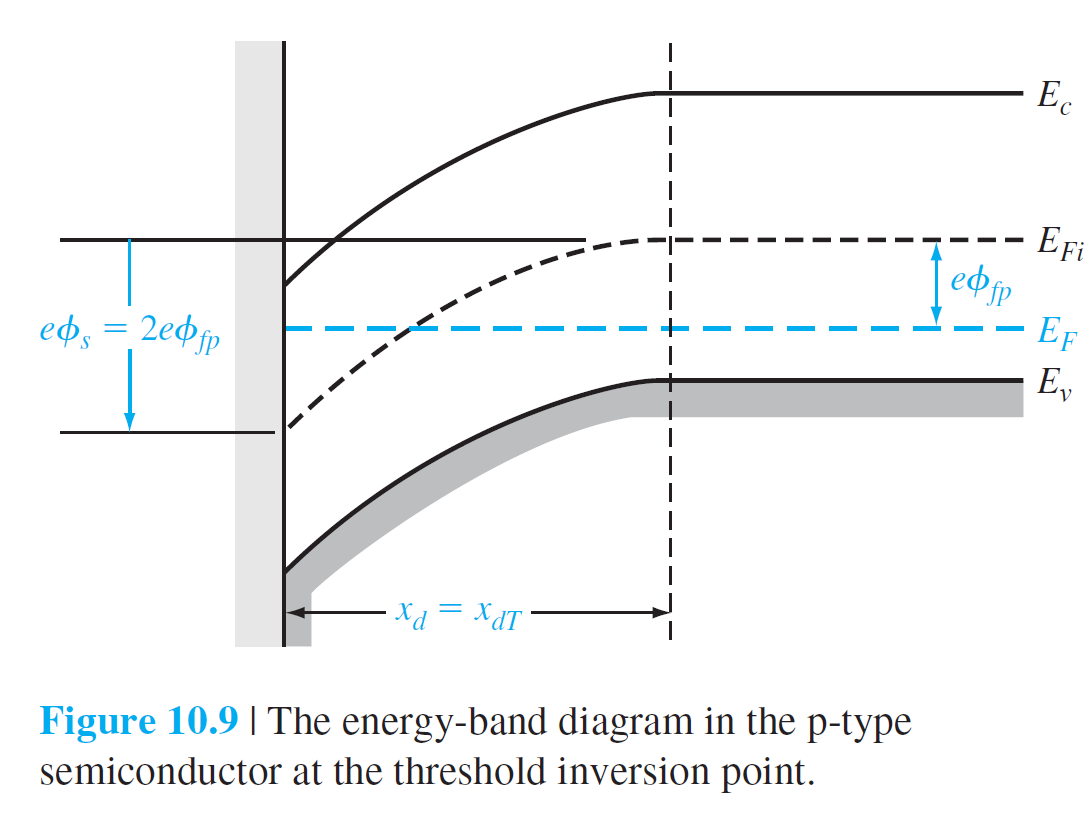
그림 10.9는 $\phi_s=2 \phi_{Fp}$인 경우를 보여준다. 표면에서 $E_F-E_{Fi}$와 벌크 반도체에서 $E_{Fi}-E_F$가 같다는 것을 보여준다. 이것은 표면에서 전자농도와 벌크에서의 홀의 농도가 같다는 것을 의미한다. 이러한 조건을 threshold inversion point(문턱 반전점)이라고 하고, 이때 가해지는 gate 전압($V_G$)을 threshold 전압(문턱 전압, $V_T$)이라고 한다. Threshold inversion point에 도달하면서 conduction 밴드내의 전자들이 풍부해진 상태이기 때문에, $V_G$가 $V_T$를 초과하여 증가하면, 표면에서 $E_F$가 $E_c$에 더 접근 하겠지만, conduction 밴드내의 전자들은 $V_G$에 대해 상대적으로 둔감해진다. Threshold inversion point에서의 공핍층의 폭은 (10.5)식에 $\phi_s = 2 \phi_{Fp}$을 대입하여 다음과 같이 얻어진다. \begin{equation} x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fp}}{e N_a}} \qquad (10.6) \end{equation} n형 반도체 기판에 대해서는 동일한 양들이 다음과 같이 얻어진다. \begin{equation} \begin{aligned} &\phi_{Fn}=V_t \ln \left(\frac{N_d}{n_i}\right) \qquad (10.7) \\[10pt] &x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fn}}{e N_d}} \qquad (10.8) \end{aligned} \end{equation}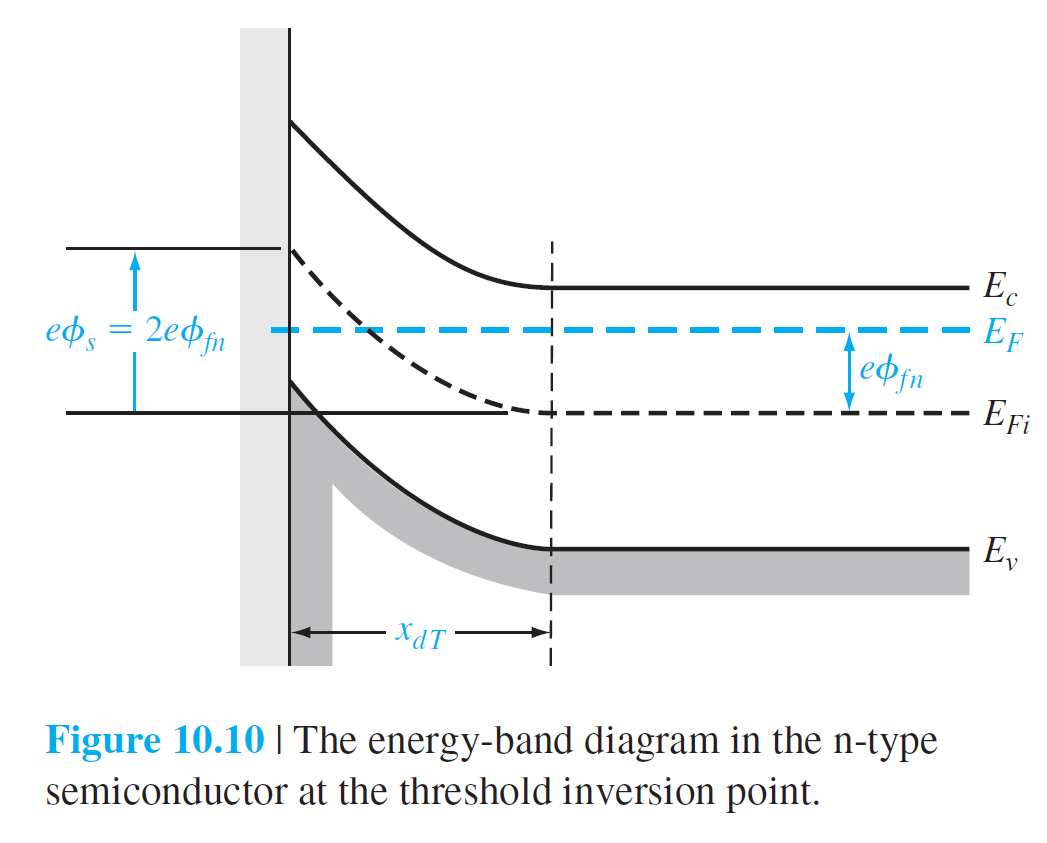
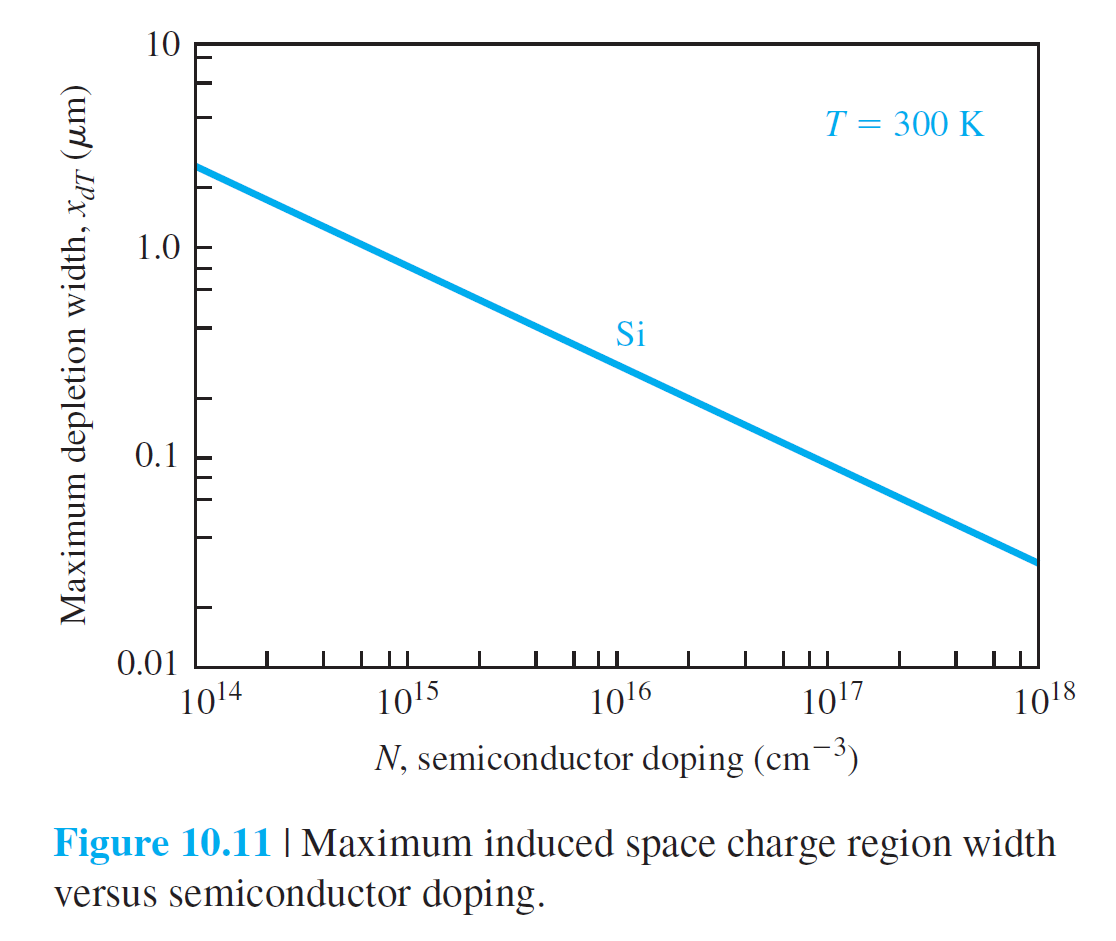



그림 10.9는 $\phi_s=2 \phi_{Fp}$인 경우를 보여준다. 표면에서 $E_F-E_{Fi}$와 벌크 반도체에서 $E_{Fi}-E_F$가 같다는 것을 보여준다. 이것은 표면에서 전자농도와 벌크에서의 홀의 농도가 같다는 것을 의미한다. 이러한 조건을 threshold inversion point(문턱 반전점)이라고 하고, 이때 가해지는 gate 전압($V_G$)을 threshold 전압(문턱 전압, $V_T$)이라고 한다. Threshold inversion point에 도달하면서 conduction 밴드내의 전자들이 풍부해진 상태이기 때문에, $V_G$가 $V_T$를 초과하여 증가하면, 표면에서 $E_F$가 $E_c$에 더 접근 하겠지만, conduction 밴드내의 전자들은 $V_G$에 대해 상대적으로 둔감해진다. Threshold inversion point에서의 공핍층의 폭은 (10.5)식에 $\phi_s = 2 \phi_{Fp}$을 대입하여 다음과 같이 얻어진다. \begin{equation} x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fp}}{e N_a}} \qquad (10.6) \end{equation} n형 반도체 기판에 대해서는 동일한 양들이 다음과 같이 얻어진다. \begin{equation} \begin{aligned} &\phi_{Fn}=V_t \ln \left(\frac{N_d}{n_i}\right) \qquad (10.7) \\[10pt] &x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fn}}{e N_d}} \qquad (10.8) \end{aligned} \end{equation}



10.1.3 표면전하 밀도
(4.39)에 의하면 conduction 밴드의 전자의 농도는 다음과 같이 주어진다.
$$
n=n_i \exp \left[\frac{E_F-E_{Fi}}{kT}\right] \qquad (10.9)
$$
p형 반도체 기판 표면에 생긴 inversion 전자의 농도는 다음과 같이 주어진다.
$$
\begin{aligned}
n_s &= n_i \exp \left[\frac{e\left(\phi_{Fp}+ \phi_s-\phi_{sT} \right)}{kT}\right] \\[10pt]
&= n_i \exp \left[\frac{e\left(\phi_{Fp}+\Delta \phi_s\right)}{kT}\right]=n_i \exp \left[\frac{\phi_{Fp}+\Delta \phi_s}{V_t}\right] \qquad (10.10a) \\[10pt]
&= n_i \exp \left(\frac{\phi_{Fp}}{V_t}\right) \cdot \exp \left(\frac{\Delta \phi_s}{V_t}\right) \qquad (10.10b)
\end{aligned}
$$
$\Delta \phi_s=0$ 이면, threshold inversion 조건이 되므로,
이 조건에서 전자의 농도는 다음과 같다.
$$
n_{sT} = n_i \exp \left(\frac{\phi_{Fp}}{V_t}\right) \qquad (10.11)
$$
그러면 inversion 전자의 농도는 다음과 같이 주어진다.
$$
n_s = n_{sT} \exp \left(\frac{\Delta \phi_s}{V_t}\right) \qquad (10.12)
$$
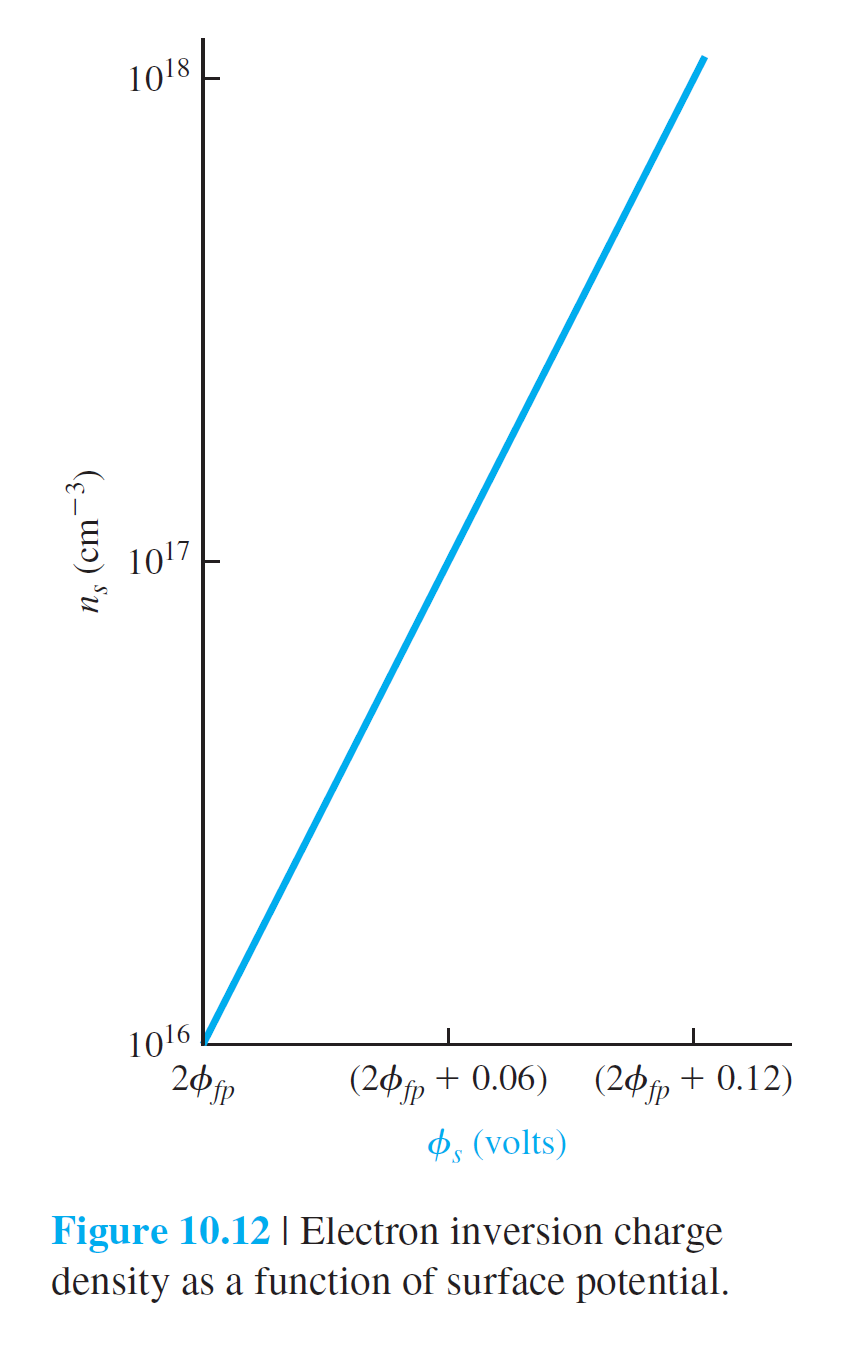
이것은 표면 inversion 전자의 농도($n_s$)가 표면 포텐셜 $\phi_s$에 매우 민감하게 변화한다는 것을 의미한다.
그림 10.12는 $n_{sT} = 10^{16}$ cm$^{-3}$에서 $\phi_s$가 0.06 증가할 때 $n_s$가 10배 증가함을 보여준다.

10.1.4 일함수 차
그림 4(a)는 gate-반도체기판 간의 전압($V_{GB}$)이 0일때 편평한 에너지 밴드를 보여준다.
그러나 실제로는 $V_{GB}=0$ V인 경우에도 종종 에너지 밴드가 편평하지 않게된다.
이것은 크게 두가지 요인에 의해서 발생하게 된다.
하나는 금속의 일함수와 반도체의 일함수가 차이가 날때 이며,
둘째는 경계면들에서 표면전하가 존재하는 경우이다.
이 절에서는 먼저 언급한 일함수 차이에 의한 효과를 알아 본다.
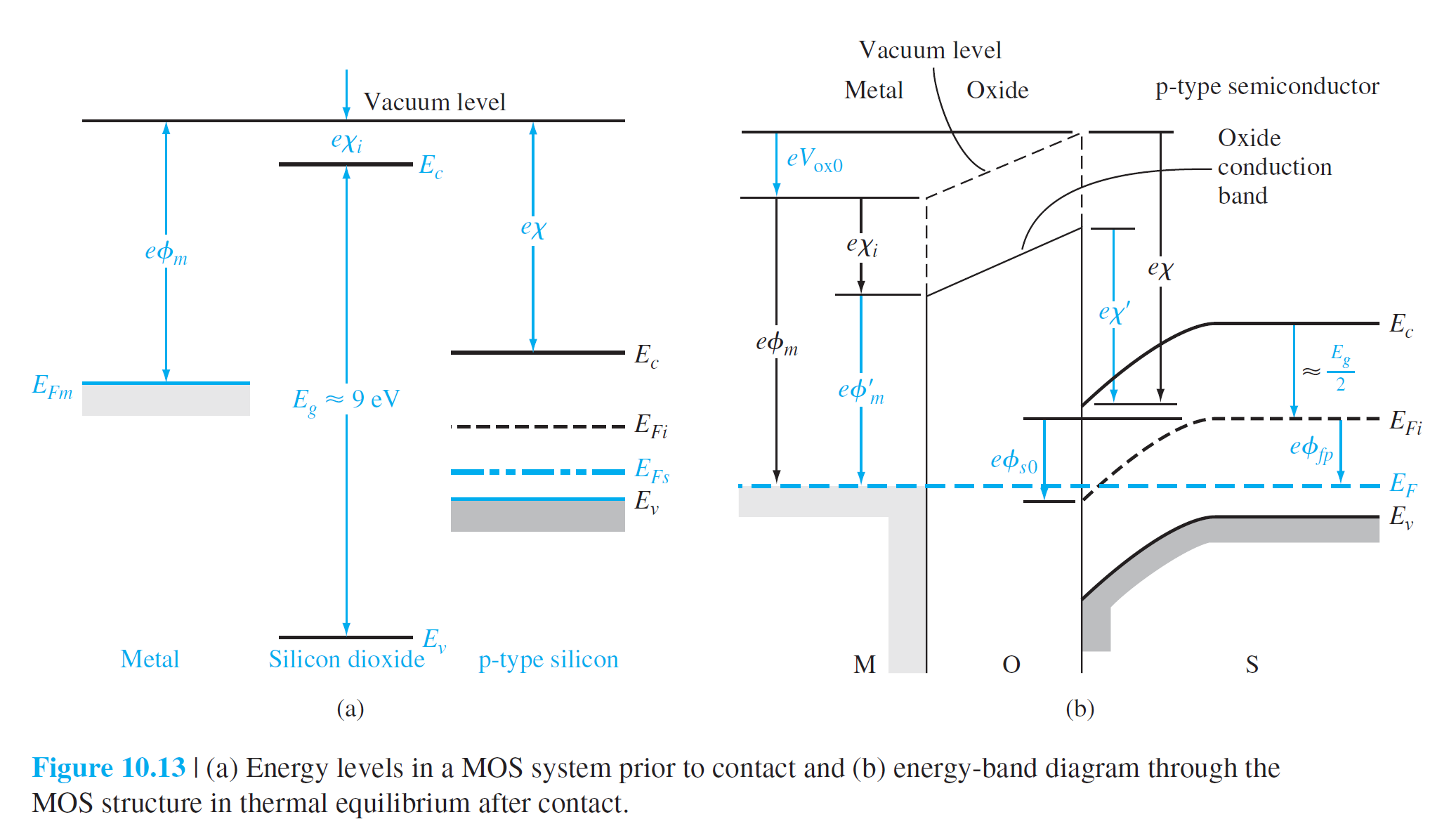
그림 10.13(a)는 진공준위에 대해서 금속, SiO$_2$, Si(p형)에서의 에너지 준위를 보여준다. 그림에 $\chi_i$ 산화막의 전자 친화도인데 SiO$_2$의 경우 $\chi_i=0.9$ V이다.
그림 10.13(b)는 금속-산화물-반도체 접합 후 $V_{GB}=0$일때 에너지 밴드를 보여준다. 전류가 흐르지 않으므로 전체 영역에서 $E_F$는 일정한 값을 가진다. 그림에 나와 있는 기호들에 대해 다음과 같이 정리해보자.
그림 10.13(b)에서 금속 측과 반도체 측에서 $E_F$를 기준으로 에너지를 합하면 다음과 같다.
$$
\begin{aligned}
e \phi_m'+e V_{\mathrm{ox}0} & = e \chi'+\frac{E_g}{2}-e \phi_{s0}+e \phi_{Fp} \qquad (10.13) \\[10pt]
V_{\mathrm{ox}0}+\phi_{s0} & = -\left[\phi_m'-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right] \qquad (10.14)
\end{aligned}
$$
10.13(b)는 $V_{GB}=0$에서도 두 영역에서 포텐셜 하강이 존재한다는 것을 보여주는데,
하나는 산화막 양단 사이의 포텐셜 하락($V_{\mathrm{ox}0}$)이고,
다른 하락은 반도체 공핍층에서의 포텐셜 하락($\phi_{s0}$)이다.
결과적으로 포텐셜 하락의 총합이 식(10.14)에 나타나있고, 이것이 일함수차가 된다.
일함수차를 $\phi_m$로 표기하면 식(10.14)으로 부터 다음과 같이 정의된다.
\begin{equation}
\phi_{ms} \equiv\left[\phi_m'-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right] \qquad (10.15)
\end{equation}

만약 금속-산화물-Si(p형) 접합에서 금속대신 고농도로 도핑된 n형 다결정 Si을 gate로 사용한다면, 그림 10.14(a)와 같은 에너지 다이어그램을 얻는다. 금속대신 고농도로 도핑된 다결정 p형 Si을 gate로 사용한 경우는 그림 10.14(b)에 나타나 있다.
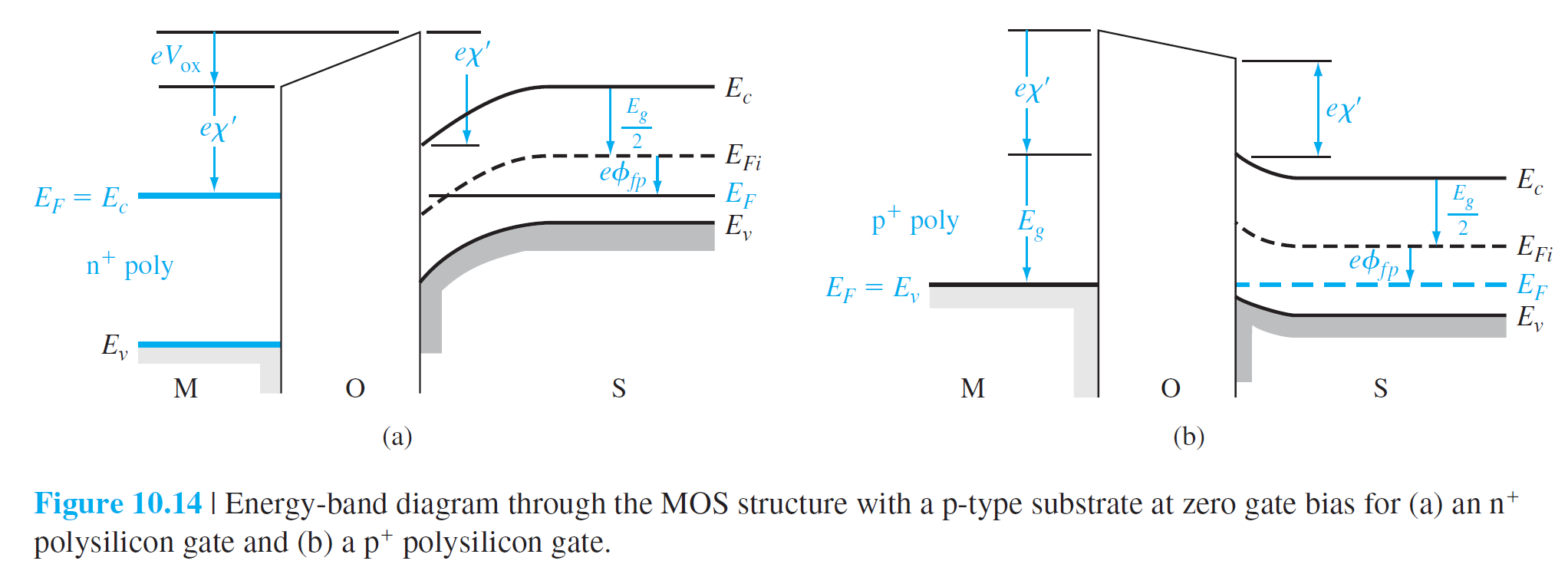
고농도로 도핑된 $n^+$형 다결정 Si에 대해서는 $E_F = E_c$으로, 고농도로 도핑된 $p^+$형 다결정 Si에 대해서는 $E_F = E_v$이라고 가정하자. (그러나 실제로는 고농도로 도핑된 $n^+$ 다결정 Si과 $p^+$ 다결정 Si에 대해 $E_F$는 $E_c$나 $E_v$보다 0.1~0.2 V차이가 있다. ) 그러면 일함수차는 p형 Si기판에 대해서는 다음과 같이 $$ \phi_{ms}=\left[\chi'-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right]=-\left(\frac{E_g}{2 e}+\phi_{Fp}\right) \qquad (10.16) $$ n형 Si기판에 대해서는 다음과 같이 주어진다. $$ \phi_{ms}=\left[\left(\chi'+\frac{E_g}{e}\right)-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right]=\left(\frac{E_g}{2 e}-\phi_{Fp}\right) $$ (10.17) N형 반도체 기판에 대한 에너지 다이어그램과 일함수차는 각각 그림 10.15와 (10.18)식에 나타나 있다. $$ \phi_{ms}=\phi_m'-\left(\chi'+\frac{E_g}{2 e}-\phi_{Fn}\right) \qquad (10.18) $$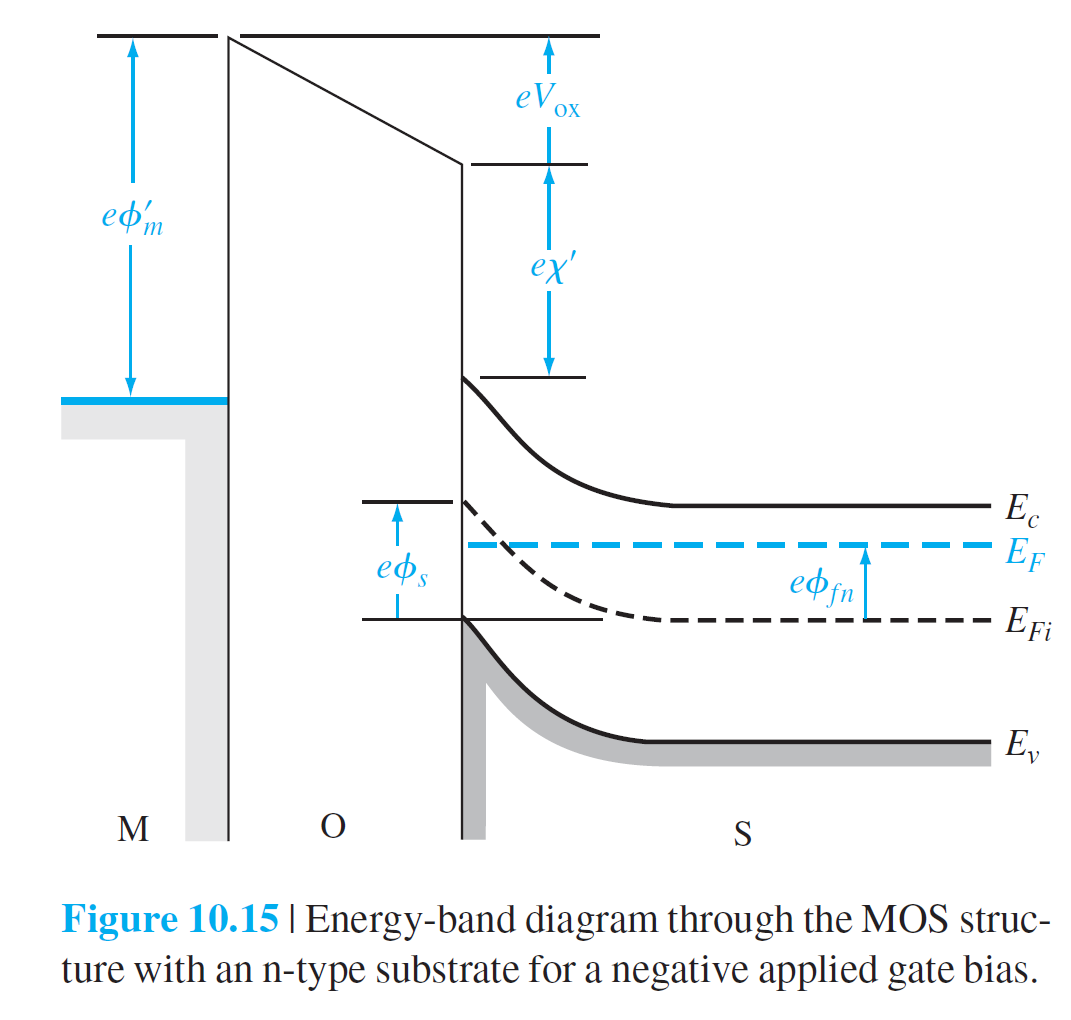
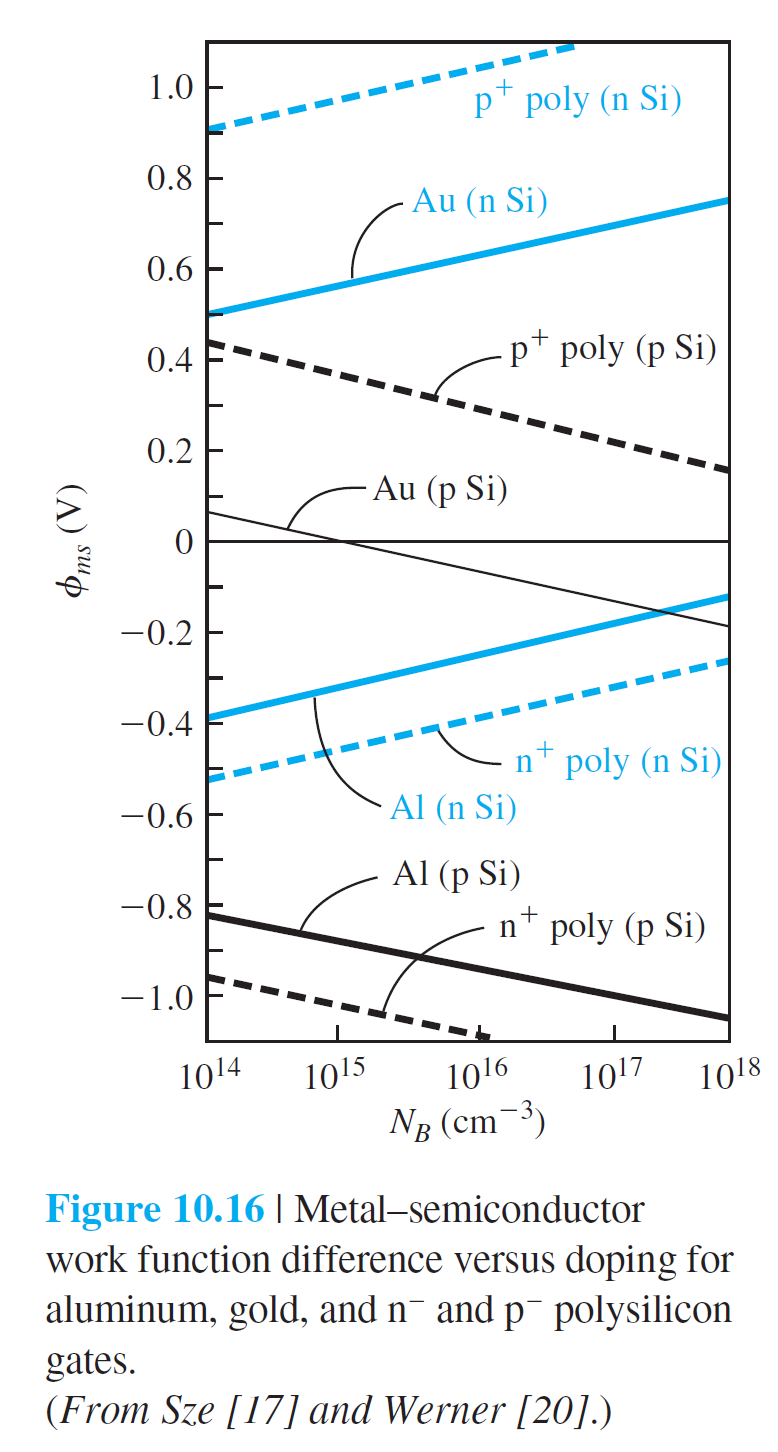
그림 10.16은 다양한 유형의 gate에 대한 일함수차를 보여주고 있다.
이 절에서는 먼저 언급한 일함수 차이에 의한 효과를 알아 본다.

그림 10.13(a)는 진공준위에 대해서 금속, SiO$_2$, Si(p형)에서의 에너지 준위를 보여준다. 그림에 $\chi_i$ 산화막의 전자 친화도인데 SiO$_2$의 경우 $\chi_i=0.9$ V이다.
그림 10.13(b)는 금속-산화물-반도체 접합 후 $V_{GB}=0$일때 에너지 밴드를 보여준다. 전류가 흐르지 않으므로 전체 영역에서 $E_F$는 일정한 값을 가진다. 그림에 나와 있는 기호들에 대해 다음과 같이 정리해보자.
| 기호 | 의미 |
|---|---|
| $\phi_m$ | 금속의 일함수 |
| $\phi_m'$ | 금속의 수정된 일함수 |
| $\chi$ | 반도체의 전자 친화도 |
| $\chi'$ | 반도체의 수정된 전자 친화도 |
| $\chi_i$ | 산화막의 전자 친화도 |
| $V_{\mathrm{ox}0}$ | $V_{GB}=0$ V에 대해 산화막에 양단에 걸리는 전압 |
| $\phi_{s0}$ | 표면 전위 |

만약 금속-산화물-Si(p형) 접합에서 금속대신 고농도로 도핑된 n형 다결정 Si을 gate로 사용한다면, 그림 10.14(a)와 같은 에너지 다이어그램을 얻는다. 금속대신 고농도로 도핑된 다결정 p형 Si을 gate로 사용한 경우는 그림 10.14(b)에 나타나 있다.

고농도로 도핑된 $n^+$형 다결정 Si에 대해서는 $E_F = E_c$으로, 고농도로 도핑된 $p^+$형 다결정 Si에 대해서는 $E_F = E_v$이라고 가정하자. (그러나 실제로는 고농도로 도핑된 $n^+$ 다결정 Si과 $p^+$ 다결정 Si에 대해 $E_F$는 $E_c$나 $E_v$보다 0.1~0.2 V차이가 있다. ) 그러면 일함수차는 p형 Si기판에 대해서는 다음과 같이 $$ \phi_{ms}=\left[\chi'-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right]=-\left(\frac{E_g}{2 e}+\phi_{Fp}\right) \qquad (10.16) $$ n형 Si기판에 대해서는 다음과 같이 주어진다. $$ \phi_{ms}=\left[\left(\chi'+\frac{E_g}{e}\right)-\left(\chi'+\frac{E_g}{2 e}+\phi_{Fp}\right)\right]=\left(\frac{E_g}{2 e}-\phi_{Fp}\right) $$ (10.17) N형 반도체 기판에 대한 에너지 다이어그램과 일함수차는 각각 그림 10.15와 (10.18)식에 나타나 있다. $$ \phi_{ms}=\phi_m'-\left(\chi'+\frac{E_g}{2 e}-\phi_{Fn}\right) \qquad (10.18) $$

그림 10.16은 다양한 유형의 gate에 대한 일함수차를 보여주고 있다.

10.1.5 Flat 밴드 전압
Flat 밴드 전압은 반도체 내에 에너지 밴드의 휘어짐이 없도록 인가된 전압을 의미하고,
이 조건에서는 반도체 내에 공핍층과 공간전하가 존재하지 않는다.
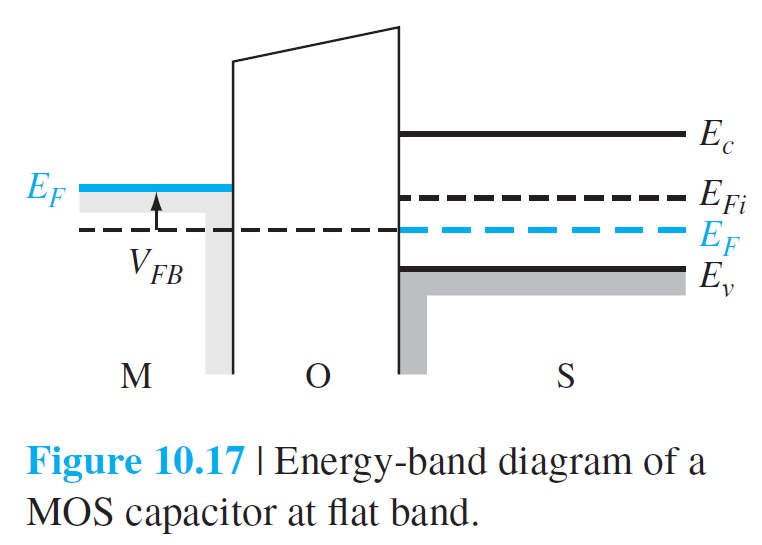
그림 10.17은 flat 밴드가 형성되도록 전압을 걸어준 상태의 에너지 밴드를 보여주고 있다.
10.1.4절에서 언급한 것처럼 그림 10.17은 일함수차와 경계면상에 전하에 의하여
0 전압이 반드시 flat 밴드를 만드는 것이 아님을 보여주고 있다.
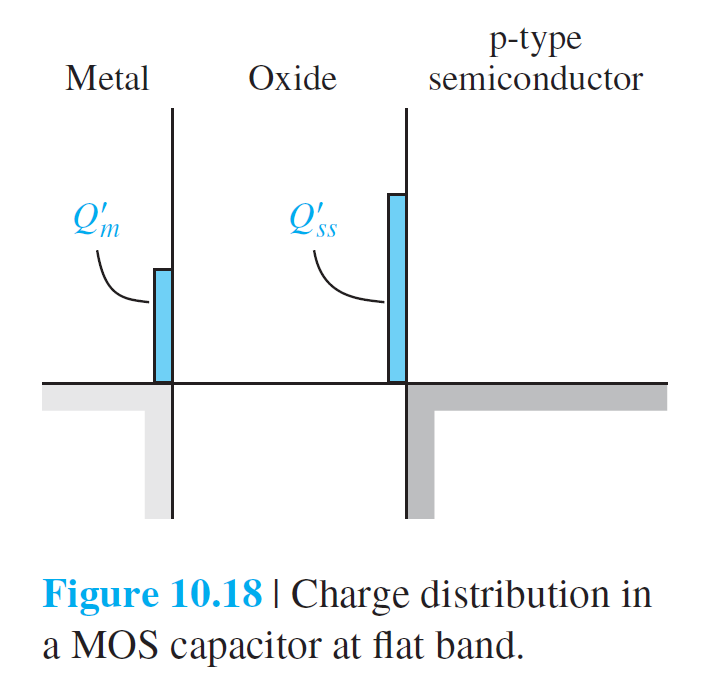
산화물-반도체 접합은 산화물과 반도체를 따로 접합시키기 보다는 Si의 표면을 산화시키는 과정에서 SiO$_2$-Si의 접합이 자연스럽게 형성될 수 있다. 이 경우에 SiO$_2$의 계면에 아직 반응이 되지 않은 Si들에 의한 dangling본드들이 존재할 수 있다. 산화막 처리를 통하여 dangling본드들을 제거 할수있으나 완벽히 제거하지 못한 상태에서 표면 전하가 생성될 수 있다. 그림 10.18은 산화물 내에 존재하는 단위 면적당 표면 전하 $Q_{ss}'$와 그와 반대부호로 금속 표면에 유도된 단위 면적당 전하 $Q_m'$를 보여주고 있다.
$V_{GB}=0$ V에 대해 (10.14)는 다음과 같이 쓸 수 있다. $$ V_{\mathrm{ox}0}+\phi_{s 0}=-\phi_{ms} \qquad (10.19) $$ $V_{GB}\neq 0$에 대해서 $\Delta V_{\mathrm{ox}}$와 $\Delta \phi_s$이 변할 것이다. $$ V_G=\Delta V_{\mathrm{ox}}+\Delta \phi_s=\left(V_{\mathrm{ox}}-V_{\mathrm{ox}0}\right)+\left(\phi_s-\phi_{s 0}\right) \qquad (10.20) $$ 식(10.19)를 이용하면 다음 식을 얻는다. $$ V_G=V_{\mathrm{ox}}+\phi_s+\phi_{ms} \qquad (10.21) $$ 그림 10.18에 전하 중성 조건을 적용하면 다음을 얻는다. $$ Q_m'+Q_{ss}'=0 \qquad (10.22) $$ $V_{\mathrm{ox}}$는 전기용량과 관련이 있어서 다음과 같이 쓸수있다. $$ \begin{aligned} V_{\mathrm{ox}}&=\frac{Q_m'}{C_{\mathrm{ox}}} \qquad (10.23)\\[10pt] &=\frac{-Q_{ss}'}{C_{\mathrm{ox}}} \qquad (10.24) \end{aligned} $$ Flat 밴드 조건에서는 표면 포텐셜($\phi_s$)이 0이므로, 다음이 얻어진다. $$ V_G=V_{FB}=\phi_{ms}-\frac{Q_{ss}'}{C_{\mathrm{ox}}} \qquad (10.25) $$ $V_{FB}$가 flat 밴드 전압이다.


산화물-반도체 접합은 산화물과 반도체를 따로 접합시키기 보다는 Si의 표면을 산화시키는 과정에서 SiO$_2$-Si의 접합이 자연스럽게 형성될 수 있다. 이 경우에 SiO$_2$의 계면에 아직 반응이 되지 않은 Si들에 의한 dangling본드들이 존재할 수 있다. 산화막 처리를 통하여 dangling본드들을 제거 할수있으나 완벽히 제거하지 못한 상태에서 표면 전하가 생성될 수 있다. 그림 10.18은 산화물 내에 존재하는 단위 면적당 표면 전하 $Q_{ss}'$와 그와 반대부호로 금속 표면에 유도된 단위 면적당 전하 $Q_m'$를 보여주고 있다.

$V_{GB}=0$ V에 대해 (10.14)는 다음과 같이 쓸 수 있다. $$ V_{\mathrm{ox}0}+\phi_{s 0}=-\phi_{ms} \qquad (10.19) $$ $V_{GB}\neq 0$에 대해서 $\Delta V_{\mathrm{ox}}$와 $\Delta \phi_s$이 변할 것이다. $$ V_G=\Delta V_{\mathrm{ox}}+\Delta \phi_s=\left(V_{\mathrm{ox}}-V_{\mathrm{ox}0}\right)+\left(\phi_s-\phi_{s 0}\right) \qquad (10.20) $$ 식(10.19)를 이용하면 다음 식을 얻는다. $$ V_G=V_{\mathrm{ox}}+\phi_s+\phi_{ms} \qquad (10.21) $$ 그림 10.18에 전하 중성 조건을 적용하면 다음을 얻는다. $$ Q_m'+Q_{ss}'=0 \qquad (10.22) $$ $V_{\mathrm{ox}}$는 전기용량과 관련이 있어서 다음과 같이 쓸수있다. $$ \begin{aligned} V_{\mathrm{ox}}&=\frac{Q_m'}{C_{\mathrm{ox}}} \qquad (10.23)\\[10pt] &=\frac{-Q_{ss}'}{C_{\mathrm{ox}}} \qquad (10.24) \end{aligned} $$ Flat 밴드 조건에서는 표면 포텐셜($\phi_s$)이 0이므로, 다음이 얻어진다. $$ V_G=V_{FB}=\phi_{ms}-\frac{Q_{ss}'}{C_{\mathrm{ox}}} \qquad (10.25) $$ $V_{FB}$가 flat 밴드 전압이다.

10.1.6 Threshold 전압
Threshold 전압은 threshold inversion 조건을 형성하는 전압으로 그림 10.9에 설명되었다.
이제 표면전하를 추가하여 threshold 전압을 논의해본다.
그림 10.19는 threshold inversion 조건에서 전하 분포를 나타낸다.
공핍층의 폭은 최대가 되고, 금속 표면상에도 이에 대응되는 표면전하량 $Q_{mT}'$이 존재한다.
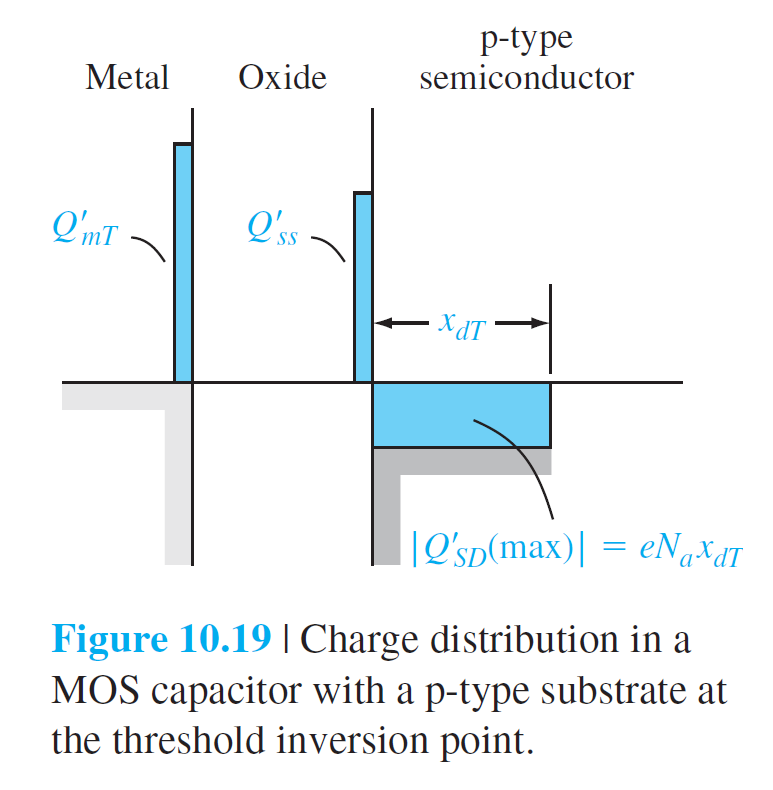
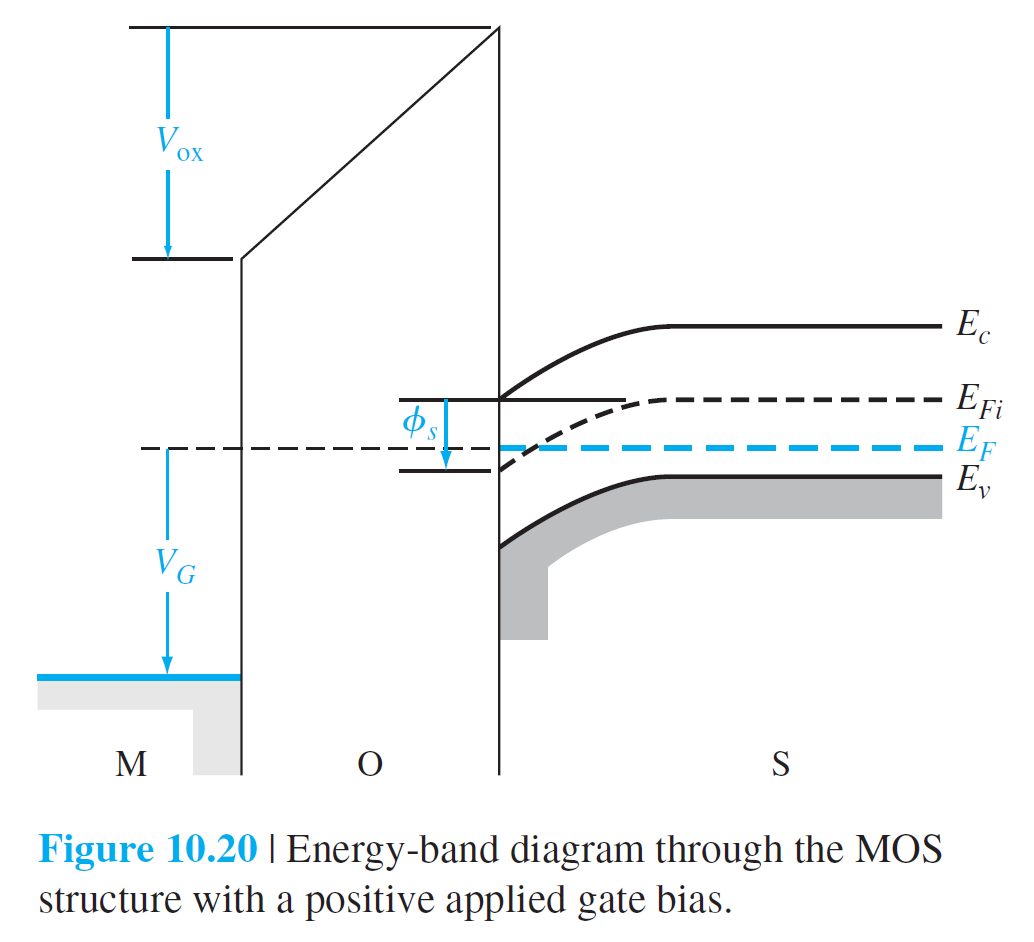
반도체 표면에 inversion 층이 생성되었겠지만, 이를 무시하고, 전하량 보존 법칙을 적용하면, 다음 식을 얻는다. $$ Q_{m T}'+Q_{ss}'=\left|Q_{SD}'(\max )\right| \qquad (10.26) $$ 여기서 $$ \left|Q_{SD}'(\max )\right|=e N_a x_{dT} \qquad (10.27) $$ Gate에 양의 전압을 걸어주면 그림 10.20과 같은 에너지 밴드를 얻는다.
인가된 $V_{GB}$는 $V_{\text {ox }}$와 $\Delta \phi_s$에 변화를 일으킨다. 식 (10.20)과 (10.21)으로부터 다음을 얻는다. $$ V_G=\Delta V_{\text {ox }}+\Delta \phi_s=V_{\text {ox }}+\phi_s+\phi_{ms} $$ Threshold inversion 조건에서 $V_G=V_{TN}$으로 정의하자. $V_{TN}$는 전자 inversion 층을 생기게 하는 threshold 전압이다. 표면 포텐셜 $\phi_s$는 threshold inversion 조건에서 $\phi_s=2 \phi_{Fp}$이므로 다음과 같이 된다. $$ V_{TN}=V_{\text {ox } T}+2 \phi_{Fp}+\phi_{ms} \qquad (10.28) $$ $V_{\mathrm{ox}T}$ threshold inversion 조건에서 $V_{\mathrm{ox}}$이다. $V_{\mathrm{ox}T}$은 전기용량과 관련하여 다음과 같이 주어진다. $$ \begin{aligned} V_{\mathrm{ox}T}&=\frac{Q_{m T}'}{C_{\mathrm{ox}}} \qquad (10.29) \\[10pt] &=\frac{1}{C_{\mathrm{ox}}}\left(\left|Q_{SD}'(\max )\right|-Q_{\mathrm{ss}}'\right) \qquad (10.30) \end{aligned} $$ $C_{\mathrm{ox}}$는 단위 면적당 산화막의 전기용량이다. 결과적으로 threshold 전압은 다음과 같이 주어진다. $$ \begin{aligned} V_{TN}&=\frac{\left|Q_{SD}'(\max )\right|}{C_{\mathrm{ox}}}-\frac{Q_{ss}'}{C_{\mathrm{ox}}}+\phi_{ms}+2 \phi_{Fp} \qquad (10.31a) \\[10pt] &=\left(\left|Q_{SD}'(\max )\right|-Q_{ss}'\right)\left(\frac{t_{\mathrm{ox}}}{\epsilon_{\mathrm{ox}}}\right)+\phi_{ms}+2 \phi_{Fp} \qquad (10.31b) \end{aligned} $$ Flat 밴드 전압에 대한 (10.25)식을 이용하면 다음과 같이 된다. \begin{equation} V_{TN}=\frac{\left|Q_{SD}'(\max )\right|}{C_{\mathrm{ox}}}+V_{FB}+2 \phi_{Fp} \qquad (10.31c) \end{equation} $V_{TN}$는 반도체 도핑, $Q_{ss}'$ 및 산화막 두께 등으로 조절이 가능하다.
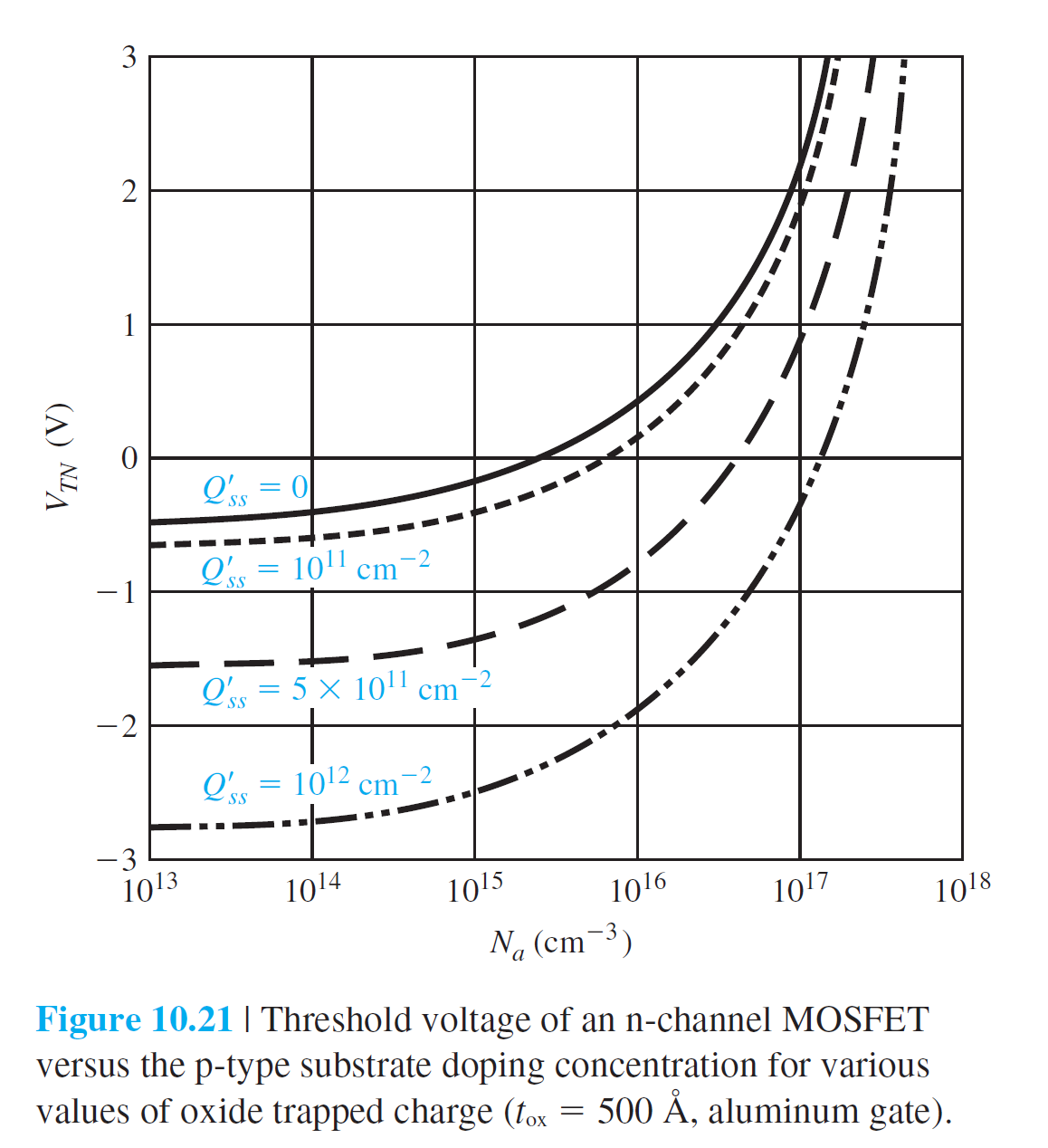
만약 $V_{TN} < 0$ V이라면, $V_G = 0$ V일 때도 inversion 층이 존재함을 의미한다. 이러한 소자를 공핍형 소자임을 의미한다. $V_G = 0$ V일 때 inversion 층이 아직 형성되지 않은 소자를 증가형 소자라고 한다. 그림 10.21은 다양한 산화막 전하값들에 대한 $V_{TN}$-$N_a$ 그래프를 보여주고 있다. 증가형 소자를 얻기 위해서는 p형 반도체가 좀더 높은 도핑이 필요함을 알수있다.
N형 반도체 기판에 대해서는 아래 식들이 유도된다. \begin{equation} \begin{aligned} &V_{T P}=\left(-\left|Q_{SD}'(\max )\right|-Q_{ss}'\right)\left(\frac{t_{\mathrm{ox}}}{\epsilon_{\mathrm{ox}}}\right)+\phi_{ms}-2 \phi_{Fn} \qquad (10.32)\\[10pt] &\begin{gathered} \phi_{ms}=\phi_m'-\left(\chi'+\frac{E_g}{2 e}-\phi_{Fn}\right) \qquad (10.33a)\\[10pt] \left|Q_{SD}'(\max )\right|=e N_d x_{dT} \qquad (10.33b)\\[10pt] x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fn}}{e N_d}} \qquad (10.33c) \end{gathered} \end{aligned} \end{equation} \begin{equation} \phi_{Fn}=V_t \ln \left(\frac{N_d}{n_i}\right) \qquad (10.33d) \end{equation}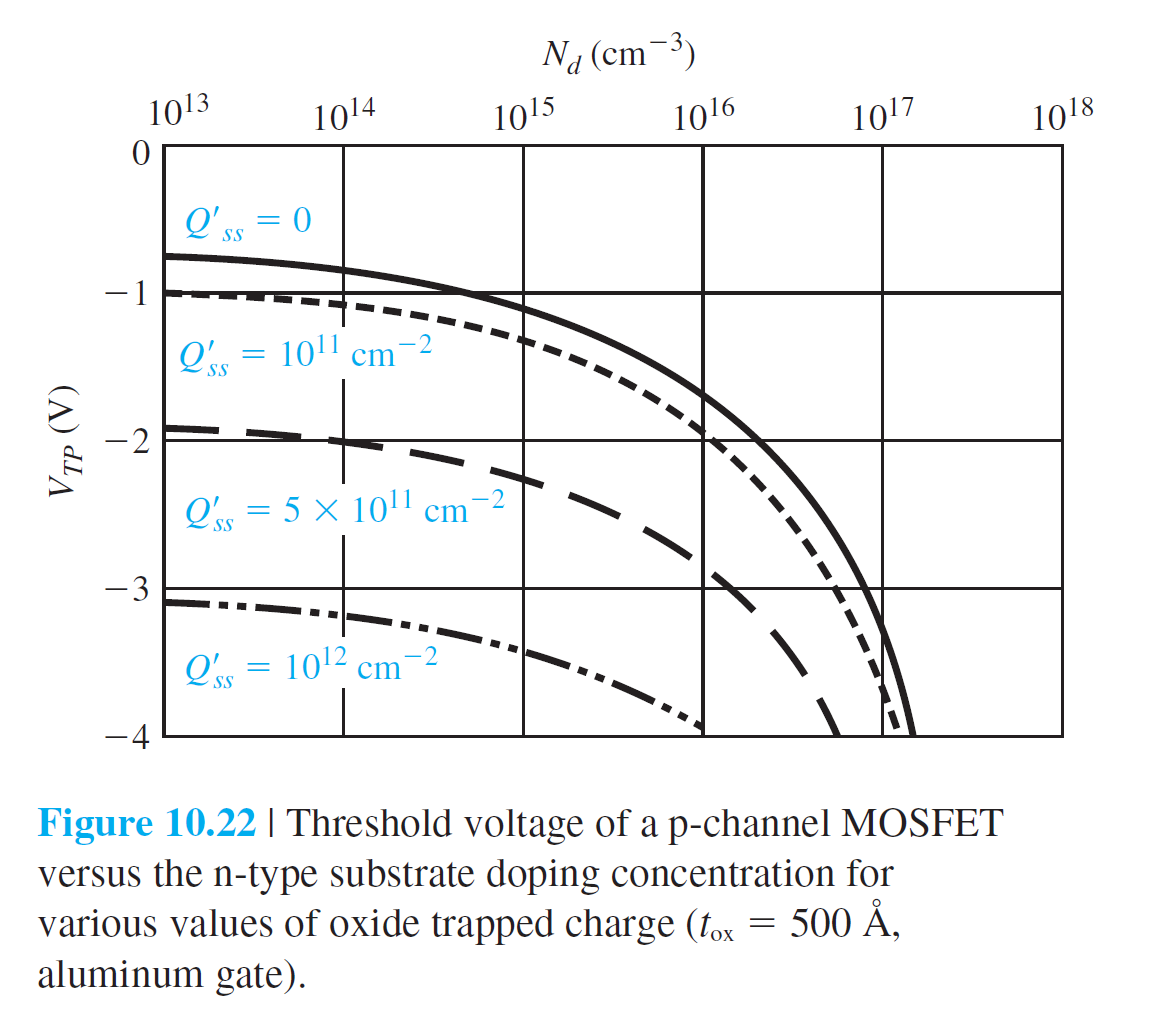


반도체 표면에 inversion 층이 생성되었겠지만, 이를 무시하고, 전하량 보존 법칙을 적용하면, 다음 식을 얻는다. $$ Q_{m T}'+Q_{ss}'=\left|Q_{SD}'(\max )\right| \qquad (10.26) $$ 여기서 $$ \left|Q_{SD}'(\max )\right|=e N_a x_{dT} \qquad (10.27) $$ Gate에 양의 전압을 걸어주면 그림 10.20과 같은 에너지 밴드를 얻는다.

인가된 $V_{GB}$는 $V_{\text {ox }}$와 $\Delta \phi_s$에 변화를 일으킨다. 식 (10.20)과 (10.21)으로부터 다음을 얻는다. $$ V_G=\Delta V_{\text {ox }}+\Delta \phi_s=V_{\text {ox }}+\phi_s+\phi_{ms} $$ Threshold inversion 조건에서 $V_G=V_{TN}$으로 정의하자. $V_{TN}$는 전자 inversion 층을 생기게 하는 threshold 전압이다. 표면 포텐셜 $\phi_s$는 threshold inversion 조건에서 $\phi_s=2 \phi_{Fp}$이므로 다음과 같이 된다. $$ V_{TN}=V_{\text {ox } T}+2 \phi_{Fp}+\phi_{ms} \qquad (10.28) $$ $V_{\mathrm{ox}T}$ threshold inversion 조건에서 $V_{\mathrm{ox}}$이다. $V_{\mathrm{ox}T}$은 전기용량과 관련하여 다음과 같이 주어진다. $$ \begin{aligned} V_{\mathrm{ox}T}&=\frac{Q_{m T}'}{C_{\mathrm{ox}}} \qquad (10.29) \\[10pt] &=\frac{1}{C_{\mathrm{ox}}}\left(\left|Q_{SD}'(\max )\right|-Q_{\mathrm{ss}}'\right) \qquad (10.30) \end{aligned} $$ $C_{\mathrm{ox}}$는 단위 면적당 산화막의 전기용량이다. 결과적으로 threshold 전압은 다음과 같이 주어진다. $$ \begin{aligned} V_{TN}&=\frac{\left|Q_{SD}'(\max )\right|}{C_{\mathrm{ox}}}-\frac{Q_{ss}'}{C_{\mathrm{ox}}}+\phi_{ms}+2 \phi_{Fp} \qquad (10.31a) \\[10pt] &=\left(\left|Q_{SD}'(\max )\right|-Q_{ss}'\right)\left(\frac{t_{\mathrm{ox}}}{\epsilon_{\mathrm{ox}}}\right)+\phi_{ms}+2 \phi_{Fp} \qquad (10.31b) \end{aligned} $$ Flat 밴드 전압에 대한 (10.25)식을 이용하면 다음과 같이 된다. \begin{equation} V_{TN}=\frac{\left|Q_{SD}'(\max )\right|}{C_{\mathrm{ox}}}+V_{FB}+2 \phi_{Fp} \qquad (10.31c) \end{equation} $V_{TN}$는 반도체 도핑, $Q_{ss}'$ 및 산화막 두께 등으로 조절이 가능하다.

만약 $V_{TN} < 0$ V이라면, $V_G = 0$ V일 때도 inversion 층이 존재함을 의미한다. 이러한 소자를 공핍형 소자임을 의미한다. $V_G = 0$ V일 때 inversion 층이 아직 형성되지 않은 소자를 증가형 소자라고 한다. 그림 10.21은 다양한 산화막 전하값들에 대한 $V_{TN}$-$N_a$ 그래프를 보여주고 있다. 증가형 소자를 얻기 위해서는 p형 반도체가 좀더 높은 도핑이 필요함을 알수있다.

N형 반도체 기판에 대해서는 아래 식들이 유도된다. \begin{equation} \begin{aligned} &V_{T P}=\left(-\left|Q_{SD}'(\max )\right|-Q_{ss}'\right)\left(\frac{t_{\mathrm{ox}}}{\epsilon_{\mathrm{ox}}}\right)+\phi_{ms}-2 \phi_{Fn} \qquad (10.32)\\[10pt] &\begin{gathered} \phi_{ms}=\phi_m'-\left(\chi'+\frac{E_g}{2 e}-\phi_{Fn}\right) \qquad (10.33a)\\[10pt] \left|Q_{SD}'(\max )\right|=e N_d x_{dT} \qquad (10.33b)\\[10pt] x_{dT}=\sqrt{\frac{4 \epsilon_s \phi_{Fn}}{e N_d}} \qquad (10.33c) \end{gathered} \end{aligned} \end{equation} \begin{equation} \phi_{Fn}=V_t \ln \left(\frac{N_d}{n_i}\right) \qquad (10.33d) \end{equation}


10.2 전압에 대한 전기용량 특성
MOS 구조에서 전기용량은 다음과 계산될 수 있다.
\begin{equation}
C=\frac{dQ}{dV} \qquad (10.34)
\end{equation}
현재 가해진 전압에 추가적인 전압의 미소 변화 $dV$에 대한 추가적인 전하의 미소 변화 $dQ$를 계산함으로써 전기용량을 계산할 수 있다.
MOS 구조의 전기용량 특성으로부터 많은 정보를 얻을 수 있기 때문에, 전기용량 특성은 매우 중요하다.
10.2.1 이상적인 C-V 특성
산화막내에 포획된 전하가 없는 이상적인 경우에 MOS 구조의 C-V 특성을 알아보자.
MOS 구조의 대표적인 3가지 동작 상태는 축적, 공핍, inversion인데 이 세가지에 대한 전기용량을 구해본다.
그림 10.23(a)는 금속-산화막-반도체(p형)의 MOS구조에서 금속 gate에 음의 전압이 인가된 에너지 다이어그램을 보여준다.
산화막-반도체 계면에 양의 전하가 유도된다.
전하 중성법칙에 의해 도체 표면에서도 음의 전하가 유도된다.
전압의 미소증가에 따른 전하의 미소증가에 대한 표현이 그림 10.23(b)에 잘 나타나있다.
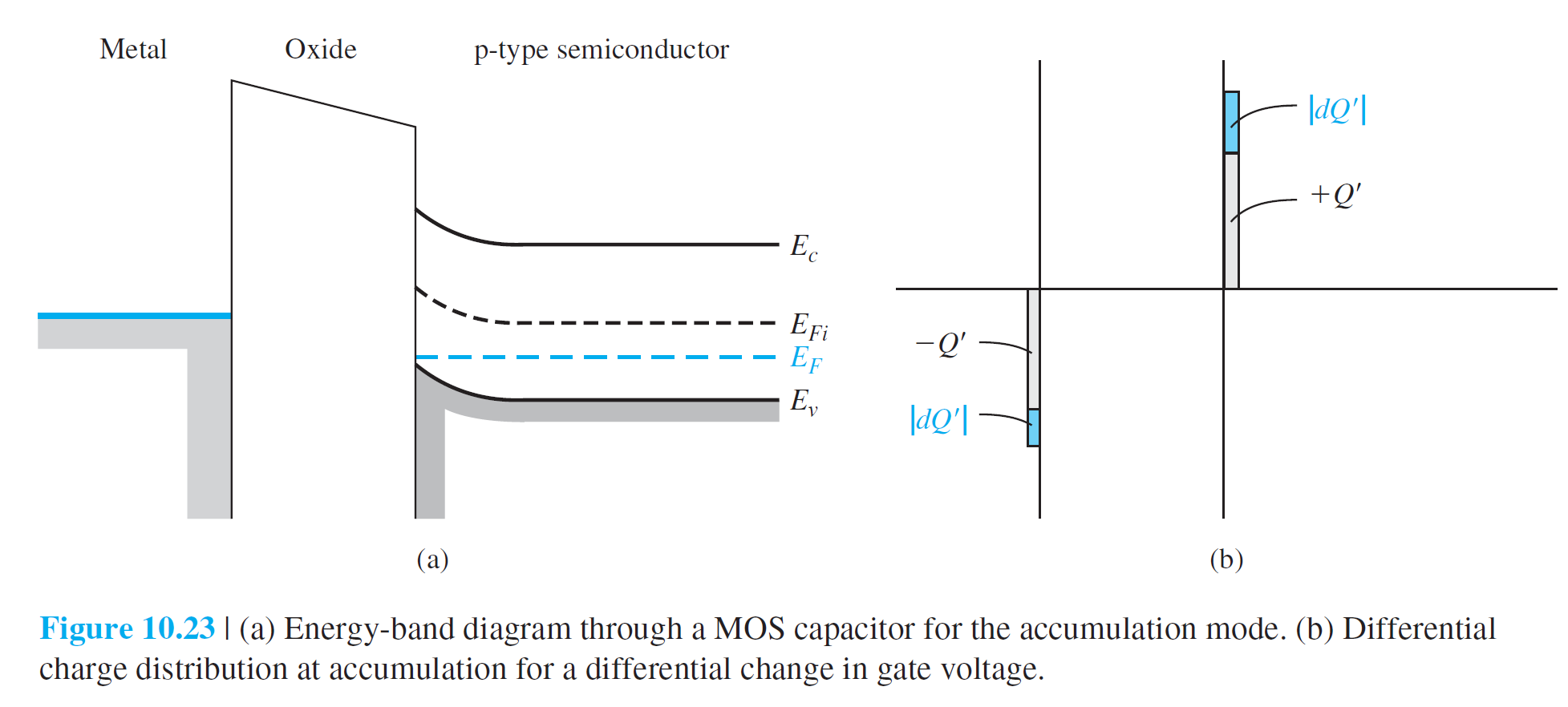
산화막 전기용량 $C'$은 다음과 같이 주어진다. \begin{equation} C'_{축적}=C_{\mathrm{ox}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}} \qquad (10.35) \end{equation} 그림 10.24(a)는 gate에 양의 전압이 인가된 에너지 다이어그램을 보여준다. 아직 inversion 조건에는 도달하지 않아서 반도체에서는 공간전하만이 존재한다. 이에 대응되는 전하분포는 10.24(b)에 잘 나와있다.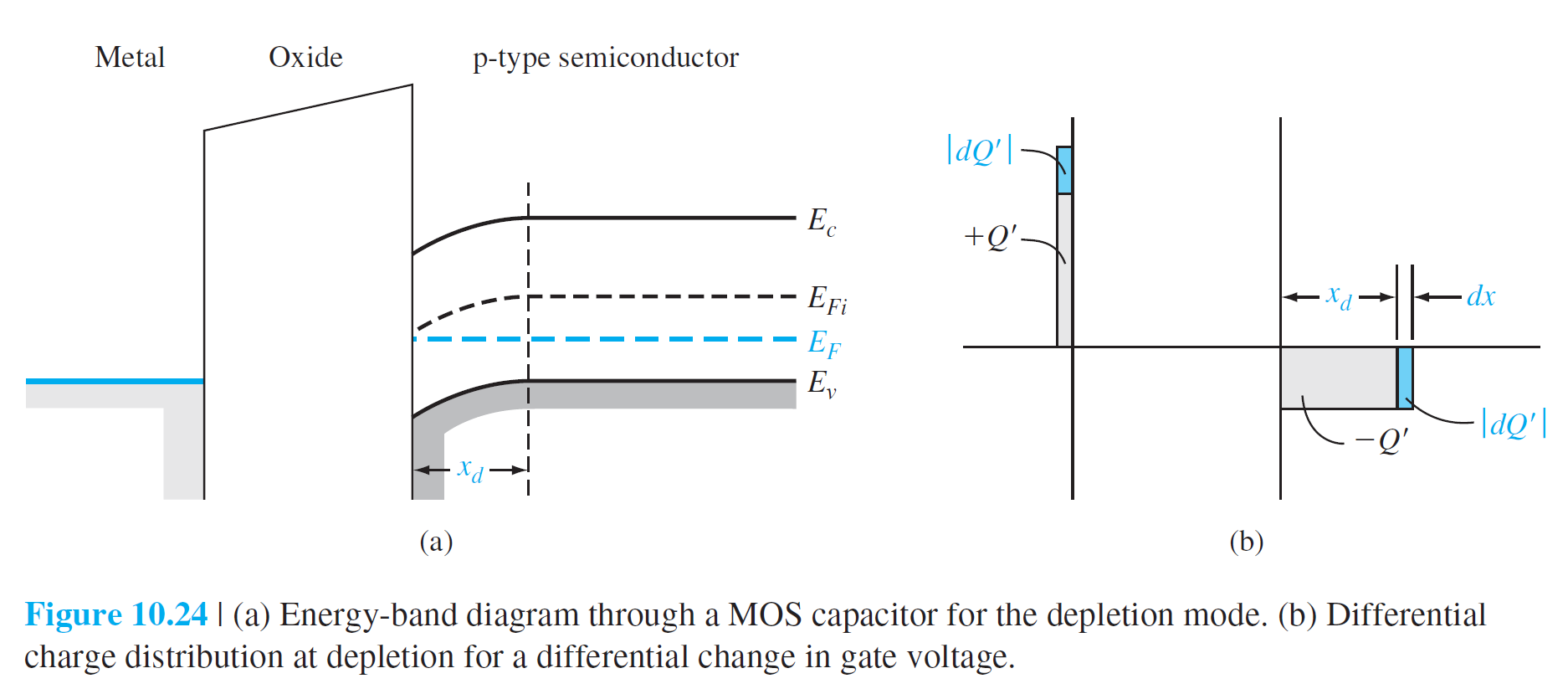
산화막 축전기와 공핍층 축전기는 직렬로 놓여있다고 볼수있다. 공핍 상태의 전기용량은 다음과 같이 주어질 수 있다. $$ \begin{aligned} & \frac{1}{C'_{공핍}}=\frac{1}{C_{\mathrm{ox}}}+\frac{1}{C_{SD}'} \qquad (10.36a)\\[10pt] & C'_{공핍}=\frac{C_{\mathrm{ox}} C_{SD}'}{C_{\mathrm{ox}}+C_{SD}'} \qquad (10.36b) \end{aligned} $$ $C_{\mathrm{ox}} = \epsilon_{\mathrm{ox}}/t_{\mathrm{ox}}$이고 $C_{SD}'=\epsilon_s/x_d$이므로 $$ C'_{공핍}=\frac{C_{\mathrm{ox}}}{1+\frac{C_{\mathrm{ox}}}{C_{SD}'}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) x_d} \qquad (10.37) $$ Threshold inversion 조건에서 전기용량은 다음과 같다. $$ C_{\min }'=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) x_{dT}} \qquad (10.38) $$
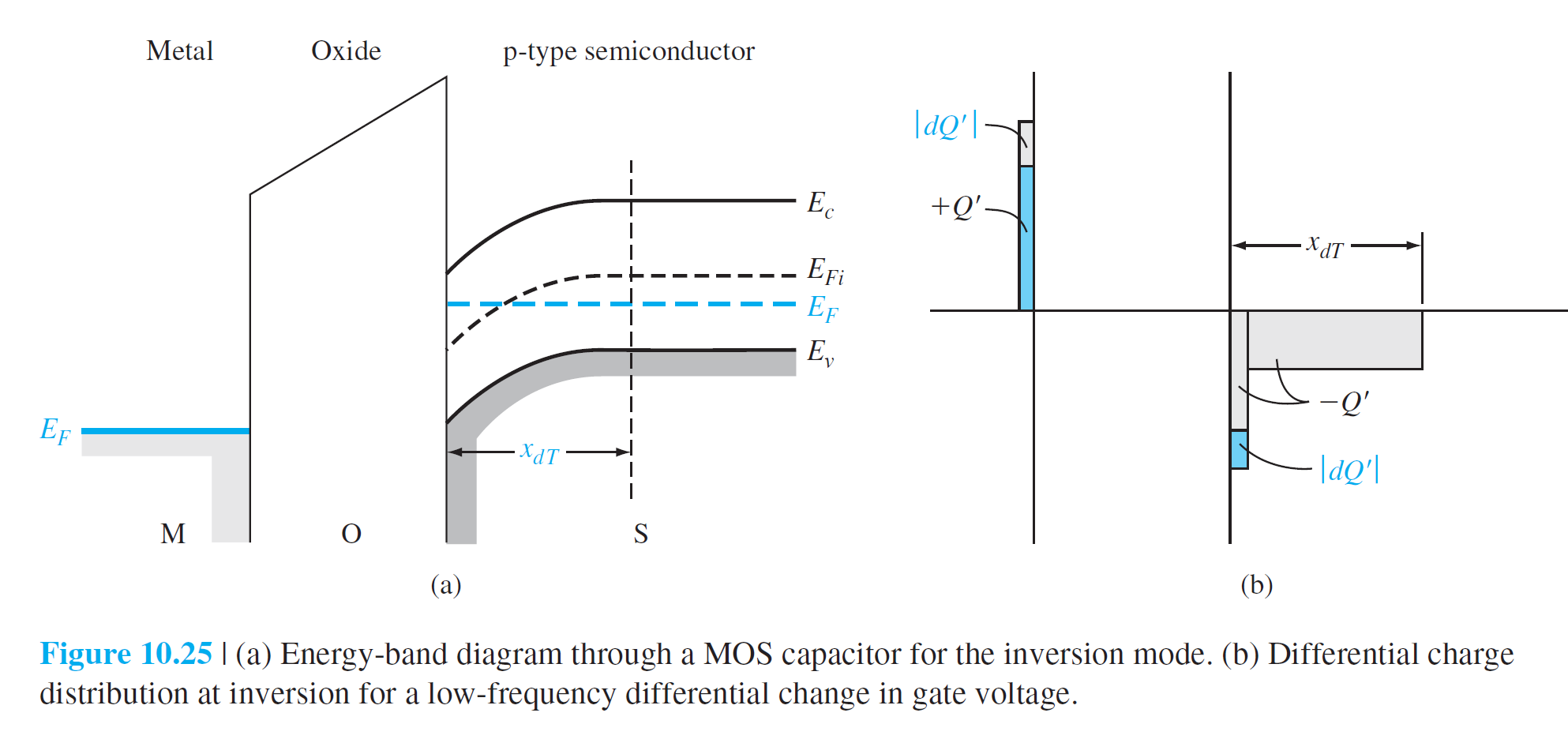
그림 10.25는 inversion 층이 존재하는 경우의 에너지 밴드와 전하분포를 보여준다. 전압의 미소증가가 있을 경우 공핍층의 폭은 이미 최대치에 도달했기 때문에 공간전하의 변화는 더 이상 없고, 표면전하의 변화만 있다. 이 경우 전기용량은 다음과 같이 (10.35)와 동일하게 주어진다. $$ C'(\text { inv })=C_{\mathrm{ox}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}} \qquad (10.39) $$
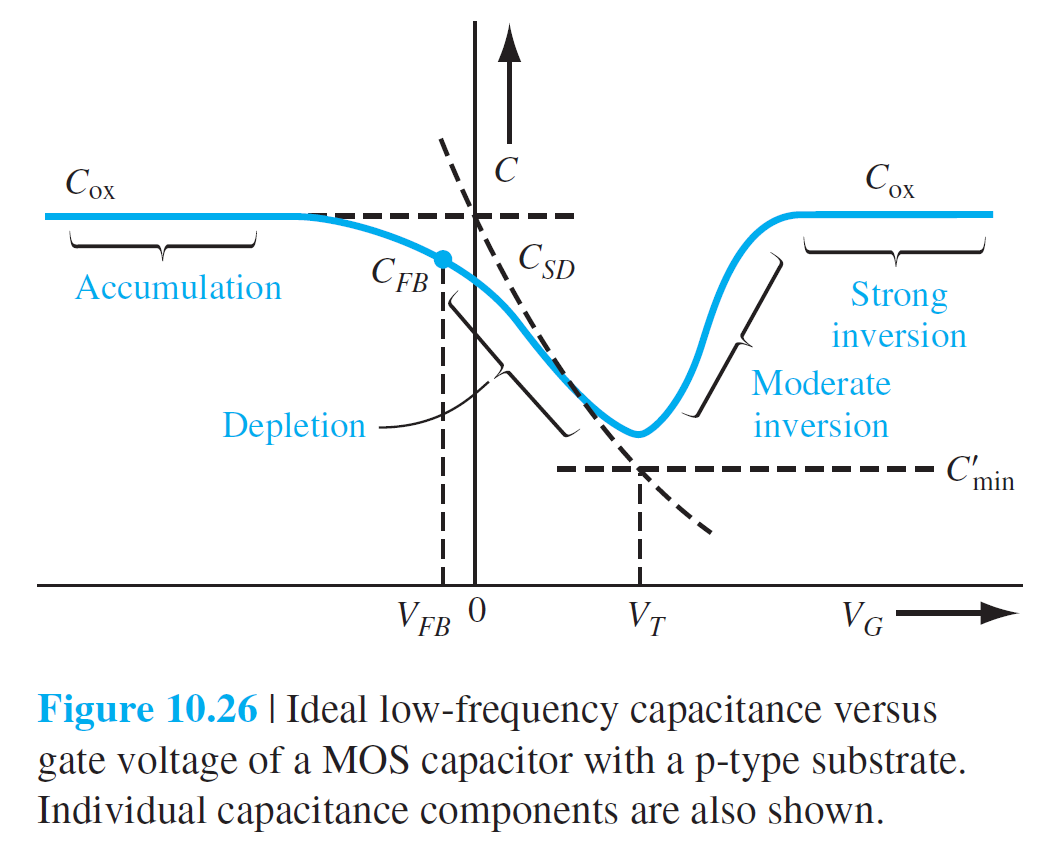
Flat 밴드 조건에서 전기용량은 다음과 같이 주어진다. \begin{equation} C_{FB}'=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) \sqrt{\frac{kT}{e}\left(\frac{\epsilon_s}{e N_a}\right)}} \qquad (10.40) \end{equation}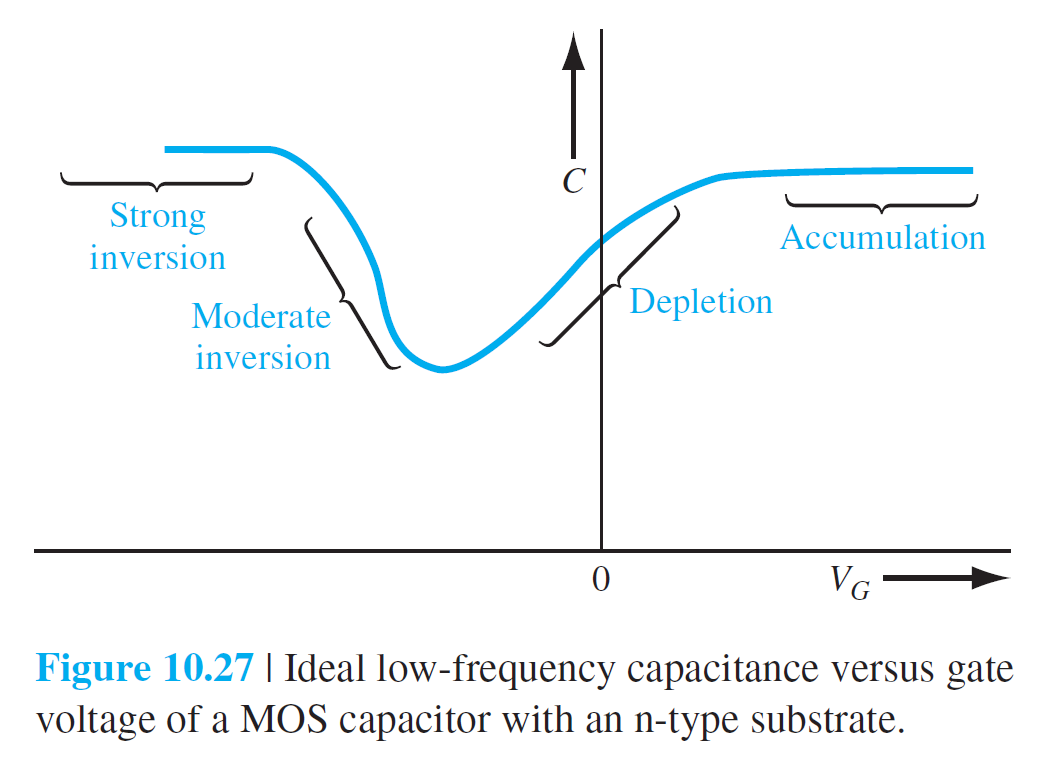


산화막 전기용량 $C'$은 다음과 같이 주어진다. \begin{equation} C'_{축적}=C_{\mathrm{ox}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}} \qquad (10.35) \end{equation} 그림 10.24(a)는 gate에 양의 전압이 인가된 에너지 다이어그램을 보여준다. 아직 inversion 조건에는 도달하지 않아서 반도체에서는 공간전하만이 존재한다. 이에 대응되는 전하분포는 10.24(b)에 잘 나와있다.

산화막 축전기와 공핍층 축전기는 직렬로 놓여있다고 볼수있다. 공핍 상태의 전기용량은 다음과 같이 주어질 수 있다. $$ \begin{aligned} & \frac{1}{C'_{공핍}}=\frac{1}{C_{\mathrm{ox}}}+\frac{1}{C_{SD}'} \qquad (10.36a)\\[10pt] & C'_{공핍}=\frac{C_{\mathrm{ox}} C_{SD}'}{C_{\mathrm{ox}}+C_{SD}'} \qquad (10.36b) \end{aligned} $$ $C_{\mathrm{ox}} = \epsilon_{\mathrm{ox}}/t_{\mathrm{ox}}$이고 $C_{SD}'=\epsilon_s/x_d$이므로 $$ C'_{공핍}=\frac{C_{\mathrm{ox}}}{1+\frac{C_{\mathrm{ox}}}{C_{SD}'}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) x_d} \qquad (10.37) $$ Threshold inversion 조건에서 전기용량은 다음과 같다. $$ C_{\min }'=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) x_{dT}} \qquad (10.38) $$

그림 10.25는 inversion 층이 존재하는 경우의 에너지 밴드와 전하분포를 보여준다. 전압의 미소증가가 있을 경우 공핍층의 폭은 이미 최대치에 도달했기 때문에 공간전하의 변화는 더 이상 없고, 표면전하의 변화만 있다. 이 경우 전기용량은 다음과 같이 (10.35)와 동일하게 주어진다. $$ C'(\text { inv })=C_{\mathrm{ox}}=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}} \qquad (10.39) $$

Flat 밴드 조건에서 전기용량은 다음과 같이 주어진다. \begin{equation} C_{FB}'=\frac{\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}+\left(\frac{\epsilon_{\mathrm{ox}}}{\epsilon_s}\right) \sqrt{\frac{kT}{e}\left(\frac{\epsilon_s}{e N_a}\right)}} \qquad (10.40) \end{equation}


10.2.2 주파수 효과
그림 10.25는 p형 반도체 기판을 가진 inversion 상태를 기술하고 있다.
이 inversion 층의 전자의 농도에 영향을 주는 전자공급원은 다음 두 가지가 있다.
• p형 반도체 내의 소수 운반자인 전자
• 공핍층에서 쌍 생성된 전자-홀
위 두 과정은 PN 접합 다이오드에서 역전압이 가해질 때의 과정과 동일하다. 가해지는 교류전압에 대해 위 두 과정은 둔감하게 반응하여, C-V 특성은 교류전압 주파수의 함수가 된다.
그림 10.28은 p형 반도체기판을 가진 MOS 축전기에서 threshold 조건일 때의 전하분포를 보여준다. 고주파수에서는 inversion 층의 전하는 반응하지 않고, 공핍층 전하량만 반응한다. 그림 10.28에 해당하는 전기용량은 $C_{\min}'$이 된다.
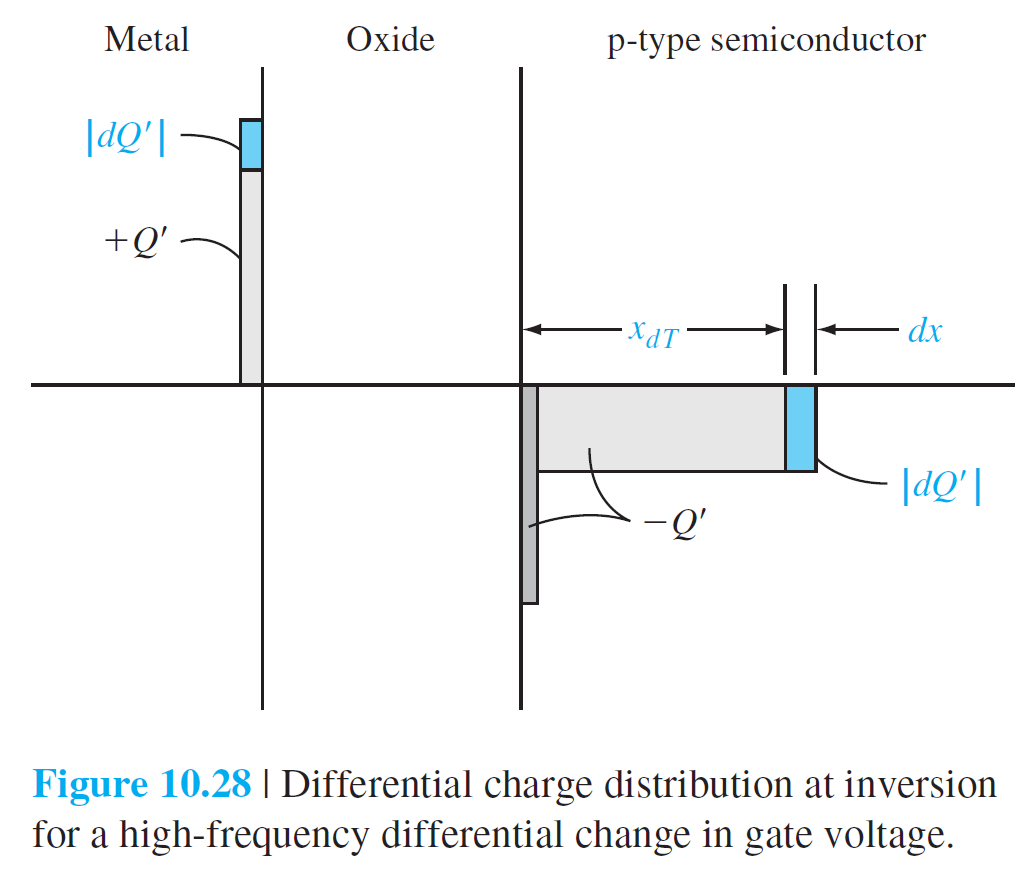
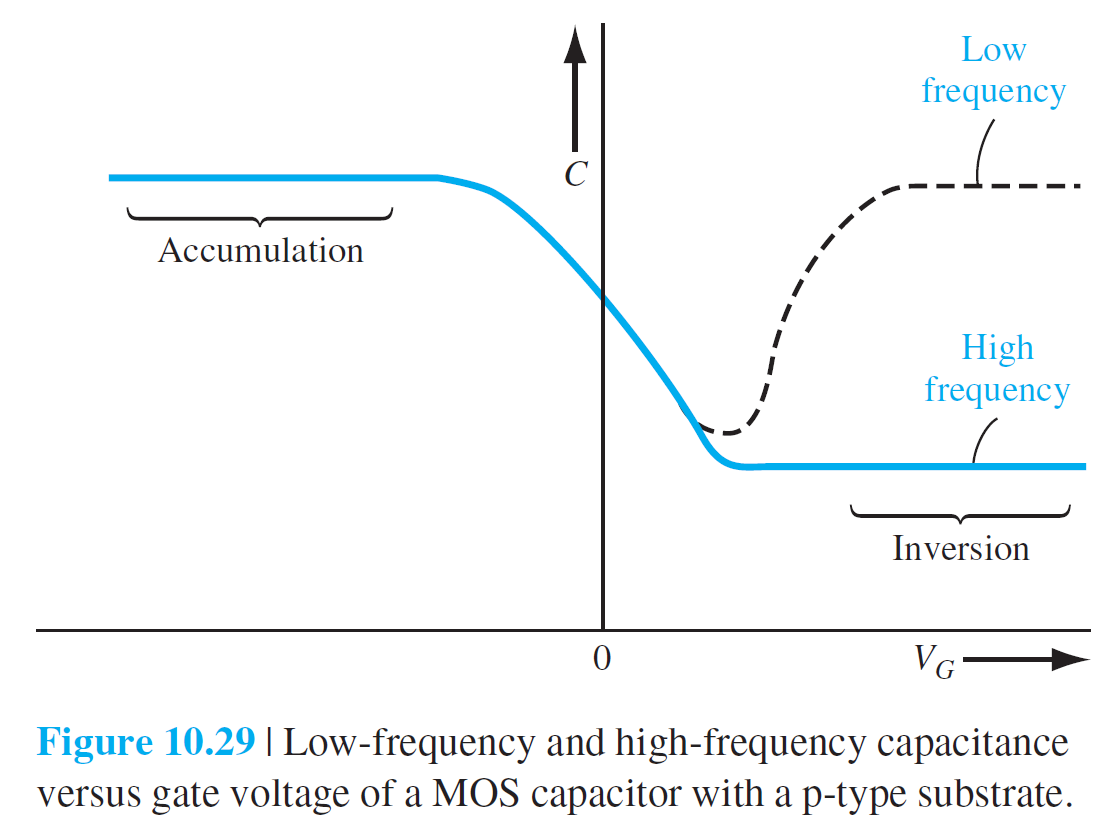
그림 10.29에는 고주파와 저주파에서의 C-V 특성이 보여진다. 고주파는 1 MHz 정도이고, 저주파는 5~100 Hz 정도이다.
• p형 반도체 내의 소수 운반자인 전자
• 공핍층에서 쌍 생성된 전자-홀
위 두 과정은 PN 접합 다이오드에서 역전압이 가해질 때의 과정과 동일하다. 가해지는 교류전압에 대해 위 두 과정은 둔감하게 반응하여, C-V 특성은 교류전압 주파수의 함수가 된다.
그림 10.28은 p형 반도체기판을 가진 MOS 축전기에서 threshold 조건일 때의 전하분포를 보여준다. 고주파수에서는 inversion 층의 전하는 반응하지 않고, 공핍층 전하량만 반응한다. 그림 10.28에 해당하는 전기용량은 $C_{\min}'$이 된다.

그림 10.29에는 고주파와 저주파에서의 C-V 특성이 보여진다. 고주파는 1 MHz 정도이고, 저주파는 5~100 Hz 정도이다.

10.2.3 고정 산화막과 경계면 전하 효과
지금까지의 C-V 특성의 논의에서는 산화막 경계에 고정된 전하가 없는 이상적인 경우로 한정되었다.
이 산화막 경계의 고정전하를 고려한다면 C-V 특성 또한 변화가 생길것이다.
Flat 밴드 전압은 다음과 같이 주어진다.
\begin{equation}
V_{FB}=\phi_{ms}-\frac{Q_{ss}'}{C_{\mathrm{ox}}}
\end{equation}
이 식이 의미하는 것은 고정 산화막 전하 $Q_{ss}'$가 증가할수록 $V_{FB}$가 음의 전압으로 감소하는 것을 의미한다.
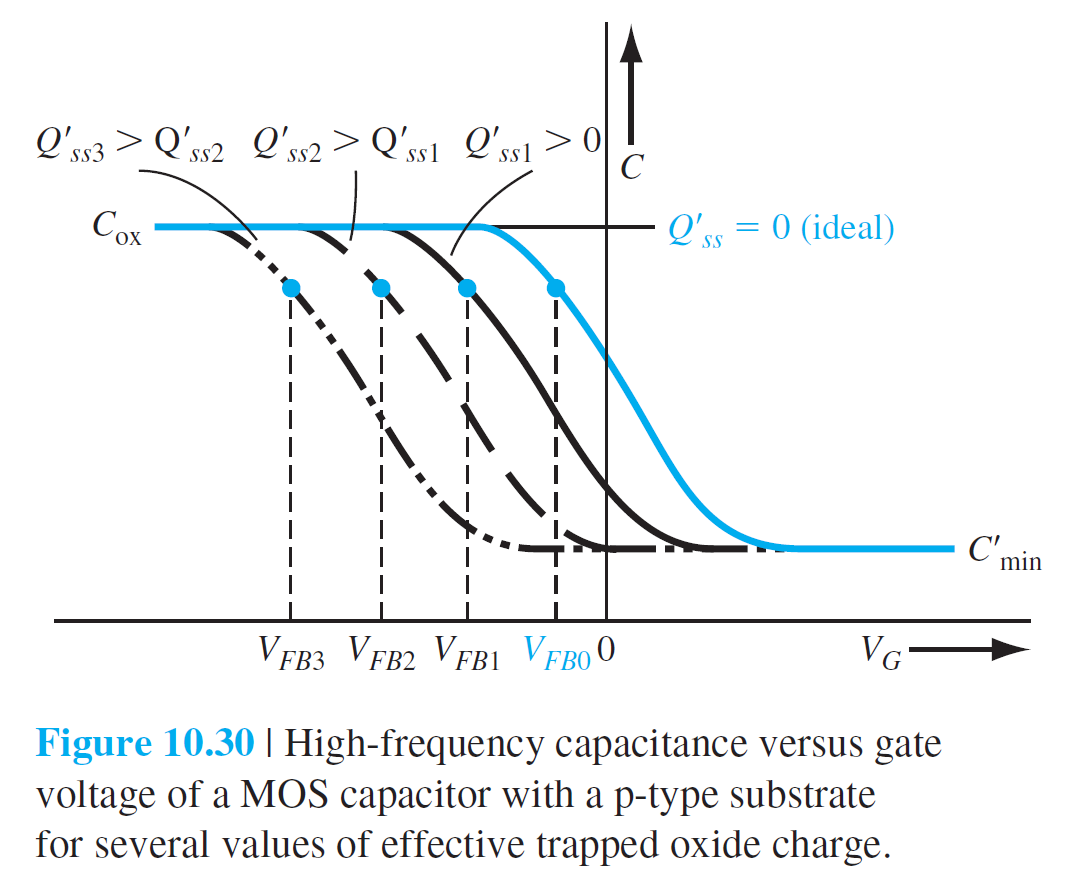
이러한 효과는 그림 10.30에 보여진다.
MOS구조에 대해서 $\phi_{ms}$와 $C_{\mathrm{ox}}$가 알려지면, 이상적인 $V_{FB}$가 결정될수있다.
그림 10.30이 말해주는 것은 실험적인 C-V 특성으로부터 $Q_{ss}'$를 예측할 수 있다는 것이다.
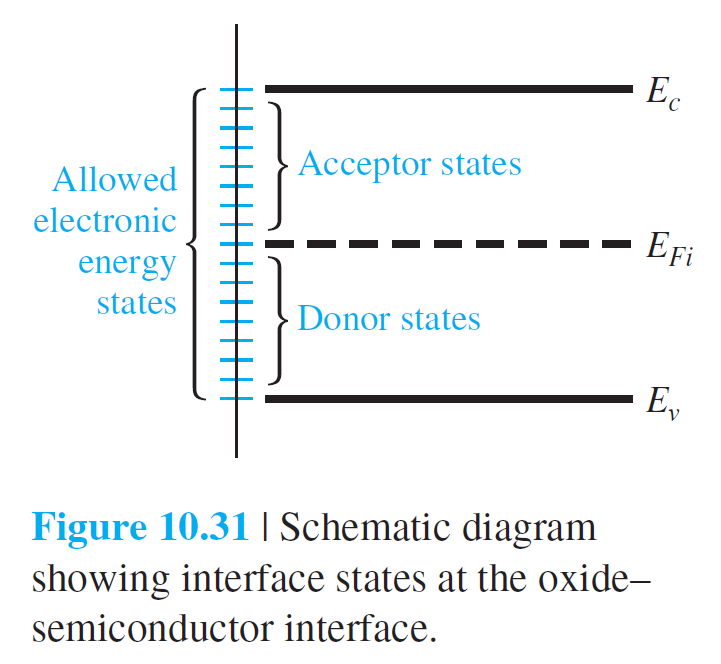
반도체의 경계에서도 금지대 내에 전자들이 존재할 수 있는 상태들이 있을 수 있다. 이 상태들은 그림 10.31에 잘 나타나 있다. 일반적으로 금지대 중간 위부분은 acceptor 상태들, 중간 아래는 donor 상태들이 존재한다.
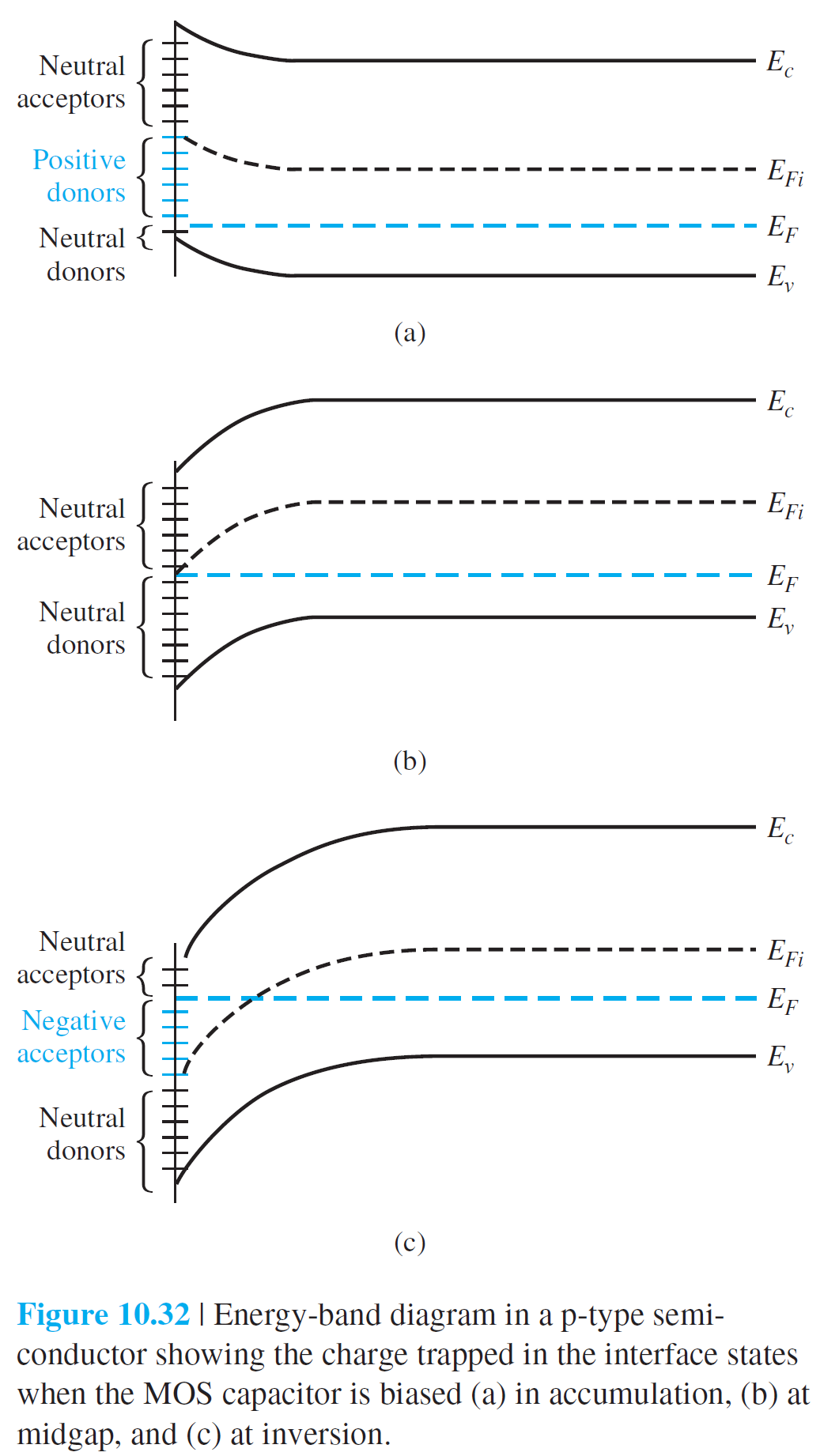
몇몇 $V_G$에 대해서 축적 상태, 중간갭 상태, inversion 상태가 형성될 수 있고, 이 상태들에서의 에너지 밴드가 그림 10.32에 보여지고 있다.
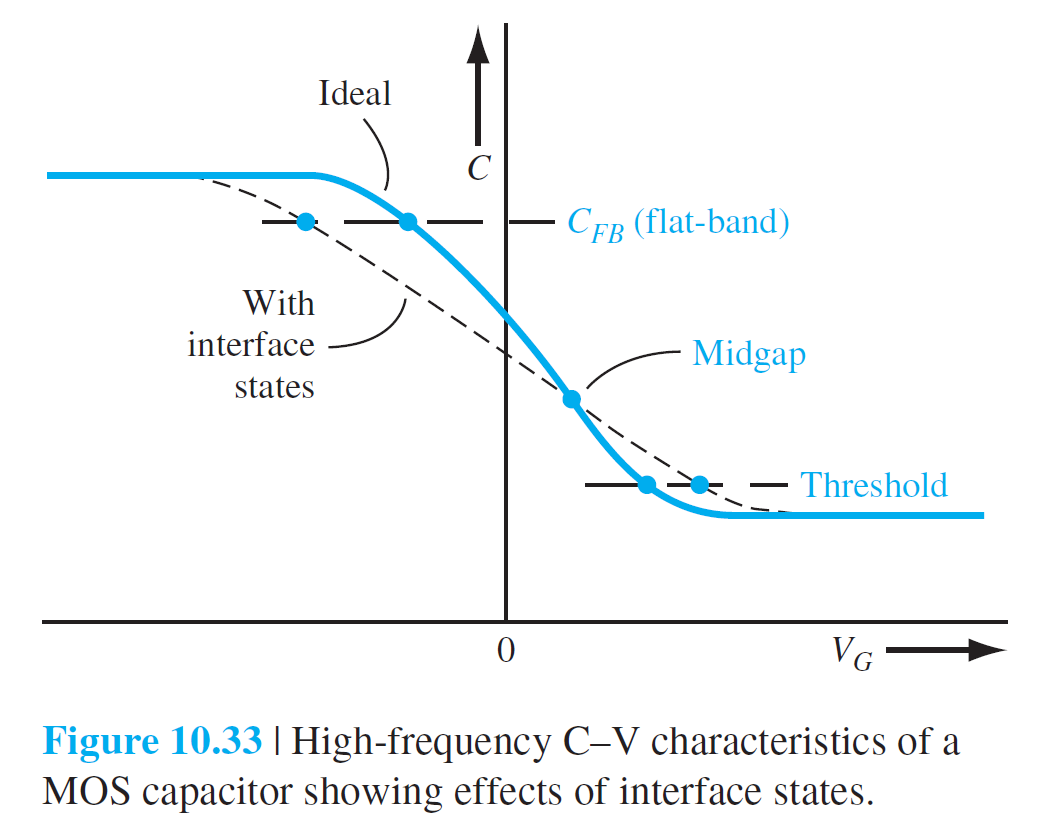
반도체의 경계에 존재하는 전하에 의한 C-V 특성은 그림 10.33에 보여지고 있다.

반도체의 경계에서도 금지대 내에 전자들이 존재할 수 있는 상태들이 있을 수 있다. 이 상태들은 그림 10.31에 잘 나타나 있다. 일반적으로 금지대 중간 위부분은 acceptor 상태들, 중간 아래는 donor 상태들이 존재한다.

몇몇 $V_G$에 대해서 축적 상태, 중간갭 상태, inversion 상태가 형성될 수 있고, 이 상태들에서의 에너지 밴드가 그림 10.32에 보여지고 있다.

반도체의 경계에 존재하는 전하에 의한 C-V 특성은 그림 10.33에 보여지고 있다.

10.3 기본적인 MOSFET 동작
10.3.1 MOSFET 구조
4가지 기본적인 MOSFET이 있다.
• n채널 증가형 MOSFET
• n채널 공핍형 MOSFET
• p채널 증가형 MOSFET
• p채널 공핍형 MOSFET
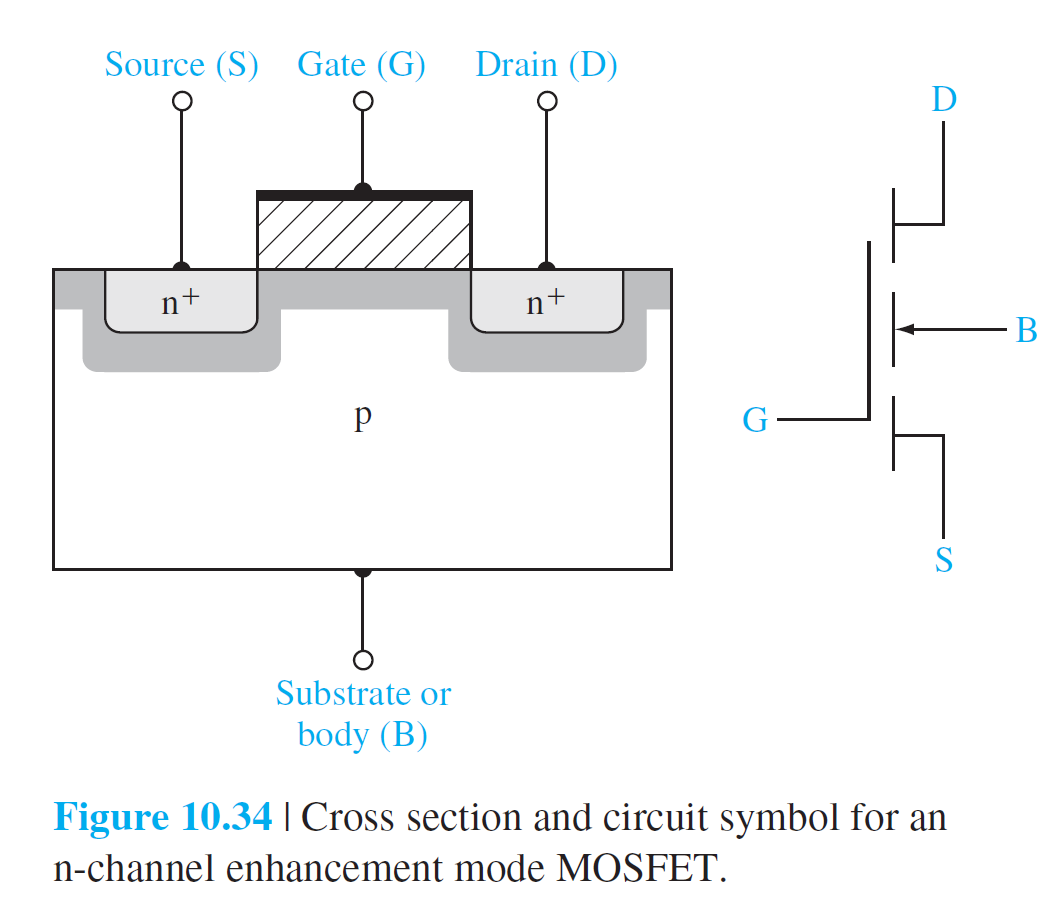
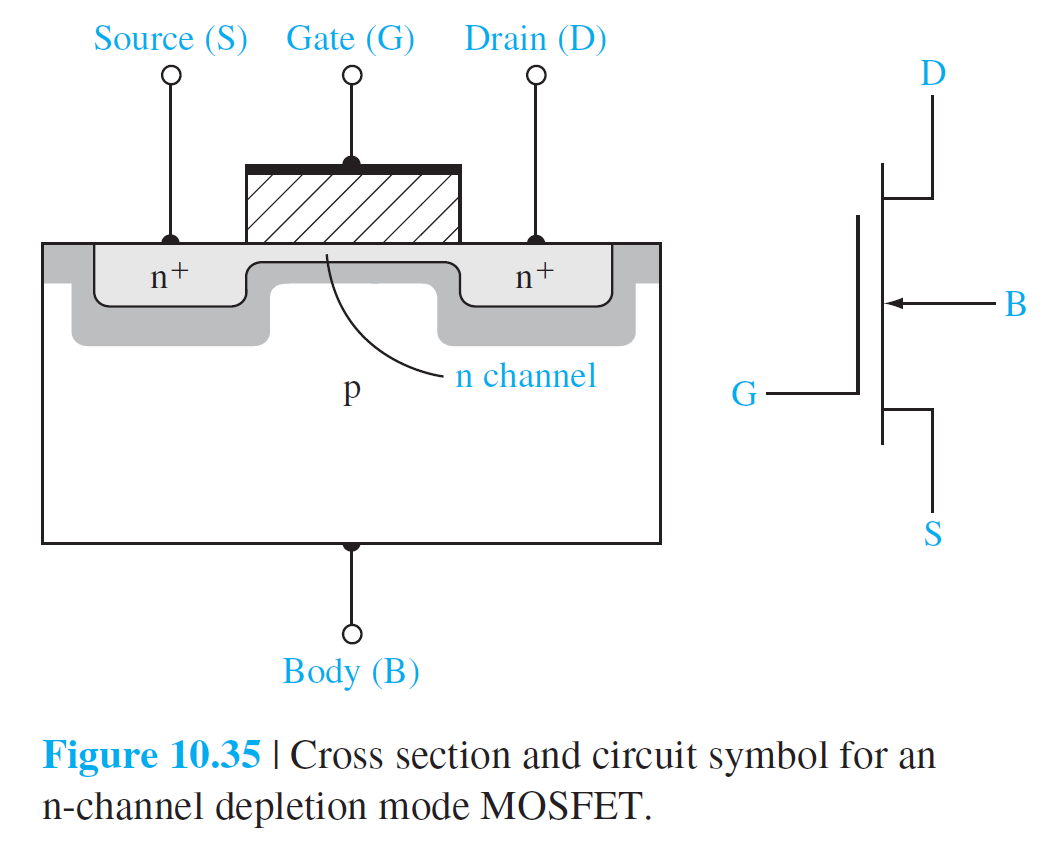
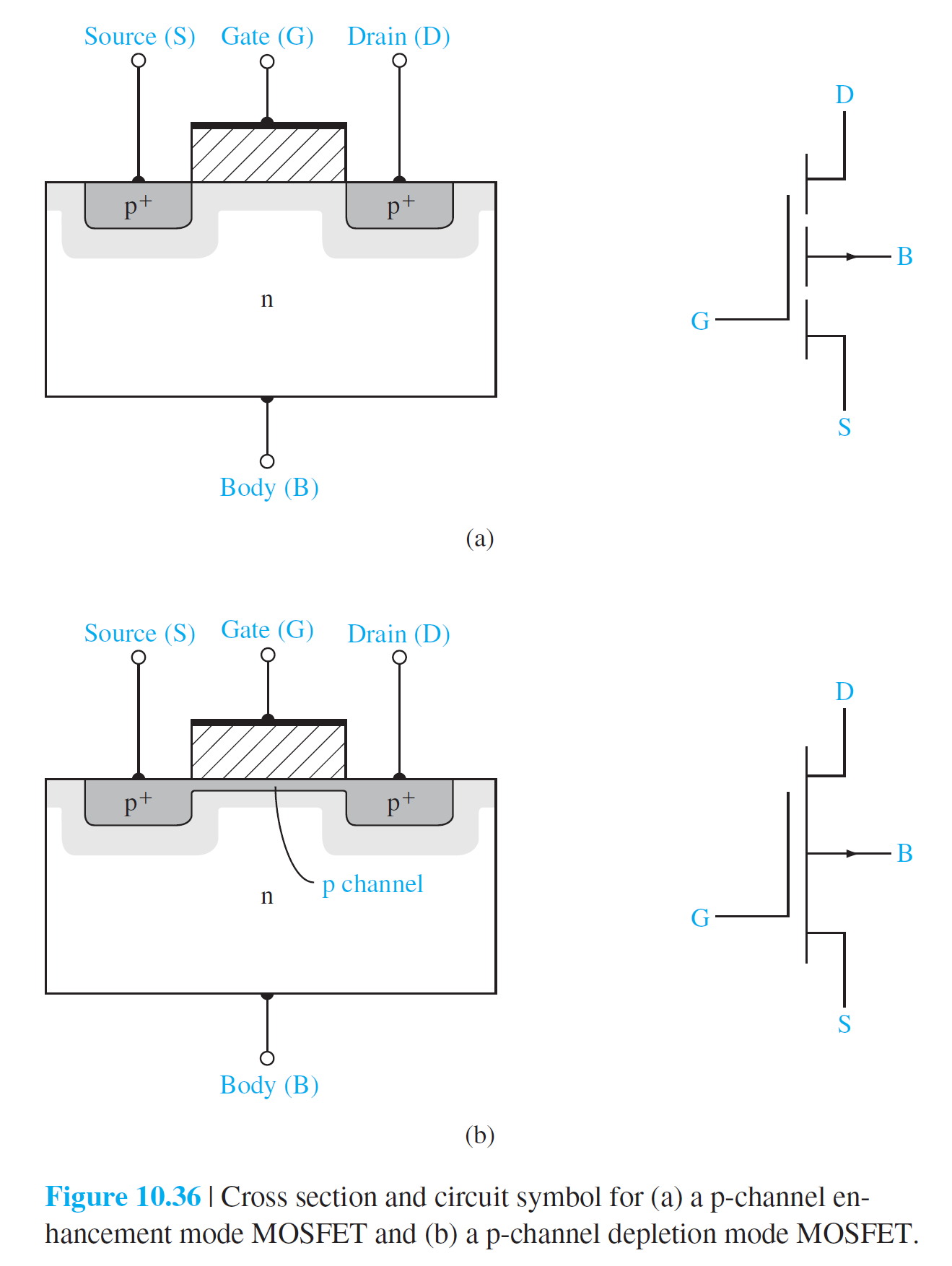
• n채널 증가형 MOSFET
• n채널 공핍형 MOSFET
• p채널 증가형 MOSFET
• p채널 공핍형 MOSFET



10.3.2 I-V 곡선
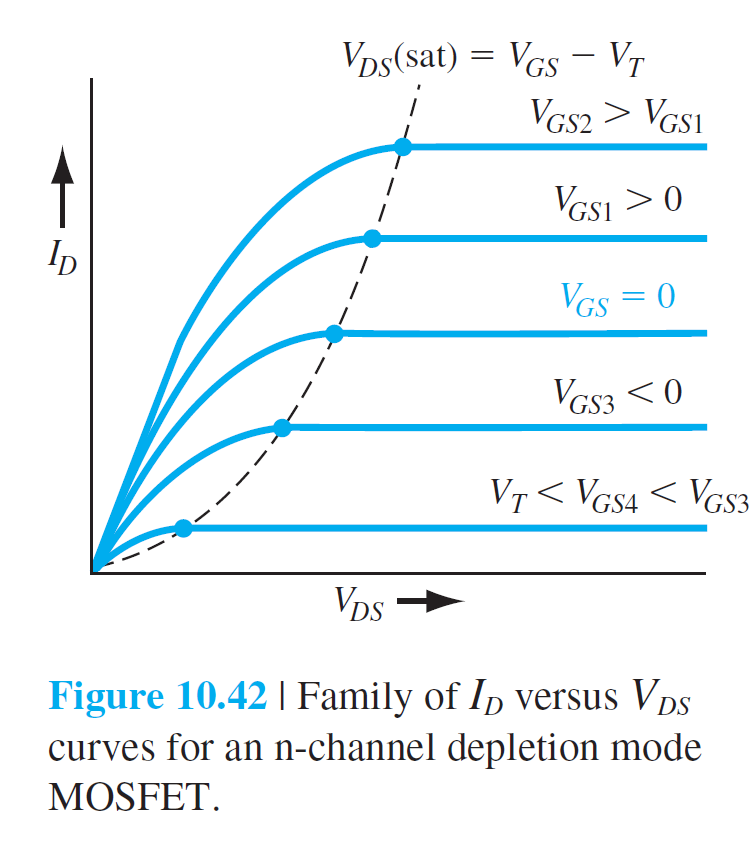
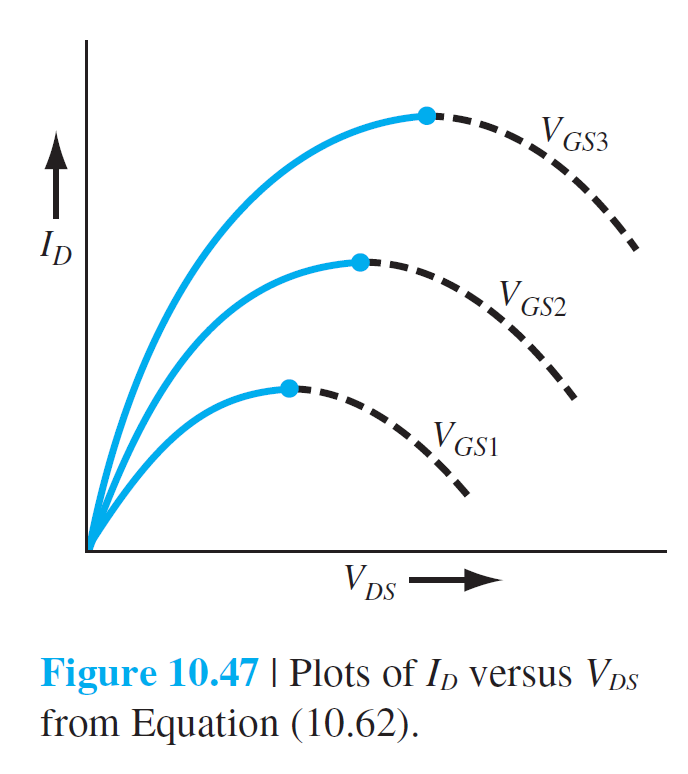
그림 37은 n채널 증가형 MOSFET을 보여주는데,
$V_D$가 가해진 상태에서 $V_G < V_T$일 때(a)와 $V_G > V_T$일 때의 전하 분포를 보여준다.
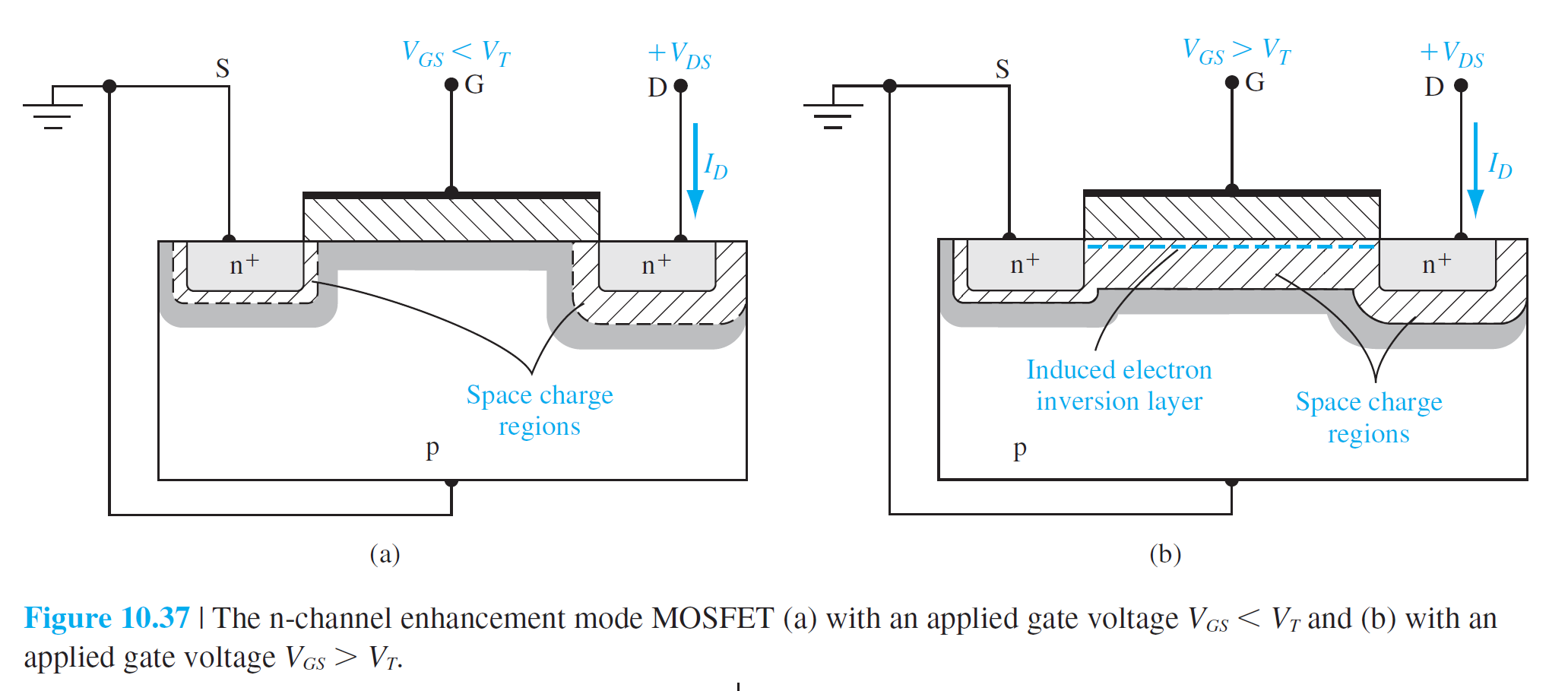
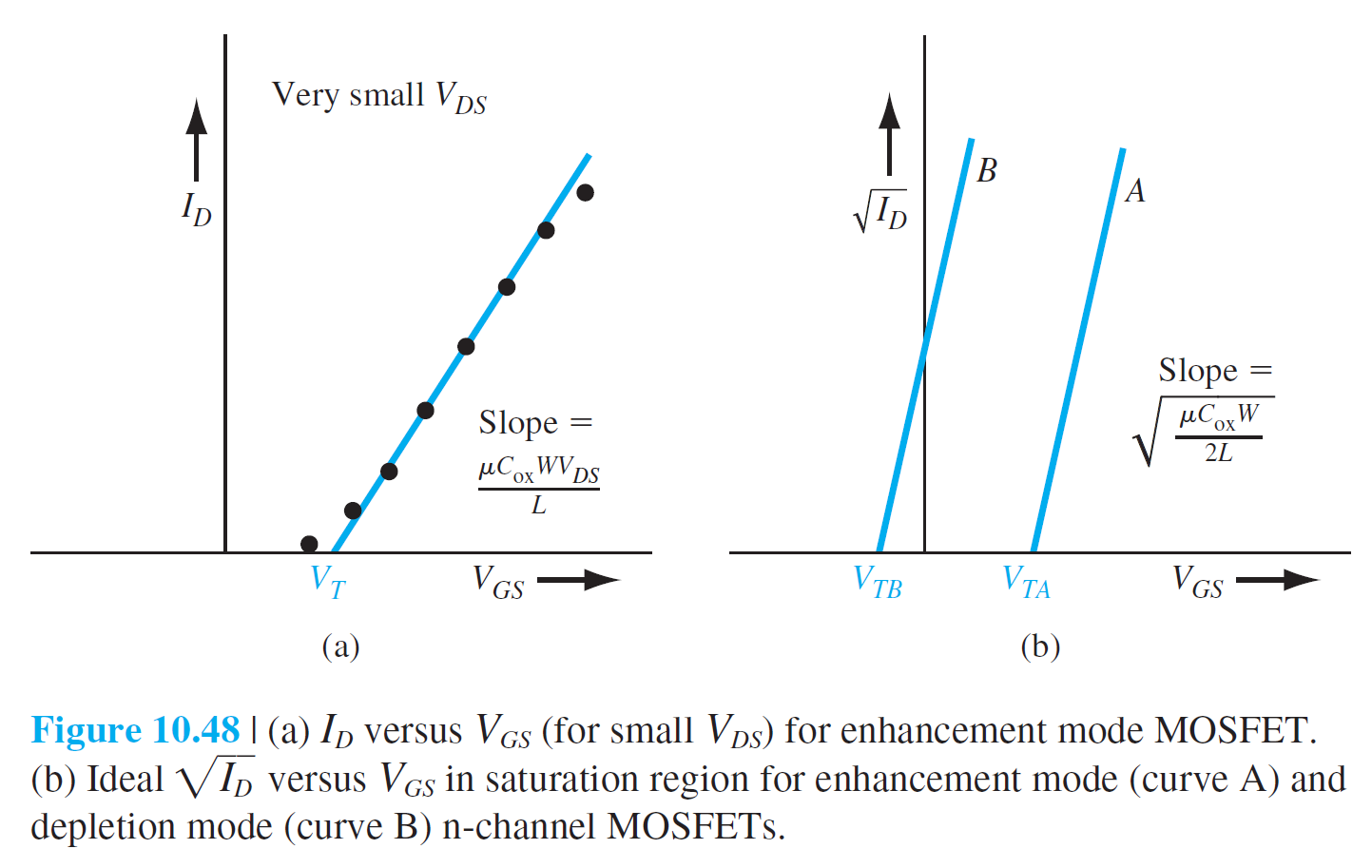
$V_{DS}$는 source와 drain사이에 걸린 전압을 의미하며, 이것이 매우 작을때는 아래와 같은 $I_D$와 다음과 같은 선형 관계를 가진다고 할수있다. $$ I_D=g_d V_{DS} \qquad (10.41) $$ 여기서 $I_D$는 drain으로 흐르는 전류를 의미하고, $g_d$는 다음과 같이 주어지는데 $V_{DS}$가 거의 0일때의 채널 전도도를 의미한다. $$ g_d=\frac{W}{L} \cdot \mu_n\left|Q_n'\right| \qquad (10.42) $$ 여기서 각 기호들의 정의는 다음과 같다.
그림 10.38은 $V_{DS}$가 작을때 $I_D-V_{DS}$ 특성을 보여준다.
$V_{GS} < V_T$에서는 $I_D = 0$이고, $V_{GS} > V_T$에서는 $V_{DS}$가 증가함에 따라 $I_D$가 선형적으로 증가하는 것을 보여준다.
더 큰 $V_{GS}$에서 $I_D-V_{DS}$가 더 큰 기울기를 보여주는 것은 inversion 층의 전자농도가 증가했음을 의미한다.
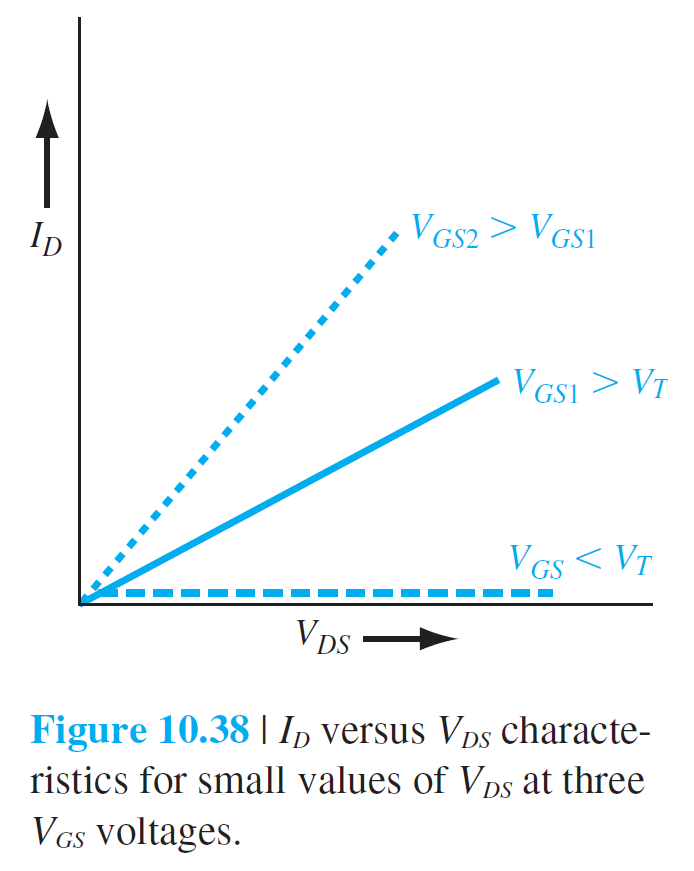
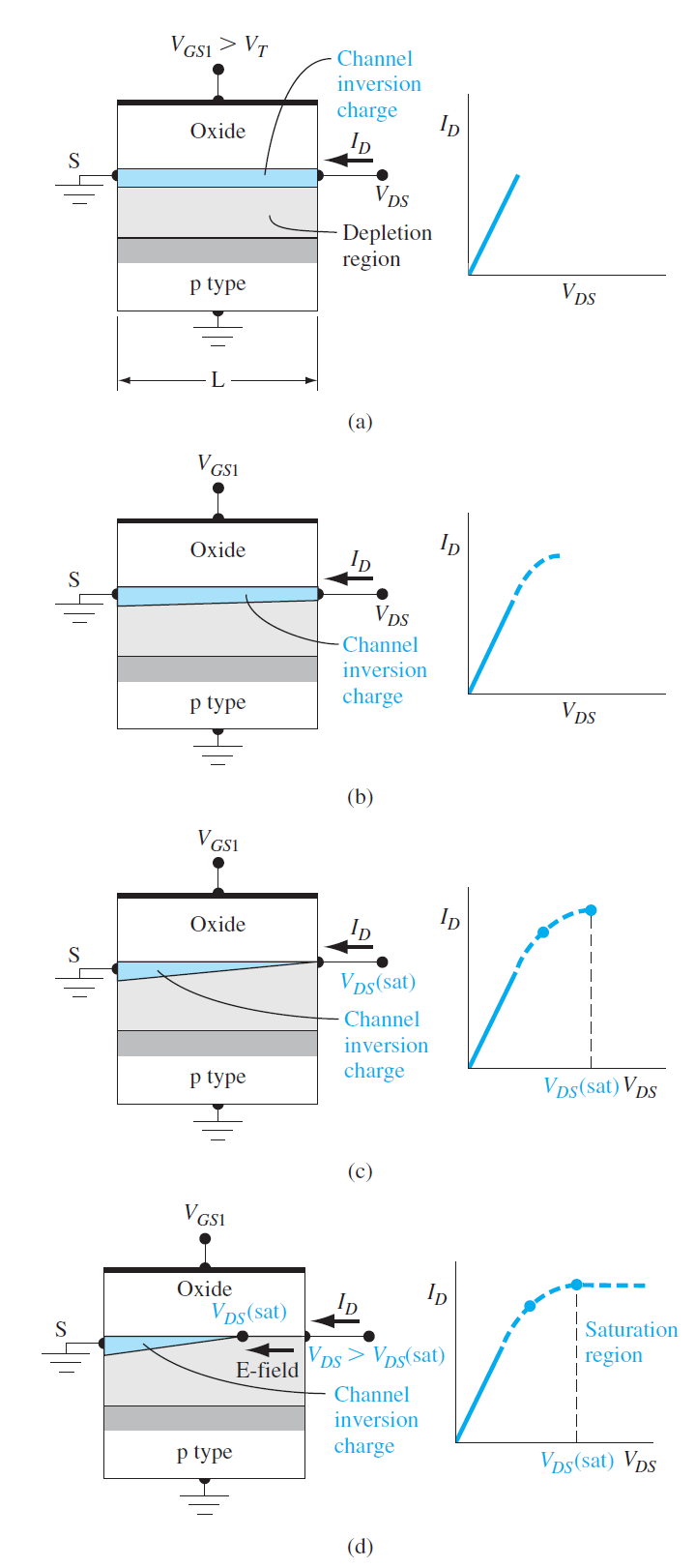
그림 10.39는 $V_{GS} > V_T$에서 전하분포와 $I_D-V_{DS}$의 전체적인 경향을 보여주고 있다. 각 그림에 대한 상세 설명은 다음과 같다.
• 그림 10.39(a)
$V_{DS}$가 매우 작을 경우에는 $I_D$가 $V_{DS}$에 선형적으로 증가한다. inversion 층의 두께는 전체 채널에 대해서 거의 일정하다.
• 그림 10.39(b)
$V_{DS}$가 좀더 증가하게 되면, source에서 drain 쪽으로 갈수록 채널 영역의 inversion 층의 두께가 감소한다. 이것은 $V_{DS}$로 인하여 채널 영역의 모든 영역에서 포텐셜이 같지 않게 되었기 때문이다. Gate, source, drain이 각각 $V_{G}$, $V_{S}$, $V_{D}$의 포텐셜에 있다면, source 측에서 gate로 부터 느끼는 전압 $V_{SG}$과 drain 측에서 gate로 부터 느끼는 전압 $V_{DG}$는 다른 값을 가지게 된다. 그래서 $V_{DG}$는 $V_{SG}$보다 작은 값을 가질 수 있다. 이러한 방식으로 source에서 drain으로 갈수록 inversion 전자농도가 감소하게 된다. 이 inversion 층 두께의 감소로 인하여 전도도가 감소하는데 이것은 $I_D-V_{DS}$곡선에서 기울기의 감소로 나타난다.
• 그림 10.39(c)
$V_{DS}$가 좀더 증가하게 되어, $V_{DG}$가 $V_T$와 같아지게 되는 조건이 될수있다. 이 경우 drain쪽 채널에 형성된 inversion 전자농도는 0이 된다. 그러면 전도도는 0이 되고, $I_D-V_{DS}$이 기울기는 0이된다. 이러한 상태를 다음 식으로 표현할 수 있다.
\begin{aligned} &V_{G} -V_{D} = V_T \\[10pt] &V_{GS}-V_{DS}(\mathrm{sat})=V_T \qquad (10.43a)\\[10pt] &V_{DS}(\mathrm{sat})=V_{GS}-V_T \qquad (10.43b) \end{aligned} 여기서 $V_{DS}(\mathrm{sat})$는 drain 단자에서 inversion 전자농도가 0이 되는 전압을 의미한다.
• 그림 10.39(d)
$V_{DS} > V_{DS}(\mathrm{sat})$인 상태에서 $V_{DS}$가 계속 증가하면, inversion 전자농도가 0이되는 지점은 source 쪽으로 이동한다. 전자들은 inversion 층에서 전기장에 의해 공핍층을 가로질러 drain 쪽으로 이동을 하게 된다. 이 경우 $I_D$는 $V_{DS}$에 무관하게 일정한 값을 가지게 되는데, 이 영역을 포화영역(saturation region)이라고 한다.
기타자료
비포화영역에서 $I_D-V_{DS}$ 그래프는 다음과 같이 주어진다. $$ I_D=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44a) $$ 위 식은 다음과 같이 쓸수있다. $$ \begin{aligned} I_D&=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44b)\\[10pt] I_D&=K_n\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44c) \end{aligned} $$ $k_n'=\mu_n C_{\mathrm{ox}}$는 n 채널 MOSFET에서 공정 전도 파라미터(process conduction parameter)라고 하며, A/V$^2$의 단위를 사용한다.
$K_n'=W\mu_n C_{\mathrm{ox}}/(2L)$은 n 채널 MOSFET에서 전도 파라미터(process conduction parameter)라고 하며, 마찬가지로 A/V$^2$의 단위를 사용한다.
포화영역에서 이상적인 $I_D-V_{DS}$ 관계식은 다음과 같이 주어진다. \begin{aligned} &I_D=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left(V_{GS}-V_T\right)^2 \qquad (10.45a)\\[10pt] &I_D=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left(V_{GS}-V_T\right)^2 \qquad (10.45b)\\[10pt] &I_D=K_n\left(V_{GS}-V_T\right)^2 \qquad (10.45c) \end{aligned} 위 식으로부터 $I_D$는 $W$와 $L$값에 의해 조절될 수 있음을 알수있다.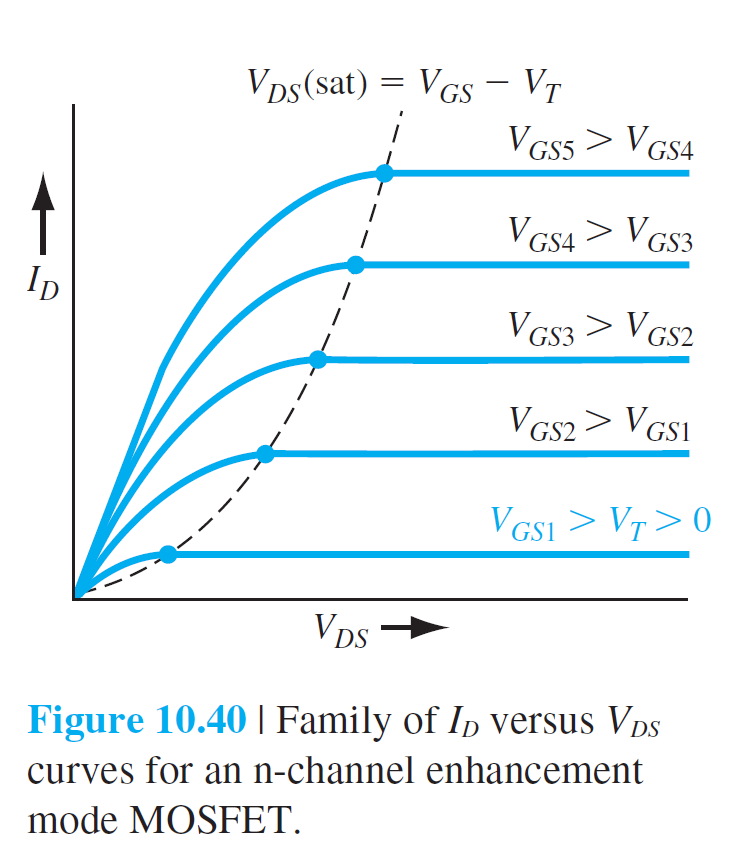

$V_{DS}$는 source와 drain사이에 걸린 전압을 의미하며, 이것이 매우 작을때는 아래와 같은 $I_D$와 다음과 같은 선형 관계를 가진다고 할수있다. $$ I_D=g_d V_{DS} \qquad (10.41) $$ 여기서 $I_D$는 drain으로 흐르는 전류를 의미하고, $g_d$는 다음과 같이 주어지는데 $V_{DS}$가 거의 0일때의 채널 전도도를 의미한다. $$ g_d=\frac{W}{L} \cdot \mu_n\left|Q_n'\right| \qquad (10.42) $$ 여기서 각 기호들의 정의는 다음과 같다.
| 기호 | 의미 |
|---|---|
| $W$ | 채널의 폭 |
| $L$ | 채널의 길이 |
| $\mu_n$ | inversion 층에서 전자의 이동도 |
| $\left|Q_n'\right|$ | 단위 면적당 inversion 층 전하의 크기 |

그림 10.39는 $V_{GS} > V_T$에서 전하분포와 $I_D-V_{DS}$의 전체적인 경향을 보여주고 있다. 각 그림에 대한 상세 설명은 다음과 같다.
• 그림 10.39(a)
$V_{DS}$가 매우 작을 경우에는 $I_D$가 $V_{DS}$에 선형적으로 증가한다. inversion 층의 두께는 전체 채널에 대해서 거의 일정하다.
• 그림 10.39(b)
$V_{DS}$가 좀더 증가하게 되면, source에서 drain 쪽으로 갈수록 채널 영역의 inversion 층의 두께가 감소한다. 이것은 $V_{DS}$로 인하여 채널 영역의 모든 영역에서 포텐셜이 같지 않게 되었기 때문이다. Gate, source, drain이 각각 $V_{G}$, $V_{S}$, $V_{D}$의 포텐셜에 있다면, source 측에서 gate로 부터 느끼는 전압 $V_{SG}$과 drain 측에서 gate로 부터 느끼는 전압 $V_{DG}$는 다른 값을 가지게 된다. 그래서 $V_{DG}$는 $V_{SG}$보다 작은 값을 가질 수 있다. 이러한 방식으로 source에서 drain으로 갈수록 inversion 전자농도가 감소하게 된다. 이 inversion 층 두께의 감소로 인하여 전도도가 감소하는데 이것은 $I_D-V_{DS}$곡선에서 기울기의 감소로 나타난다.
• 그림 10.39(c)
$V_{DS}$가 좀더 증가하게 되어, $V_{DG}$가 $V_T$와 같아지게 되는 조건이 될수있다. 이 경우 drain쪽 채널에 형성된 inversion 전자농도는 0이 된다. 그러면 전도도는 0이 되고, $I_D-V_{DS}$이 기울기는 0이된다. 이러한 상태를 다음 식으로 표현할 수 있다.
\begin{aligned} &V_{G} -V_{D} = V_T \\[10pt] &V_{GS}-V_{DS}(\mathrm{sat})=V_T \qquad (10.43a)\\[10pt] &V_{DS}(\mathrm{sat})=V_{GS}-V_T \qquad (10.43b) \end{aligned} 여기서 $V_{DS}(\mathrm{sat})$는 drain 단자에서 inversion 전자농도가 0이 되는 전압을 의미한다.
• 그림 10.39(d)
$V_{DS} > V_{DS}(\mathrm{sat})$인 상태에서 $V_{DS}$가 계속 증가하면, inversion 전자농도가 0이되는 지점은 source 쪽으로 이동한다. 전자들은 inversion 층에서 전기장에 의해 공핍층을 가로질러 drain 쪽으로 이동을 하게 된다. 이 경우 $I_D$는 $V_{DS}$에 무관하게 일정한 값을 가지게 되는데, 이 영역을 포화영역(saturation region)이라고 한다.

기타자료
비포화영역에서 $I_D-V_{DS}$ 그래프는 다음과 같이 주어진다. $$ I_D=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44a) $$ 위 식은 다음과 같이 쓸수있다. $$ \begin{aligned} I_D&=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44b)\\[10pt] I_D&=K_n\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.44c) \end{aligned} $$ $k_n'=\mu_n C_{\mathrm{ox}}$는 n 채널 MOSFET에서 공정 전도 파라미터(process conduction parameter)라고 하며, A/V$^2$의 단위를 사용한다.
$K_n'=W\mu_n C_{\mathrm{ox}}/(2L)$은 n 채널 MOSFET에서 전도 파라미터(process conduction parameter)라고 하며, 마찬가지로 A/V$^2$의 단위를 사용한다.
포화영역에서 이상적인 $I_D-V_{DS}$ 관계식은 다음과 같이 주어진다. \begin{aligned} &I_D=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left(V_{GS}-V_T\right)^2 \qquad (10.45a)\\[10pt] &I_D=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left(V_{GS}-V_T\right)^2 \qquad (10.45b)\\[10pt] &I_D=K_n\left(V_{GS}-V_T\right)^2 \qquad (10.45c) \end{aligned} 위 식으로부터 $I_D$는 $W$와 $L$값에 의해 조절될 수 있음을 알수있다.



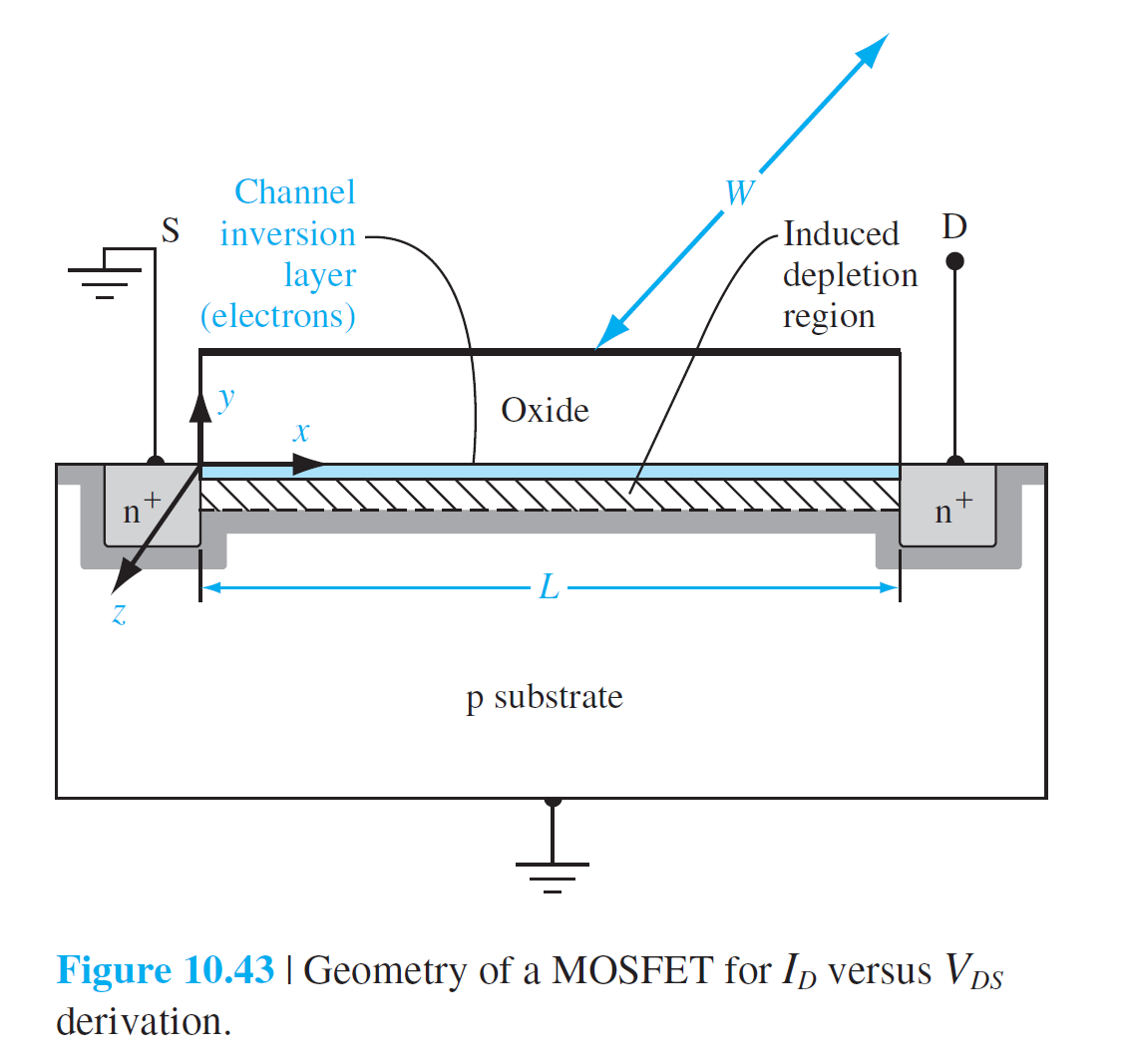
10.3.3 I-V 곡선(수학적 유도)
\begin{equation}
J_x=\sigma E_x \qquad (10.46)
\end{equation}
$$
\begin{aligned}
I_x & =\int_y \int_z J_x d y d z \qquad (10.47)\\[10pt]
Q_n' & =-\int \operatorname{en}(y) d y \qquad (10.48)
\end{aligned}
$$
$$
I_x=-W \mu_n Q_n' E_x \qquad (10.49)
$$
$$
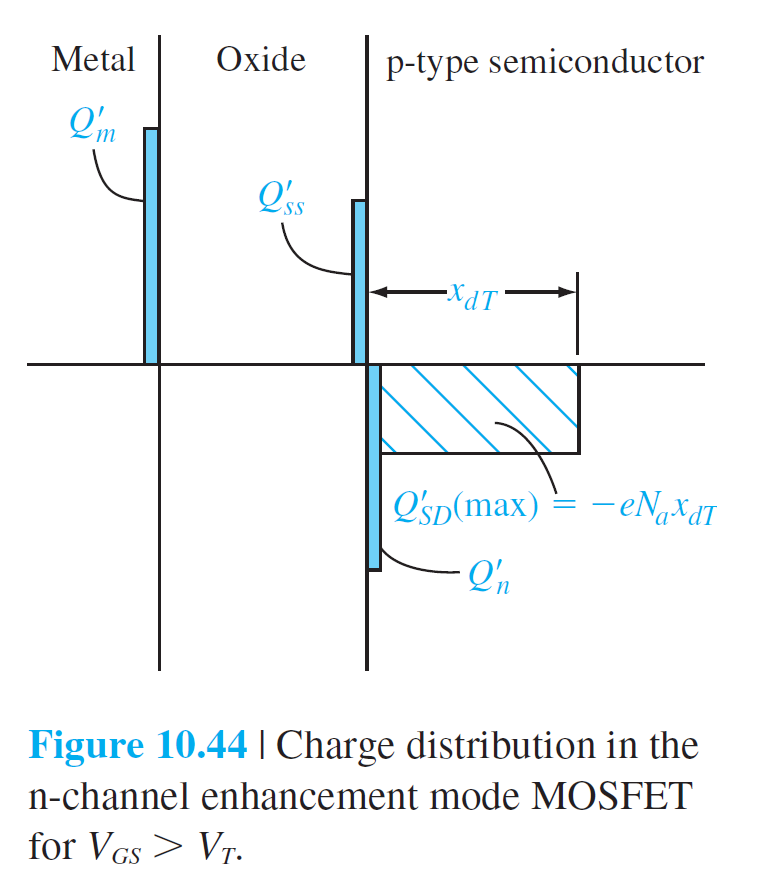
Q_m'+Q_{ss}'+Q_n'+Q_{SD}'(\max )=0 \qquad (10.50)
$$
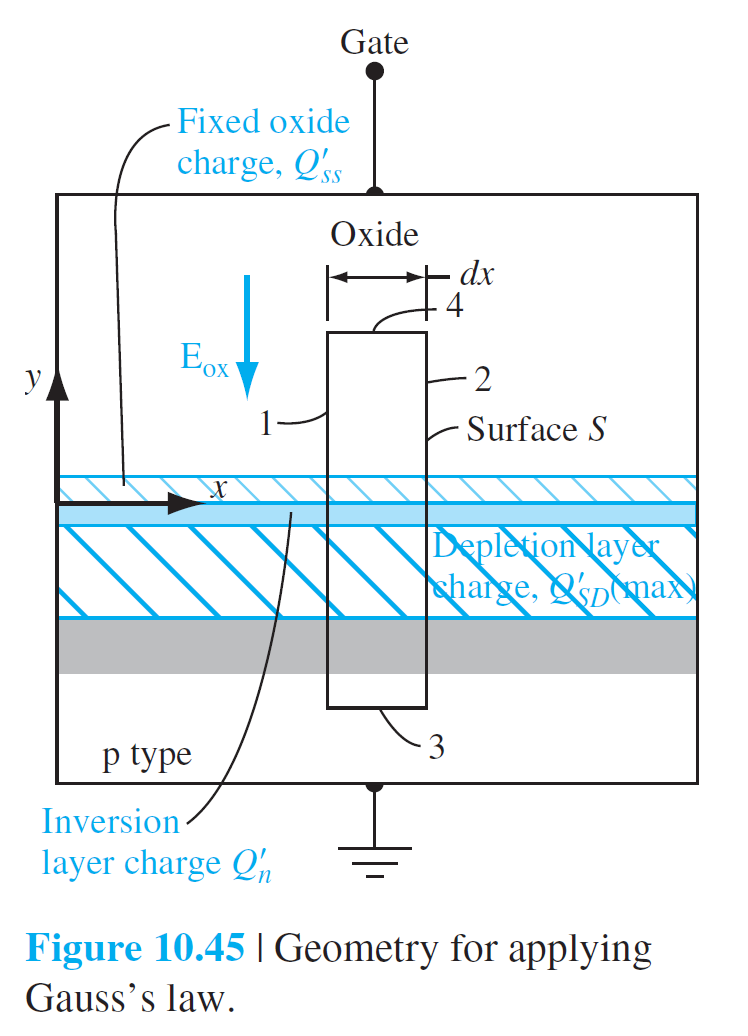
$$
\oint_s \epsilon E_n d S=Q_T \qquad (10.51)
$$
$$
\oint_s \epsilon E_n d S=-\epsilon_{\mathrm{ox}} E_{\mathrm{ox}} W d x=Q_T \qquad (10.52)
$$
$$
Q_T=\left[Q_{ss}'+Q_n'+Q_{SD}'(\max )\right] W d x \qquad (10.53)
$$
$$
-\epsilon_{\mathrm{ox}} E_{\mathrm{ox}}=Q_{ss}'+Q_n'+Q_{SD}'(\max ) \qquad (10.54)
$$
$$
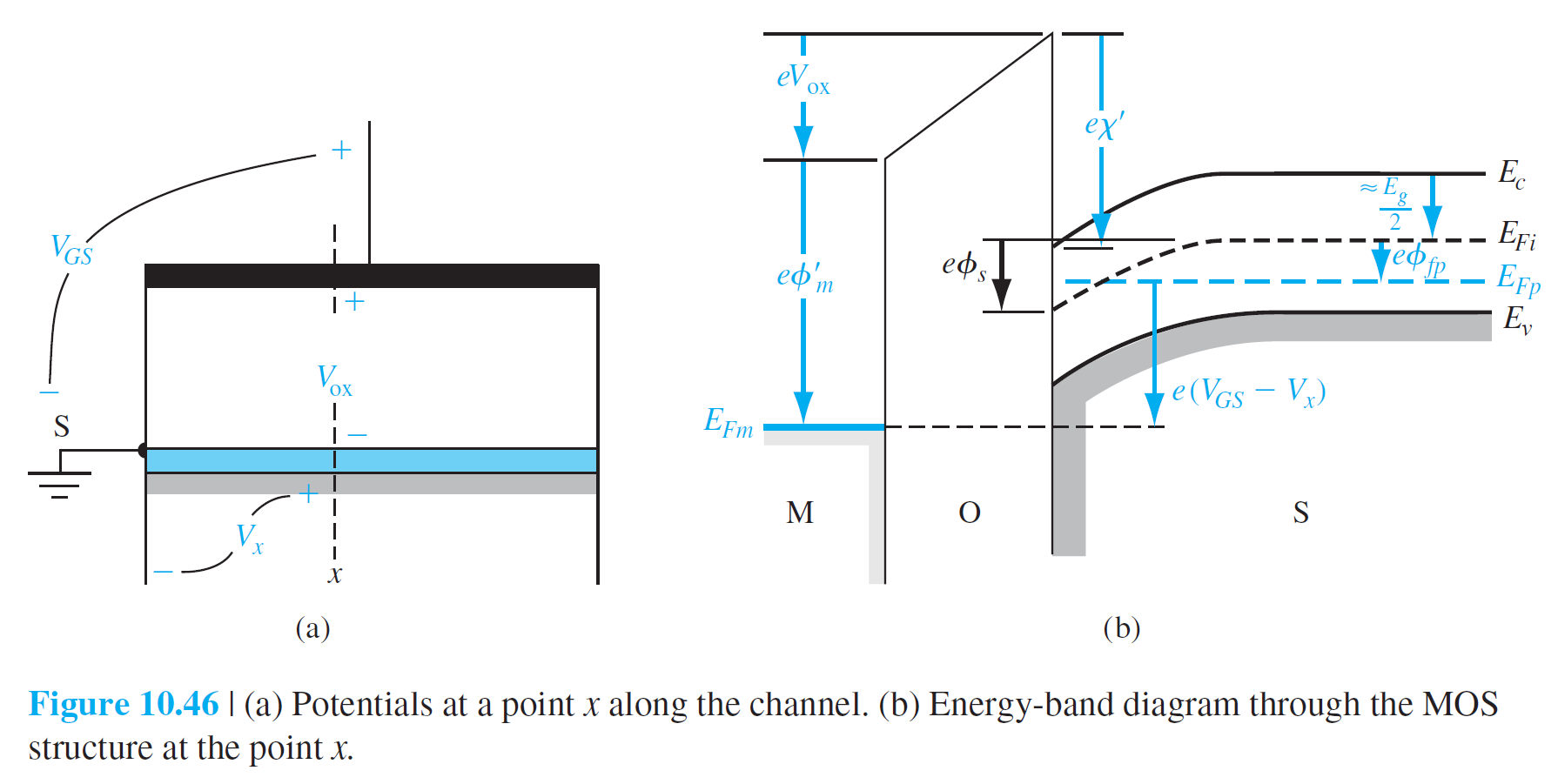
E_{F p}-E_{F m}=e\left(V_{GS}-V_x\right) \qquad (10.54)
$$
$$
V_{GS}-V_x=\left(\phi_m'+V_{\mathrm{ox}}\right)-\left(\chi'+\frac{E_g}{2 e}-\phi_s+\phi_{Fp}\right) \qquad (10.55)
$$
$$
V_{GS}-V_x=V_{\mathrm{ox}}+2 \phi_{Fp}+\phi_{ms} \qquad (10.56)
$$
$$
E_{\mathrm{ox}}=\frac{V_{\mathrm{ox}}}{t_{\mathrm{ox}}} \qquad (10.57)
$$
$$
\begin{aligned}
-\epsilon_{\mathrm{ox}} E_{\mathrm{ox}} & =\frac{-\epsilon_{\mathrm{ox}}}{t_{\mathrm{ox}}}\left[\left(V_{GS}-V_x\right)-\left(\phi_{ms}+2 \phi_{Fp}\right)\right] \qquad (10.58)\\[10pt]
& =Q_{ss}'+Q_n'+Q_{SD}'(\max ) \qquad (10.59)
\end{aligned}
$$
$$
I_x=-W \mu_n C_{\mathrm{ox}} \frac{d V_x}{d x}\left[\left(V_{GS}-V_x\right)-V_T\right] \qquad (10.60)
$$
$$
\int_0^L I_x d x=-W \mu_n C_{\mathrm{ox}} \int_{V_x(0)}^{V_x(L)}\left[\left(V_{GS}-V_T\right)-V_x\right] d V_x \qquad (10.61)
$$
$$
I_D=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.62)
$$
$$
\begin{aligned}
I_D&=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \\[10pt]
&=K_n\left[2\left(V_{GS}-V_T\right) V_{DS}-V_{DS}^2\right] \qquad (10.63)
\end{aligned}
$$
$$
V_{DS}=V_{GS}-V_T \qquad (10.64)
$$
$$
I_D(\mathrm{sat})=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left[2\left(V_{GS}-V_T\right) V_{DS}(\mathrm{sat})-V_{DS}^2(\mathrm{sat})\right]
$$
(10.65)
$$
I_D(\mathrm{sat})=\frac{W \mu_n C_{\mathrm{ox}}}{2 L}\left(V_{GS}-V_T\right)^2 \qquad (10.66)
$$
$$
I_D=\frac{k_n'}{2} \cdot \frac{W}{L} \cdot\left(V_{GS}-V_T\right)^2=K_n\left(V_{GS}-V_T\right)^2 \qquad (10.67)
$$
 \begin{equation}
I_D=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) V_{DS} \qquad (10.68)
\end{equation}
\begin{equation}
\sqrt{I_D(\mathrm{sat})}=\sqrt{\frac{W \mu_n C_{\mathrm{ox}}}{2 L}}\left(V_{GS}-V_T\right) \qquad (10.69)
\end{equation}
\begin{equation}
I_D=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) V_{DS} \qquad (10.68)
\end{equation}
\begin{equation}
\sqrt{I_D(\mathrm{sat})}=\sqrt{\frac{W \mu_n C_{\mathrm{ox}}}{2 L}}\left(V_{GS}-V_T\right) \qquad (10.69)
\end{equation}
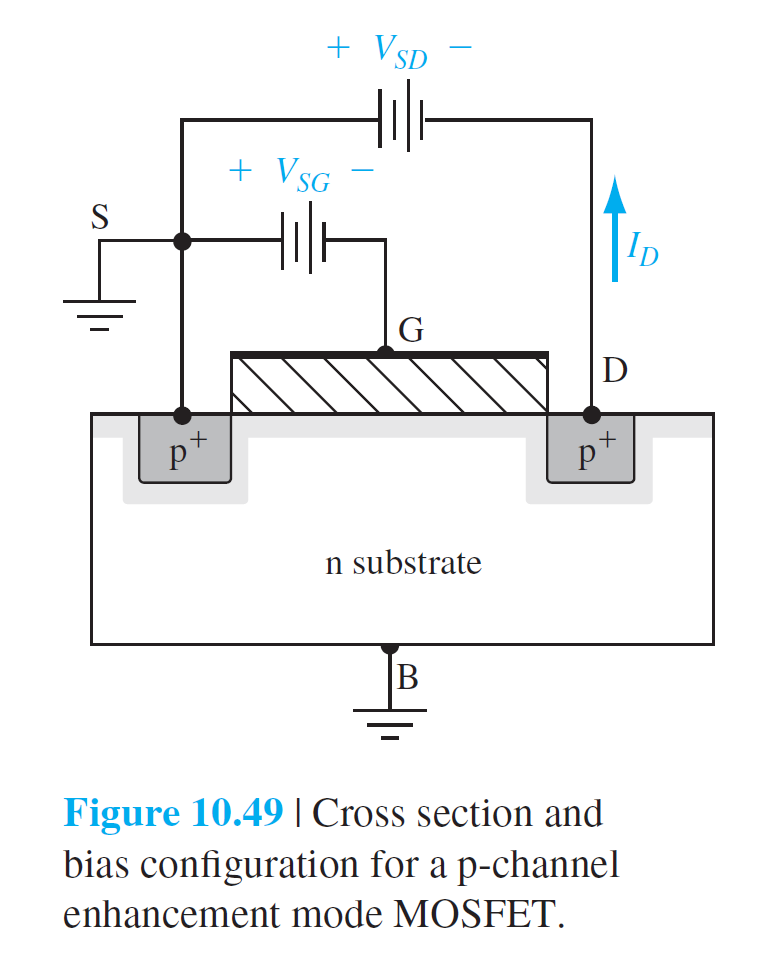
 \begin{equation}
I_D=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.70)
\end{equation}
$$
\begin{aligned}
I_D & =\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \\[10pt]
& =K_p\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.71)
\end{aligned}
$$
$$
I_D(\mathrm{sat})=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left(V_{S G}+V_T\right)^2 \qquad (10.72)
$$
$$
I_D=\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left(V_{S G}+V_T\right)^2=K_p\left(V_{S G}+V_T\right)^2 \qquad (10.73)
$$
$$
V_{SD}(s a t)=V_{S G}+V_T \qquad (10.74)
$$
\begin{equation}
I_D=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.70)
\end{equation}
$$
\begin{aligned}
I_D & =\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \\[10pt]
& =K_p\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.71)
\end{aligned}
$$
$$
I_D(\mathrm{sat})=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left(V_{S G}+V_T\right)^2 \qquad (10.72)
$$
$$
I_D=\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left(V_{S G}+V_T\right)^2=K_p\left(V_{S G}+V_T\right)^2 \qquad (10.73)
$$
$$
V_{SD}(s a t)=V_{S G}+V_T \qquad (10.74)
$$






 \begin{equation}
I_D=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) V_{DS} \qquad (10.68)
\end{equation}
\begin{equation}
\sqrt{I_D(\mathrm{sat})}=\sqrt{\frac{W \mu_n C_{\mathrm{ox}}}{2 L}}\left(V_{GS}-V_T\right) \qquad (10.69)
\end{equation}
\begin{equation}
I_D=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) V_{DS} \qquad (10.68)
\end{equation}
\begin{equation}
\sqrt{I_D(\mathrm{sat})}=\sqrt{\frac{W \mu_n C_{\mathrm{ox}}}{2 L}}\left(V_{GS}-V_T\right) \qquad (10.69)
\end{equation}
 \begin{equation}
I_D=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.70)
\end{equation}
$$
\begin{aligned}
I_D & =\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \\[10pt]
& =K_p\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.71)
\end{aligned}
$$
$$
I_D(\mathrm{sat})=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left(V_{S G}+V_T\right)^2 \qquad (10.72)
$$
$$
I_D=\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left(V_{S G}+V_T\right)^2=K_p\left(V_{S G}+V_T\right)^2 \qquad (10.73)
$$
$$
V_{SD}(s a t)=V_{S G}+V_T \qquad (10.74)
$$
\begin{equation}
I_D=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.70)
\end{equation}
$$
\begin{aligned}
I_D & =\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \\[10pt]
& =K_p\left[2\left(V_{S G}+V_T\right) V_{SD}-V_{SD}^2\right] \qquad (10.71)
\end{aligned}
$$
$$
I_D(\mathrm{sat})=\frac{W \mu_p C_{\mathrm{ox}}}{2 L}\left(V_{S G}+V_T\right)^2 \qquad (10.72)
$$
$$
I_D=\frac{k_p'}{2} \cdot \frac{W}{L} \cdot\left(V_{S G}+V_T\right)^2=K_p\left(V_{S G}+V_T\right)^2 \qquad (10.73)
$$
$$
V_{SD}(s a t)=V_{S G}+V_T \qquad (10.74)
$$



10.3.4 전달 전도도
$$
g_m=\frac{\partial I_D}{\partial V_{GS}} \qquad (10.75)
$$
$$
g_{m L}=\frac{\partial I_D}{\partial V_{GS}}=\frac{W \mu_n C_{\mathrm{ox}}}{L} \cdot V_{DS} \qquad (10.76)
$$
$$
g_{ms}=\frac{\partial I_D(\mathrm{sat})}{\partial V_{GS}}=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) \qquad (10.77)
$$
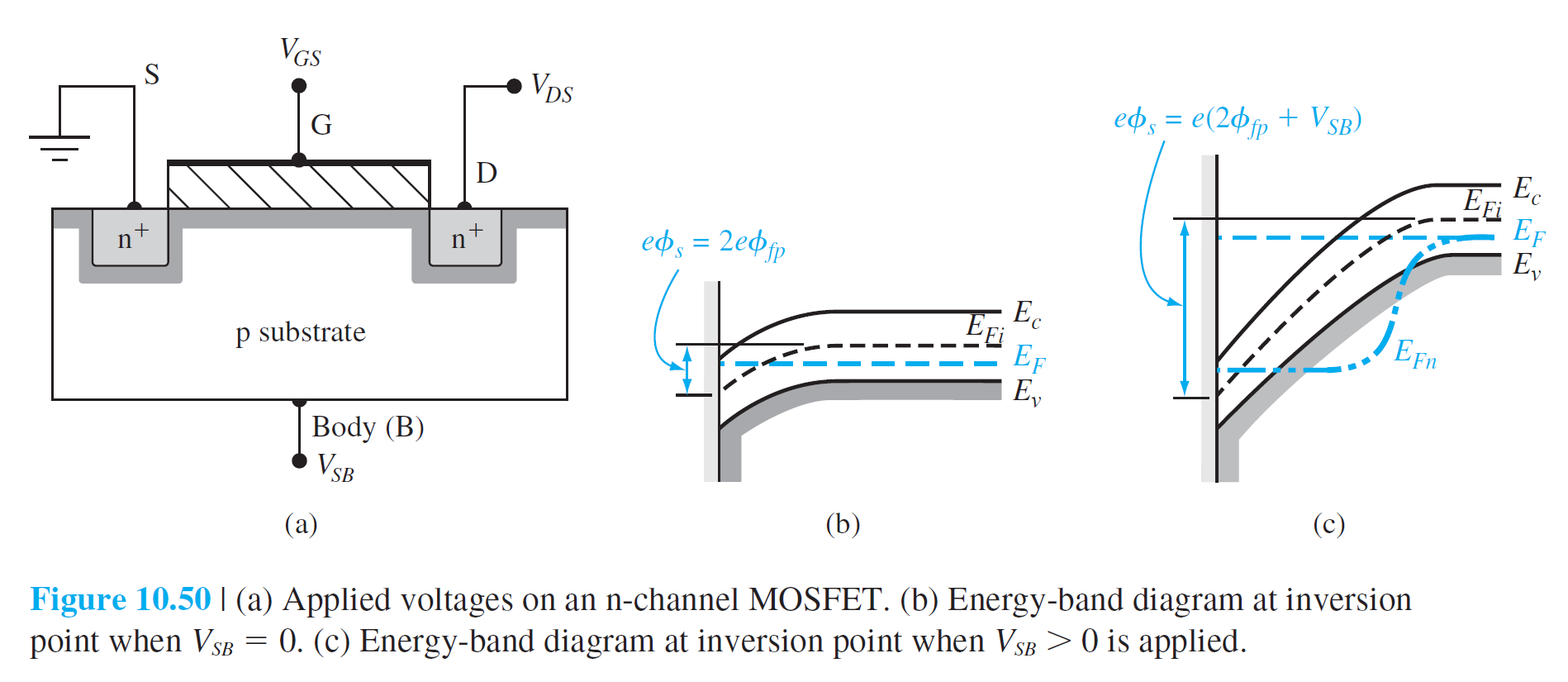
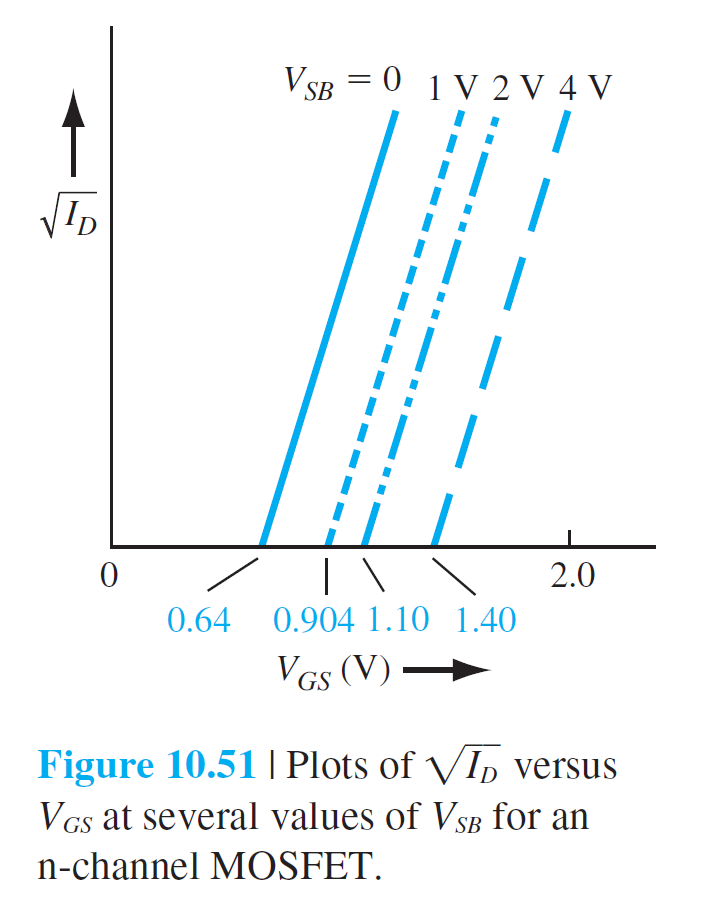
10.3.5 기판 전위 효과
$$
Q_{SD}'(\max )=-e N_a x_{dT}=-\sqrt{2 e \epsilon_s N_a\left(2 \phi_{Fp}\right)} \qquad (10.78)
$$
$$
Q_{SD}'=-e N_a x_d=-\sqrt{2 e \epsilon_s N_a\left(2 \phi_{Fp}+V_{S B}\right)} \qquad (10.79)
$$
$$
\Delta Q_{SD}'=-\sqrt{2 e \epsilon_s N_a}\left[\sqrt{2 \phi_{Fp}+V_{S B}}-\sqrt{2 \phi_{Fp}}\right] \qquad (10.80)
$$
$$
\Delta V_T=-\frac{\Delta Q_{SD}'}{C_{\mathrm{ox}}}=\frac{\sqrt{2 e \epsilon_s N_a}}{C_{\mathrm{ox}}}\left[\sqrt{2 \phi_{Fp}+V_{S B}}-\sqrt{2 \phi_{Fp}}\right]
$$
(10.81)
$$
\gamma=\frac{\sqrt{2 e \epsilon_s N_a}}{C_{\mathrm{ox}}} \qquad (10.82)
$$
$$
\Delta V_T=\gamma\left[\sqrt{2 \phi_{Fp}+V_{S B}}-\sqrt{2 \phi_{Fp}}\right] \qquad (10.83)
$$




10.4 주파수 제한
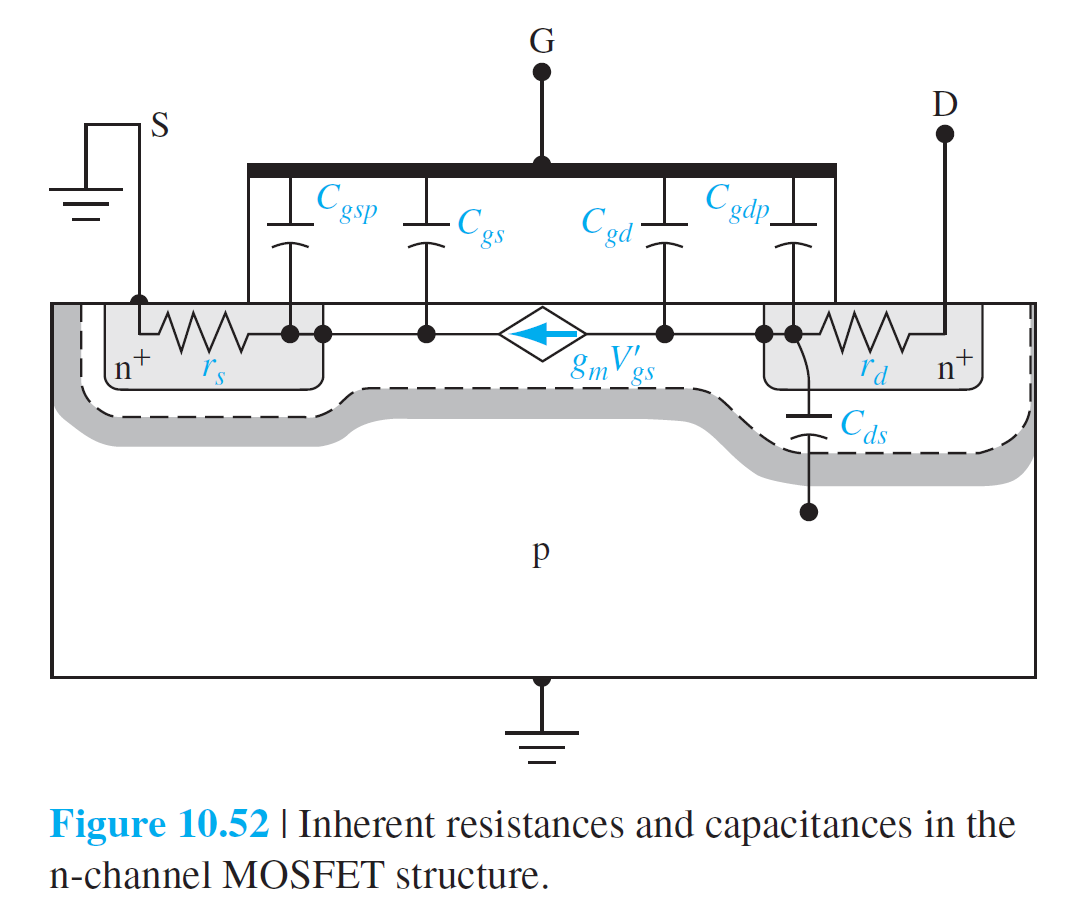
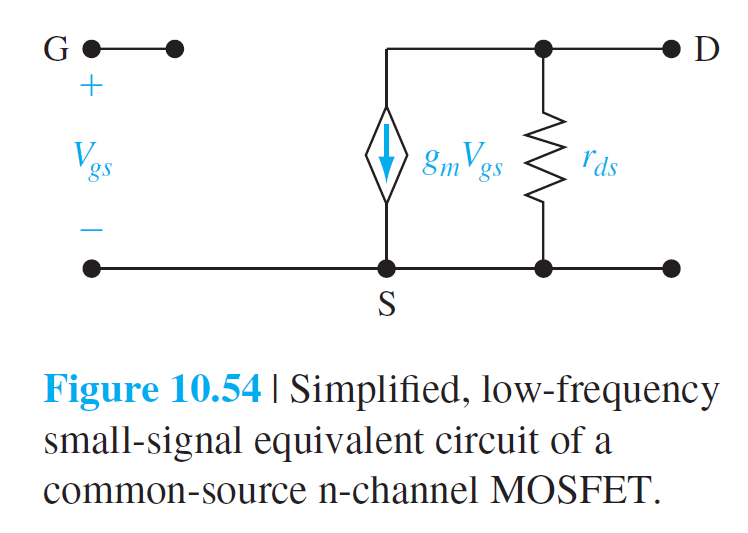
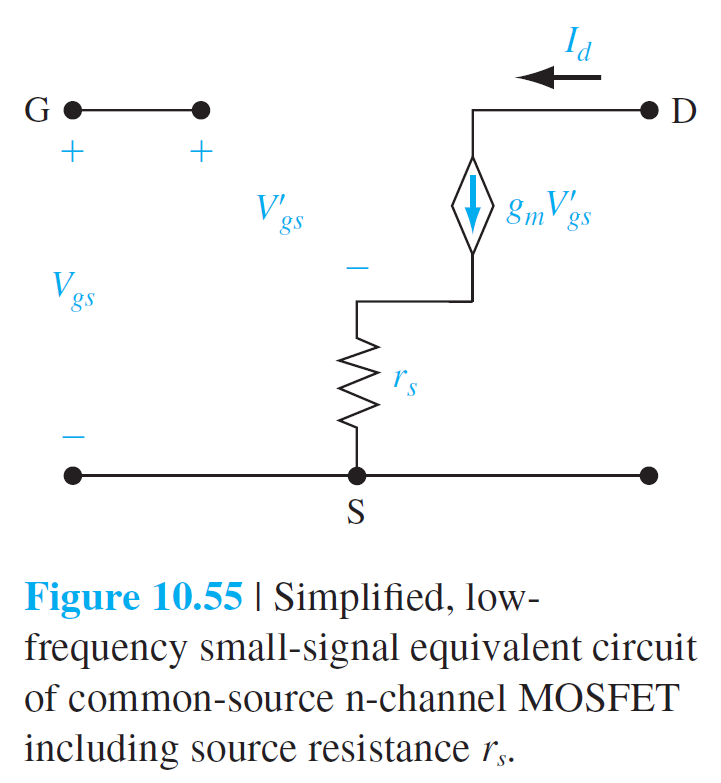
10.4.1 소신호 등가회로
$$
I_d=g_m V_{gs}' \qquad (10.84)
$$
$$
V_{gs}=V_{gs}'+\left(g_m V_{gs}'\right) r_s=\left(1+g_m r_s\right) V_{gs}' \qquad (10.85)
$$
$$
I_d=\left(\frac{g_m}{1+g_m r_s}\right) V_{gs}=g_m' V_{gs} \qquad (10.86)
$$
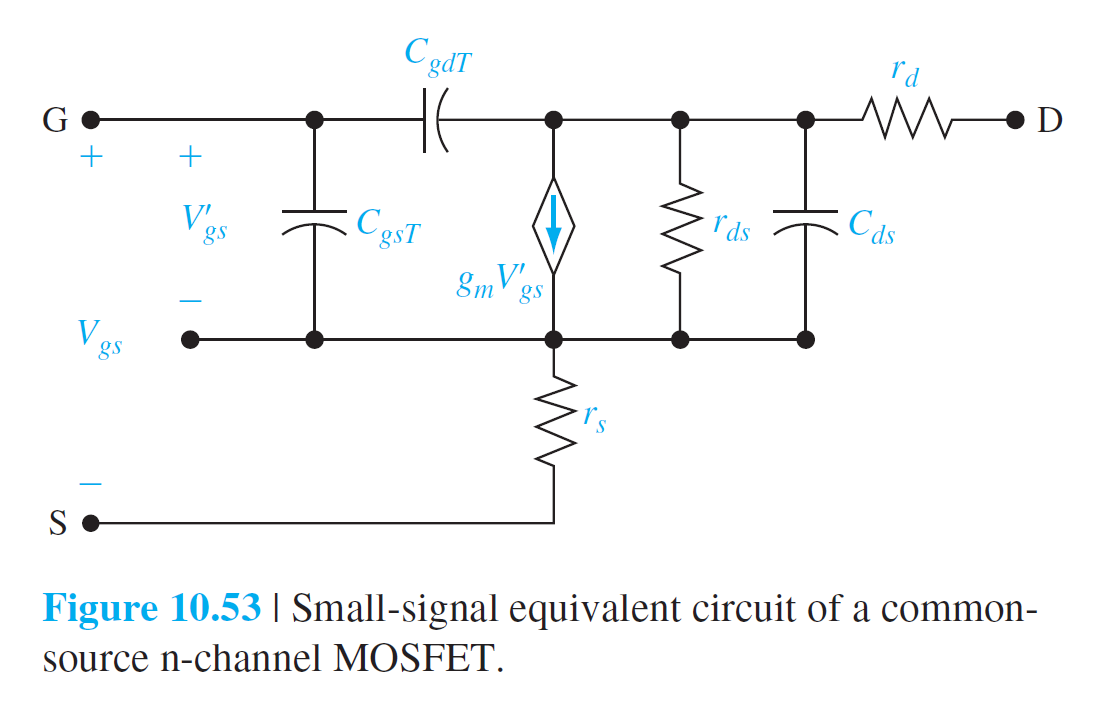




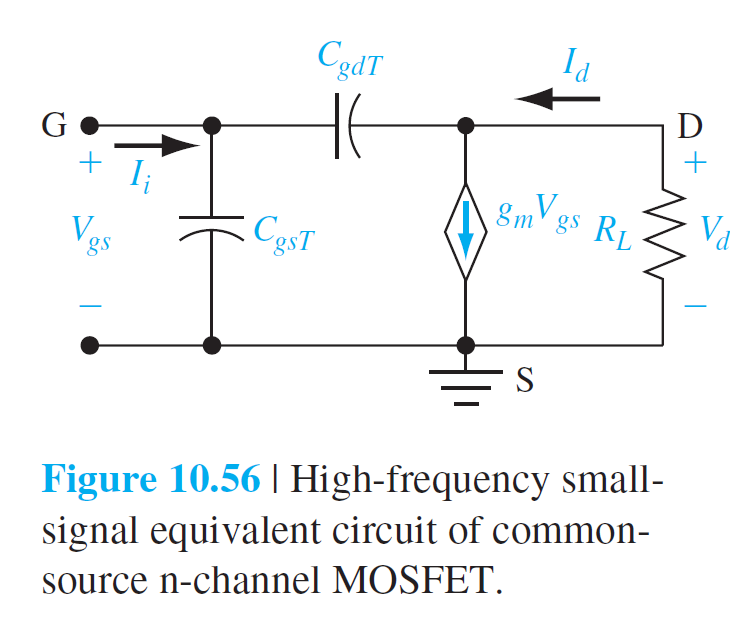
10.4.2 주파수 제한 요소와 차단 진동수
$$
I_i=j \omega C_{gsT} V_{gs}+j \omega C_{gdT}\left(V_{gs}-V_d\right) \qquad (10.87)
$$
$$
\frac{V_d}{R_L}+g_m V_{gs}+j \omega C_{gdT}\left(V_d-V_{gs}\right)=0 \qquad (10.88)
$$
$$
I_i=j \omega\left[C_{gsT}+C_{gdT}\left(\frac{1+g_m R_L}{1+j \omega R_L C_{gdT}}\right)\right] V_{gs} \qquad (10.89)
$$
$$
I_i=j \omega\left[C_{gsT}+C_{gdT}\left(1+g_m R_L\right)\right] V_{gs} \qquad (10.90)
$$
$$
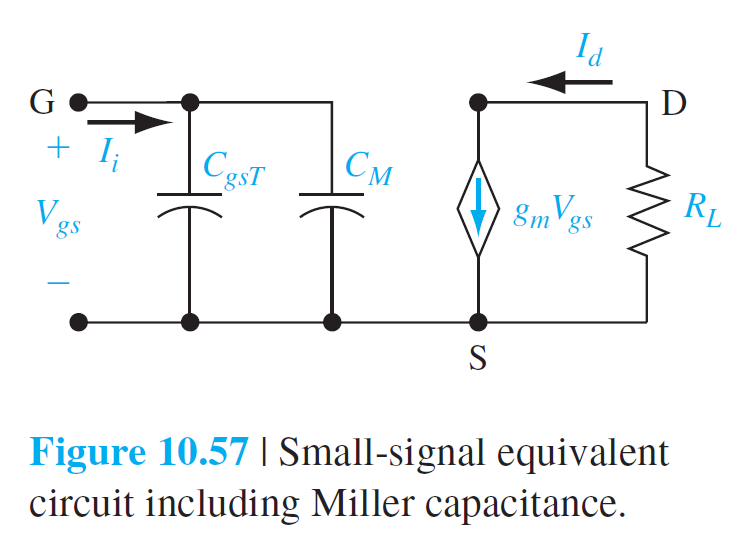
C_M=C_{gdT}\left(1+g_m R_L\right) \qquad (10.91)
$$
$$
I_i=j \omega\left(C_{gsT}+C_M\right) V_{gs} \qquad (10.92)
$$
$$
I_d=g_m V_{gs} \qquad (10.93)
$$
$$
\left|\frac{I_d}{I_i}\right|=\frac{g_m}{2 \pi f\left(C_{gsT}+C_M\right)} \qquad (10.94)
$$
$$
f_T=\frac{g_m}{2 \pi\left(C_{gsT}+C_M\right)}=\frac{g_m}{2 \pi C_G} \qquad (10.95)
$$
$$
g_{ms}=\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right) \qquad (10.96)
$$
$$
f_T=\frac{g_m}{2 \pi C_G}=\frac{\frac{W \mu_n C_{\mathrm{ox}}}{L}\left(V_{GS}-V_T\right)}{2 \pi\left(C_{\mathrm{ox}} W L\right)}=\frac{\mu_n\left(V_{GS}-V_T\right)}{2 \pi L^2}
$$




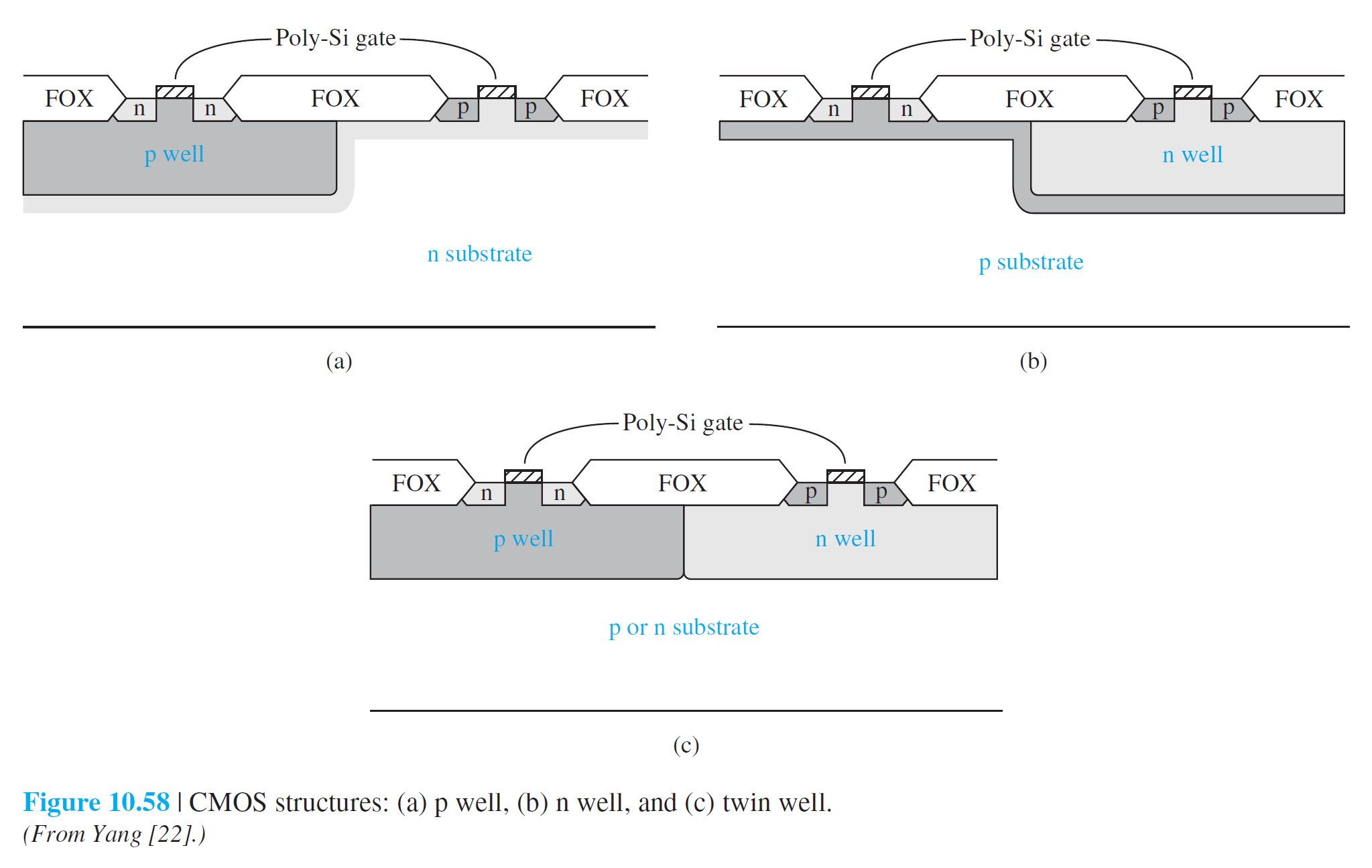
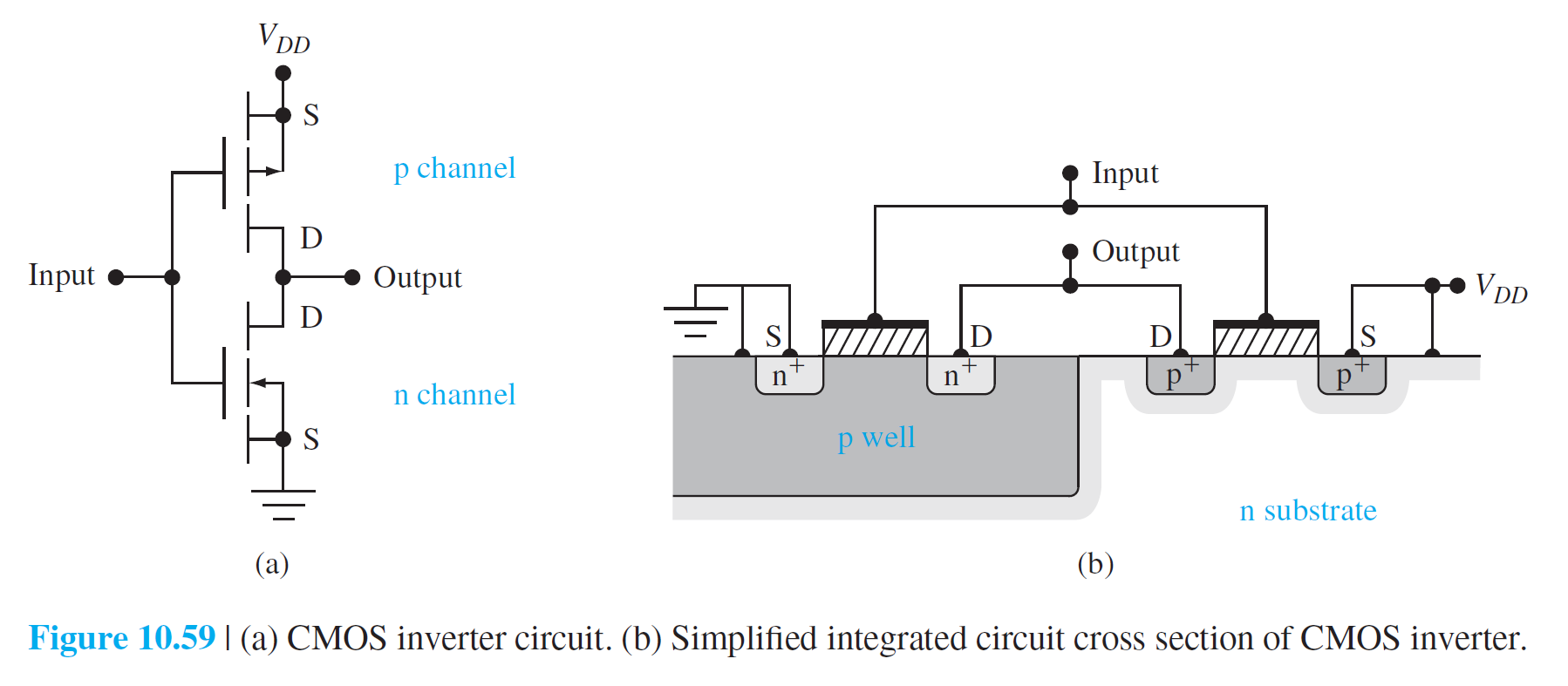
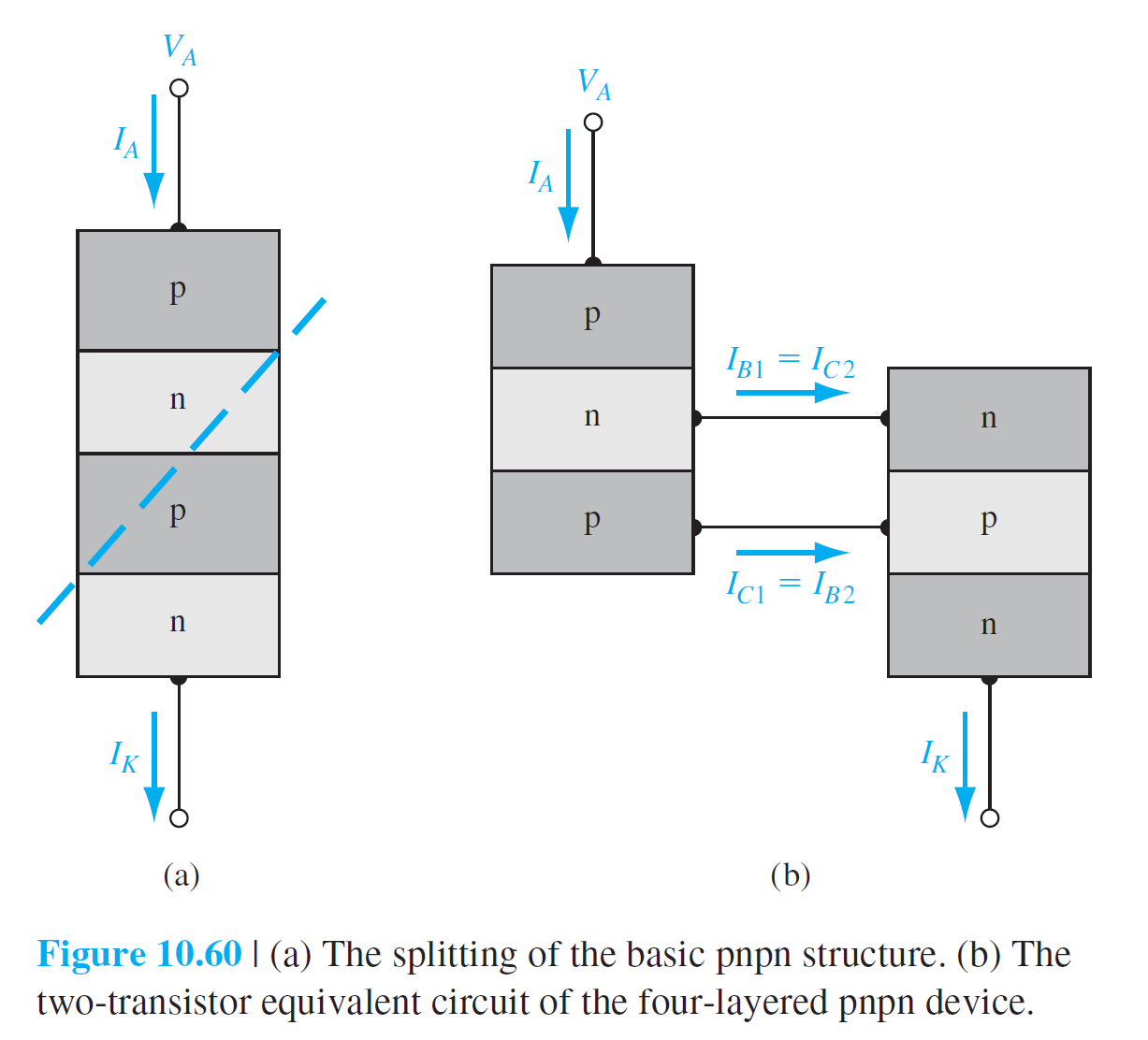
10.4.3 CMOS 기술