10. 자기에너지

본 장에서는 자기장에 저장된 에너지를 구해보고자 한다. 그러기 위해서 우선 회로 분석으로부터 자기장과 에너지 사이의 관계를 연구해보자.

10.1 회로의 자기에너지

• 단일회로에 저장된 에너지

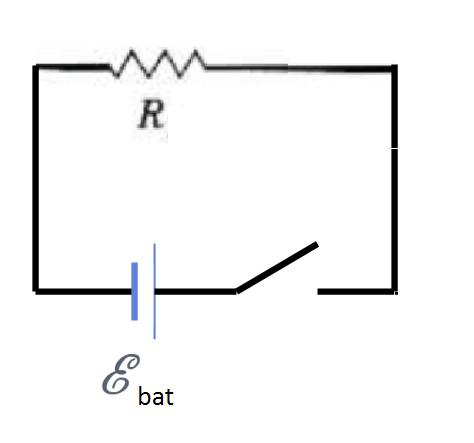
그림과 같은 단순한 저항 회로를 생각해 보자. 스위치가 닫으면 회로 방정식은 다음과 같이 될것이라고 생각할 수 있다. $$ \mathscr{E}_{bat} - I R=0 $$ 여기서 $I$는 회로가 정적 상태라고 가정될 때의 전류이다.
그러나 엄밀하게는 스위치를 닫는 순간 곧바로 전류가 정적상태의 값 $I$를 갖는 것은 아니다. 왜냐하면 회로를 통과하는 자기다발을 현상유지 하려는 성질때문에 스위치를 닫는 순간 잠시나마 유도 기전력이 발생하여, 전류는 0에서 최종값 $I$까지 약간의 시간을 두고 도달한다. 이 과정에서 이 유도 기전력에 의한 전류는 저항에 의하여 사라진다. 비록 유도 기전력이 한 일은 저항에 의해 열에너지로 다 흩어졌지만, 결과적으로보면 회로에 저장된 에너지는 이 유도 기전력이 한 일과 동일하다고 볼수있다. 회로에 저장된 에너지는 회로가 형성되는데 투입된 에너지 또는 회로가 형성되면서 만들어진 자기장에 저장된 에너지로도 볼수있다. 유도 기전력까지 포함된 회로 방정식은 다음과 같이 주어진다. $$ \mathscr{E}_{bat}+\mathscr{E}_{ind}-I R=0 $$ 6장에 의하면 전력(일률)은 $P=IV$로 주어진다. 저항 양단에 전압강하 $V$에 의해 단위시간당 소실되는 에너지를 의미한다. 이 표현과 유사하게 유도 기전력에 의해 단위시간당 획득하는 에너지(한일)는 다음과 같이 주어질 수 있다. $$P=i\mathscr{E}_{ind}$$ 여기서 $i$는 스위치를 닫은 직후 전류가 0에서 $I$에 도달하기 전 중간 시점에서의 전류이다.
위 식을 좀더 전개하면 $$P=i\frac{d\Phi}{dt} = i\frac{d\Phi}{di}\frac{di}{dt} = L i\frac{di}{dt}$$ 그러면 시간 $dt$당 한 일 다음과 같고 $$ dW=P dt = L i di$$ 전류 $i$가 0부터 $I$까지 도달하는데 까지 유도 기전력이 한 총 일은 다음과 같다. $$W =\int_0^I L i di = \frac{1}{2} L I^2$$ 회로에 저장된 에너지는 다음과 같다. $$U = \frac{1}{2} L I^2$$ 자기다발($L=\Phi/I$)에 대한 표현으로 다시 쓰면 $$U = \frac{1}{2} L I^2 = \frac{1}{2} I\Phi = \frac{\Phi^2}{2I}$$ • 다중회로에 저장된 에너지
만약 두 개의 회로가 있다면 저장된 에너지는 다음과 같이 주어질 것이다. \begin{equation} \begin{aligned} U &=\frac{1}{2} L_1 I_1^2 + \frac{1}{2} L_2 I_2^2 + \frac{1}{2} M_{12} I_1 I_2 + \frac{1}{2} M_{21} I_2 I_2 \\ &=\frac{1}{2} L_1 I_1^2 + \frac{1}{2} L_2 I_2^2 + M I_1 I_2 \end{aligned} \end{equation} 자기에너지는 항상 0보다 크거나 같다. $$ U=\frac{1}{2} I_2^2\left(L_1 x^2+2 M x+L_2\right) \geq 0 . $$ 참고로 $I_1/I_2 =x$로 두고 자기에너지 $U$를 최소로 만드는 조건은 다음과 같다. $$ x=-\frac{M}{L_1} $$ 이 조건을 에너지에 대입하여 다음의 최소에너지를 얻는다. $$ \frac{M^2}{L_1}-\frac{2 M^2}{L_1}+L_2 \geq 0 $$ 위 식으로 부터 다음식을 얻는다. $$ L_1 L_2 \geq M^2 $$ 만약 $N$ 개의 회로가 있다면 저장된 에너지는 다음과 같이 주어질 것이다. $$ \begin{aligned} U &= \frac{1}{2} \sum_{i=1}^N I_i \Phi_i \\ &= \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N M_{i j} I_i I_j \\ &= \frac{1}{2} L_1 I_1^2+\frac{1}{2} L_2 I_2^2 + \cdots + \frac{1}{2} L_N I_N^2 \\ & +M_{12} I_1 I_2 + M_{13} I_1 I_3+\cdots+M_{1 N} I_1 I_N \\ & +M_{23} I_2 I_3 + \cdots + M_{N-1, N} I_{N-1} I_N \end{aligned} $$

10.2 자기에너지 밀도

$i$번째 회로를 통과하는 자기다발은 다음과 같다. $$ \Phi_i=\int_{s_i} \vec{B} \cdot \hat{n} d a=\oint_{c_i} \vec{A} \cdot d \vec{\ell}_i, $$ 그러면 다중회로에 저장된 에너지는 다음과 같다. $$ U=\frac{1}{2} \sum_i \oint_{C_i} I_i \vec{A} \cdot d \vec{\ell}_i . $$ $\sum_i \oint_{c_i}$ 대신 $\int_V$으로 바꾸면 $$ U=\frac{1}{2} \int_{V} \vec{J} \cdot \vec{A} d v =\frac{1}{2} \int_{V} (\nabla \times \vec{H}) \cdot \vec{A} d v $$ 다음 관계식에 의하여, $$ \nabla \cdot(\vec{A} \times \vec{H})=\vec{H} \cdot \nabla \times \vec{A}-\vec{A} \cdot \nabla \times \vec{H} $$ $$ U=\frac{1}{2} \int_V \vec{H} \cdot \nabla \times \vec{A} d v-\frac{1}{2} \int_S \vec{A} \times \vec{H} \cdot \hat{n} d a $$ 위 식 우변의 두번째 항 면적분은 매우 크게 잡으면, 사라진다. 결과적으로 다음이 성립한다. $$ U=\frac{1}{2} \int_V \vec{H} \cdot \vec{B} d v $$ 여기서 자기에너지 밀도($u$)를 다음과 같이 정의할 수 있다. $$ u=\frac{1}{2} \vec{H} \cdot \vec{B} $$ $$ u=\frac{1}{2} \mu H^2=\frac{1}{2} \frac{B^2}{\mu} . $$

10.3 힘과 회전력

어떤 회로가 건전지를 포함하고 있을 때, 이 회로의 자기에너지에 영향을 줄수있는 외부요소가 한 일은 다음과 같이 표현될 수 있다. $$ d W = d W_b - d U, $$ 여기서 $d U$는 자기에너지의 변화량, $d W_b$는 건전지가 한 일의 변화량이다. 위 식에서 $W_b$에 대한 표현을 제거하기 위해 다음 식들을 이용하면, $$ \begin{gathered} d U=\frac{1}{2} \sum_i I_i d \Phi_i \\ d W_b=\sum_i I_i d \Phi_i \end{gathered} $$ 다음 표현을 얻게 되고 $$ d W_b=2 d U $$ 결과적으로 외부 요소가 주는 힘은 다음과 같이 주어진다. $$ dW = \vec{F} \cdot d \vec{r} = dU $$ $$ \begin{aligned} \vec{F} & =\nabla U \\ F_x & =\left(\frac{\partial U}{\partial x}\right)_I \end{aligned} $$ 위에서 아래첨자 $I$는 전류가 일정하게 유지된다는 뜻이다. 외부요소가 주는 회전력은 다음과 같이 얻어진다. $$ d W= \vec{\tau} \cdot d \vec{\theta} =\tau_1 d \theta_1+\tau_2 d \theta_2+\tau_3 d \theta_3, $$ $$ \tau_1=\left(\frac{\partial U}{\partial \theta_1}\right)_1 $$ 만약 회로에 건전지가 없다면, 외부요소에 대항해서 회로가 한 일과 회전력은 다음과 같이 표현될 수 있다. $$ \begin{aligned} \vec{F} \cdot d \vec{r} & =d W=-d U \\ F_x & =-\left(\frac{\partial U}{\partial x}\right)_{\Phi} \\ \tau_1 & =-\left(\frac{\partial U}{\partial \theta_1}\right)_{\Phi} \end{aligned} $$ • 예제

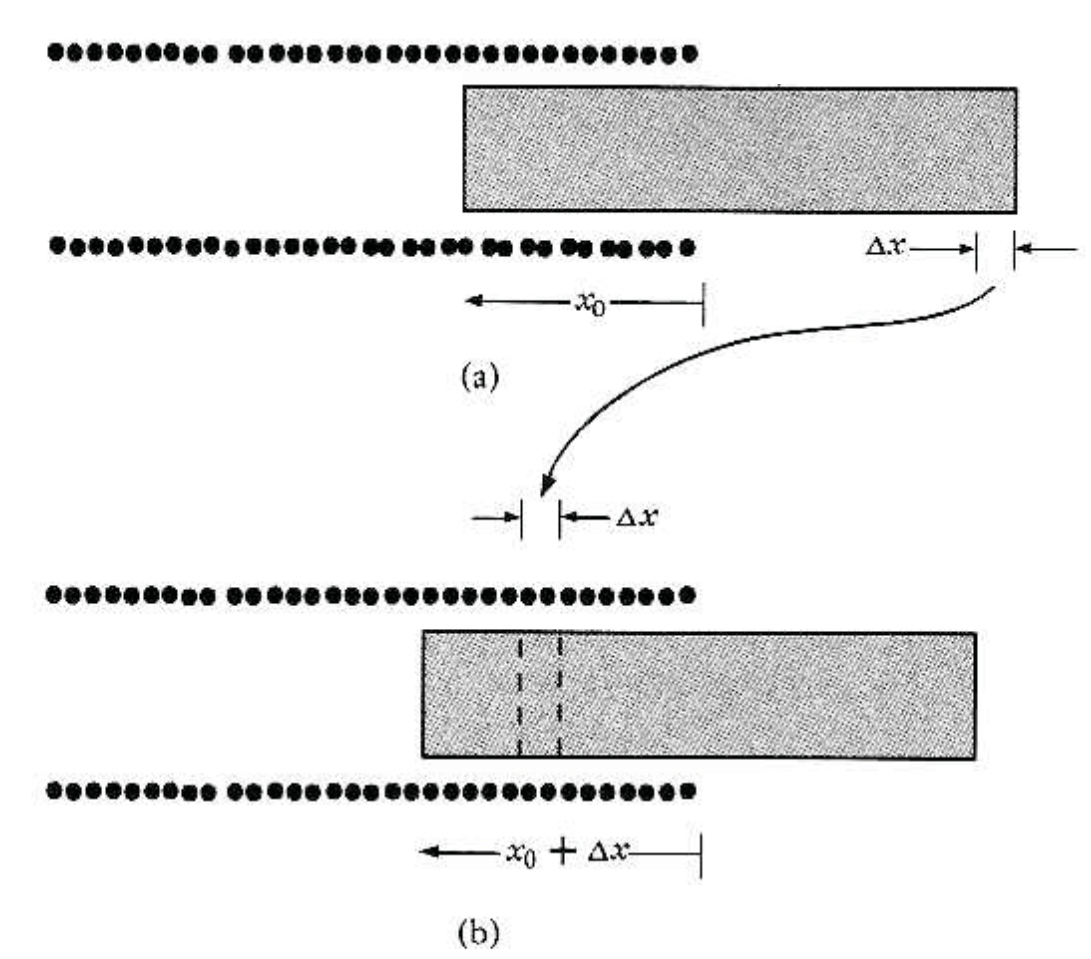
그림과 같이 전류 $I$가 흐르는 솔레노이드에 투자율 $\mu$, 단면적이 $A$인 쇠막대가 완전히 삽입되어있다고 하자. 쇠막대를 절반정도 밖으로 끄집어 내었을 때, 쇠막대를 다시 안으로 끌어당겨지는 힘을 구하자. 다음의 자기에너지 식을 이용하자.
$$ U=\frac{1}{2} \int \mu H^2 d v $$ 쇠막대가 위치 $x_0$와 $x_0+\Delta x$에 있을 때, 자기에너지 차이는 다음과 같이 주어진다. $$ \begin{aligned} U\left(x_0+\Delta x\right) & \approx U\left(x_0\right)+\frac{1}{2} \int_{A \Delta x}\left(\mu-\mu_0\right) H^2 d v \\ & =U\left(x_0\right)+\frac{1}{2}\left(\mu-\mu_0\right) \frac{N^2 I^2}{l^2} A \Delta x \end{aligned} $$ 그러면 $x$방향으로의 힘은 다음과 같이 주어진다. $$ F_x \approx \frac{1}{2}\left(\mu-\mu_0\right) \frac{N^2 I^2 A}{l^2}=\frac{1}{2} \chi_m \mu_0 H^2 A . $$ 여기서 $N I/l = H$ 이다(7.5절 참조).

10.4 이력손실(hysteresis loss)

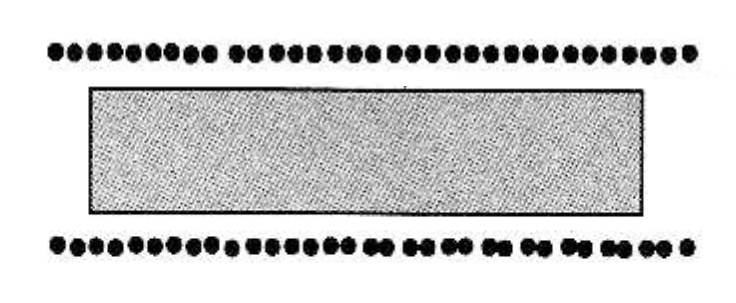
$$ \delta W_b=N I \delta \Phi $$ $$ \delta W_b=\oint \delta \Phi \vec{H} \cdot d \vec{\ell}=\oint A \delta B \vec{H} \cdot d \vec{\ell}, $$ $$ \delta W_b=\oint A \delta \vec{B} \cdot \vec{H} d l=\int_V \delta \vec{B} \cdot \vec{H} d v, $$ $$ d w_b=\vec{H} \cdot d \vec{B} $$ $$ \left(w_b\right)_{a b}=\int_a^b H d B $$ $$ w_b=\oint H d B, $$ $$ d w_b=\vec{H} \cdot d \vec{B}=\mu_0 H d H+\mu_0 \vec{H} \cdot d \vec{M} . $$ $$ w_b=\mu_0 \oint H d M $$ $$ w_b=-\mu_0 \oint M d H $$