11. 교류회로
느리게 흐르는 전류
\begin{equation}
L_{max} \ll \frac{2 \pi c}{\omega} \quad \text { or } \quad \omega \ll \frac{2 \pi c}{L_{max}} .
\end{equation}
\begin{equation}
\begin{array}{lccc}
f(\mathrm{~Hz}) & \omega(\mathrm{rad} / \mathrm{s}) & \lambda(\mathrm{m}) & l_{\text {max }}(\mathrm{m}) \\
\hline \hline 60 & 376 & 5 \times 10^6 & 5 \times 10^5(300 \text { millas }) \\
10^6 & 6.28 \times 10^6 & 300 & 30 \\
10^8 & 6.28 \times 10^8 & 3 & 0.3 \\
10^{10} & 6.28 \times 10^{10} & 0.03 & 0.003
\end{array}
\end{equation}
11.1 Kirchhoff의 법칙
기존의 정적 전류 회로에서의 Kirchhoff의 법칙은 다음과 같다.1. 분기점을 향해 흐르는 전류의 대수적 합은 0이다.
$$ \sum I_j=0 . $$ 2. 회로의 모든 루프의 전압 차이의 대수적 합은 0이다.
$$ \sum V_j=0 . $$ 순간전류일 경우 Kirchhoff의 법칙은 다음과 같다.
1. 분기점을 향해 흐르는 순간 전류의 대수적 합은 0입니다.
2. 닫힌 회로에서 순간 인가 전압의 대수적 합은 회로에서 순간 전압의 대수적 합과 같다.
11.2 회로의 일시적 거동
• R-C 회로
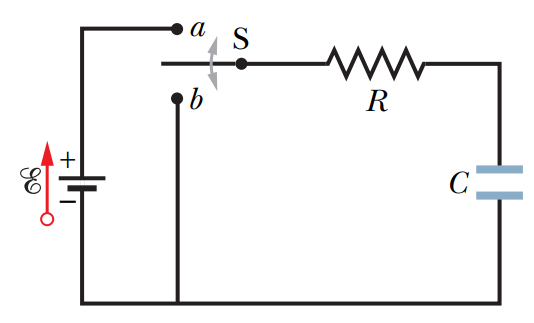
$$
\mathscr{E}-i R-\frac{q}{C}=0 .
$$
$$
i=\frac{d q}{d t} .
$$
$$
R \frac{d q}{d t}+\frac{q}{C}=\mathscr{E}
$$
$$
q=C \mathscr{E} \left(1-e^{-t / R C}\right)
$$
\begin{equation}
i=\frac{d q}{d t}=\left(\frac{\mathscr{E}}{R}\right) e^{-t / R C}
\end{equation}
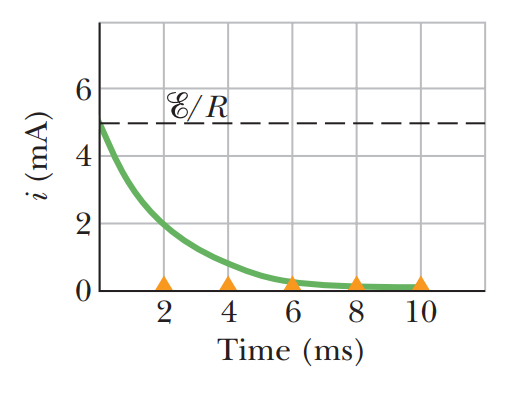
• R-L-C 회로

$$
Q=\int_{t_0}^t I(t) d t
$$
$$
\mathscr{E}=R I+L \frac{d I}{d t}+\frac{1}{C} \int_{t_0}^t I(t) d t
$$
$$
\frac{d \mathscr{E}}{d t}=R \frac{d I}{d t}+L \frac{d^2 I}{d t^2}+\frac{I}{C},
$$
$\frac{d \mathscr{E}}{d t}=0$인 경우, 위 방정식의 해는 다음과 같이 얻어진다.
$$
\begin{gathered}
I=\left(A e^{i \omega_n t}+B e^{-i \omega_n r}\right) e^{-R t / 2 L}, \\
\omega_n=\sqrt{\frac{1}{L C}-\frac{R^2}{4 L^2}},
\end{gathered}
$$
여기서 $A$와 $B$는 이제 결정해야할 상수들이다.
$\omega_n$는 자연 진동수(natural frequency)라고 한다.
$t=0$인 시점에서는 전류가 0이므로, 다음과 같은 형식으로 식이 세워져야 함을 알 수 있다.
$$
I(t)=D e^{-R t / 2 L} \sin \omega_n t
$$
여기서 $D$는 결정해야할 상수이다.
$t=0$일 때, 다음이 성립함을 고려하면, 위식의 계수 $D$가 결정된다.
$$
\mathscr{E}=\left.L \frac{d I}{d t}\right|_{t=0}
$$
$$
D=\frac{\mathscr{E}}{\omega_n L}=\frac{\mathscr{E}}{\sqrt{\frac{L}{C}-\frac{R^2}{4}}}
$$

• 미분방정식의 풀이
$$
R \frac{d I}{d t}+L \frac{d^2 I}{d t^2}+\frac{I}{C} = 0
$$
위 방정식을 좀더 정리하면
$$
\frac{d^2 I}{d t^2} + \frac{R}{L} \frac{d I}{d t} + \frac{I}{LC} = 0
$$
위 방식의 해가 $I=\alpha e^{\beta t}$의 형태로 주어진다고 가정하면,
일반해는 $I=\alpha_1 e^{\beta_1 t} + \alpha_2 e^{\beta_2 t}$로 주어진다.
계수들 $\alpha$와 $\beta$을 결정하자.
이 계수들을 결정하기 위해서 설정된 해를 방정식에 대입해 보자.
$$
\alpha \beta^2 e^{\beta t} + \frac{R}{L} \alpha \beta e^{\beta t} + \frac{\alpha e^{\beta t}}{LC} = 0
$$
정리하면,
$$
\beta^2 + \frac{R}{L} \beta + \frac{1}{LC} = 0
$$
위 $\beta$의 2차방정식의 해는 다음과 같이 주어진다.
$$
\beta = \frac{-\frac{R}{L} \pm \sqrt{\left(\frac{R}{L}\right)^2 - \frac{4}{LC}}}{2}
$$
여기서 $\left(\frac{R}{L}\right)^2 < \frac{4}{LC}$인 경우를 생각해보자. 이 경우 root안이 음수가 되기 때문에,
복소수형태로 기술하자.
정리하면,
$$
\beta = -\frac{R}{2L} \pm i\sqrt{\frac{1}{LC} - \left(\frac{R}{2L}\right)^2 }
$$
여기서 다음과 같이 정의하자.
$$\sqrt{\frac{1}{LC} - \left(\frac{R}{2L}\right)^2 } = \omega_n$$
정리하면,
$$
\begin{aligned}
\beta_1 &= -\frac{R}{2L} + i \omega_n \\
\beta_2 &= -\frac{R}{2L} - i \omega_n \\
\end{aligned}
$$
해는 다음과 같이 주어진다.
$$
\begin{aligned}
I &= \alpha_1 e^{ -\frac{R}{2L}t + i \omega_n t} + \alpha_2 e^{-\frac{R}{2L}t - i \omega_n t} \\
&= e^{ -\frac{R}{2L}t} \left(\alpha_1 e^{ i \omega_n t} + \alpha_2 e^{ - i \omega_n t} \right) \\
\end{aligned}
$$
11.3 교류 회로

$$
\mathscr{E}(t)=\mathscr{E}_0 \cos \omega t,
$$
위와 같은 교류기전력이 있을때
$$
\begin{aligned}
& \frac{d \mathscr{E}_1}{d t}+i \frac{d \mathscr{E}_2}{d t} \\
& =\left(L \frac{d^2 I_1}{d t^2}+R \frac{d I_1}{d t}+\frac{I_1}{C}\right) \\
& + i\left(L \frac{d^2 I_2}{d t^2}+R \frac{d I_2}{d t}+\frac{I_2}{C}\right)
\end{aligned}
$$
$$
i \omega \mathscr{E}_0 e^{i \omega t}=\left[-\omega^2 L+i \omega R+\frac{1}{C}\right] I_0 e^{i \omega t} .
$$
$$
\mathscr{E}_0 e^{i \omega t}=\left[R+i \omega L+\frac{1}{i \omega C}\right] I_0 e^{i \omega t},
$$
여기서 계수를 $Z$로 두면, 다음과 같이 된다.
$$
\mathscr{E}_0 e^{i \omega t}=Z I_0 e^{i \omega t}
$$
$$
\begin{aligned}
& Z=R+i \omega L+\frac{1}{i \omega C}, \\
& Z=R+i\left(\omega L-\frac{1}{\omega C}\right)
\end{aligned}
$$
$Z$는 회로의 임피던스(impedance)라고 한다.
임피던스의 실수부는 저항이고, 허수부는 리액턴스(reactance) $X$라고 한다.
리액턴스는 유도성 리액턴스(inductive reactance) $X_L=\omega L$과 축전성 리액턴스(capacitive reactance) $X_C=-1/(\omega C)$로 이루어져 있다.
임피던스는 다음과 같이 극 좌표 형태로 쓸수있다.
$$
\begin{gathered}
Z=|Z| e^{i \theta} \\
|Z|=\sqrt{R^2+(\omega L-1 / \omega C)^2} \\
\theta=\tan ^{-1}\left(\frac{\omega L-1 / \omega C}{R}\right)
\end{gathered}
$$
그러면 복소전류는 다음과 같고,
$$
I(t) = \frac{\mathscr{E}}{Z} = \frac{\mathscr{E}_0}{|Z|} e^{i(\omega t-\theta)}
$$
실제전류는 위 전류의 실수부 이므로 다음과 같이 주어진다.
$$
I(t)=\frac{\mathscr{E}_0}{|Z|} \cos (\omega t-\theta)
$$
• $\theta > 0$
$X_L > X_C$
회로가 유도적이다(more inductive than capacitive).
• $\theta < 0$
$X_L > X_C$
회로가 축전성이다(more capacitive than inductive).
• $\theta = 0$
$X_L = X_C$
회로가 공명(resonance)상태에 있다. $Z$의 최소 조건.

11.4 연결된 impedance들
• 직렬연결
$$
Z=Z_1+Z_2+Z_3+\cdots
$$
$$
Z_1=R
$$
$$
Z_2=i \omega L
$$
$$
Z_3=\frac{1}{i \omega C},
$$
$$
Z=Z_1+Z_2=\left(R_1+R_2\right)+i\left(X_1+X_2\right) \text {. }
$$
$$
\begin{gathered}
Z=|Z| e^{i \theta}, \quad|Z|=\left[\left(R_1+R_2\right)^2+\left(X_1+X_2\right)^2\right]^{1 / 2}, \\
\theta=\tan ^{-1} \frac{X_1+X_2}{R_1+R_2} .
\end{gathered}
$$
• 병렬연결
$$
\begin{aligned}
I & = I_1+I_2+\cdots \\
& = \frac{V}{Z_1}+\frac{V}{Z_2}+\cdots = V\left(\frac{1}{Z_1}+\frac{1}{Z_2}+\cdots\right)
\end{aligned}
$$
$$
\frac{1}{Z}=\frac{1}{Z_1}+\frac{1}{Z_2}+\cdots
$$
(예제)

위 그림과 같은 회로의 임피던스를 구하라.
$$
Z=R_1+\frac{1}{\frac{1}{R_2+i \omega L}+\frac{1}{1 / i \omega C}}
$$
$$
Z=R_1+\frac{\left(R_2+i \omega L\right)\left[\left(1-\omega^2 L C\right)-i \omega R_2 C\right]}{\left(1-\omega^2 L C\right)^2+\omega^2 R_2^2 C^2} .
$$
\begin{aligned}
Z&=R_1+\frac{R_2}{\left(1-\omega^2 L C\right)^2+\omega^2 R_2^2 C^2} \\
&+i \frac{\omega L\left(1-\omega^2 L C\right)-\omega R_2^2 C}{\left(1-\omega^2 L C\right)^2+\omega^2 R_2^2 C^2}
\end{aligned}
전류는 다음과 같이 주어진다.
\begin{aligned}
I = \frac{\mathscr{E}}{Z}
\end{aligned}
11.5 전력

순간전력은 가음과 같이 주어진다.
$$
P(t)=\operatorname{Re} I(t) \operatorname{Re} V(t)
$$
평균전력은 다음과 같다.
\begin{align}
\bar{P}&=\overline{\operatorname{Re} I(t) \operatorname{Re} V(t)}=\frac{1}{2}\left|I_0\right|\left|V_0\right| \cos \theta \\
&=\frac{1}{2} \frac{\left|V_0\right|^2}{|Z|^2} \operatorname{Re} Z
\end{align}
위 식에서 $\cos \theta$을 전력인자(power facror)라고 부른다.
전압과 전류의 유효값은 다음과 같이 정의한다.
$$
V_{\text {eff }}=\frac{\sqrt{2}}{2}\left|V_0\right|, \quad I_{\text {eff }}=\frac{\sqrt{2}}{2}\left|I_0\right| .
$$
11.6 공명(resonance)

회로의 Quality factor(품질 인자) $Q$.
$$Q=\frac{\omega_0}{2|\Delta \omega|} = \omega_0 L / R$$
유도과정
$$
\left|\omega L-\frac{1}{\omega C}\right|=R .
$$
\begin{equation}
\begin{aligned}
& \left|\omega_0 L+\Delta \omega L-\frac{1}{\omega_0 C} \frac{1}{1+\Delta \omega / \omega_0}\right|=R \\
& \text { and }\left(1+\Delta \omega / \omega_0\right)^{-1} \cong 1-\Delta \omega / \omega_0 \text { gives } \\
& 2|\Delta \omega| L=R \\
& \frac{2|\Delta \omega|}{\omega_0}=\frac{R}{\omega_0 L} . \\
& Q=\omega_0 L / R \quad \text { or } \quad Q=\frac{\omega_\sigma}{2|\Delta \omega|}
\end{aligned}
\end{equation}

$$
Z=\omega_0 L\left[\frac{\omega_0 L}{R}-i\right], \quad\left(\omega=\omega_0\right)
$$
11.7 교류회로에서 상호인덕턴스
(에제1)

$$
\mathscr{E}_2=M_{21} \frac{d I_1}{d t} .
$$
$$
\mathscr{E}_2=i \omega M_{21} I_{10} e^{i \omega t}
$$
$$
\mathscr{E}_2=i \omega M_{21} I_1
$$
$$
Z_1 I_1+i \omega L_1 I_1+i \omega M_{12} I_2=\mathscr{E}
$$
$$
i \omega M_{12} I_1+Z_2 I_2+i \omega L_2 I_2=\mathscr{E},
$$
$$
\begin{aligned}
& I_1=\mathscr{E} \frac{Z_2+i \omega L_2-i \omega M_{12}}{\left(Z_1+i \omega L_1\right)\left(Z_2+i \omega L_2\right)+\omega^2 M_{12}^2} \\
& I_2=\mathscr{E} \frac{Z_1+i \omega L_1-i \omega M_{12}}{\left(Z_1+i \omega L_1\right)\left(Z_2+i \omega L_2\right)+\omega^2 M_{12}^2}
\end{aligned}
$$
$$
I=I_1+I_2=\mathscr{E} \frac{Z_1+i \omega L_1+Z_2+i \omega L_2-2 i \omega M_{12}}{\left(Z_1+i \omega L_1\right)\left(Z_2+i \omega L_2\right)+\omega^2 M_{12}^2} .
$$
(에제2)

$$
\left.\begin{array}{r}
\left(Z_1+i \omega L_1\right) I_1-i \omega M_{12} I_2=\mathscr{E} \\
-i \omega M_{12} I_1+\left(Z_2+i \omega L_2\right) I_2=\mathscr{E} .
\end{array}\right\}
$$
$$
Z_{a b}=\frac{\left(Z_1+i \omega L_1\right)\left(Z_2+i \omega L_2\right)+\omega^2 M_{12}^2}{Z_1+i \omega L_1+Z_2+i \omega L_2+2 i \omega M_{12}}
$$
(에제3)

$$
\begin{aligned}
\mathscr{E}&=I_1 R_1+i \omega L_1 I_1+i \omega M I_2 \\
0 &=I_2 R_2+i \omega L_2 I_2+i \omega M I_1+I_2 Z_L
\end{aligned}
$$
$$
\begin{aligned}
I_1&=\frac{Z_L+R_2+i \omega L_2}{\left(R_1+i \omega L_1\right)\left(Z_L+R_2+i \omega L_2\right)+\omega^2 M^2} \mathscr{E} \\
I_2&=\frac{-i \omega M}{\left(R_1+i \omega L_1\right)\left(Z_L+R_2+i \omega L_2\right)+\omega^2 M^2} \mathscr{E}
\end{aligned}
$$
위 식을 다음과 같이 줄여서 써보자.
$$
\begin{aligned}
I_1&= \frac{\mathscr{E}}{Z_1} \\
I_2&= \frac{\mathscr{E}}{Z_2}
\end{aligned}
$$
여기서 $Z_1$과 $Z_2$는 다음과 같이 주어진다.
$$\frac{1}{Z_1} = \frac{Z_L+R_2+i \omega L_2}{\left(R_1+i \omega L_1\right)\left(Z_L+R_2+i \omega L_2\right)+\omega^2 M^2}$$
$$\frac{1}{Z_2} = \frac{-i \omega M}{\left(R_1+i \omega L_1\right)\left(Z_L+R_2+i \omega L_2\right)+\omega^2 M^2}$$
$\mathscr{E}$이 다음과 같이 주어진다고 하자.
$$\mathscr{E} = \mathscr{E}_0 e^{-i\omega t} $$
$Z_1$과 $Z_2$는 복소수이므로 다음과 같이 표현할 수 있다.
$$
\begin{aligned}
Z_1& = \left| Z_1 \right| e^{i\theta_1}\\
Z_2& = \left| Z_2 \right| e^{i\theta_2}
\end{aligned}
$$
여기서 위 복소수의 크기와 각도는 다음과 같이 실수부($Z_r$)와 허수부($Z_i$)로 구하거나
$$\left| Z \right| = \sqrt{Z_r^2+Z_i^2}$$
$$\theta = \mathrm{arctan}(Z_i/Z_r)$$
파이썬의 numpy 모듈로 구할 수 있다.
$$\left| Z \right| \rightarrow \mathrm{np.abs}$$
$$\theta \rightarrow \mathrm{np.angle}$$
파이썬으로 복소수 계산시 복소수 $i$는 $1j$로 표기하여 계산하면 된다.
11.8 Mesh와 nodal 방정식들

$$
\begin{array}{cccc}
I_1\left(Z_3+Z_4\right) & -I_2 Z_4 & -I_3 Z_3 & =\mathscr{v}, \\
-I_1 Z_4 & +I_2\left(Z_1+Z_2+Z_4\right) & -I_3 Z_2 & =0, \\
-I_1 Z_3 & -I_2 Z_2 & +I_3\left(Z_2+Z_3+Z_5\right) & =0 .
\end{array}
$$
$$
\sum_{j=1}^n Z_{i j} I_j=\mathscr{E}_i(i=1,2, \ldots, n)
$$

\begin{equation}
\begin{aligned}
I_1\left(Z_1+Z_2\right)+I_2 Z_2 & =\mathscr{E}_1 \\
I_1 Z_2+I_2\left(Z_2+Z_3\right) & =\mathscr{E}_2
\end{aligned}
\end{equation}
$$
\mathscr{I}(t)=\frac{V_1}{Z_1}+\frac{V_1-V_2}{Z_2}
$$
$$
0=\frac{V_2-V_1}{Z_2}+\frac{V_2}{Z_3}+\frac{V_2}{Z_4} .
$$
임피던스의 역수를 얻미턴스(admittance)라고 하고 $Y$로 표기한다.
$$
\begin{aligned}
\mathscr{I}(t) & =\left(Y_1+Y_2\right) V_1-Y_2 V_2, \\
0 & =-Y_2 V_1+\left(Y_2+Y_3+Y_4\right) V_2,
\end{aligned}
$$

$$
\begin{aligned}
\mathscr{I}_1 & =Y_1 V_1+Y_2\left(V_1-V_2\right)+Y_4\left(V_1-V_3\right) \\
0 & =Y_2\left(V_2-V_1\right)+Y_3 V_2+Y_5\left(V_2-V_3\right) \\
\mathscr{I}_2 & =Y_6 V_3+Y_5\left(V_3-V_2\right)+Y_4\left(V_3-V_1\right)
\end{aligned}
$$