12. Maxwell 방정식

12.1 Ampere–Maxwell 법칙

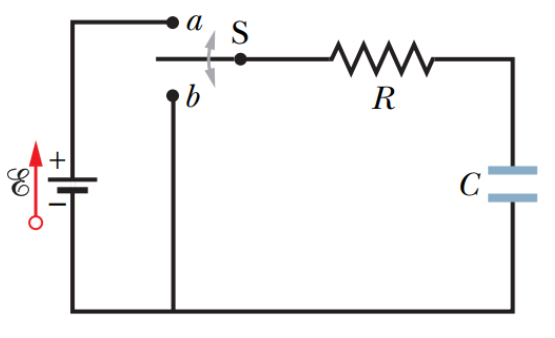
그림1
위 그림에서 보는 바와 같이 R-C 회로에서 스위치를 닫는 직후에 축전기에 순간적으로 전하가 과도하게 축적이 되었다가 흩어지면서 발생하는 일시적 전류가 존재한다는 것을 우리는 배웠다.

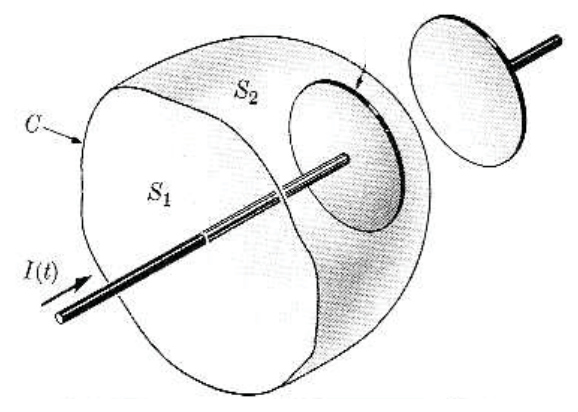
그림2
만약 위 그림과 같이 축전기로 들어가는 도선 근처의 폐경로 $C$에 대해 Ampere 법칙을 적용해보자. Ampere 법칙을 적용시 우변의 전류 $I$는 Ampere 경로를 관통하는 전류라고 우리는 알고있다. 여기서 전류 $I$가 관통한다는 것은 좀더 세부적으로는 어떤 면을 관통한다는 것을 주의할필요가 있다. 지금까지는 그 면을 편의상 그 경로를 가장자리로하는 평면이라고 주로 설정하였지만, 수학적으로 보면 그 경로를 가장자리로하는 어떠한 면도 선택될 수 있다. 그래서 그림2에서 보이는 바와 같이 경로 $C$를 가장자리로 하는 면 $S_1$와 $S_2$에 대해서 Ampere 법칙을 적용하면 다음 두 식들을 얻게 된다. $$ \oint_C \vec{H} \cdot d \vec{\ell}=\int_{S_1} \vec{J} \cdot d\vec{A}=I $$ $$ \oint_C \vec{H} \cdot d \vec{\ell}=\int_{S_2} \vec{J} \cdot d\vec{A}=0 $$ 위 식들에서 보는 바와 같이 동일한 경로 $C$에 대해서 Ampere 법칙을 적용하였지만 우변에 다른 결과가 나오는 것을 알 수 있다. 스위치를 닫은 직후 전하가 축전기에 쌓이고 있는 상황에서 $S_1$을 통과하는 전류는 있지만, $S_2$를 통과하는 전류는 존재하지 않기 때문이다. 이것은 단순한 Ampere 법칙만으로는 이러한 일시적 현상을 기술할 수 없다는 것을 알수있다. 이 문제를 해결하기 위해서 다음과 같이 주어지는 Ampere 법칙의 미분형으로 접근해 보자. $$ \nabla \times \vec{H}=\vec{J} $$ 위 식의 양변에 divergence를 취하면, 좌변은 0이지만, 우변은 다음의 연속방정식에 의해 0일 수 도 있고 아닐 수도 있는 상황이 발생한다. $$ \nabla \cdot \vec{J}+\frac{\partial \rho}{\partial t}=0 $$ 그러나 좌변이 0기 때문에 수학적으로는 우변 또한 0이어야만 한다. 연속방정식을 만족하면서도, Ampere법칙이 모순되지 않게 하는 방법은 연속방정식에서 나오는 $\rho$를 다음의 Gauss법칙의 미분형을 이용하여 $\vec{D}$로 표현해보는 것이다. $$ \nabla \cdot \vec{D}=\rho $$ 그러면 다음이 성립한다. $$ \nabla \cdot\left(\vec{J}+\frac{\partial \vec{D}}{\partial t}\right)=0 $$ 위 식은 $\frac{\partial \vec{D}}{\partial t}$이 전류의 차원을 가진다는 것을 의미하면서, $\vec{J}+\frac{\partial \vec{D}}{\partial t}$에 divergence를 취하면 0이라는 것을 얻을 수 있다는 것을 의미한다. 그래서 Ampere법칙 미분형의 양변에 divergence를 취했을 때, 좌변은 0이고, 우변이 0이 되기 위해서는 Ampere법칙 미분형의 우변에 $\frac{\partial \vec{D}}{\partial t}$을 추가해야한다는 것을 알 수 있다. 이렇게 수정된 Ampere법칙을 Ampere–Maxwell 법칙이라고한다. $$\nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t}$$ 지금까지 얻어진 전기및 자기 방정식들을 정리하면 다음과 같고, 아래 방정식들을 Maxwell 방정식이라고 한다. \begin{equation} \begin{aligned} & \nabla \cdot \vec{D}=\rho \\ & \nabla \cdot \vec{B}=0 \\ & \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \\ & \nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t} \end{aligned} \end{equation} 아래 식들은 Maxwell 방정식의 적분형이라고 한다. \begin{equation} \begin{aligned} & \oint \vec{E} \cdot d \vec{A}= \frac{Q}{\varepsilon_0} \\ & \oint \vec{B} \cdot d \vec{A}=0 \\ & \oint \vec{E} \cdot d \vec{s}=-\frac{d \Phi_B}{d t} \\ & \oint \vec{B} \cdot d \vec{s}= \mu_0 I + \mu_0 \epsilon_0 \frac{d \Phi_E}{d t} \end{aligned} \end{equation} 전자기학의 모든 문제는 Maxwell 방정식으로 다 기술된다고 할 수 있다.
Ampere–Maxwell 법칙이 의미하는 것은 실제전류가 아닌 전기다발 $\Phi_E$의 시간변화율($\frac{d \Phi_E}{d t}$)도 자기장을 유도해낸다는 것을 의미한다. 이것은 $\frac{d \Phi_E}{d t}$이 자가장을 생성하는 마치 전류와 같은 역할을 한다고도 볼수있다. 그래서 $\epsilon_0\frac{d \Phi_E}{d t}$을 변위 전류(displacement current) $I_d$라고 부른다. Ampere–Maxwell 법칙은 다음과 같이 기술될 수 있다. $$\oint \vec{B} \cdot d \vec{s}= \mu_0 (I + I_d)$$
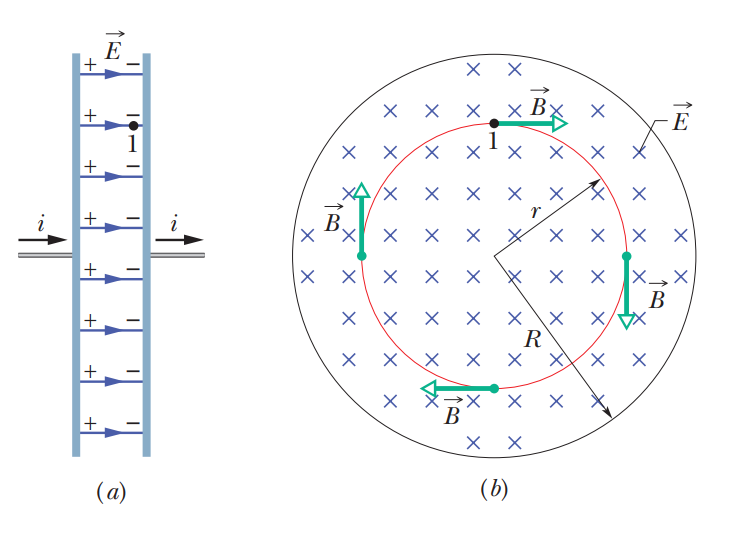
$\frac{d \Phi_E}{d t}$의 부호에 따른 생성된 자기장의 방향은 그림에서 잘 설명되고 있다. $\Phi_E$가 시간에 따라 증가하면, 오른손 형상에 따라서 결정되는 방향으로 자기장이 발생하는 것을 보여준다.
(예제) 풀이

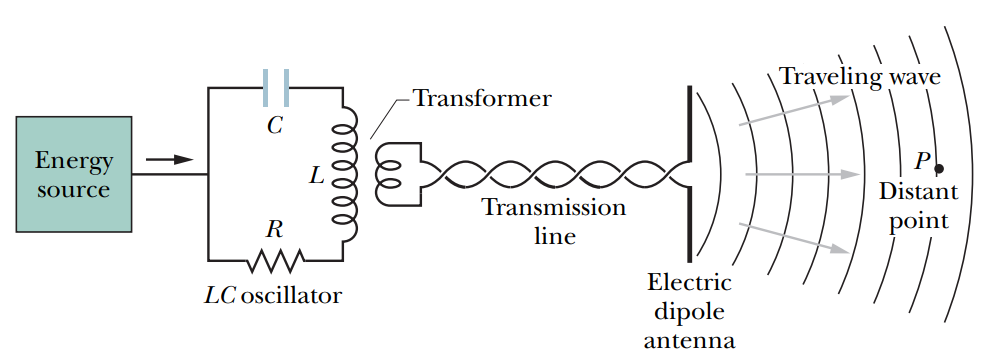
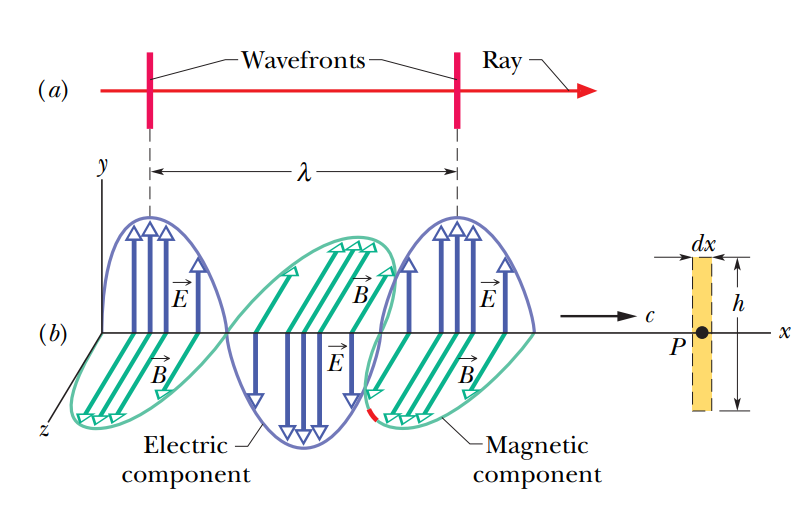
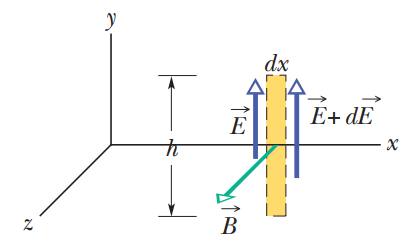
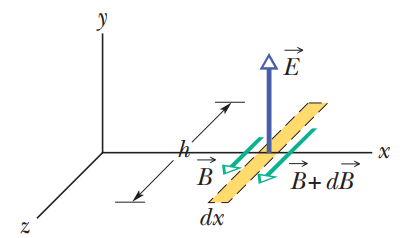
12.2 전자기파

전기다발의 시간변화가 자기장을 생성한다는 것에 대한 대표적인 증거는 바로 전자기파의 존재이다. Maxwell 방정식의 마지막 식의 양변에 curl을 취하면 다음식을 얻는다. $$ \nabla \times \nabla \times \vec{H}=\nabla \times \vec{J}+\nabla \times \frac{\partial \vec{D}}{\partial t} $$ $$ \nabla \times \nabla \times \vec{H}=g \nabla \times \vec{E}+\epsilon \frac{\partial}{\partial t} \nabla \times \vec{E} $$ $$ \nabla \times \nabla \times \vec{H}=-g \mu \frac{\partial \vec{H}}{\partial t}-\epsilon \mu \frac{\partial^2 \vec{H}}{\partial t^2} $$ $$ \nabla \times \nabla \times=\nabla \nabla \cdot-\nabla^2 $$ $$ \nabla \nabla \cdot \vec{H}-\nabla^2 \vec{H}=-g \mu \frac{\partial \vec{H}}{\partial t}-\epsilon \mu \frac{\partial^2 \vec{H}}{\partial t^2} $$ 다음 식을 적용하면, $$ \nabla \cdot \vec{H}=\frac{1}{\mu} \nabla \cdot \vec{B}=0 $$ 결과적으로 다음과 같은 $\vec{H}$에 대한 파동방정식을 얻게 된다. $$ \nabla^2 \vec{H}-\epsilon \mu \frac{\partial^2 \vec{H}}{\partial t^2}-g \mu \frac{\partial \vec{H}}{\partial t}=0 $$ Maxwell 방정식에서 Faraday 유도법칙의 양변에 curl을 취하면 다음 식을 얻는다. $$ \nabla \times \nabla \times \vec{E}=-\nabla \times \frac{\partial \vec{B}}{\partial t} $$ $$ \nabla \times \nabla \times \vec{E}=-g \mu \frac{\partial \vec{E}}{\partial t}-\epsilon \mu \frac{\partial^2 \vec{E}}{\partial t^2} $$ 결과적으로 $\vec{E}$에 대한 파동방정식을 얻게 된다. $$ \nabla^2 \vec{E}-\epsilon \mu \frac{\partial^2 \vec{E}}{\partial t^2}-g \mu \frac{\partial \vec{E}}{\partial t}=0 $$ 파동방정식
\begin{equation} \frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2} \frac{\partial^2 y}{\partial t^2} \end{equation} 파동방정식의 해
\begin{equation} y(x, t)=y_m \sin (k x-\omega t) \end{equation} \begin{equation} \frac{d x}{d t}=v=\frac{\omega}{k} \end{equation}

12.3 전자기 에너지

이미 배운바와 같이 전기에너지와 자기에너지는 다음과 같이 주어진다. $$ U_E=\frac{1}{2} \int_V \vec{E} \cdot \vec{D} d v $$ $$ U_M=\frac{1}{2} \int_V \vec{H} \cdot \vec{B} d v $$ 전자기파는 전기장과 자기장으로 이루어진것으로 파동의 형태로 이동한다는 것은 곧 에너지도 이동이 된다는 것을 의미한다. 전자기파에 의한 에너지 이동에 대해서 알아보자. Maxwell 방정식에 $\vec{H} \cdot$와 $\vec{E} \cdot$을 취하고 적절히 조합하면 다음이 얻어진다. $$ \vec{H} \cdot \nabla \times \vec{E}-\vec{E} \cdot \nabla \times \vec{H}=-\vec{H} \cdot \frac{\partial \vec{B}}{\partial t}-\vec{E} \cdot \frac{\partial \vec{D}}{\partial t}-\vec{E} \cdot \vec{J} $$ 다음 항등식을 위 식의 좌변에 적용하면, $$ \nabla \cdot(\vec{F} \times \vec{G})=\vec{G} \cdot \nabla \times \vec{F}-\vec{F} \cdot \nabla \times \vec{G} $$ 다음 식이 얻어진다. $$ \nabla \cdot(\vec{E} \times \vec{H})=-\vec{H} \cdot \frac{\partial \vec{B}}{\partial t}-\vec{E} \cdot \frac{\partial \vec{D}}{\partial t}-\vec{E} \cdot \vec{J} $$ 다음 관계식들을 적용하면, $$ \vec{E} \cdot \frac{\partial \vec{D}}{\partial t}=\vec{E} \cdot \frac{\partial}{\partial t} \epsilon \vec{E}=\frac{1}{2} \epsilon \frac{\partial}{\partial t} \vec{E}^2=\frac{\partial}{\partial t} \frac{1}{2} \vec{E} \cdot \vec{D} $$ $$ \vec{H} \cdot \frac{\partial \vec{B}}{\partial t}=\vec{H} \cdot \frac{\partial}{\partial t} \mu \vec{H}=\frac{1}{2} \mu \frac{\partial}{\partial t} \vec{H}^2=\frac{\partial}{\partial t} \frac{1}{2} \vec{H} \cdot \vec{B} $$ 다음 식이 얻어진다. $$ \nabla \cdot(\vec{E} \times \vec{H})=-\frac{\partial}{\partial t} \frac{1}{2}(\vec{E} \cdot \vec{D}+\vec{B} \cdot \vec{H})-\vec{J} \cdot \vec{E} $$ 위 식을 공간 $V$에 대해서 적분하면 다음 식이 얻어진다. $$ \int_V \nabla \cdot(\vec{E} \times \vec{H}) d v=-\frac{d}{d t} \int_V \frac{1}{2}(\vec{E} \cdot \vec{D}+\vec{B} \cdot \vec{H}) d v-\int_V \vec{J} \cdot \vec{E} d v $$ $$ \oint_S \vec{E} \times \vec{H} \cdot d\vec{A}=-\frac{d}{d t} \int_V \frac{1}{2}(\vec{E} \cdot \vec{D}+\vec{B} \cdot \vec{H}) d v-\int_V \vec{J} \cdot \vec{E} d v $$ $$ -\int_V \vec{J} \cdot \vec{E} d v=\frac{d}{d t} \int_V \frac{1}{2}(\vec{E} \cdot \vec{D}+\vec{B} \cdot \vec{H}) d v+\oint_S \vec{E} \times \vec{H} \cdot d\vec{A} $$ 여기서 다음과 같이 주어지는 Poynting vector($\vec{S}$)와 전자기에너지 밀도($u$)를 정의하면, $$ \begin{aligned} & \vec{S}=\vec{E} \times \vec{H} \\ & u=\frac{1}{2}(\vec{E} \cdot \vec{D}+\vec{B} \cdot \vec{H}) \end{aligned} $$ 다음과 같이 정리된다. $$ \nabla \cdot \vec{S}+\frac{\partial u}{\partial t}=-\vec{J} \cdot \vec{E} $$ $\vec{J}=0$인 경우에는 다음과 같이 주어진다. $$ \nabla \cdot \vec{S}+\frac{\partial u}{\partial t}=0 $$ 위 방정식은 연속방정식과 동일한 형태를 가지고 있다. Poynting vector($\vec{S}$)는 전자기파가 진행하는 방향 또는 에너지가 전달되는 방향을 표시한다.

12.4 근원이 없는 파동방정식의 해(단색파)

파동방정식에 대한 해가 다음과 같이 주어진다고 가정하고, \begin{equation} \vec{E}(\vec{r}, t)=\vec{E}(\vec{r}) e^{-i \omega t} \end{equation} 파동방정식에 대입하면 다음을 얻는다. $$ e^{-i \omega t}\left\{\nabla^2 \vec{E}+\omega^2 \epsilon \mu \vec{E}+i \omega g \mu \vec{E}\right\}=0 $$ 단순한 경우부터 알아보기 위해서 진공에서의 전파를 가정하면($g=0$), 다음을 얻는다. $$ \frac{d^2 \vec{E}(z)}{d z^2}+(\omega / c)^2 \vec{E}=0 $$ 여기서 $c$는 전자기파의 속력이며, 다음과 같이 주어진다. $$ \epsilon_0 \mu_0=1 / c^2 $$ 위 방정식은 단순조화진동자 방정식과 동일하므로 $\vec{E}(z)$을 다음과 같이 기술한다. $$ \vec{E}(z)=\vec{E}_0 e^{ \pm i \kappa z} $$ $$ \kappa=\omega / c $$ 전기장은 다음과 같이 기술된다. $$ \vec{E}(\vec{r}, t)=\vec{E}_0 e^{-i(\omega t \mp \boldsymbol{\kappa} z)} $$ $$ \vec{E}(\vec{r}, t)=\vec{E}_0 \cos (\omega t \mp \kappa z) $$ $$ \vec{E}(\vec{r}, t)=\vec{E}_0 \cos \omega(t \mp z / c) $$ 굴절율 $n$은 다음과 같이 정의된다. $$ n = \sqrt{K} = \sqrt{\epsilon/\epsilon_0}$$ $g \gg \omega \epsilon$인 경우, 다음이 성립한다. $$ \frac{d^2 \vec{E}(z)}{d^2 z}+i \omega g \mu \vec{E}=0 $$ $$ \kappa=\sqrt{\alpha g \mu} $$ $$ \vec{E}(\vec{r}, t)=\vec{E}(\vec{r}) e^{-\alpha t} $$ $$ \begin{array}{lcc} \text { Tipo de radiación EM } & \multicolumn{1}{c}{\begin{array}{c} \text { Frecuencia } \\ (\mathrm{Hz}) \end{array}} & \begin{array}{c} \text { Longitud de onda } \lambda \\ (\mathrm{m}) \end{array} \\ \hline \hline \text { Ondas de radio } & 10^4 \mathrm{a} 10^8 & 3 \mathrm{a} 3 \times 10^4 \\ \text { TV, FM } & 10^8 & 3 \\ \text { Microondas, RADAR } & 10^9 \mathrm{a} 10^{11} & 3 \times 10^{-3} \mathrm{a} 3 \times 10^{-1} \\ \text { Infrarrojo lejano } & 10^{12} & 3 \times 10^{-4} \\ \text { Radiación infrarroja } & 10^{13} \mathrm{a} 4 \times 10^{14} & 8 \times 10^{-7} \mathrm{a} 3 \times 10^{-5} \\ \text { Luz visible } & 4 \times 10^{14} \mathrm{a} 8 \times 10^{14} & 4 \times 10^{-7} \mathrm{a} 8 \times 10^{-7} \\ \text { Radiación ultravioleta } & 8 \times 10^{14} \mathrm{a} 10^{17} & 3 \times 10^{-9} \mathrm{a} 4 \times 10^{-7} \\ \text { Rayos X blandos } & 10^{17} \mathrm{a} 10^{19} & 3 \times 10^{-11} \mathrm{a} 3 \times 10^{-9} \\ \text { Rayos X } & 10^{19} \mathrm{a} 10^{20} & 3 \times 10^{-12} \mathrm{a} 3 \times 10^{-11} \\ \text { Rayos gamma } & 10^{19} \mathrm{a} 10^{22} & 3 \times 10^{-14} \mathrm{a} 3 \times 10^{-12} \end{array} $$

12.5 경계조건

12.6 근원이 있는 파동방정식의 해(단색파)