2. 양자역학 소개
2.0 배울 내용
• 반도체 소자물리를 이애하기 위한 양자역학의 기본적인 원리 논의
• Schrödinger's 파동방정식과 파동함수의 물리적 의미 논의
• 결정내의 전자들의 거동 특성을 이해하기 위해 Schrödinger's 파동방정식을 다양한 포텐셜 함수에 적용
• Schrödinger's 파동방정식을 1전자 원자에 적용. 이것의 결과는 4개의 기본양자수, 에너지 불연속화, 주기율표 초기 구축에 기여를 한다.
2.1 양자역학의 원칙들
2.1.1 에너지 양자(Energy Quanta)
• 흑체복사(blackbody radiation)
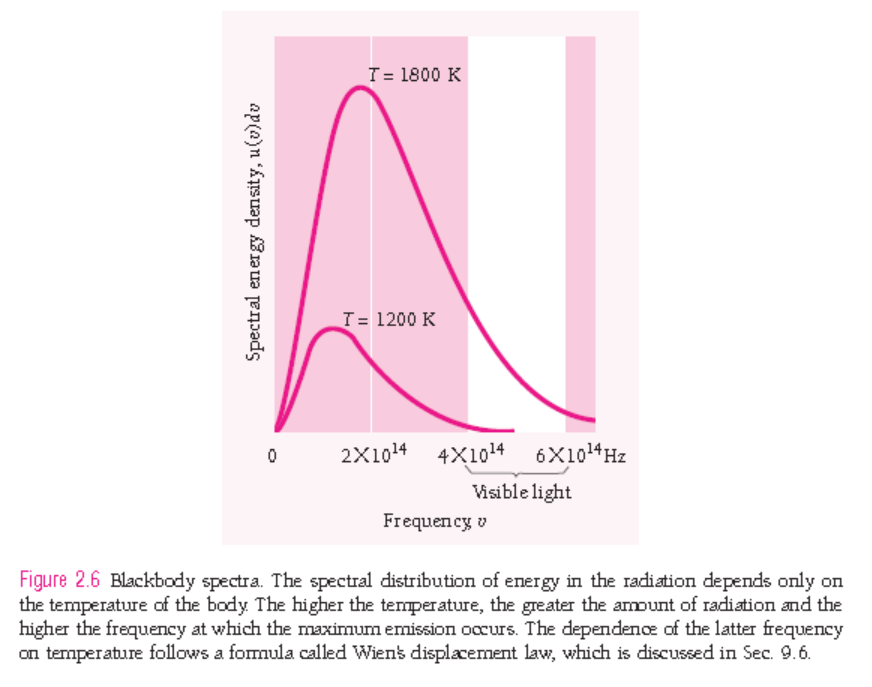
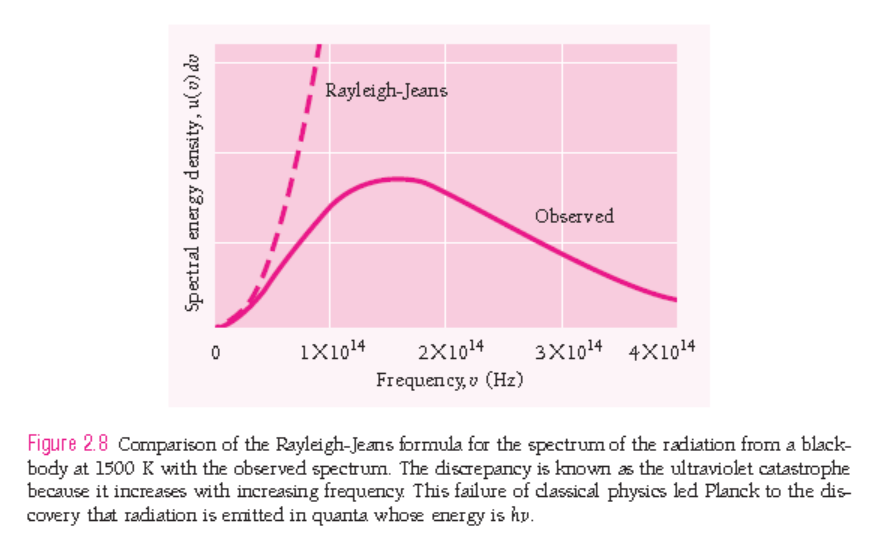
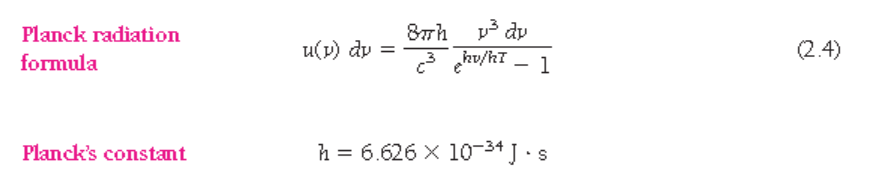
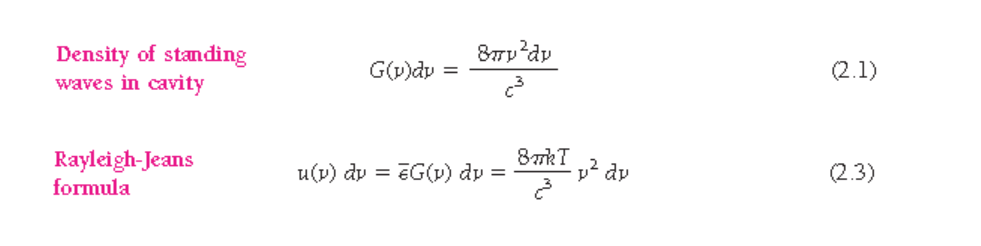$$ P = \frac{e^{-nh\nu/kT}}{\sum_{n=0}^{\infty}e^{-nh\nu/kT}} $$
$$ \left< E(\nu,T) \right> = \frac{\sum_{n=0}^{\infty} nh\nu e^{-nh\nu/kT} }{\sum_{n=0}^{\infty}e^{-nh\nu/kT}} $$
$$ = \frac{h\nu}{e^{h\nu/kT}-1} $$
에너지의 양자화. $E=h\nu$ :quanta, $h=6.625\times 10^{-34}$ Js.
2.1.2 파동의 입자성
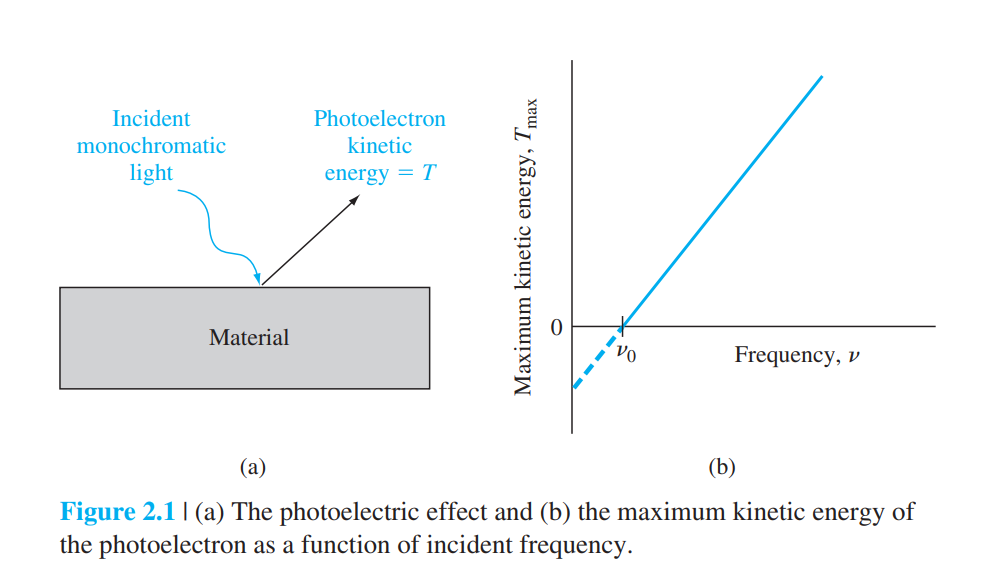
• 광전효과(photoelectric effect)
photon : 빛 에너지의 입자같은 wave packet
Work function(일함수): 전자를 제거하는데 필요한 최소에너지
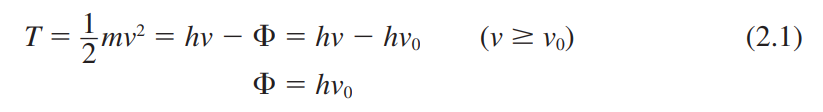
• Compton 효과
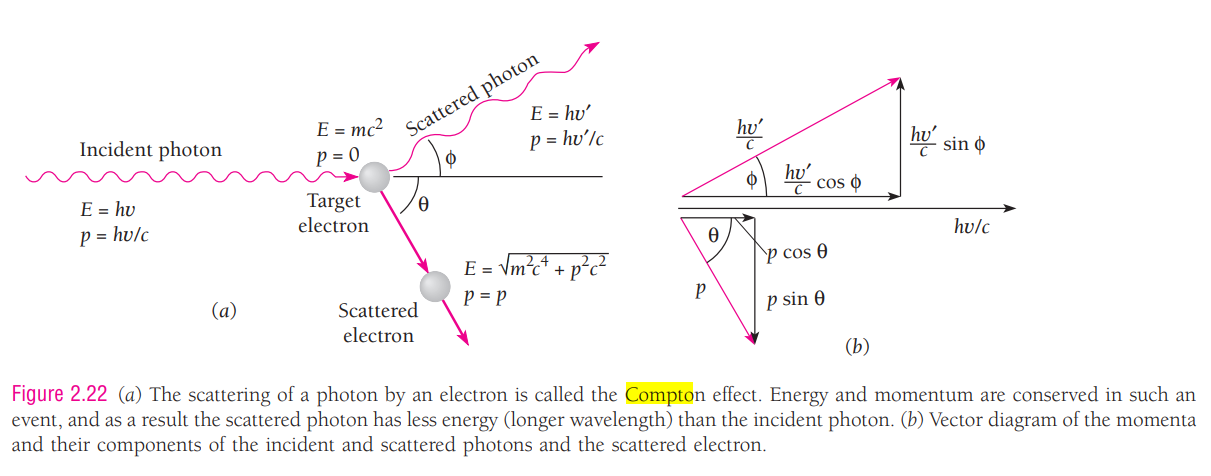$$ \vec{p}_{1,전} + \vec{p}_{2,전} = \vec{p}_{1,후} + \vec{p}_{2,후} $$
충돌 후 나오는 파의 파장이 길어짐을 발견
2.1.3 입자의 파동성
• Davisson과 Germer의 실험
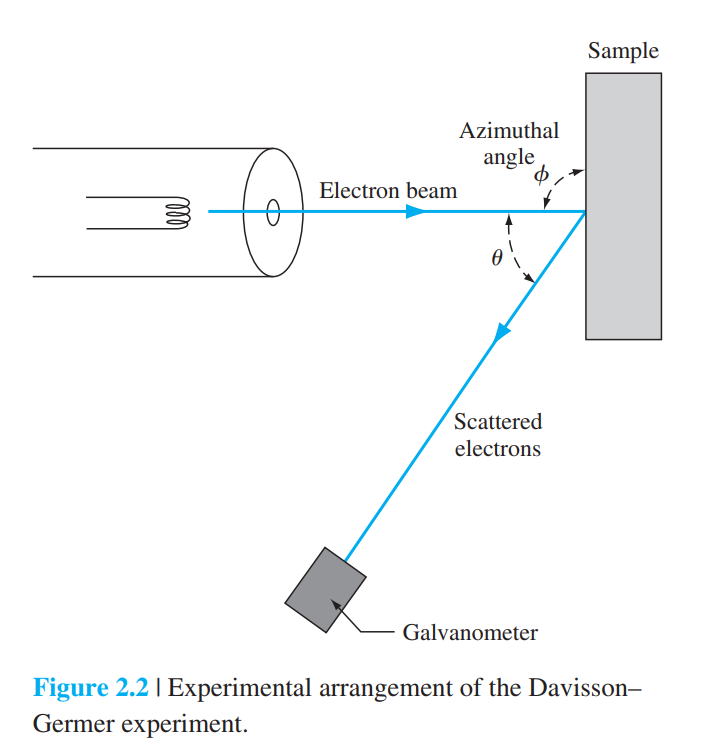
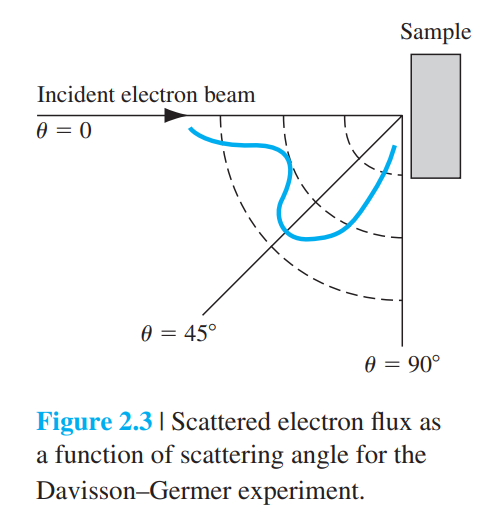
• 이중슬릿을 통과하는 전자
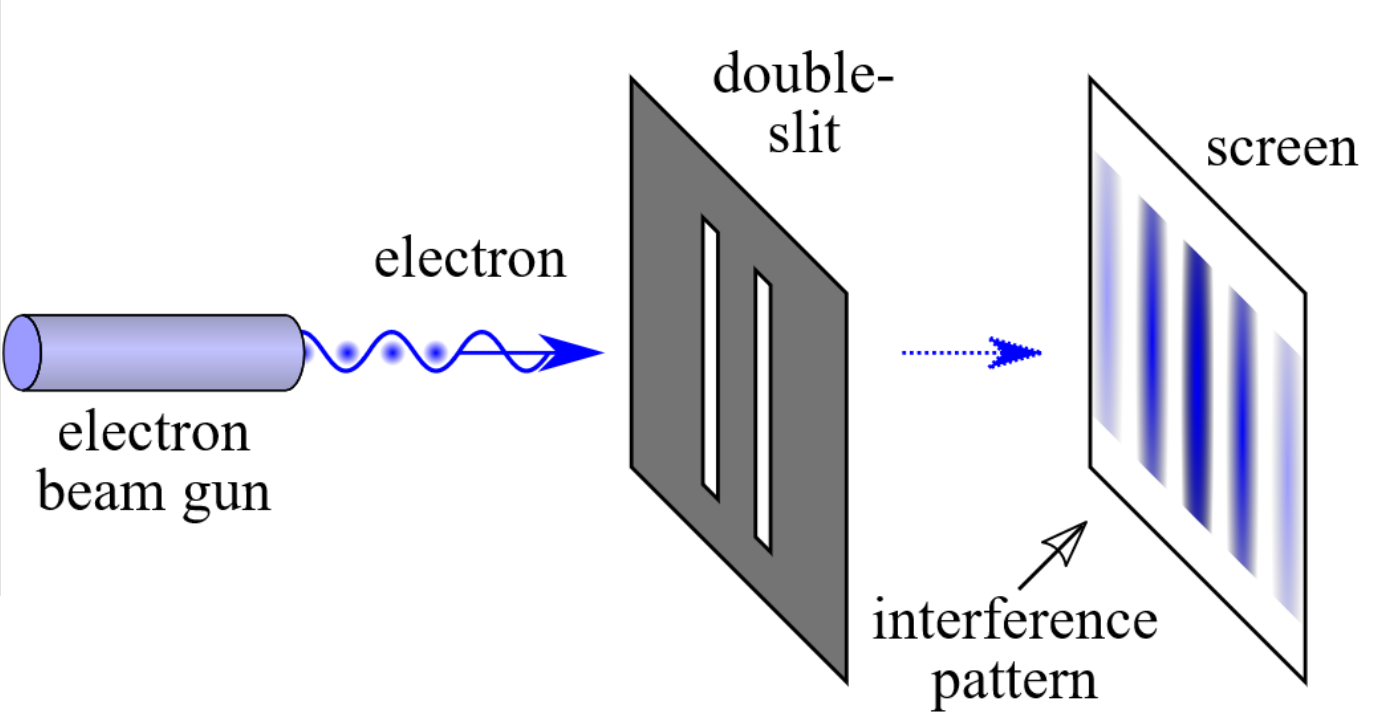
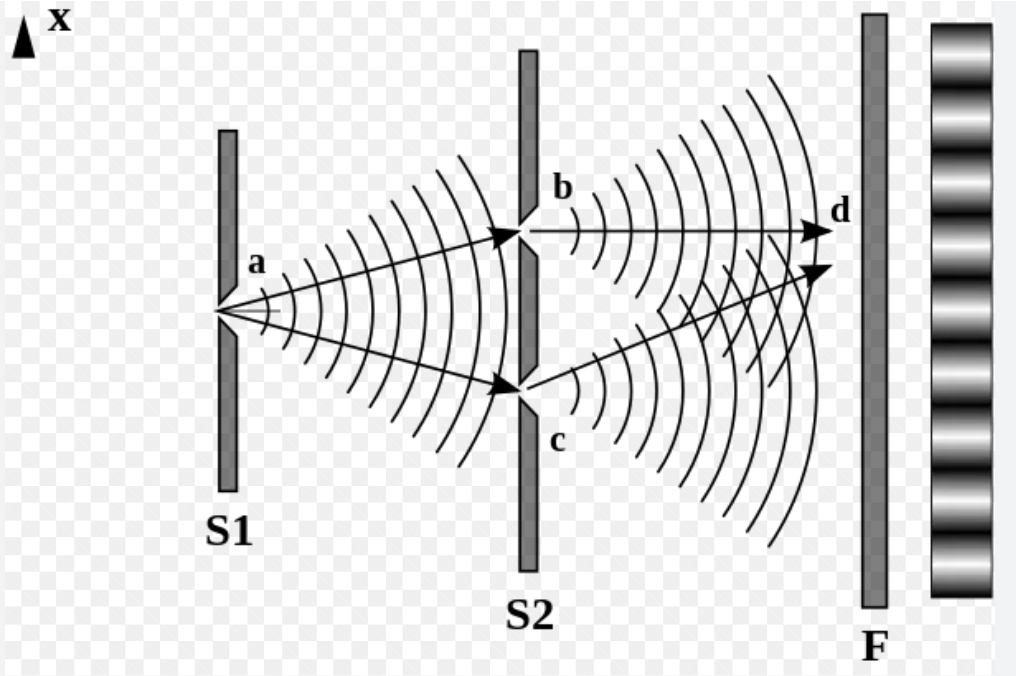
2.1.4 파동-입자 이중성(Wave–Particle Duality)
• de Broglie 가설
wave-particle 이중성 원리(duality principle)
$$p=\frac{h}{\lambda} \qquad (2.2)$$
$p$: photon의 운동량, $\lambda$ : 빛의 파장
$$\lambda=\frac{h}{p} \qquad (2.3)$$
$p$: 입자의 운동량, $\lambda$ : 물질파의 de Broglie 파장
2.1.5 불확정성의 원리(The Uncertainty Principle)
$$\Delta p \Delta x \geq \hbar $$
$$\Delta E \Delta t \geq \hbar $$
$\hbar = h/(2\pi) = 1.054\times 10^{34}$ Js
양자역학에서는 입자의 위치를 정확하게 말하는 대신 입자가 그 위치에 있을 확률을 결정한다.
• Fourier Series
어떠한 주기함수든 sin과 cos의 합으로 기술이 가능하다.
$$
F(t)=\frac{1}{2} a_0+\sum_{n=1}^{\infty}\left(a_n \cos n \omega t+b_n \sin n \omega t\right)
$$
계수는 다음과 같이 결정 된다.
$$
\left.\begin{array}{l}
a_n=\frac{2}{\tau} \int_0^\tau F\left(t^{\prime}\right) \cos n \omega t^{\prime} d t^{\prime} \\
b_n=\frac{2}{\tau} \int_0^\tau F\left(t^{\prime}\right) \sin n \omega t^{\prime} d t^{\prime}
\end{array}\right\}
$$
또는
$$
\left.\begin{array}{c}
a_n=\frac{\omega}{\pi} \int_{-\pi / \omega}^{+\pi / \omega} F\left(t^{\prime}\right) \cos n \omega t^{\prime} d t^{\prime} \\
b_n=\frac{\omega}{\pi} \int_{-\pi / \omega}^{+\pi / \omega} F\left(t^{\prime}\right) \sin n \omega t^{\prime} d t^{\prime}
\end{array}\right\}
$$
$$ F(t)=\frac{A}{\pi}\left[\sin \omega t-\frac{1}{2} \sin 2 \omega t+\frac{1}{3} \sin 3 \omega t-\cdots\right] $$
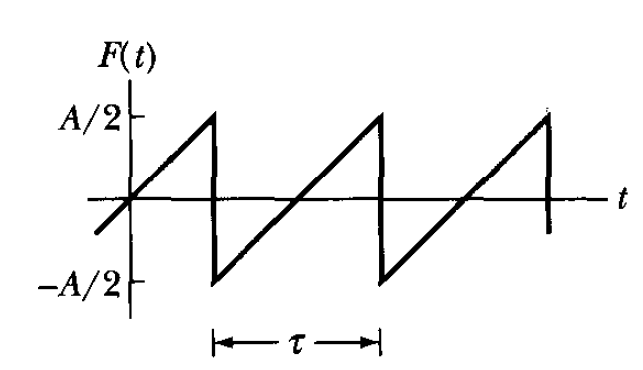
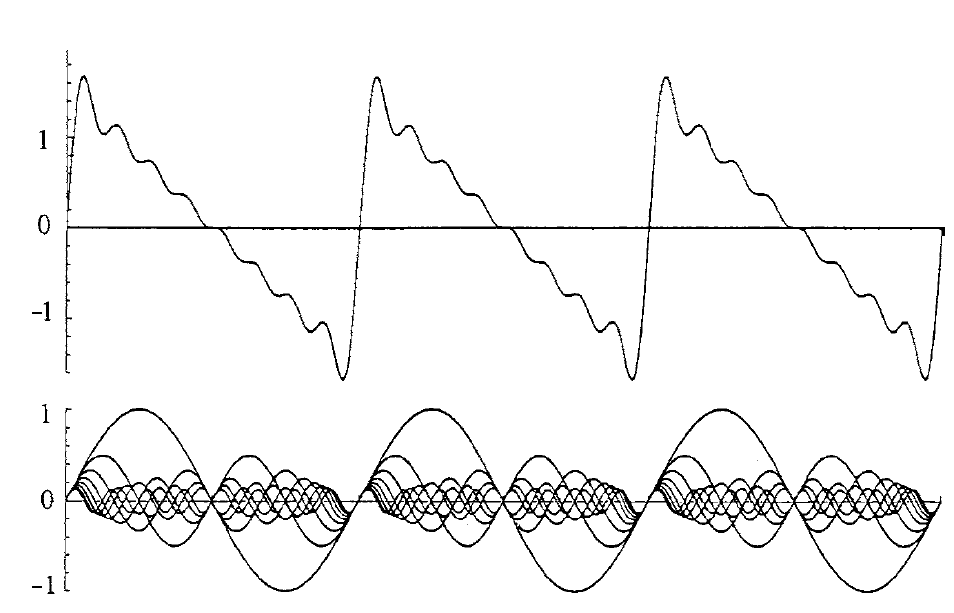
• Fourier transform
어떠한 함수든 sin과 cos의 적분으로 기술이 가능하다.
\begin{equation}
\begin{aligned}
& f(x)=\int_{-\infty}^{\infty} g(\alpha) e^{i \alpha x} d \alpha, \\
& g(\alpha)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(x) e^{-i \alpha x} d x
\end{aligned}
\end{equation}
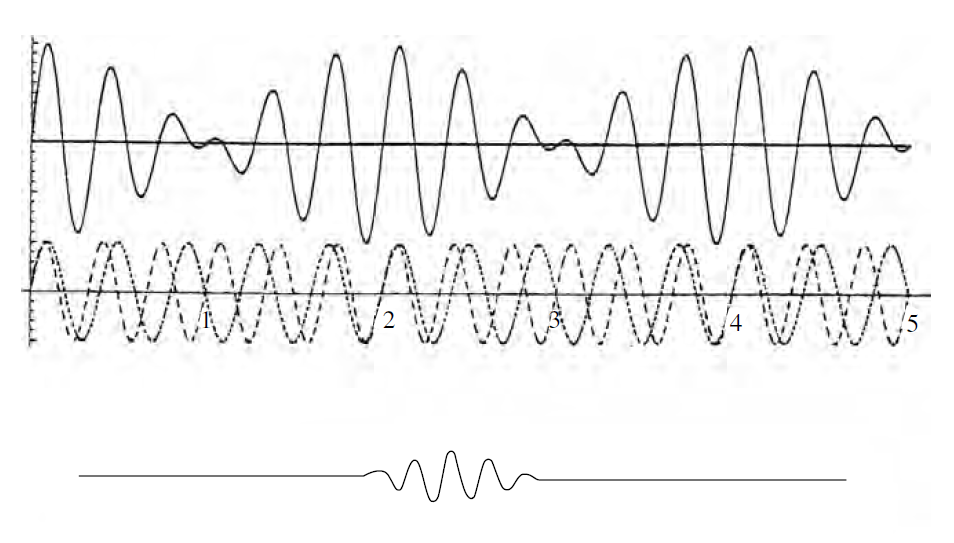
결론: 다양한 운동량($k$)을 가진 파동을 많이 중첩할수록 위치의 불확정도는 낮아진다.
2.2 Schrödinger의 파동방정식(Schrödinger's wave equation)
2.2.1 The Wave Equation
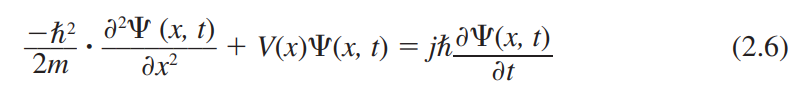
$\Psi(x, t)$: 파동함수(the wave function)
$V(x)$ : 포텐셜 에너지(the potential function)
$m$ : 질량(the mass)
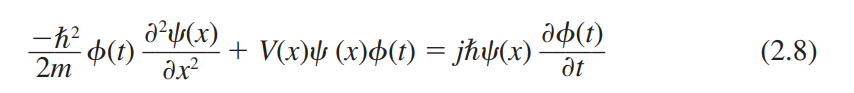
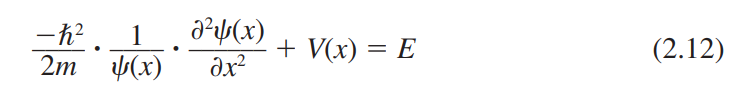
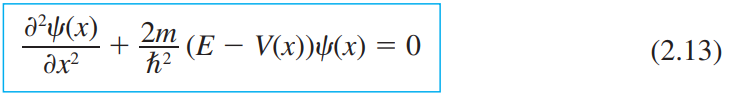
고전 1차원 파동 방정식은 다음과 같이 주어진다.
$$
\frac{\partial^2 u}{\partial x^2}=\frac{1}{v^2} \frac{\partial^2 u}{\partial t^2}
$$
$u(x, t)$는 다음과 같이 분리하자.
$$
u(x, t)=\psi(x) e^{-i \omega t}
$$
이것을 대입하면,
$$
\frac{d^2 \psi}{d x^2}+\frac{\omega^2}{v^2} \psi(x) = 0
$$
다음을 고려하면
$\omega = 2\pi f$, $v = f \lambda$
$$
\frac{d^2 \psi}{d x^2}+\frac{4 \pi^2}{\lambda^2} \psi(x)=0
$$
에너지는 다음과 같이 주어진다.
$$
E=\frac{p^2}{2 m}+U(x)
$$
여기서 $U(x)$는 포텐셜 에너지이다.
그러면 운동량은 다음과 같이 표현된다.
$$
p=\sqrt{2 m(E-U(x))}
$$
De Broglie 물질파의 파장은 다음과 같이 표현된다.
$$
\lambda=\frac{h}{p}=\frac{h}{\sqrt{2 m(E-U(x))} }
$$
이것을 대입하면, 다음의 Schrödinger 방정식을 얻는다.
$$\frac{d^2 \psi}{d x^2}+\frac{2 m}{\hbar^2}(E - U(x)) \psi(x) = 0 $$
2.2.2 Physical Meaning of the Wave Function
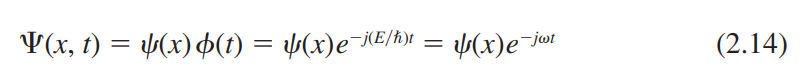
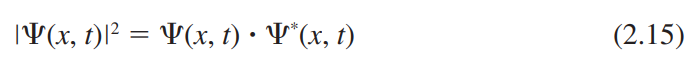
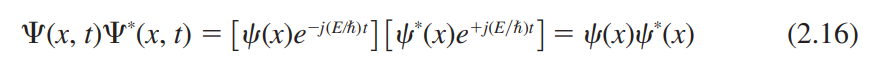
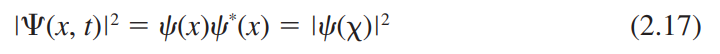$\left|\Psi(x,t)\right|^2$ : 확률밀도 함수(probability density function)
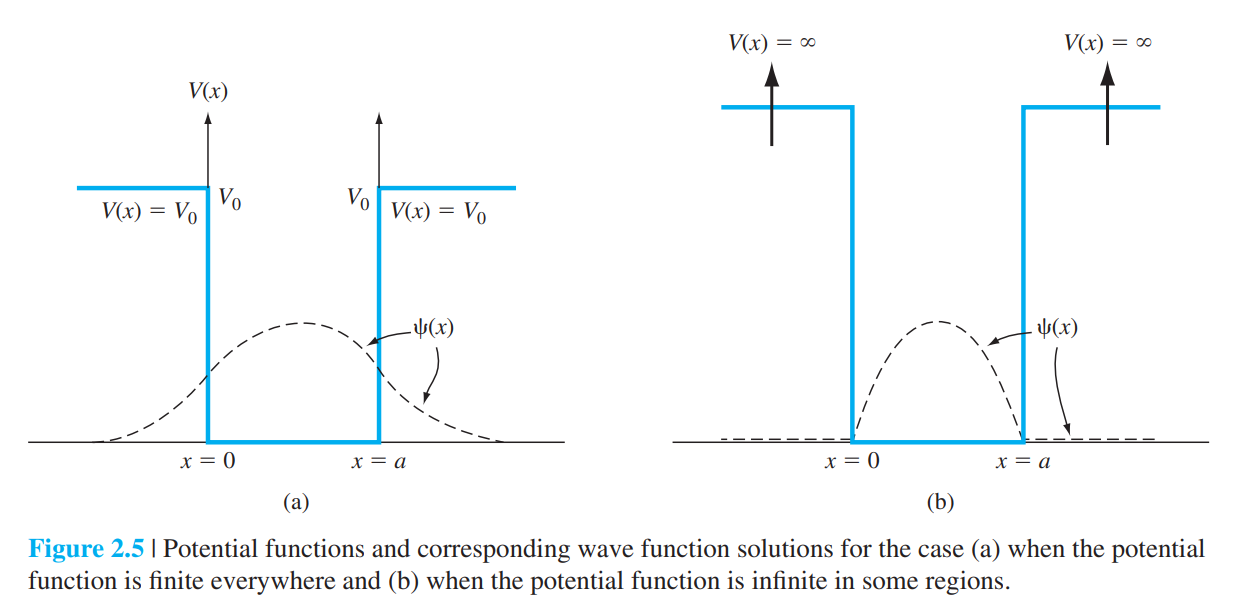
2.2.3 경계조건
• 규격화(normalization)
2.3 Schrödinger 방정식의 적용
2.3.1 자유공간에서의 전자자유공간에 있는 전자는 모든 공간에서 동일한 값을 가진 포텐셜 에너지 내에 있는 것으로 간주될 수 있다. 그러한 포텐셜 에너지중에서 가장 다루기 쉬운 포텐셜 에너지는 아래와 같이 모든 공간에서 0의 값을 가진 포텐셜이다. $$ U(x) = 0 \qquad (-\infty < x < \infty) $$ 위 포텐셜에너지 하에서 Schrödinger 방정식은 다음과 같이 주어진다. $$ \frac{\partial^2 \psi(x)}{\partial x^2}+\frac{2 m E}{\hbar^2} \psi(x)=0 $$ 위 방정식의 해는 다음과 같이 주어진다. $$ \psi(x) = A e^{ikx} + B e^{-ikx} $$ 여기서 $k$는 다음과 같이 주어진다. $$ k=\sqrt{\frac{2 m E}{\hbar^2}} \qquad (2.21)$$ (2.7)식에서 처럼 완전한 해 $\Psi(x, t)$ 는 $\psi(x)$와 $\phi(t)$의 곱으로서 다음과 같이 얻어진다. $\phi(t)$은 다음과 같이 얻어지고, $$ \phi(t)=e^{-i(E / \hbar) t}=e^{-i \omega t}$$ $\Psi(x, t)$은 다음과 같이 얻어진다. $$ \Psi(x, t) = A e^{i(k x-\omega t)} + B e^{-i(k x+\omega t)} $$ 이 식의 형태는 파동과 동일하다. 위 식 우변의 첫째항은 $+x$로 진행하는 파동을, 두 번째항은 $-x$로 진행하는 파동을 의미한다. $+x$ 방향으로만 진행하는 파동을 가정하면, $\Psi(x, t)$는 다음과 같이 주어진다. $$ \Psi(x, t)=A e^{i(k x-\omega t)} $$ 여기서 $k$는 다음과 같이 운동량 $p$와 관련이 있다. $$k=\sqrt{\frac{2 m E}{\hbar^2}}=\sqrt{\frac{p^2}{\hbar^2}}=\frac{p}{\hbar}$$ 그러면 전자를 입자라고 간주했을 때의 운동량은 다음과 같이 주어진다. $$p=\hbar k$$ 전자를 파동으로 간주할 때의 파장은 De Broglie 가설에 의하면 다음과 같이 주어진다. $$ \lambda=\frac{h}{p}=\frac{2 \pi \hbar}{p} =\frac{2 \pi}{k} $$
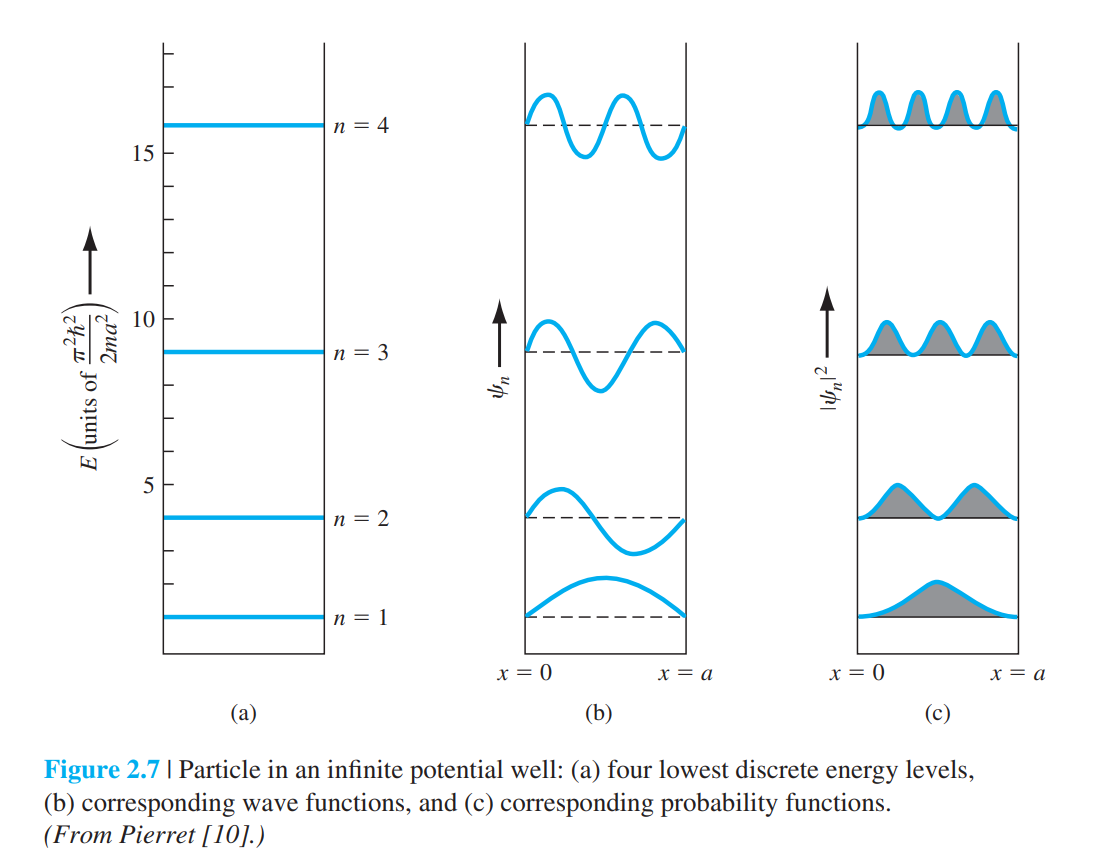
2.3.2 무한 포텐셜 우물
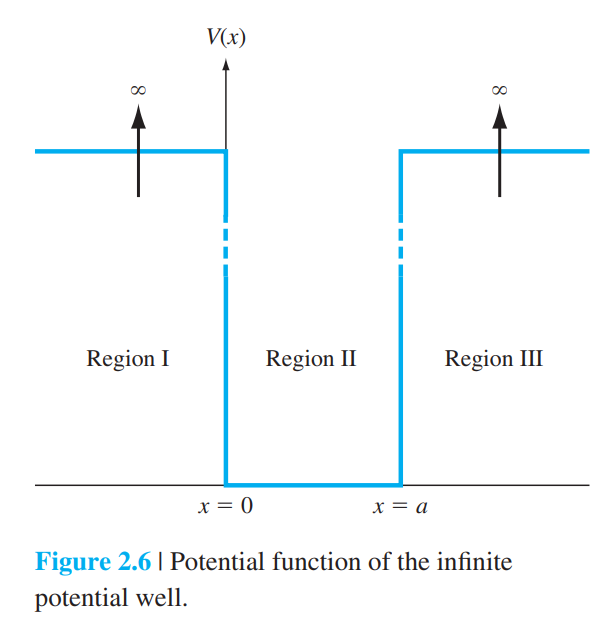
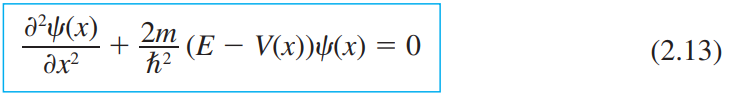
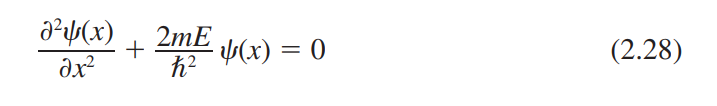
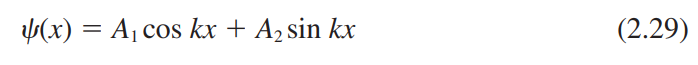
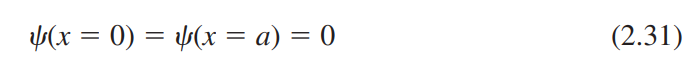
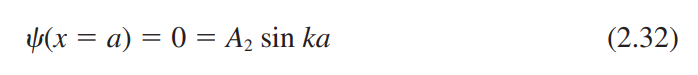
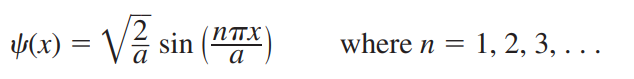
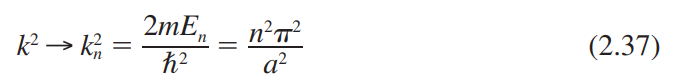
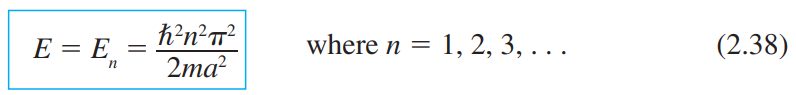
2.3.3 계단 포텐셜
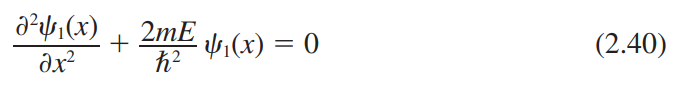
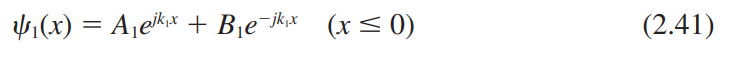
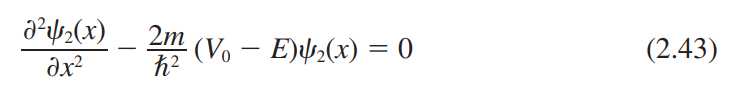
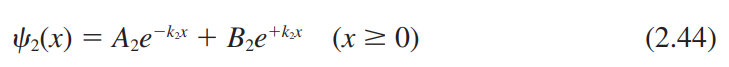
반사 계수(Reflection coefficient, R)
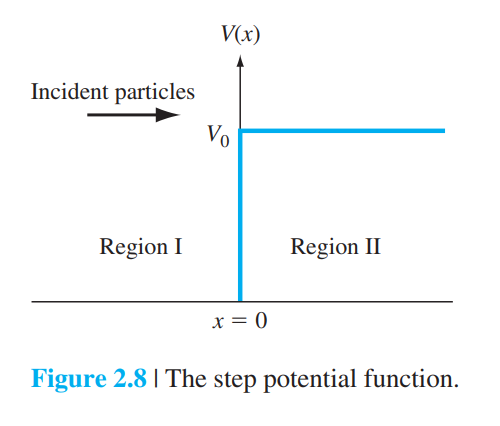
2.3.4 포텐셜 장벽과 투과(The Potential Barrier and Tunneling)
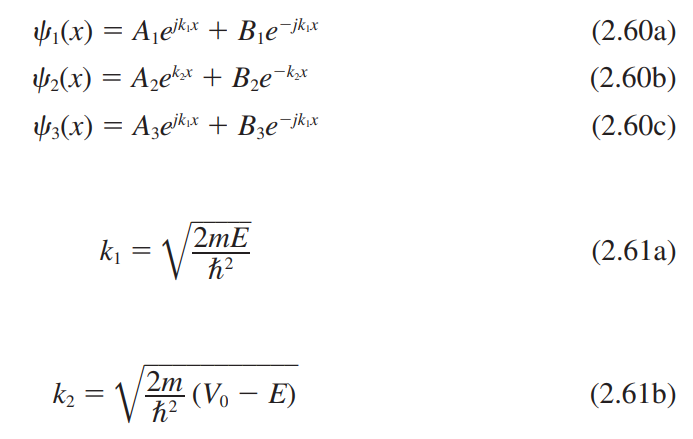
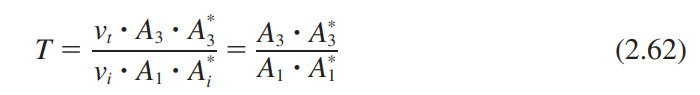
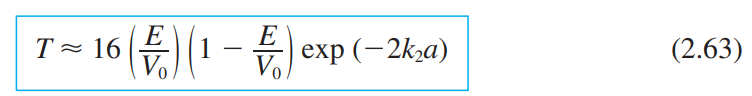
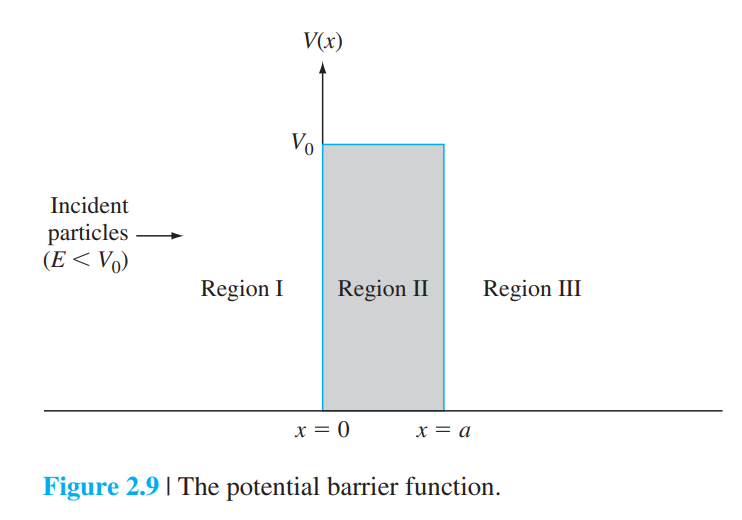
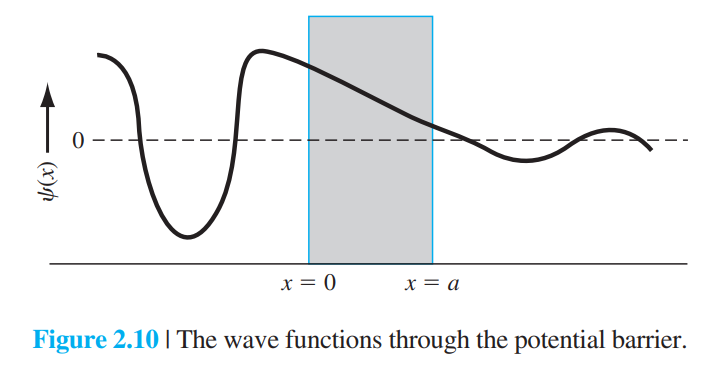
2.4 Schrödinger 방정식을 원자에 적용
2.4.1 1 전자 원자(The One-Electron Atom)
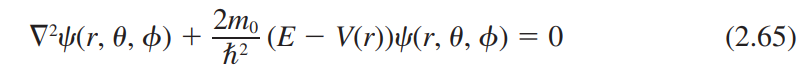
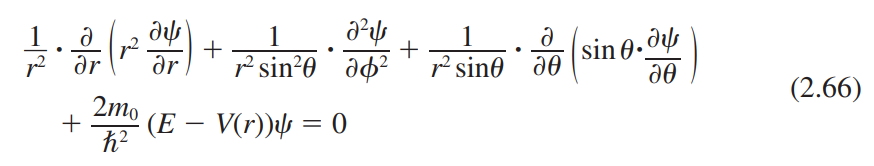
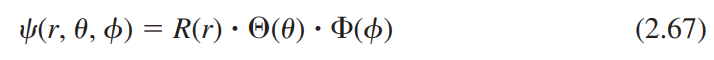
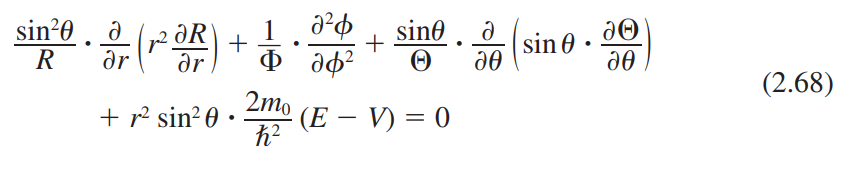
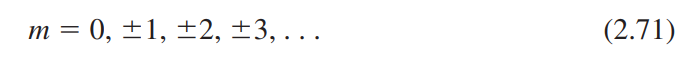
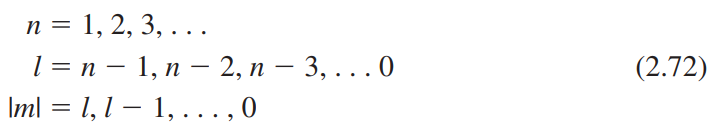
수소원자에서 전자의 파동함수는 다음과 같이 표기한다.
$$\psi_{nlm}=R_{nl}(r)Y_{lm}(\theta, \phi)$$
여기서 $n$, $m$, $l$은 양자수를 의미한다.
$Y_{lm}(\theta, \phi)$ : spherical harmonics
$R_{nl}(r)$ : radial wave functions
$L_{n+l}^{2l+1}$ : associated Laguerre polynomials
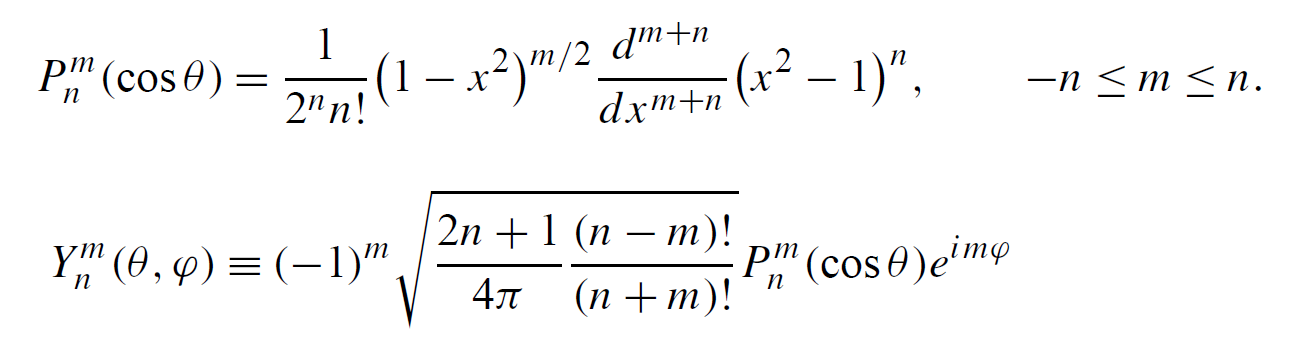
$P_n^m(\cos\theta)$ : associated Legendre functions
$$\psi_{100}=\frac{1}{\sqrt{\pi}} \left( \frac{1}{a_0}\right)^{3/2} e^{-r/a_0}$$
$$a_0=\frac{4\pi \epsilon_0 \hbar^2}{m_0 e^2}= 0.529 Å $$
규격화
\begin{equation}
\begin{aligned}
& \int\int\int \left|\psi_{nlm} (r,\theta,\phi)\right|^2 dV =1 \\
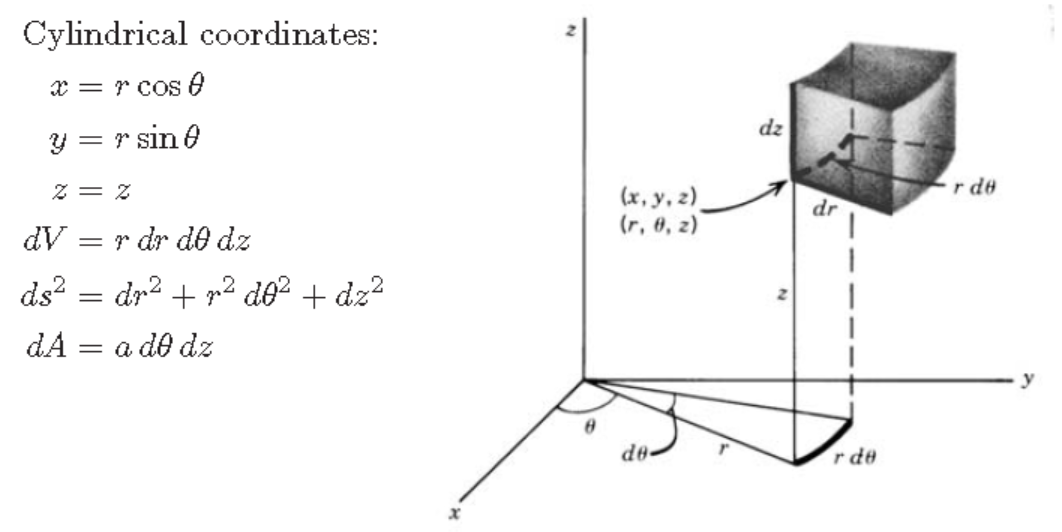
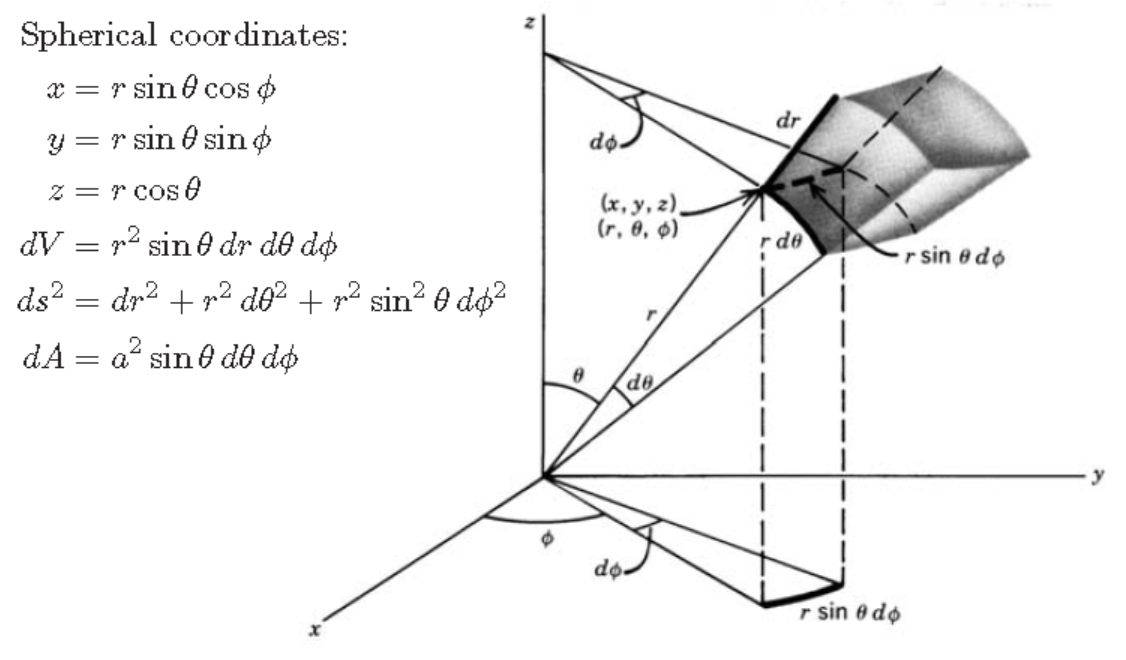
& \int_0^{2\pi} \int_0^\pi \int_0^\infty \left| \psi_{nlm}(r,\theta,\phi) \right|^2 (dr)(rd\theta)(r\sin\theta d\phi)=1 \\
& \int_0^{2\pi} \int_0^\pi \int_0^\infty \left|R_{nl}(r)Y_{lm}(\theta,\phi) \right|^2 r^2 \sin\theta dr d\theta d\phi = 1
\end{aligned}
\end{equation}
여기서 spherical harmonics $Y_{lm}(\theta,\phi)$는 다음과 같이 규격화되어 있음.
$$ \int_0^{2\pi} \int_0^\pi \left|Y_{lm}(\theta,\phi) \right|^2 \sin\theta d\theta d\phi = 1 $$
그래서 다음이 성립한다.
\begin{equation}
\begin{aligned}
\int_0^\infty \left|R_{nl}(r)\right|^2 r^2 dr = 1
\end{aligned}
\end{equation}
위치 $r$에서 전자를 발견할 확률
$P_{nl}(r)$을 위치 r에서 전자를 발견할 확률밀도라고 두면
$$P_{nl}(r) = \left| R_{nl}(r)\right|^2 r^2 $$
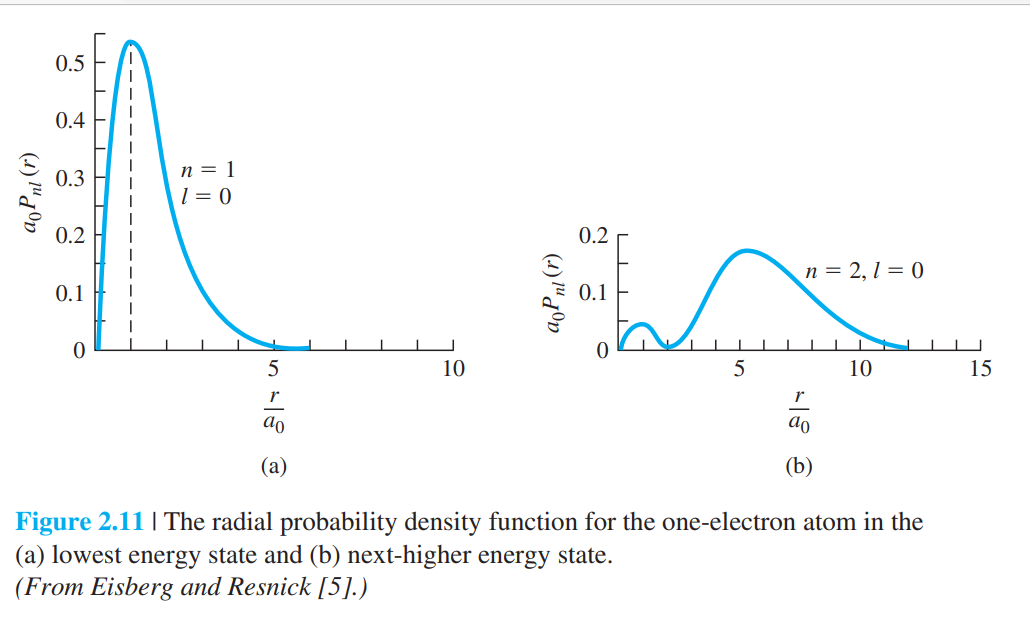
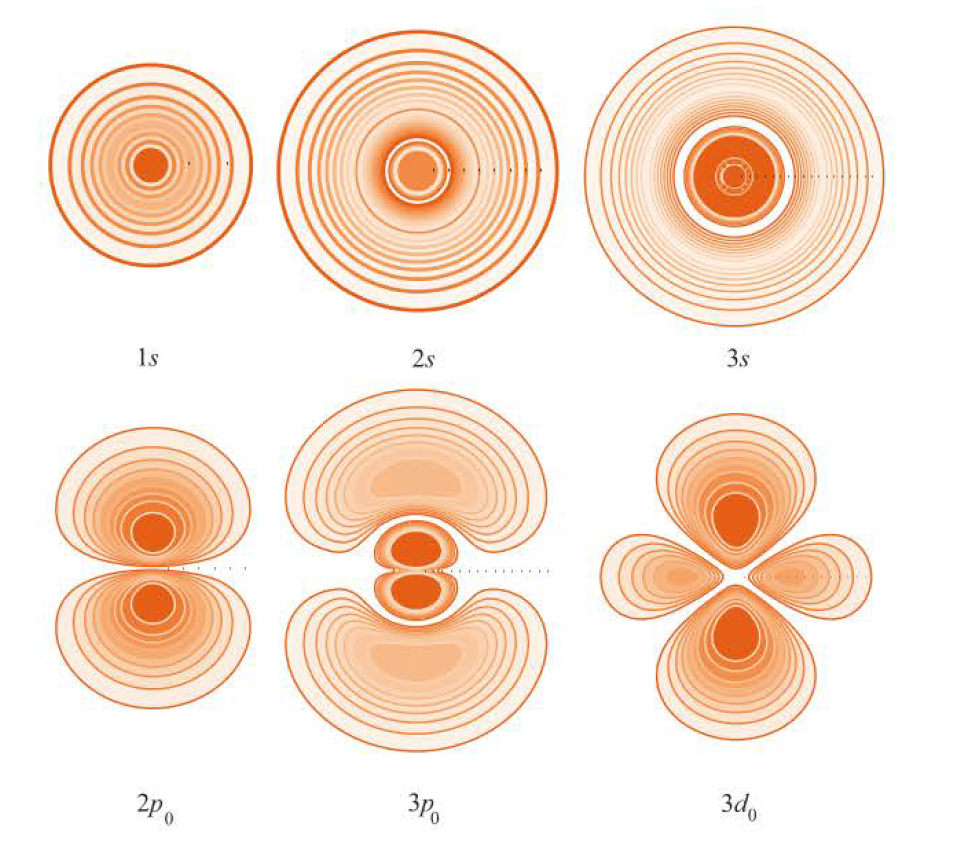
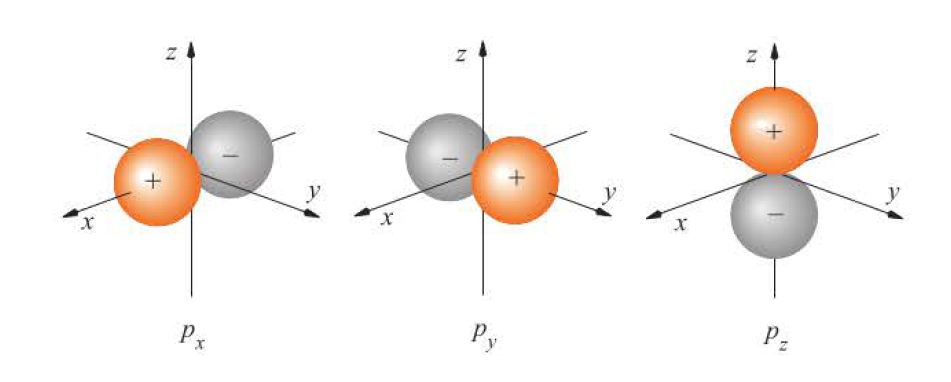
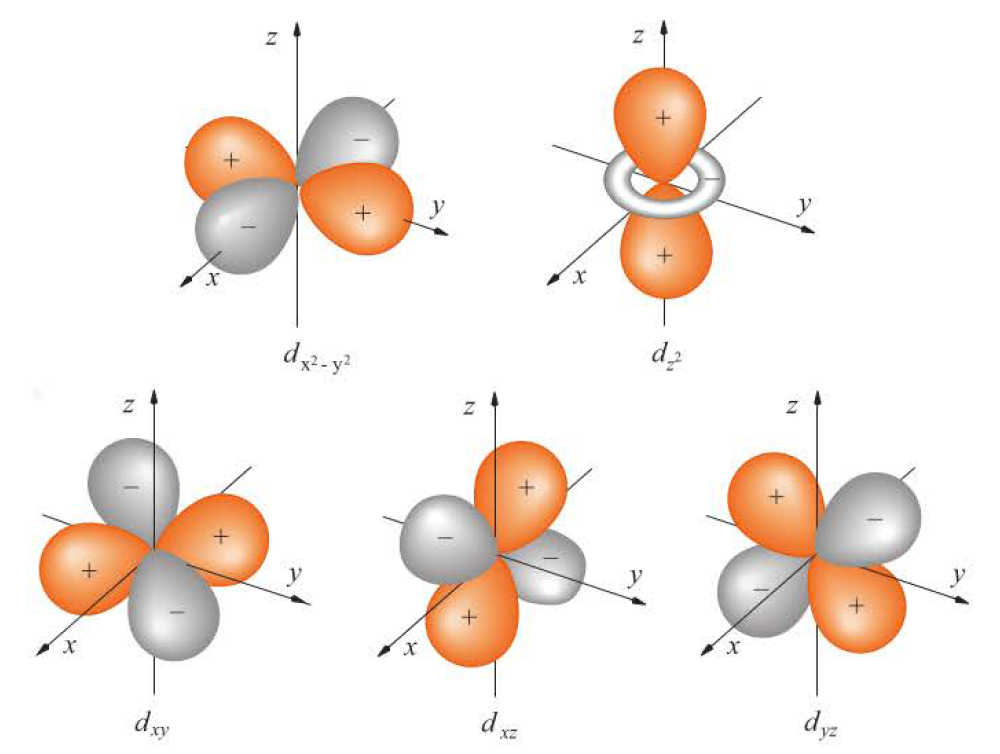
Quantum chemistry (McQuarrie, Donald A.) 참조
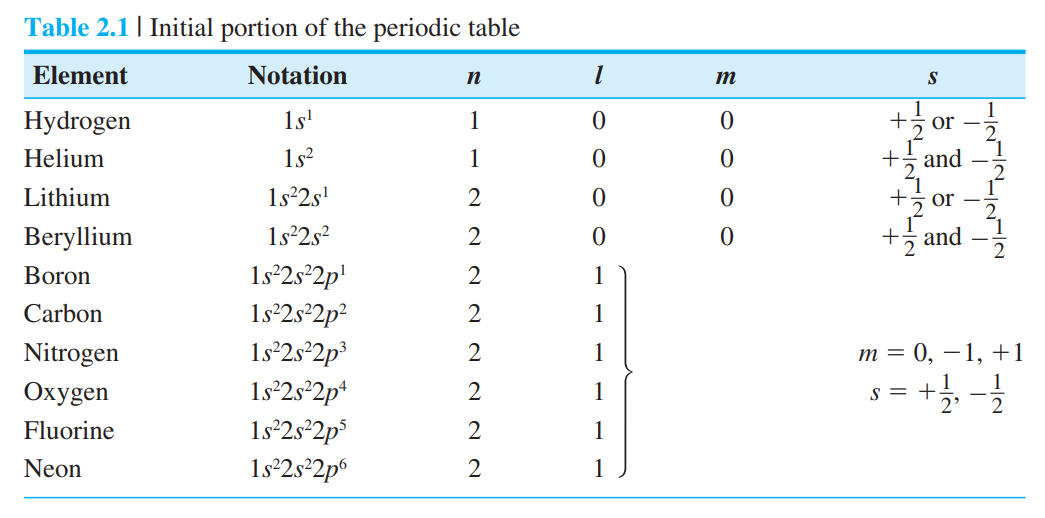
2.4.2 The Periodic Table
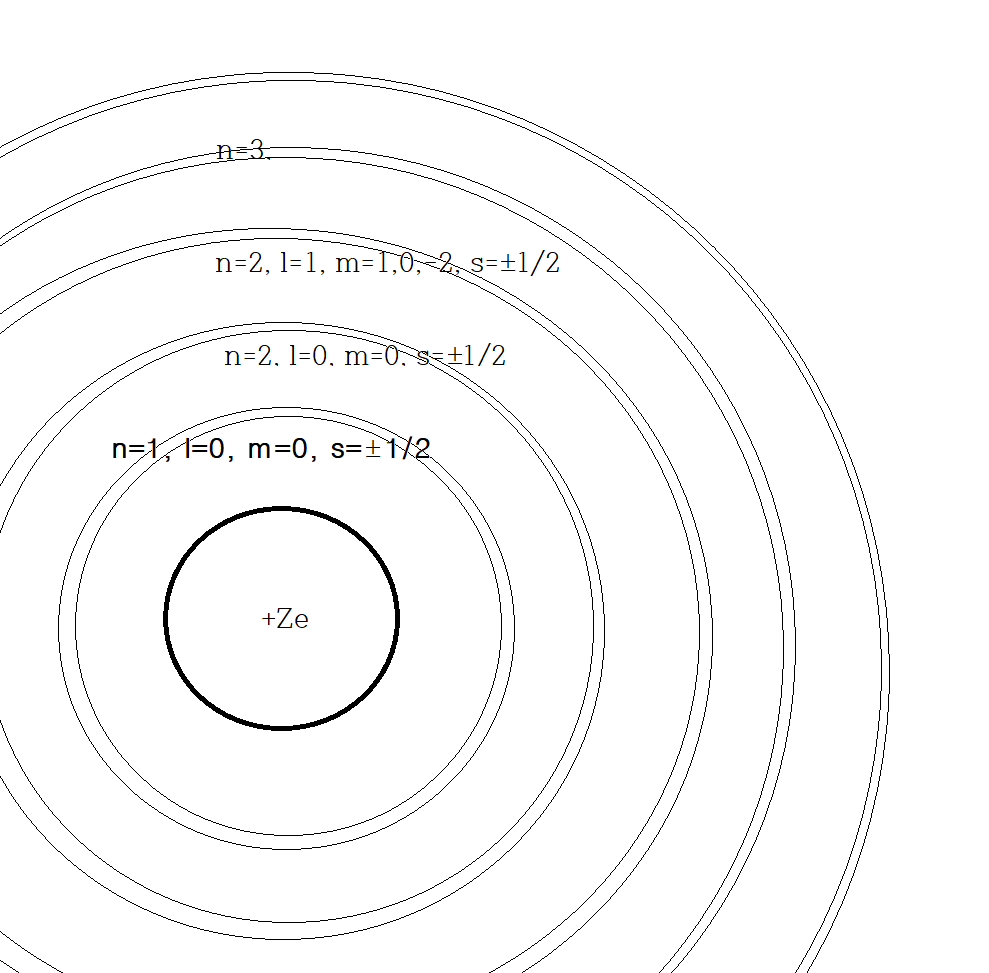
전자의 추가 양자수 : 스핀 $s= + \frac{1}{2}$ or $-\frac{1}{2}$
원자내의 전가가 가지는 양자수 : $n, l, m, s$
Pauli의 배타원리(Pauli's exclusion principle)
: 두 개의 전자가 같은 양자 상태에 있을 수 없다.
| $n$ | $l$ | $m$ | orbital |
| 1 | 0 | 0 | $1s$ |
| 2 | 0 | 0 | $2s$ |
| 1 | 1, 0, -1 | $2p_x$, $2p_y$, $2p_z$ | |
| 3 | 0 | 0 | $3s$ |
| 1 | 1, 0, -1 | $3p_x$, $3p_y$, $3p_z$ | |
| 2 | 2, 1, 0, -1, -2 | $3d_{x^2-y^2}$, $3d_{z^2}$, $3d_{xy}$, $3d_{yz}$, $3d_{zx}$ |
주의. 위 표에서 나타난 양자수 $m$과 궤도(orbital)가 1대1 대응되는 것은 아니고,
다만 양자수 $m$의 수만큼 궤도가 존재한다는 것을 표는 보여준다.
실제로 $p_x$와 $p_y$ 궤도는 다음과 같이 양자수 $m$인 파동함수들의 결합으로 이루어진다.
$$Y_{p_x} \sim Y_{1,1} + Y_{1,-1}$$
$$Y_{p_y} \sim Y_{1,1} - Y_{1,-1}$$
