2. 정전기학과 전기장

2.1 전하(electric charge)

• 전하의 정의
전하(charge): 물체가 전기를 띄게하는 특성.
물체가 전기를 띄게 되는 것을 대전된다고(charged) 말함.

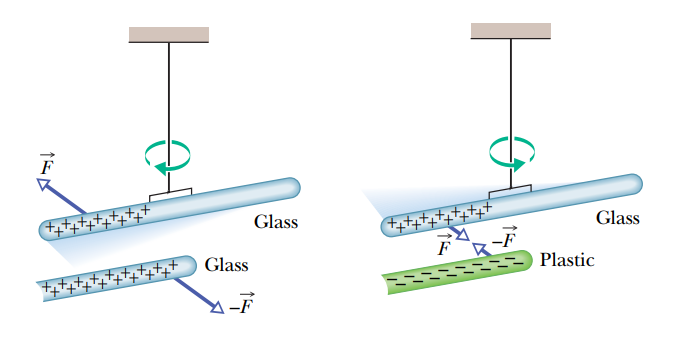
• 전하의 종류
전하는 양전하와 음전하 이 두 종류의 전하가 있다.
보통 전하를 표시할때 알파벳 $q$로 표시하고, 전하의 량인 전하량의 단위는 C(Coulomb) 이라고 한다. 예를 들어 양전하는 +3 C, 음전하는 -2 C 이런 식으로 표시한다.
현재 양전하와 음전하의 최소단위는 잘 알려져 있다. 물질을 이루는 최소단위인 원자는 원자핵과 전자로 이루어져있으며, 핵은 양성자와 중성자로 이루어져있다. 전자와 양성자는 음전하와 양전하의 최소량을 지닌 입자들이며, 그들의 전하량은 각각 다음과 같이 표현된다.
$-e=-1.602\times 10^{-19}$ C
$+e=1.602\times 10^{-19}$ C
여기서 $e$는 전자 1개의 전하량이라는 뜻이며, 양성자의 전하량 역시 전자의 전하량과 크기는 동일하다.
• 전하의 양자화
임의 물체에 대한 전하량은 최소량인 $e$의 정수배로 주어진다.
• 전하의 보존
전하량은 보존된다.

2.2 Coulomb의 법칙

• 두 점전하 사이의 힘
- 전하의 종류 : 양전하, 음전하
- 두 점전하 사이에는 서로를 향하여 끌어당기거나 밀어내는 힘이 있다.
- 두 점전하가 같은 종류이면 서로 밀어내고, 다른 종류이면 끌어당긴다.
- 그 힘의 크기는 두 점전하의 전하량을 곱한값이 비례하고, 두 점전하사이의 거리의 제곱에 반비례한다.
두 점전하 사이의 힘은 다음과 같은 수식으로 정리되는데 이것을 Coulomb의 법칙이라고 한다.
점전하1과 점전하2가 전기적 상호작용을 할때 전하1이 전하2로부터 받는 힘 $\vec{F}_1$은 다음과 같이 주어진다. $$ \vec{F}_1 = \frac{1}{4\pi\varepsilon_0}\frac{q_1 q_2}{r_{12}^2} \hat{r}_{12} = \frac{1}{4\pi\varepsilon_0}\frac{q_1 q_2}{r_{12}^2} \frac{\vec{r}_{12}}{r_{12}}$$ 위에서 $q_1$과 $q_2$는 각각 점전하1과 점전하2의 전하량
$r_{12}$는 두 점전하 사이의 거리
$\vec{r}_{12}$은 점전하2에서 점전하1로 향하는 벡터
$\hat{r}_{12}$은 점전하2에서 점전하1로 향하는 단위 벡터이다.
$\varepsilon_0(진공의 유전율, 誘電率) = 8.854\times 10^{-12}$ C$^2$/N $\cdot$ m$^2$
$\frac{1}{4\pi\varepsilon_0} = 8.9874\times 10^9$ N $\cdot$ m$^2$/C$^2$
• 전하 무리로부터 점전하가 받는 힘
만약 $N$개의 점전하가 있다면 그 중에 $i$번째 전하가 받는 힘은 다음과 같이 주어진다. \begin{eqnarray} \vec{F}_i = q_i \sum_{j \neq i}^N \frac{1}{4\pi\varepsilon_0}\frac{q_j}{r_{ij}^2} \hat{r}_{ij} \end{eqnarray} (예제)
$q_1 = -1$ C, $q_2 = +2$ C, $q_1 = +3$ C 일때, 전하 $q_2$가 받는 힘은?
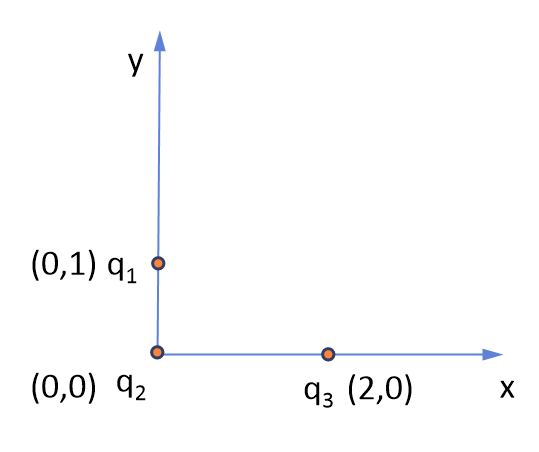
\begin{equation} \begin{aligned} \vec{F}_2 &= \vec{F}_{21} + \vec{F}_{23}\\ & = \frac{1}{4 \pi \epsilon_0} \frac{(-1)(+2)}{1^2} \hat{j} + \frac{1}{4 \pi \epsilon_0} \frac{(+2)(+3)}{2^2} (-\hat{i}) \end{aligned} \end{equation} Python 풀이
import math
import numpy as np
C_1_4pe = 8.9874*10**9
r1 = np.array([0,1])
r2 = np.array([0,0])
r3 = np.array([2,0])
q1 =-1
q2 = 2
q3 = 3
F21 = C_1_4pe * q2*q1 * (r2-r1) /np.linalg.norm(r2-r1)**3
F23 = C_1_4pe * q2*q3 * (r2-r3) /np.linalg.norm(r2-r3)**3
F2 = F21 + F23
print(F2)
• 전하 분포로 부터 점전하가 받는 힘
전하밀도 $\rho(\vec{r})$와 $\sigma(\vec{r})$로 정의되는 전하분포로부터 전하 $q$가 받는 힘은 다음과 같이 주어진다. \begin{equation} \vec{F}_q=\frac{q}{4 \pi \epsilon_0} \int_V \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \rho\left(\vec{r}^{\prime}\right) d v^{\prime}+\frac{q}{4 \pi \epsilon_0} \int_S \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \sigma\left(\vec{r}^{\prime}\right) d a^{\prime} \end{equation} 전하밀도 $\rho(\vec{r})$와 $\sigma(\vec{r})$로 정의되는 전하분포와 $N$개의 점전하로부터 전하 $q$가 받는 힘은 다음과 같이 주어진다. \begin{equation} \begin{aligned} \vec{F}= & \frac{q}{4 \pi \epsilon_0} \sum_{i=1}^N q_i \frac{\vec{r}-\vec{r}_i}{\left|\vec{r}-\vec{r}_i\right|^3}\\ +&\frac{q}{4 \pi \epsilon_0} \int_V \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \rho\left(\vec{r}^{\prime}\right) d v^{\prime} + \frac{q}{4 \pi \epsilon_0} \int_S \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \sigma\left(\vec{r}^{\prime}\right) d a^{\prime} \end{aligned} \end{equation} (2-1)

2.3 전기장

두 전하사이의 힘은 Coulomb법칙으로 기술될 수 있지만, 거리상으로 떨어져 있는 두 전하사이의 힘을 개념적으로 설명하기 위하여 전기장의 개념이 도입된다. 즉, 전하가 존재하면 그 주위에는 전기장(냄새)이 펼쳐지고, 그 공간에 다른 전하가 놓이면 그 위치에 있던 전기장에 의해 즉각 반응한다는 식으로 Coulomb법칙을 설명할 수 있다. 전기장은 정량적으로 다음과 같이 정의된다. \begin{equation} \vec{E}=\lim _{\boldsymbol{q} \rightarrow 0} \frac{\vec{F}_q}{q} \end{equation} 특정 전하분포가 만드는 전기장을 측정하기위한 테스트 전하로 위 식에서 처럼 전하 $q$를 도입할 수 있으며, 전기장은 전하 $q$가 특정전하분포로 부터 받는 힘을 $q$로 나눠줘서 얻는다. 이때 특정 전하분포 전기장은 테스트 전하 $q$와 무관한 것이며, 전하 $q$는 단지 전기장을 측정하기 위한 수단으로 도입되었기 때문에, $q$가 그 전하분포에 변형을 주어서는 안될것이다. 그래서 $q$는 위 전기장의 정의에 나와 있는 것 처럼 최소화되어야 한다.
$N$개의 점전하와 $\rho(\vec{r})$와 $\sigma(\vec{r})$로 정의되는 전하분포가 위치 $\vec{r}$에 만드는 전기장은 식 (2-1)을 $q$로 나누면 얻어진다. \begin{equation} \begin{aligned} \vec{E}= & \frac{1}{4 \pi \epsilon_0} \sum_{i=1}^N q_i \frac{\vec{r}-\vec{r}_i}{\left|\vec{r}-\vec{r}_i\right|^3}\\ +&\frac{1}{4 \pi \epsilon_0} \int_V \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \rho\left(\vec{r}^{\prime}\right) d v^{\prime} + \frac{1}{4 \pi \epsilon_0} \int_S \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \sigma\left(\vec{r}^{\prime}\right) d a^{\prime} \end{aligned} \end{equation}

2.4 전기포텐셜

전기장의 수식 표현에는 공통적으로 다음 항이 있다. $$\frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}$$ 위 항에 curl을 취해 보면, 다음 결과를 얻는다. \begin{equation} \begin{aligned} \nabla \times \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} &=\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} \nabla \times\left(\vec{r}-\vec{r}^{\prime}\right) \\ &+\left(\nabla \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right) \times\left(\vec{r}-\vec{r}^{\prime}\right) \end{aligned} \end{equation} (2-2) (주의) 위 식에서 curl은 $r$에 대한 미분이지, $r'$에 대한 미분이 아니다.
(참고) 위 식에서 curl을 취할 때 항이 2개가 되는 것은, 일반적으로 두 항의 곱을 미분할 때, 항이 2개가 되는 것과 같은 원리이다.
$$예: \quad \frac{d(AB)}{dx}=\frac{dA}{dx}B + A\frac{dB}{dx}$$
식 (2-2) 항들을 계산해 보면 \begin{equation} \nabla \times\left(\vec{r}-\vec{r}^{\prime}\right)=0 \end{equation} \begin{equation} \nabla \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}=-3 \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^5} \end{equation} 결과적으로 다음이 성립한다. \begin{equation} \nabla \times \frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}=0 \end{equation} 이것은 다음을 의미한다. \begin{equation} \nabla \times \vec{E}=0 \end{equation} 다음 식과 비교하면 \begin{equation} \nabla \times \nabla \varphi(\vec{r})=0 \end{equation} 전기장은 다음과 같이 어떤 스칼라함수 $\varphi(\vec{r})$ 의 gradient로 정의할 수 있다는 것을 알 수 있다. \begin{equation} \vec{E}(\vec{r})=-\nabla \varphi(\vec{r}) \end{equation} 이 스칼라함수 $\varphi(\vec{r})$를 전기 포텐셜(electric potential)이라고 한다. 정전기학의 주된 관심사는 전하분포가 주어질 때, 공간에서의 전기장을 구하는 것이다. 그러나 전기장은 벡터량이기 때문에 구하는데 좀 번거로움이 있다. 전기 포텐셜은 스칼라 함수이기 때문에 상대적으로 구하기 쉽다. 그래서 일반적으로 전기장을 바로 구하기 보다는 먼저 전기 포텐셜을 구한 다음에 위 식을 적용하여 전기장을 구하는 방식을 취한다. 원점에 있는 점전하 $q_1$이 위치 $r$에 만든 전기 포템셜은 다음과 같이 주어진다. \begin{equation} \varphi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \frac{q_1}{\left|\vec{r}-\vec{r}_1\right|} \end{equation} $N$개의 점전하와 $\rho(\vec{r})$와 $\sigma(\vec{r})$로 정의되는 전하밀도에 의한 전기 포텐셜은 다음과 같이 주어진다. \begin{equation} \begin{aligned} \varphi(\vec{r})= & \frac{1}{4 \pi \epsilon_0} \sum_{i=1}^N \frac{q_i}{\left|\vec{r}-\vec{r}_i\right|}+\frac{1}{4 \pi \epsilon_0} \int_V \frac{\rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d v^{\prime} \\ & +\frac{1}{4 \pi \epsilon_0} \int_S \frac{\sigma\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d a^{\prime} \end{aligned} \end{equation} • 등 포텐셜 면
등 포텐셜 면: 전기장에 수직

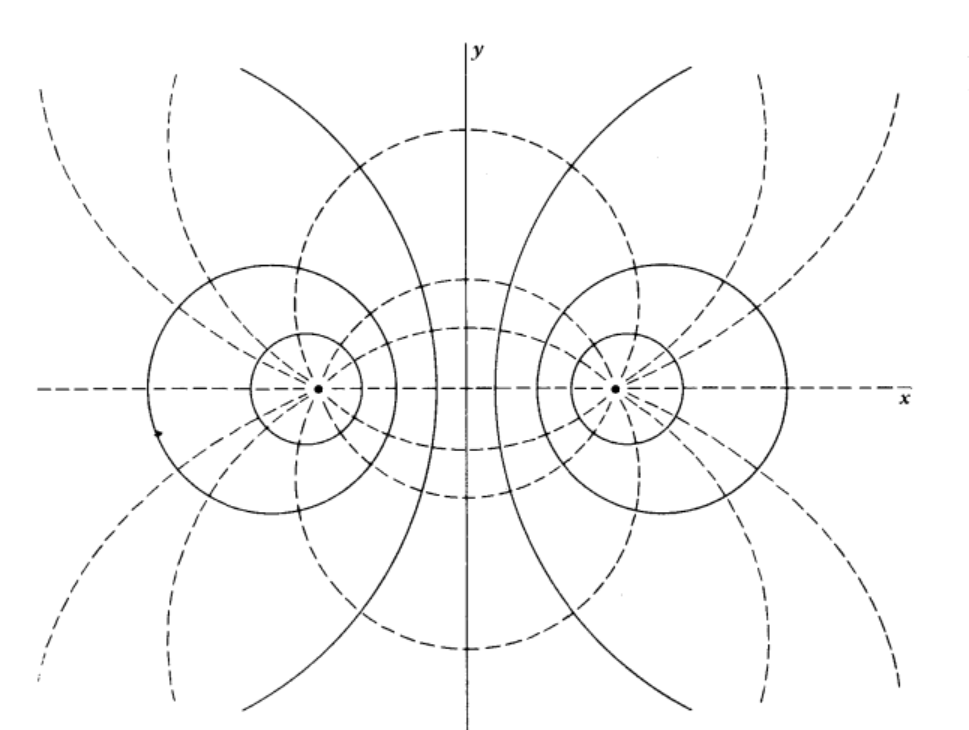
• 주어진 전기장으로부터 전기 포텐셜 얻기
\begin{equation} \begin{aligned} \int_{\text {기준점}}^\vec{r} \vec{E}\left(\vec{r}^{\prime}\right) \cdot d \vec{r}^{\prime} &= -\int_{\infty}^\vec{r} \nabla' \varphi \cdot d \vec{r}^{\prime} = -\int_{\infty}^\vec{r} d \varphi \\ &= -(\varphi(\vec{r}) - 0) \end{aligned} \end{equation} \begin{equation} \begin{aligned} \varphi(\vec{r}) = - \int_{\text {기준점}}^\vec{r} \vec{E}\left(\vec{r}^{\prime}\right) \cdot d \vec{r}^{\prime} \end{aligned} \end{equation} 여기서 기준점은 포텐셜이 0이되는 지점을 의미하는데 통상 무한대 지점이 선택된다.
유사하게 포텐셜 에너지는 다음과 같이 얻어진다.
\begin{equation} U(\vec{r})=-\int_{\mathrm{ref}}^{\vec{r}} \vec{F}\left(\vec{r}^{\prime}\right) \cdot d \vec{r}^{\prime} \end{equation}
• 보존장
시점과 종점만 같으면 경로적분이 같음

2.5 도체와 유전체

• 도체
도체에서는 전하의 흐름이 자유롭다. 그래서 약간의 과잉전하가 있어도 이 전하들은 서로간의 척력에 의해 전하들은 도체의 표면에만 분포한다. 정적인 상황에서 도체 내부에는 전하가 존재하지 않는다. 그래서 도체내부의 전기장은 0이고, 도체 외부에만 전기장이 존재한다.
• 유전체
유전체에서는 전하의 흐름이 자유롭지 않고, 그 원자들이 주로 쌍극자를 형성한다. 전기장을 걸면 쌍극자들이 유도되거나, 영구 쌍극자들이 전기장 방향으로 정렬해서, 유전체 내부에서는 (쌍극자)원자들간의 전기장이 발생한다. 그리고 표면에도 유도된 전하들이 존재한다.

2.6 Gauss 법칙

가우스 법칙은 어떤 폐곡면(가우스면)을 통과하는 전기다발은 그 폐곡면내의 들어있는 전하의 전하량 $Q$에 비례한다는 것이다. 이것을 정리하면 다음과 같다. \begin{equation} \oint_s \vec{E} \cdot \hat{n} d a = \frac{Q}{\epsilon_0} \end{equation} 위 식에서 좌변은 전하 $Q$를 둘러싼 폐 곡면을 통과하는 전기다발이다.
전기다발$\Phi_E$의 정의 = 전기장 $\times$ 면적
\begin{equation} \Phi_E = \oint_s \vec{E} \cdot \hat{n} d a = \frac{Q}{\epsilon_0} \end{equation} 가우스 법칙을 증명해보자. 먼저 점전하 $q$가 만드는 전기장은 다음과 같이 주어지고 \begin{equation} \vec{E}(\vec{r})=\frac{q}{4 \pi \epsilon_0} \frac{\vec{r}}{r^3} \end{equation} 그 점전하를 둘러싼 폐곡면을 통과하는 전기다발을 구해보면 아래와 같이 주어진다. \begin{equation} \oint_S \vec{E} \cdot \hat{n} d a=\frac{q}{4 \pi \epsilon_0} \oint_S \frac{\vec{r} \cdot \hat{n}}{r^3} d a \end{equation} (2-3) 여기서 $\int_S \frac{\vec{r} \cdot \hat{n}}{r^3} d a$은 면적 $S$에 대응되는 입체각(solid angle)이다. 위 식은 전 공간에 대한 입체각(solid angle)이다. 전 공간에 대한 입체각은 $4\pi$라는 것이 아래에 증명된다. \begin{equation} \oint_s \frac{\vec{r} \cdot \hat{n}}{r^3} d a=\oint_{s^{\prime}} \frac{\vec{r}^{\prime} \cdot \hat{n}}{r^{\prime 3}} d a^{\prime}=4 \pi \end{equation} 그러면 식 (2-3)은 다음과 같이 되어 가우스 법칙을 증명하게 된다. \begin{equation} \oint_s \vec{E} \cdot \hat{n} d a=\frac{q}{4 \pi \epsilon_0} 4 \pi=\frac{q}{\epsilon_0} \end{equation} 그러면 가우스면 내에 여러 점전하가 있을 때 아래식이 성립하며, \begin{equation} \oint_S \vec{E} \cdot \hat{n} d a=\frac{1}{\epsilon_0} \sum_{i=1}^N q_i \end{equation} 그러면 가우스면 내에 임의의 전하분포가 있을 때 아래식이 성립한다. \begin{equation} \oint_S \vec{E} \cdot \hat{n} d a=\frac{1}{\epsilon_0} \int_{\boldsymbol{V}} \rho d v \end{equation}
• 가우스 법칙의 응용

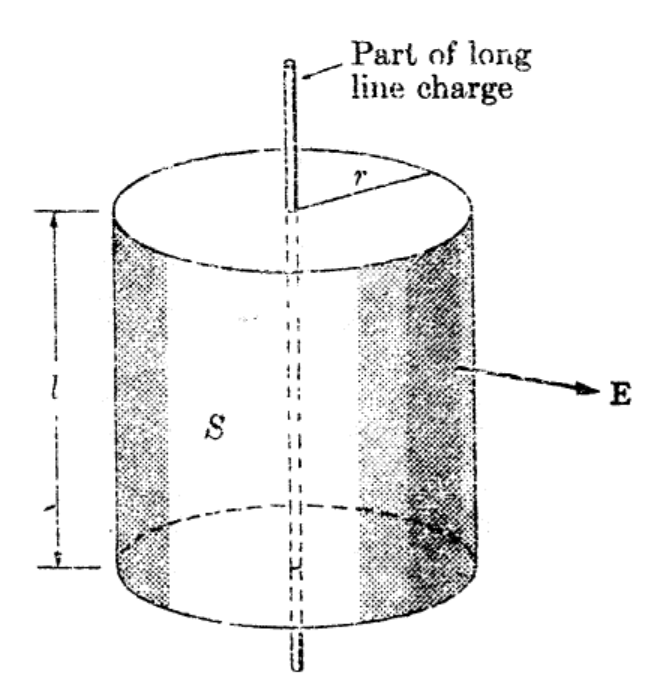
$$ 2 \pi r l E_r=\frac{\lambda l}{\epsilon_0}$$ $$ E_r=\frac{\lambda}{2 \pi \epsilon_0 r} $$ • 도체 표면 근처의 전기장
도체 표면에서 가우스면을 설정하여, 가우스법칙을 적용하면 다음을 얻는다.
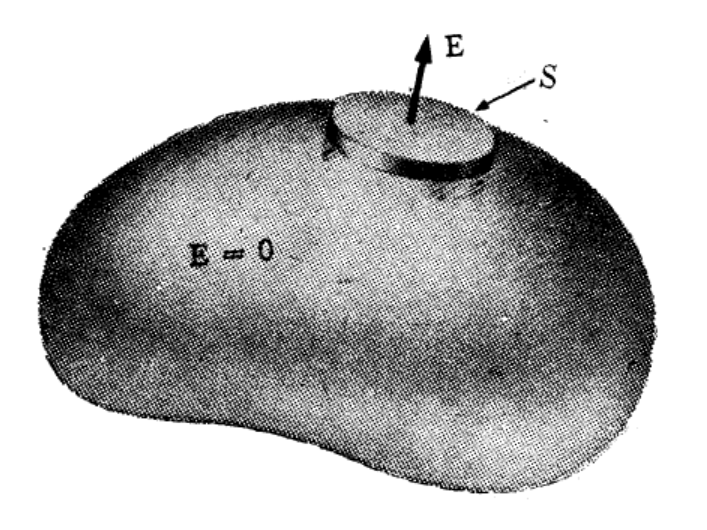
$$ E \Delta S=\left(\frac{\sigma}{\epsilon_0}\right) \Delta S $$ $$ E=\frac{\sigma}{\epsilon_0} $$ • 가우스 법칙의 미분형
Divergence 정리에 의하면 다음이 성립한다.
$$ \int_{\boldsymbol{V}} \nabla \cdot \vec{F} d v = \oint_S \vec{F} \cdot \hat{n} d a $$ 그러면 전기장에 대해서도 다음이 성립하고, 가우스 법칙을 적용하면 다음을 얻는다.
$$ \int_V \nabla \cdot \vec{E} d v = \oint_S \vec{E} \cdot \hat{n} d a =\frac{1}{\epsilon_0} \int_V \rho d v $$ 그러면 다음이 성립한다. $$ \nabla \cdot \vec{E}=\frac{1}{\epsilon_0} \rho $$ 포텐셜의 정의를 이용하면 다음이 성립하는데 아래 방정식을 Poisson 방정식이라고 한다. $$ \nabla^2 \varphi = -\frac{1}{\epsilon_0} \rho $$

2.7 전기 쌍극자

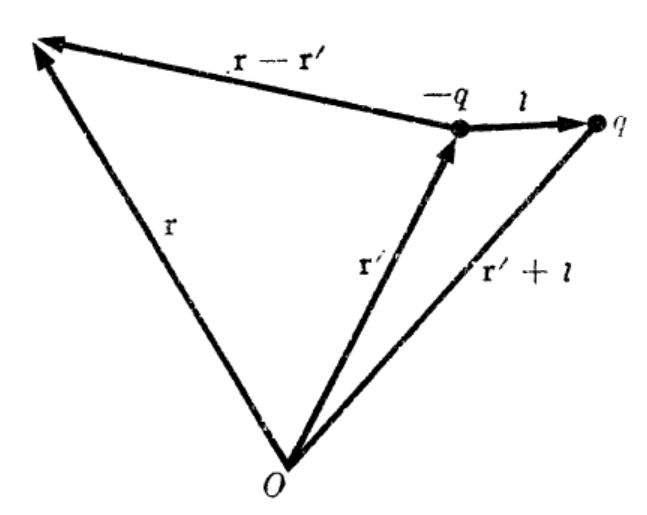
같은 크기 반대부호인 두 전하가 거의 붙어있는 점 형태를 전기쌍극자라고 한다. 전기쌍극자에 의한 전기장과 전기포텐셜을 구해보자. $+q$와 $-q$의 두 전하가 $\vec{l}$ 만큼 떨어져 있을 때, 이 두 점전하에의한 전기장은 다음과 같다. $$ \vec{E}(\vec{r})=\frac{q}{4 \pi \epsilon_0}\left(\frac{\vec{r}-\vec{r}^{\prime}-\vec{l}}{\left|\vec{r}-\vec{r}^{\prime}-\vec{l}\right|^3}-\frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right) $$ 여기서 전기쌍극자가 되려면 $\vec{l}$이 거의 0에 기까운 정도로 근사를 취해야 한다. 그래서 다음과 같이 전개를 한 후에 $\vec{l}$의 고차항을 제거한다. $$ \begin{aligned} \left|\vec{r}-\vec{r}^{\prime}-\vec{l}\right|^{-3} & =\left[\left(\vec{r}-\vec{r}^{\prime}\right)^2-2\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{l}+l^2\right]^{-3 / 2} \\ & =\left|\vec{r}-\vec{r}^{\prime}\right|^{-3}\left[1-\frac{2\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{l}}{\left|\vec{r}-\vec{r}^{\prime}\right|^2}+\frac{l^2}{\left|\vec{r}-\vec{r}^{\prime}\right|^2}\right]^{-3 / 2} \end{aligned} $$ $$ \left|\vec{r}-\vec{r}^{\prime}-\vec{l}\right|^{-3}=\left|\vec{r}-\vec{r}^{\prime}\right|^{-3}\left(1+\frac{3\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{l}}{\left|\vec{r}-\vec{r}^{\prime}\right|^2}+\cdots\right) $$ 그러면 전기장은 다음과 같다. $$ \vec{E}(\vec{r})=\frac{q}{4 \pi \epsilon_0}\left(\frac{3\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{l}}{\left|\vec{r}-\vec{r}^{\prime}\right|^5}\left(\vec{r}-\vec{r}^{\prime}\right)-\frac{\vec{l}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}+\cdots\right) $$ 여기서 $q \vec{l}$ 전기쌍극자 모먼트 $\vec{p}$라고 정의한다. $$ \vec{p}=q \vec{l} $$ 그러면 전기쌍극자 모먼트 $\vec{p}$에 의한 전기장은 다음과 같다. $$ \vec{E}(\vec{r})=\frac{1}{4 \pi \epsilon_0}\left(\frac{3\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{p}}{\left|\vec{r}-\vec{r}^{\prime}\right|^5}\left(\vec{r}-\vec{r}^{\prime}\right)-\frac{\vec{p}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right) $$ 전기쌍극자 모먼트 $\vec{p}$에 의한 전기 포텐셜은 다음과 같다. $$ \varphi(\vec{r})=\frac{q}{4 \pi \epsilon_0}\left[\frac{1}{\left|\vec{r}-\vec{r}^{\prime}-\vec{l}\right|}-\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right] $$ 위 식을 전개 후 $\vec{l}$의 고차항을 제거하면 다음을 얻는다. $$ \varphi(\vec{r})=\frac{q}{4 \pi \epsilon_0} \frac{\left(\vec{r}-\vec{r}^{\prime}\right) \cdot \vec{l}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} $$ $$ \varphi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \frac{\vec{p} \cdot\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} $$ • 외부 전기장 하에 놓인 전기쌍극자의 포텐셜에너지
외부전기장 $E_{\mathrm{외부}}$과 이에 대응되는 전기포텐셜 $\varphi(\vec{r})$이 주어지는 공간내에, 전기쌍극자가 놓일 때, 이 전기쌍극자의 포텐셜에너지를 구해보자. 위치 $\vec{r}$과 $\vec{r} + \vec{l}$에 놓여있는 $-q$와 $+q$의 점전하의 포텐셜에너지는 다음과 같이 주어진다. $$ U=-q \varphi_{\mathrm{외부}}(\vec{r})+q \varphi_{\mathrm{외부}}(\vec{r}+\vec{l}) $$ $\varphi_{\mathrm{외부}}(\vec{r}+\vec{l})$을 전개하면 다음과 같다. $$ \varphi_{\mathrm{외부}}(\vec{r}+\vec{l})=\varphi_{\mathrm{외부}}(\vec{r})+\vec{l} \cdot \nabla \varphi_{\mathrm{외부}}, $$ 그러면 포텐셜에너지는 다음과 같다. $$ U=q \vec{l} \cdot \nabla \varphi_{\mathrm{외부}} $$ $$ U(\vec{r})=\vec{p} \cdot \nabla \varphi_{\mathrm{외부}}, $$ $$ U(\vec{r})=-\vec{p} \cdot \vec{E}_{\mathrm{외부}}(\vec{r}) $$ 영구 쌍극자의 예

2.8 전기 다중극자

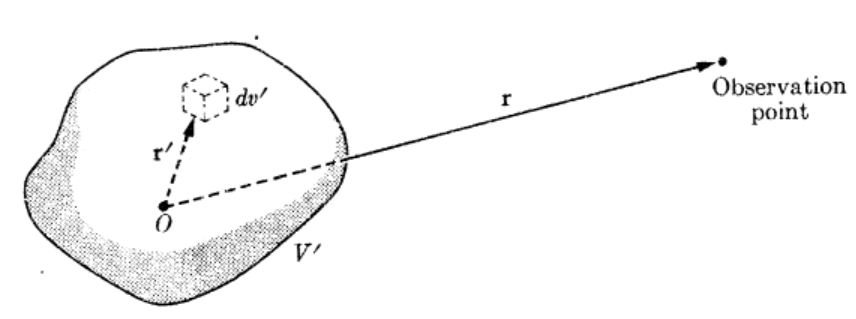
임의의 전하분포 $\rho\left(\vec{r}^{\prime}\right)$에 의한 포텐셜은 다음과 같이 주어진다. \begin{equation} \varphi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \int_V \frac{\rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d v^{\prime} \end{equation} 분모를 전개하면 $$ \begin{aligned} \left|\vec{r}-\vec{r}^{\prime}\right|^{-1} & =\left(r^2-2 \vec{r} \cdot \vec{r}^{\prime}+r^{\prime 2}\right)^{-1 / 2} \\ & =\frac{1}{r}\left(1-\frac{1}{2}\left[-\frac{2 \vec{r} \cdot \vec{r}^{\prime}}{r^2}+\frac{r^{\prime 2}}{r^2}\right]+\frac{1}{2} \frac{1}{2} \frac{3}{2}[]^2+\cdots\right) \end{aligned} $$ $$ \begin{aligned} \varphi(\vec{r})&=\frac{1}{4 \pi \epsilon_0} \int_V\left(\frac{1}{r}+\frac{\vec{r} \cdot \vec{r}^{\prime}}{r^3}+\frac{1}{2}\left[\frac{3\left(\vec{r} \cdot \vec{r}^{\prime}\right)^2}{r^5}-\frac{r^{\prime 2}}{r^3}\right]+\cdots\right) \\ &\times\rho\left(\vec{r}^{\prime}\right) d v^{\prime} \end{aligned} $$ $$ \begin{aligned} \varphi(\vec{r})= & \frac{1}{4 \pi \epsilon_0}\left(\frac{1}{r} \int_V \rho\left(\vec{r}^{\prime}\right) d v^{\prime}+\frac{\vec{r}}{r^3} \cdot \int_V \vec{r}^{\prime} \rho\left(\vec{r}^{\prime}\right) d v^{\prime}\right. \\ & \left.+\sum_{i=1}^3 \sum_{j=1}^3 \frac{1}{2} \frac{x_i x_j}{r^5} \int_V\left(3 x_i^{\prime} x_j^{\prime}-\delta_{i j} r^{\prime 2}\right) \rho\left(\vec{r}^{\prime}\right) d v^{\prime}\right), \end{aligned} $$ 위 식은 다음과 같이 표현될 수 있다. $$ \begin{aligned} \varphi(\vec{r}) = \frac{1}{4 \pi \epsilon_0} \left(\frac{q}{r} +\frac{\vec{r}}{r^3} \cdot \vec{p} +\sum_{i=1}^3 \sum_{j=1}^3 \frac{1}{2} \frac{x_i x_j}{r^5} Q_{ij}\right), \end{aligned} $$ 여기서
$q$: 전하분포를 점전하로 간주시 전하량
$\vec{p}$: 전하분포의 쌍극자 모먼트(dipole moment)
$Q_{ij}$: 전하분포의 사중극자 모먼트 텐서(quadrupole moment tensor)
$$ \vec{p}=\int_V \vec{r}^{\prime} \rho\left(\vec{r}^{\prime}\right) d v^{\prime} $$ $$ \begin{gathered} Q_{ij}=\int_V\left(3 x_i^{\prime} x_j^{\prime}-\delta_{ij} r^{\prime 2}\right) \rho\left(\vec{r}^{\prime}\right) d v^{\prime} \end{gathered} $$ 여기서 $\delta_{ij}$는 다음과 같이 주어지는 Kronecker delta 라고 한다. $$ \delta_{ij}=\left\{\begin{array}{ll} 0, & i \neq j \\ 1, & i=j \end{array}\right. $$ $\vec{p}$는 총전하가 0일 경우 원점과 무관하게 같은 값을 갖는다.
증명
$\vec{R}$을 원점으로하느 새로운 좌표계로 $\vec{p}$를 다시 표현해보면 다음을 얻는다. \begin{equation} \vec{r}^{\prime}=\vec{r}^{\prime \prime}+\vec{R} \end{equation} $$ \vec{p}=\int_V \vec{r}^{\prime} \rho\left(\vec{r}^{\prime}\right) d v^{\prime}=\int_V\left(\vec{r}^{\prime \prime}+\vec{R}\right) \rho\left(\vec{r}^{\prime}\right) d v^{\prime}=\int_V \vec{r}^{\prime \prime} \rho d v^{\prime}+\vec{R} Q $$ 총전하 $Q$가 0이면, 새로운 원점에 대한 표현은 기존 원점에 대한 표현과 같게된다.

2.9 Dirac delta 함수

식 ..에서 보는 바와 같이 전기장을 계산할 경우 전하 분포의 경우에는 적분을 라고 점전하일 경우에는 합산을 시행하였다. 만약 점전하를 다음과 같이 정의되는 Dirac delta 함수로 정의한다면 점전하에 의한 전기장 표현도 적분으로 표현할 수 있다. Dirac delta 함수는 아래와 같이 정의된다. $$ \begin{aligned} \delta(x) & = \infty & (x = 0) \\ & = 0 & (x \neq 0) \\ \end{aligned} $$ Dirac delta 함수는 다음과 같은 성질을 가진다. $$ \begin{aligned} &\int_{-\infty}^{\infty} \delta(x) d x = 1 \\ &\int_{-\infty}^{\infty} F(x)\delta(x) d x = F(0) \\ &\int_{-\infty}^{\infty} F(x)\delta(x-x_0) d x = F(x_0) \end{aligned} $$ 3차원 좌표계로 표현하면 다음과 같이 표현된다. $$ \begin{aligned} \delta(\vec{r}) & = \infty & (\vec{r} = 0) \\ & = 0 & (\vec{r} \neq 0) \\ \end{aligned} $$ $$ \begin{aligned} &\int \delta(\vec{r}) dv = 1 \\ &\int F(\vec{r})\delta(\vec{r}) dv = F(0) \\ &\int F(\vec{r})\delta(\vec{r}-\vec{r}_0) dv = F(\vec{r}_0) \end{aligned} $$ 점전하는 다음과 같이 전하분포로 표현할 수 있다. \begin{equation} \rho(\vec{r}') =q_i \delta(\vec{r}'-\vec{r}_i) \quad \text { (점전하) } \\ \end{equation} 그러면 전기 포텐셜과 전기장은 다음과 같이 표현된다. $$ \begin{aligned} \varphi(\vec{r}) & =\frac{1}{4 \pi \epsilon_0} \int \frac{q_i \delta(\vec{r}'-\vec{r}_i)}{\left|\vec{r}-\vec{r}'\right|} d v' =\frac{1}{4 \pi \epsilon_0} \frac{q_i}{\left|\vec{r}-\vec{r}_i\right|} \\ \vec{E}(\vec{r}) & =\frac{1}{4 \pi \epsilon_0} \int \frac{q_i \delta\left(\vec{r}^{\prime}-\vec{r}_i\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\left(\vec{r}-\vec{r}^{\prime}\right) d v^{\prime}=\frac{1}{4 \pi \epsilon_0} \frac{q_i}{\left|\vec{r}-\vec{r}_i\right|^3}\left(\vec{r}-\vec{r}_i\right) \end{aligned} $$ \begin{equation} \end{equation} Dirac delta 함수와 가우스 법칙을 이용하여 모든 공간에 대한 입체각이 $4\pi$가 됨을 증명할 수 있다. 가우스 법칙의 미분형은 다음과 같이 주어진다. $$ \nabla \cdot \vec{E}=\frac{1}{\epsilon_0} \rho $$ 점전하에 대응되는 값을 대입하면 다음과 같이 된다. $$ \begin{aligned} \nabla \cdot \frac{q}{4 \pi \epsilon_0} \frac{\vec{r}}{r^3} &= \frac{1}{\epsilon_0} q \delta(\vec{r}) \\ \nabla \cdot \frac{\vec{r}}{r^3} &= 4 \pi \delta(\vec{r}) \\ \nabla \frac{1}{r}=\frac{\vec{r}}{r} \frac{d}{d r}\left(\frac{1}{r}\right) &=-\frac{\vec{r}}{r^3} \\ \nabla^2\left(\frac{1}{r}\right) &=-4 \pi \delta(\vec{r}) \end{aligned} $$ $$ \begin{aligned} \nabla \cdot \frac{\vec{r}}{r^3} & =\nabla\left(\frac{1}{r^3}\right) \cdot \vec{r}+\frac{1}{r^3} \nabla \cdot \vec{r} \\ & =-\frac{3}{r^4} \frac{\vec{r}}{r} \cdot \vec{r}+\frac{3}{r^3}=0, \quad r \neq 0 \\ & =-\infty + \infty, \quad r = 0 \end{aligned} $$ $$ \int_V \nabla \cdot \frac{\vec{r}}{r^3} d v=\oint_S \frac{\vec{r} \cdot \hat{n}}{r^3} d a=\frac{1}{R^2} \oint_S d a=4 \pi $$