3. 고체의 양자이론 소개
3.1 허용된 에너지 밴드와 금지된 에너지 밴드
3.1.1 에너지 밴드의 형성
두 원자가 충분히 멀리 떨어져 있을때는 서로간의 상호작용이 미미하나,
점점 서로 접근함에 따라 서로 상호작용 및 교란이 발생하여
각 원자의 전자들은 원래의 에너지에서 미세한 변화를 경험한다(그림 3.1(a,b)).
그림 3.1(c)은 이러한 두 원자들의 전자들이 격는 미세한 에너지 분리현상을 보여준다.
이것은 고체에서 에너지 밴드가 형성되는 원리가 된다.
Pauli의 배타원리에 의하여, 각 에너지 상태에는 전자가 1개씩만 존재할 수 있다.
이로 인하여 두 전자는 분리된 두 에너지에 각각 하나씩만 존재하게 된다.
다르게 표현하면 분리된 두 에너지가 $E_1$, $E_2$라면
두 전자는 각각 $E_1$, $E_2$의 에너지를 갖게 된다.
두 전자가 동일하게 $E_1$을 갖거나 $E_2$를 가질 수는 없다.
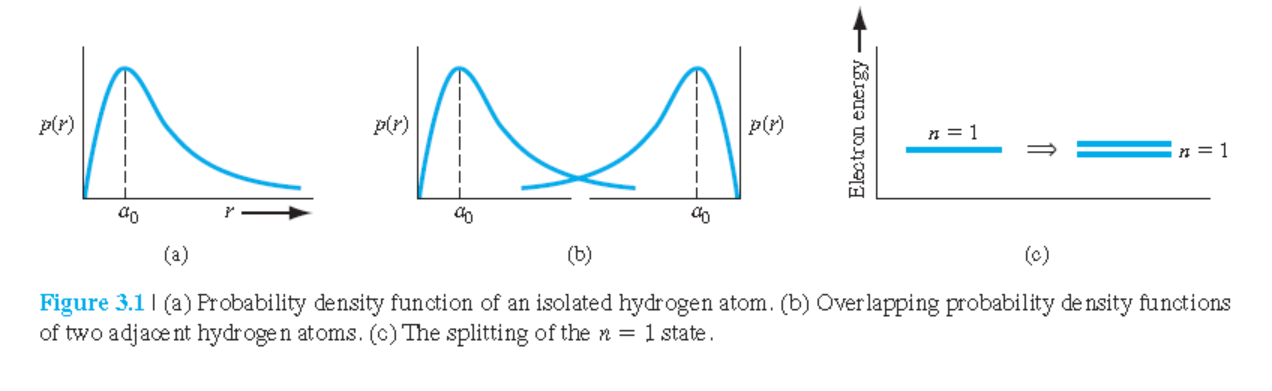
그림 3.2 설명: 원자간 간격이 감소할수록 에너지분리(splitting) 현상이 확대된다.
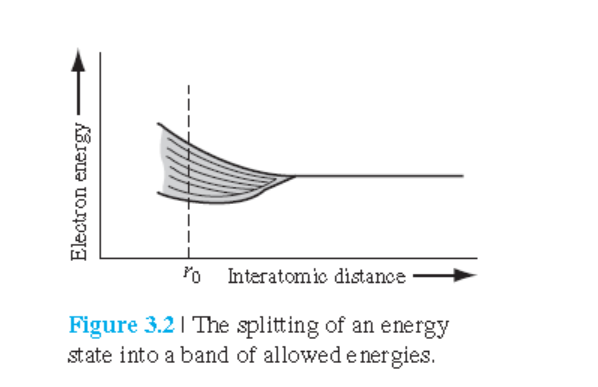
$r_0$ : 원자들이 서로 접근하면서 결정을 이룰 때의 평형 거리
단일 원자와는 달리 실제 고체 물질에서는 엄청난 수의 전자를 가지고 있다.
$10^{19}$개의 전자들로 구성된 시스템을 가정하자.
이 경우에도 에너지 분리 현상은 동일하게 발생하여 미세한 간격으로 분리된 에너지들은 하나의 밴드를 형성한다.
분리된 에너지들의 간격은 다음과 같이 유추가 가능하다.
원자간 평형간격이 형성되었을때,
에너지 밴드의 폭이 1eV, 밴드내의 에너지간격이 등간격이라고 가정하면,
밴드내의 에너지 값들은 $10^{-19}$ eV 간격으로 떨어져 있어야 한다.
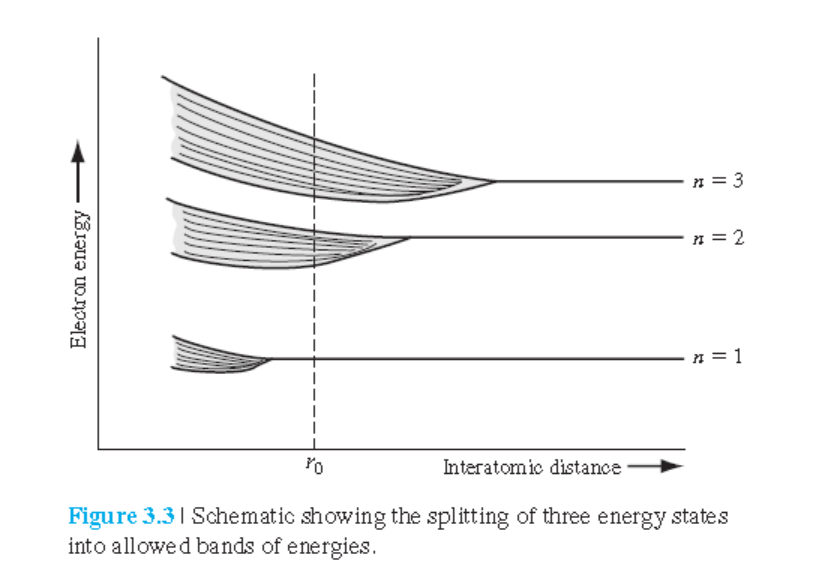그림 3.3: 원자간 거리가 감소할수록 각 양자수 레벨에너지 분리의 확대. 허용 밴드(allowed band), 금지 밴드(forbidden band)
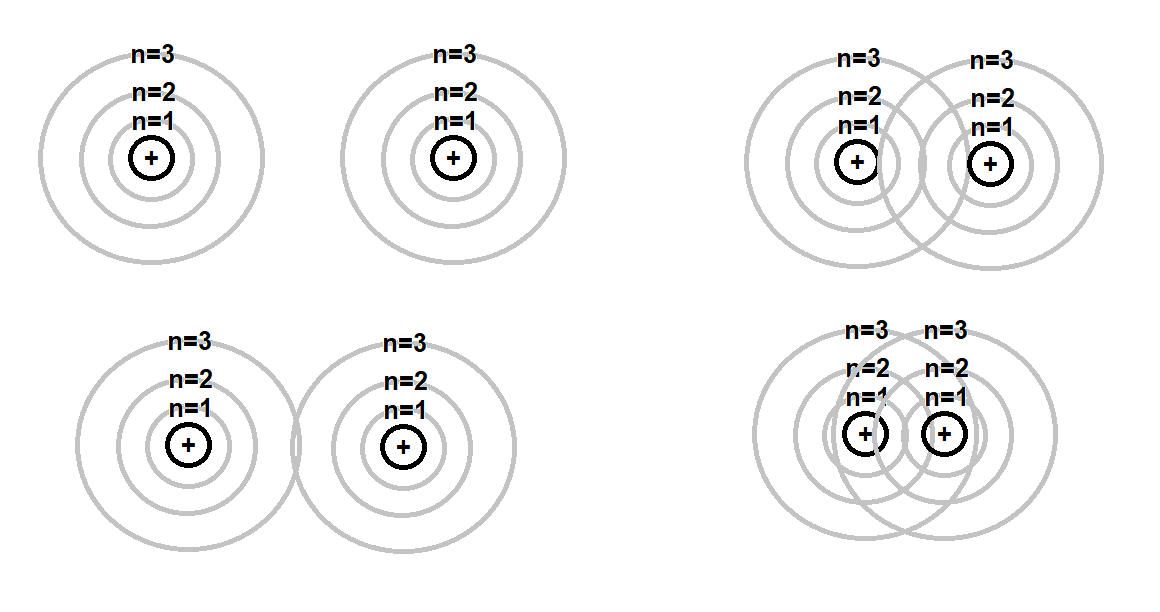
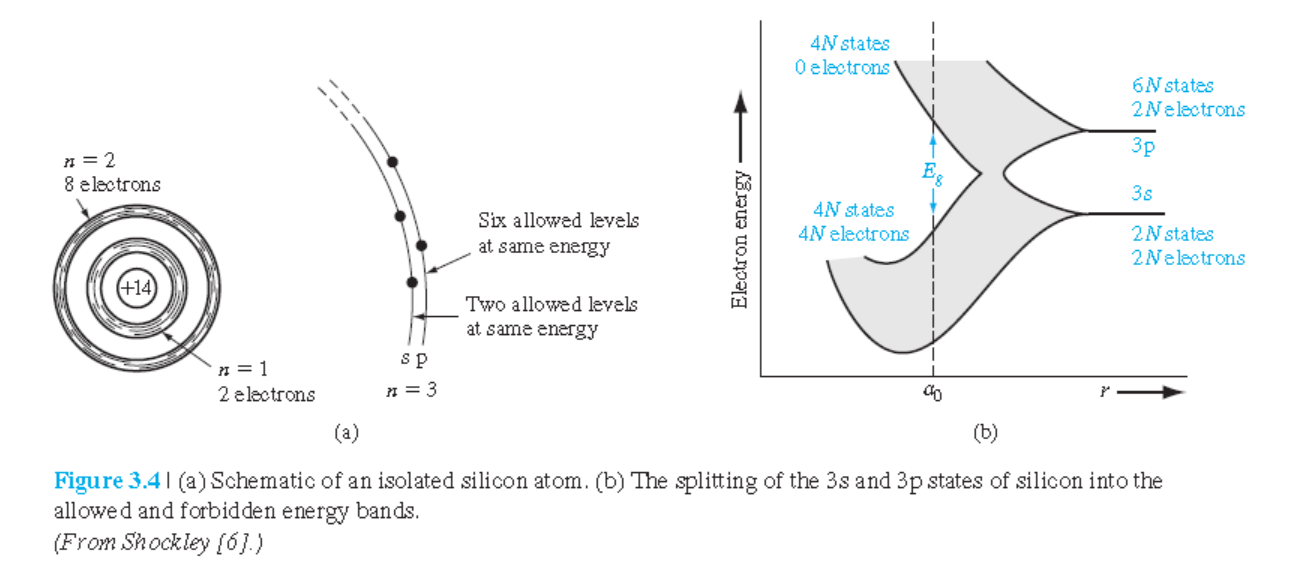
그림 3.4 : Si원자의 경우 원자간 거리감소에 따른 에너지 분리현상
실제 결정에서의 밴드 분리는 그림 3.3보다 훨씬 복잡하다.
Si원자의 경우 전자 14개중에서 10개는 원자핵에 가까운 에너지 준위를 차지하고 나머지 4 개의 전자는 외곽에 존재하는데
$2s^2p^2$의 궤도를 차지하게 된다.
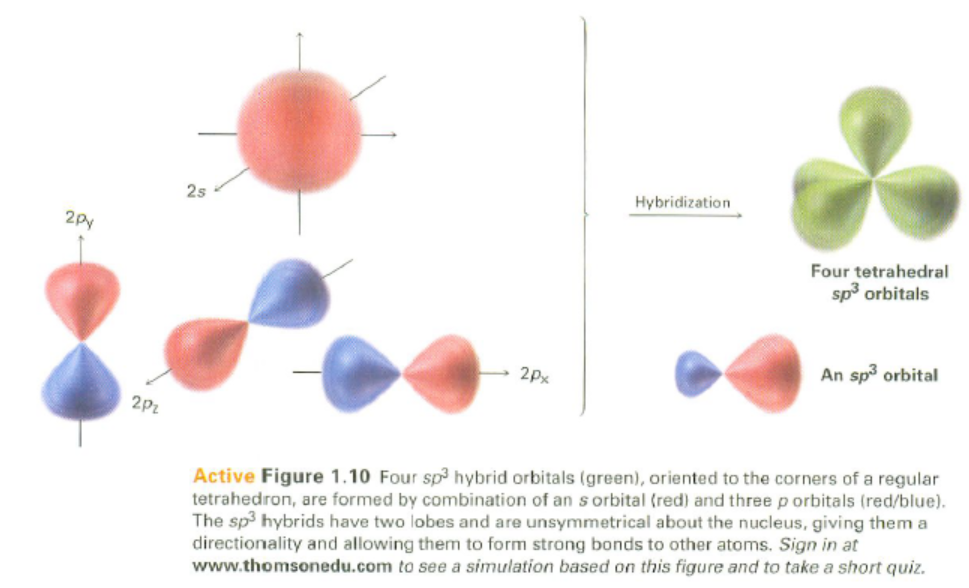
그러나 Si원자가 결정을 이루게 되는 경우 Si원자들이 서로 가까워지면서 외곽전자들이 교란을 일으키게 되고
외곽의 4개의 전자들이 차지하는 괘도는 $2s^2p^2$에서 $sp^3$혼성궤도로 바뀌게된다.
전자가 상대적으로 풍부한 낮은 에너지 밴드를 가전자대(valence band) ,
전자가 상대적으로 희박한 높은 에너지 밴드를 전도대(conduction band),
그리고 전도대와 가전자대 사이의 간격을 에너지갭($E_g$)이라고 부른다.
3.1.2 Kronig–Penney 모델
Bloch 정리
$$\Psi(x) = u(x) e^{ikx} \quad\quad\quad(3.1)$$
$u(x)$ : 주기함수, $\hbar k$: crystal momentum(결정운동량)
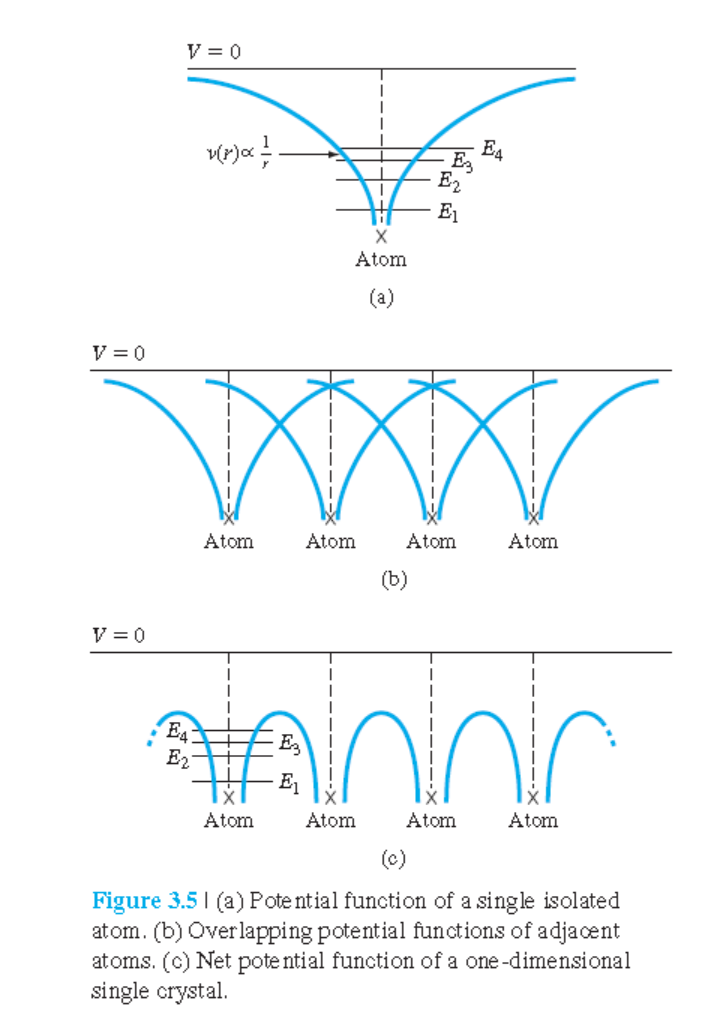
경계조건등을 적용하여 다음과 같은 결론을 얻는다.
$$
P' \frac{\sin \alpha a}{\alpha a}+\cos \alpha a=\cos k a \qquad (3.24)
$$
여기서 $P'$과 $\alpha$는 다음과 같이 주어진다.
$$
P'=\frac{m V_0 b a}{\hbar^2}, \quad \alpha = \sqrt{\frac{2mE}{\hbar^2}}
$$
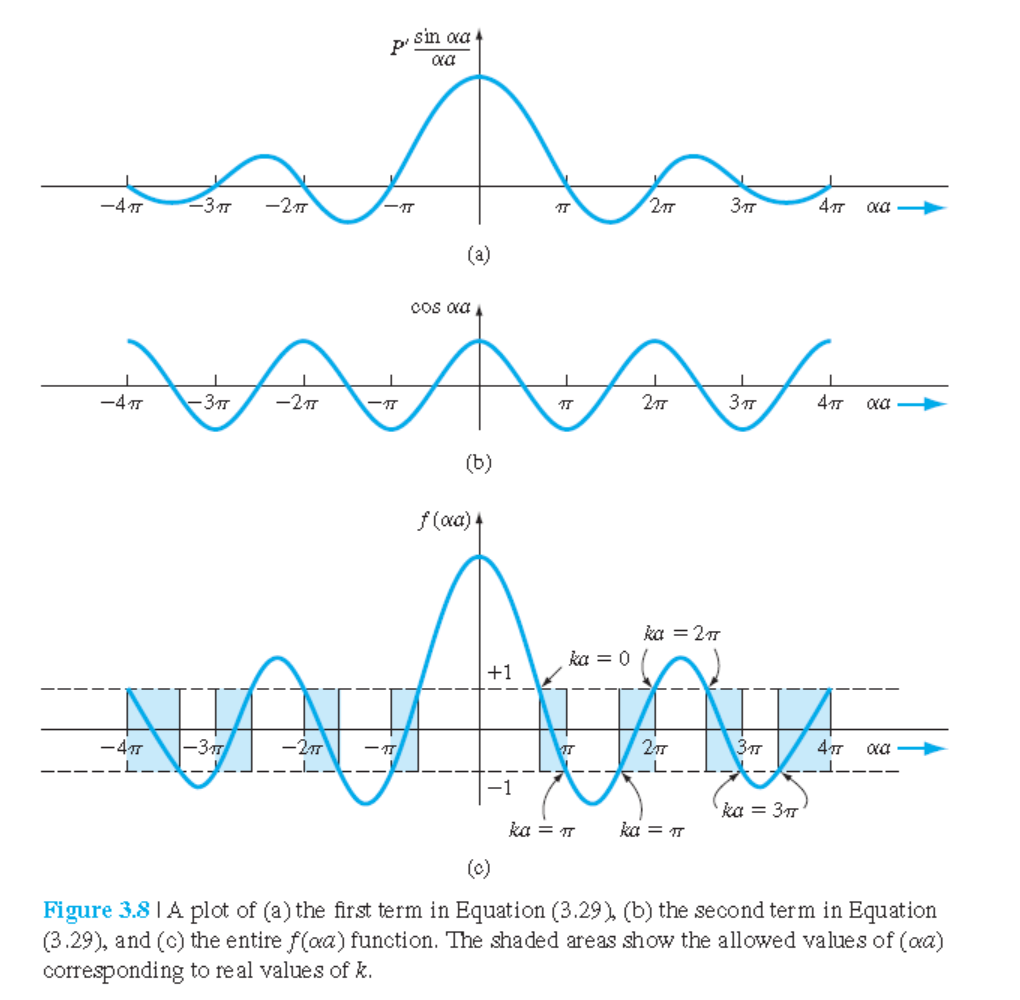
$ -1 < \cos k a < 1 $ 라는 것을 고려하면, 식 (3.24)가 가질 수 있는 해는 제한된다.
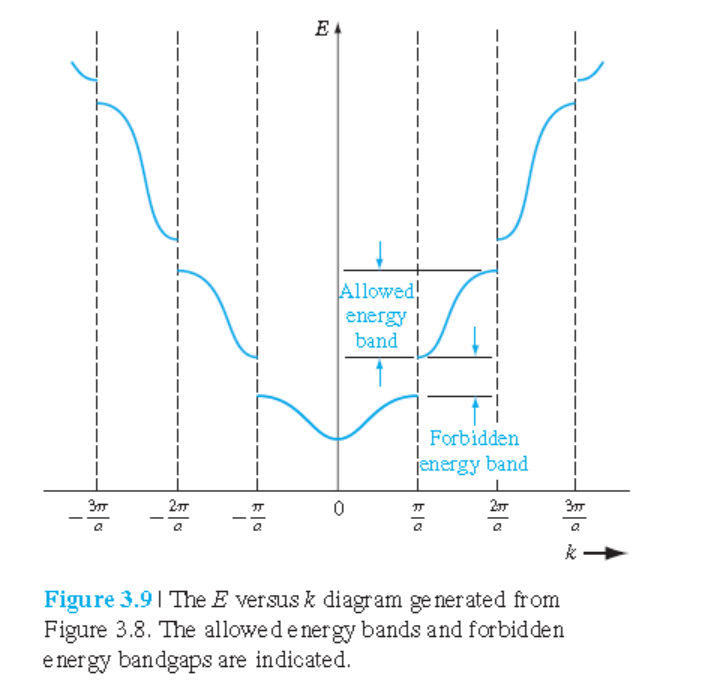
3.1.3 The k -Space Diagram
Kronig–Penney 모델의 해를 $E$-$k$ Diagram으로 그리면 아래와 같다.
자유전자와 비교
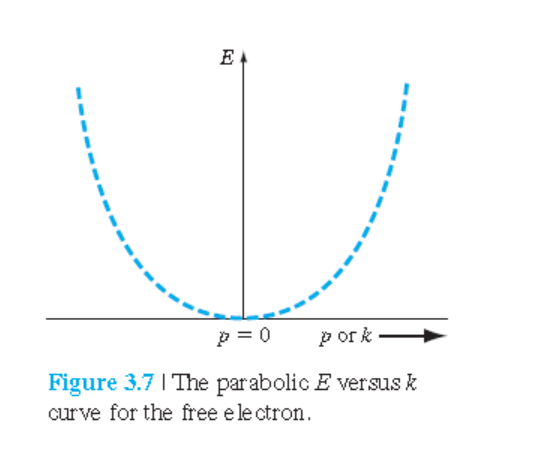
자유전자 : $p=\hbar k$
$$ E=\frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m} \quad\quad\quad (3.28)$$
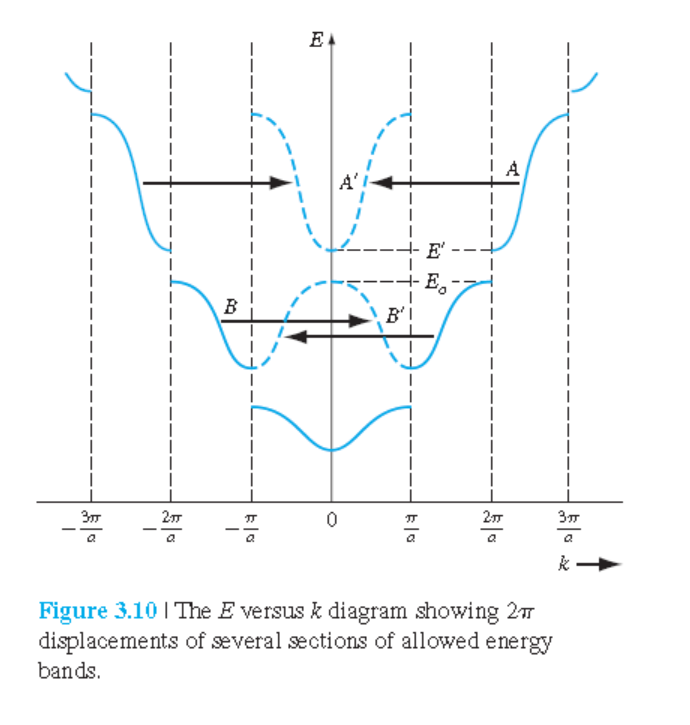
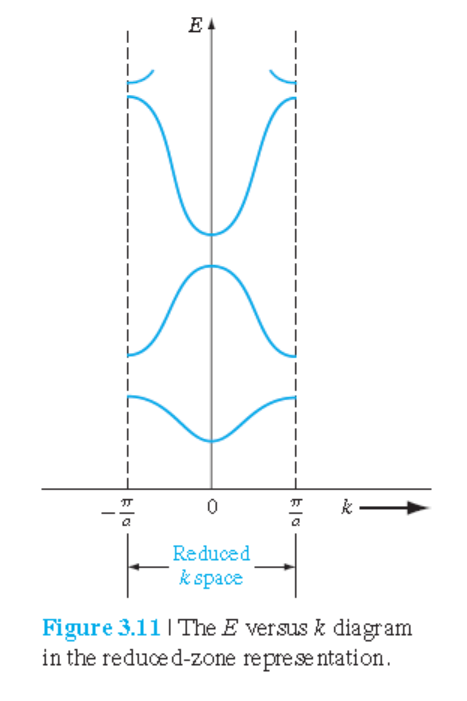그림 3.11 처럼 그려진 형태를 reduced zone scheme이라고 하며,
그 reduced zone을 첫번째 brillouin zone이라고 한다.
3.2 고체에서 전자 전도
3.2.1 에너지 밴드와 결합 모델
온도 $= 0$ K 일때
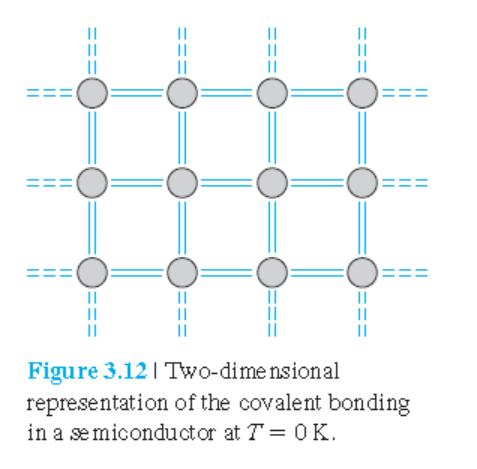
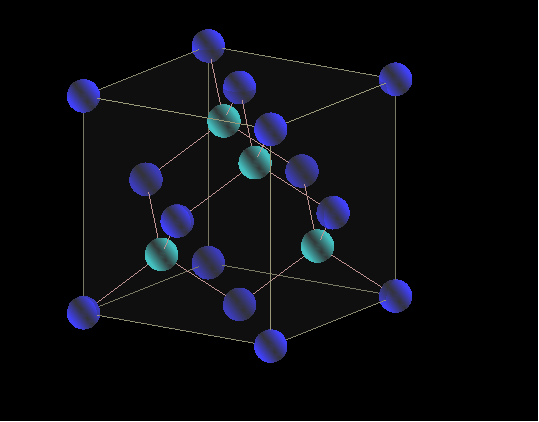
온도가 0 K일 때, 각 Si원자들은 8개의 가전자들에 둘러싸여 있고, 공유결합에 직접관여한다.
그림 3.4(b)에 보이는 valence(가전자) 밴드에 그 전자들이 존재하며, conduction(전도) 밴드에는 전자가 존재하지 않는다.
온도 $> 0$ K 일때
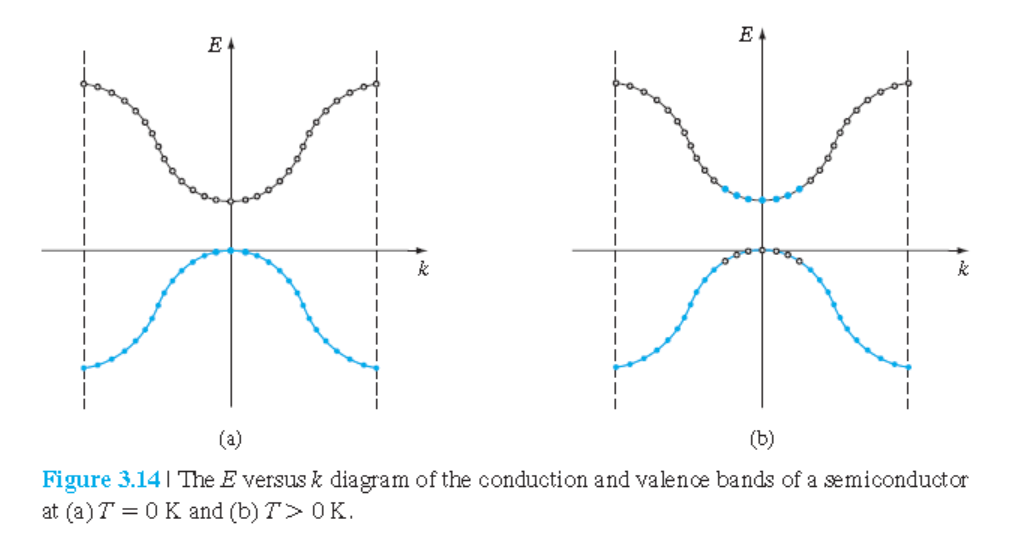
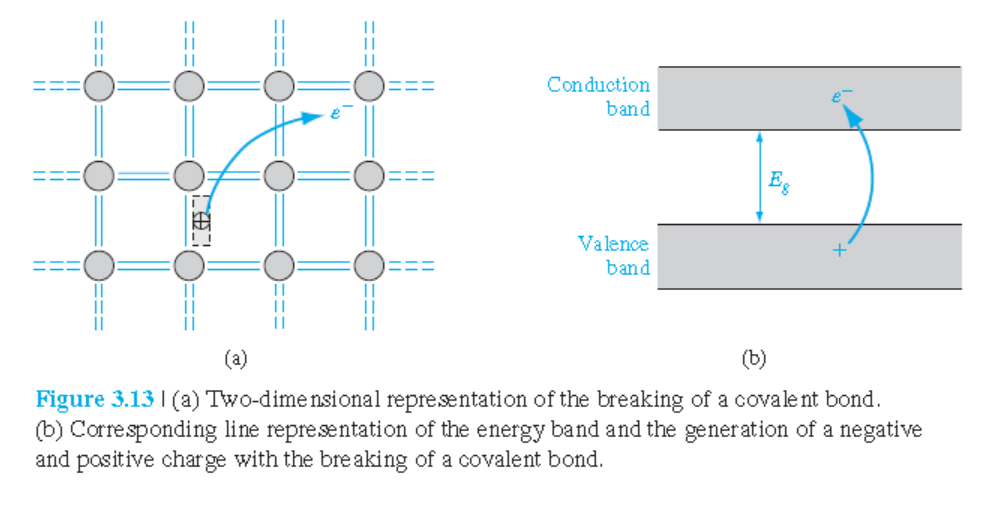온도가 $0 K$위로 약간 올라가면, 가전자들의 일부는 에너지를 얻어서, 그림 3.13(a)처럼 공유결합을 깨고 더 높은 에너지 상태가 된다.
에너지적으로는 전자가 valence 밴드에서 conduction 밴드로 이동한다.
온도가 더 증가하면 더 많은 전자들이 valence 밴드에서 conduction 밴드 이동한다.
(주의할 것은 전자가 valence 밴드에서 conduction 밴드 '이동'한다는 표현은
전자의 에너지가 증가한다는 것이지 반드시 공간적으로 어딘가로 이동한다는 것을 의미하지는 않는다. )
이와 같은 거동은 $E$-$k$ 곡선에서 다음 그림과 같이 나타난다.
3.2.2 Drift Current(표류 전류)
전기장에 의한 전하의 흐름을 drift라고, 이 전류를 drift 전류라고 한다.
부피밀도 N(cm$^{-3}$)이고 전하 q를 가진 전하들이 평균 drift 속력 $v_d$를 가질때 전류밀도는 다음과 같이 주어진다.
$$J=Nqv_d (\mathrm{A/cm}^2) \quad\quad\quad (3.32)$$
전하를 운반하는 carrier(운반자)는 전자와 hole 이 두가지가 있으며, 전자에 의한 drift 전류를 논의해 보자.
conduction 밴드에 있는 전자에 의한 drift 전류는 다음과 같이 쓸수있다.
$$J_n = -e \sum_{i=1}^N v_i \quad\quad\quad (3.35) $$
$N$은 conduction 밴드에서 단위부피당 전자수이다.
이 식을 그림 3.14에 적용하면 전류는 0이 될것이다.
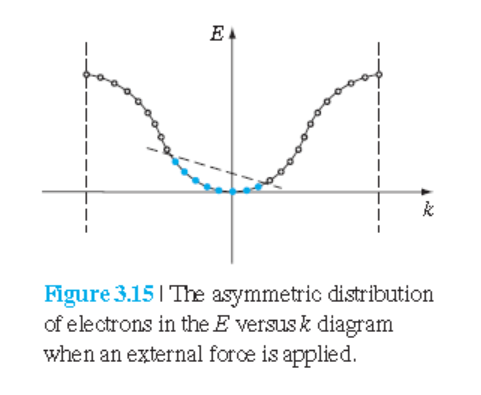
만약 전기장이 가해져서 아래와 같은 에너지 변화를 격는다면
$$dE = Fdx = Fvdt \quad\quad\quad (3.34) $$
그림 3.15처럼 되어 전류가 발생할 것이다.
3.2.3 Electron effective mass(전자 유효질량)
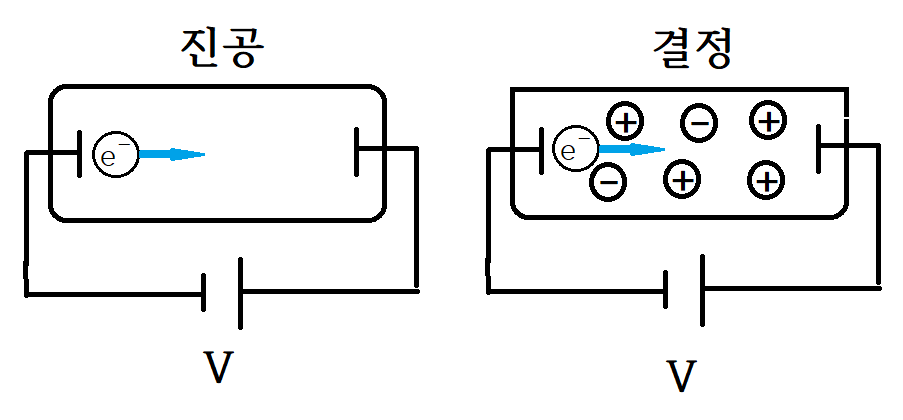
전기장을 가했을때 전자가 가속하는 것은 마찬가지지만
진공에서와 결정내에서의 가속도는 다를 것이다.
결정내에서는 전자의 가속도에 영향을 미치는 다양한 내부 요소들이 있다.
그래서 결정내의 전자의 운동을 제대로 기술하는 것은 쉽지 않은 일이다.
그러나 질량이 원래 질량과는 다른 어떤 특정 값이라고 가정하게 되면,
결정내의 전자의 거동을 마치 진공에서의 거동과 동일하게(가속도가 같다고) 취급할 수 있다.
이렇게 하면 결정내의 전자를 기술할때 복잡한 내부 요소들을 제거할 수 있어서,
결정내의 전자를 기술하는 것이 용이하게 된다.
$$ F_{\mathrm{total}} = F_{\mathrm{ext}} + F_{\mathrm{int}} = ma \quad\quad\quad (3.36)$$
$F_{\mathrm{total}}$ : 전체 힘
$F_{\mathrm{ext}}$ : 외부힘(양쪽 전극)
$F_{\mathrm{int}}$ : 내부힘
$$ F_{\mathrm{ext}} = m^*a \quad\quad\quad (3.37)$$
$m^*$: effective mass(유효질량)
위와 같이 유효질량을 도입하면 결정내의 전자의 운동은
마치 (유효질량을 가진) 전자가 진공속에서 양쪽전극(외부힘)에 의해 가속되는 것처럼 기술할 수 있다.
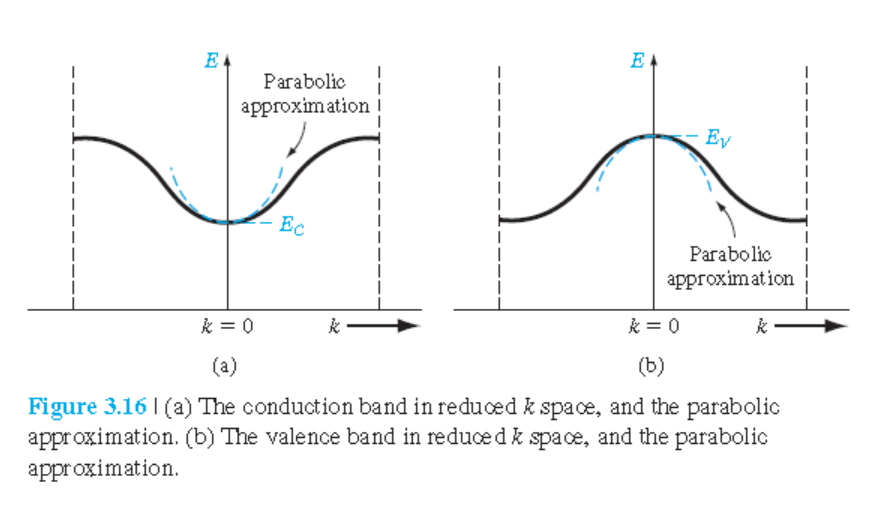
• $E$-$k$ 곡선에서 유효질량 구하기
자유전자의 에너지와 질량의 관계
$$E=\frac{1}{2}mv^2 = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m} $$
($p=\hbar k$는 자유전자에서 성립)
양변을 $k$로 미분하면
$$\frac{dE}{dk} = \frac{\hbar^2 k}{m} \quad\quad\quad(3.38)$$
참고로 속도와 $E$-$k$곡선의 기울기는 다음의 관계가 있다.
$$v = \frac{p}{m} = \frac{\hbar k}{m} = \frac{1}{\hbar}\frac{dE}{dk} \quad\quad\quad(3.39)$$
(3.38)식을 한번 더 미분하면
$$\frac{d^2E}{dk^2} = \frac{\hbar^2}{m} $$
$$ \frac{1}{m} = \frac{1}{\hbar^2} \frac{d^2E}{dk^2} \quad\quad\quad (3.41)$$
이 식을 $E$-$k$ 곡선에 적용하면 유효질량($m^*$)를 구할 수 있다.
$$ \frac{1}{m^*} = \frac{1}{\hbar^2} \frac{d^2E}{dk^2} $$
전자가 conduction 밴드에 있다면, $m^*>0$이다.
conduction 밴드 하단에 있는 전자에 전기장 $\mathcal{E}$를 가하면 가속도는 다음과 같이 주어진다.
$$F= m^*a = -e \mathcal{E}$$
$$a = -\frac{e \mathcal{E}}{m^*} \quad\quad\quad(3.48)$$
(참고로 엄밀하게는 유효질량는 밴드 최저점에서만 적용되는 근사로서 생각해야한다.)
3.2.4 Hole의 개념
그림 3.13에서 처럼 온도가 0 K이상으로 올라가면, 에너지를 얻은 전자는 공유결합을 깨고,
더 높은 에너지 상태로 올라간다.
이 과정에서 전자가 비게된 원자는 양전하를 띄게된다.
이 양전하는 다른 원자에서 탈출한 전자에 의해 채워지며, 양전하가 되는 원자는 바뀌게된다.
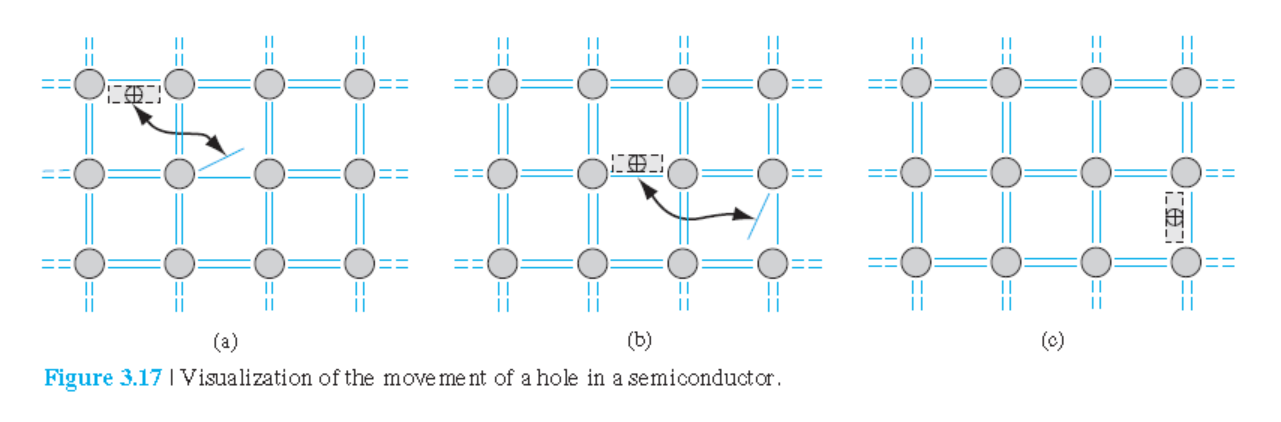
그림 3.17은 이러한 과정을 보여 주며, 전자가 비게되어 양전하를 띈 어떤 가상의 입자가 마치 이동하는 듯한 현상을 보여주는 데,
이것은 양전하의 흐름(=전류)과 동일하게 간주될 수 있다.
이 전류를 일으키는 양전하 carrier를 hole이라고 한다.
valence 밴드에 있는 hole들에 의한 drift 전류는 다음과 같이 주어진다.
$$J_h = -e \sum_{i(\mathrm{채워진})} v_i = -e \left[ \sum_{i(\mathrm{전체})} v_i - \sum_{i(\mathrm{비워진})} v_i\right] \quad\quad\quad (3.49) (3.50)$$
$\sum_{i(\mathrm{전체})} v_i = 0 $ 이므로 다음이 성립한다.
$$J_h = + e \sum_{i(\mathrm{비워진})} v_i \quad\quad\quad (3.52)$$
여기서 $v_i$는 식 (3.39)로 주어지는 속도를 가진다.
$$v_i(E) = \frac{1}{\hbar} \left( \frac{dE}{dk}\right) \quad\quad\quad (3.39)$$
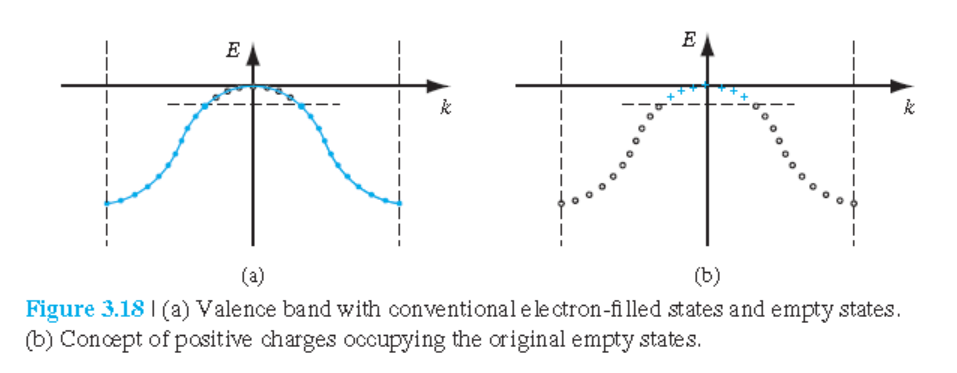
전기장 $\mathcal{E}$를 결정에 가하면 valence 밴드 상단에 있는 전자들의 가속도는 다음과 같이 주어진다.
$$F= m^*a = -e \mathcal{E} \quad\quad\quad (3.57)$$
여기서 $m^* < 0 $
$$a = \frac{- e \mathcal{E}}{-\left| m^* \right|} = \frac{e \mathcal{E}}{\left| m^* \right|} \quad\quad\quad (3.58)$$
에너지밴드 상단에 있는 전자는 가해지는 외부전기장과 같은 방향으로 가속됨을 의미한다.
이 또한 hole의 전하가 양이라는 것을 말해준다.
3.2.5 절연체, 반도체, 금속
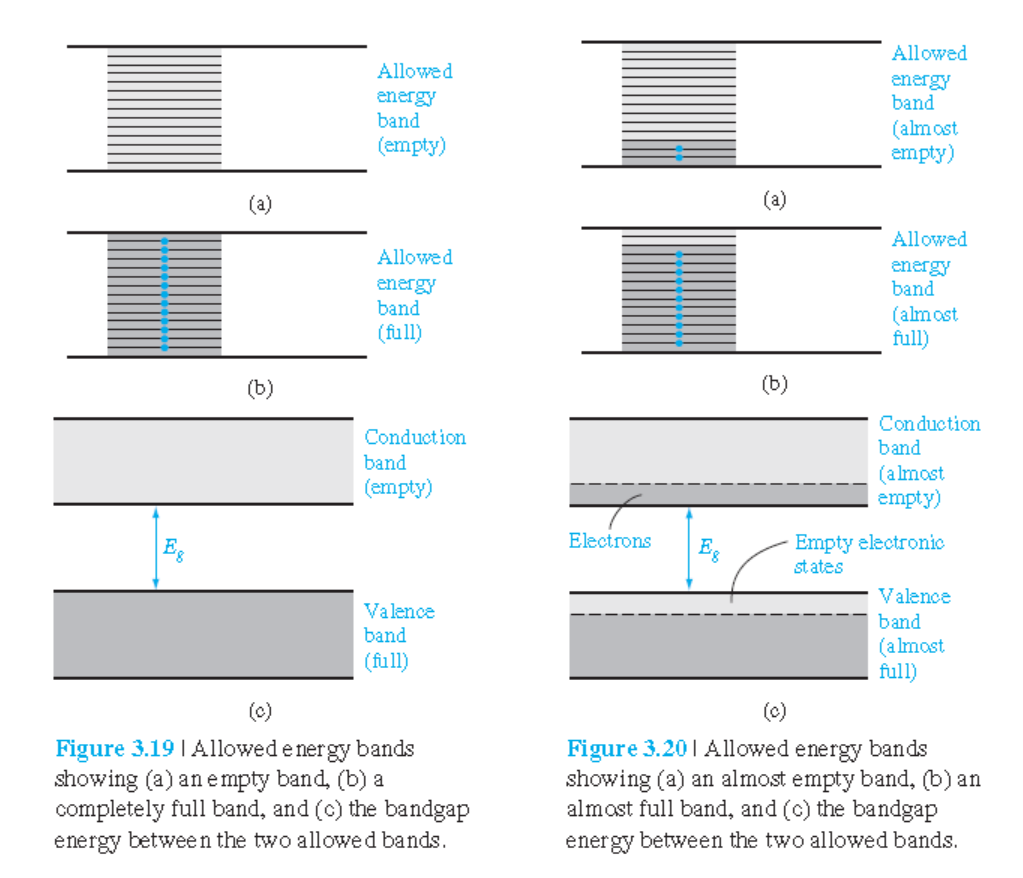
• Insulator(절연체) (그림 3.19(a))
° $T=0$ K에서 뿐만이 아니라 상온에서도 conduction 밴드는 완전히 비어있고, valence 밴드는 완전히 채워져 있음.
° 전기장을 가해도 전류가 거의 0 임.
° resistivity(비저항)이 매우 큼. 또는 (conductivity)전도도가 매우 작음.
° bandgap : 3.5 ~ 6 eV
• Semiconductor(반도체) (그림 3.20)
° $T=0$ K에서는 conduction 밴드는 완전히 비어있고, valence 밴드는 완전히 채워져 있음.
° 온도가 올라가면서 valence 밴드에 있는 전자의 일부가 conduction 밴드로 올라감.
° bandgap : 1.0 eV
° 전기장을 가하면 전류 발생.
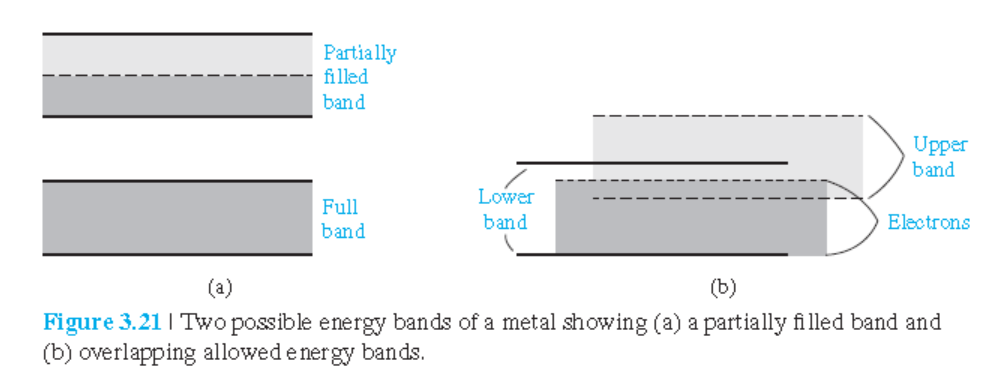
• Metal(금속) (그림 3.21(a))
° $T=0$ K에서 valence 밴드는 완전히 채워져 있고, conduction 밴드는 일부가 채워져 있음.
° 전기장을 가하면 전류 발생.
° 낮은 resistivity 또는 높은 conductivity.
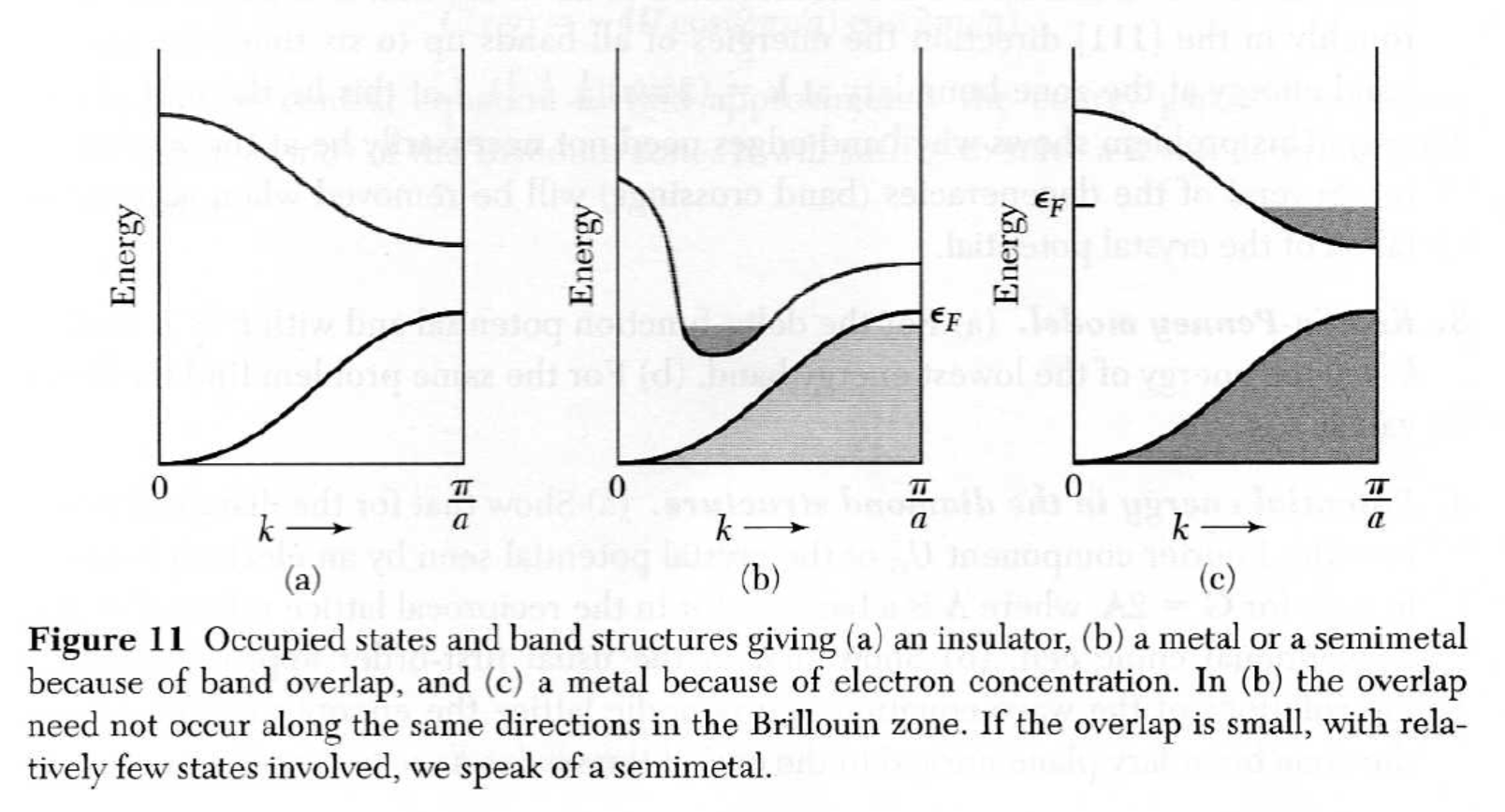
• Semimetal(금속) 또는 metal (그림 3.21(b))
° valence 밴드와 conduction 밴드가 부분적으로 겹칩.
° $T=0$ K에서 valence 밴드의 상단이 비어있고, conduction 밴드의 하단이 채워져 있음.
° 전기장을 가하면 전류 발생.
° 낮은 resistivity 또는 높은 conductivity.
3.3 3차원으로 확장
이제까지 전자의 한 방향에 대해 $E$-$k$ 곡선(허용 밴드, 금지 밴드, 유효질량)을 얻었다.
그러나 결정은 3차원이기 때문에 다양한 방향으로의 $E$-$k$ 곡선 정보가 종종 필요하다.
방향에 따라 원자 성분, 원자간격등이 달라진다.
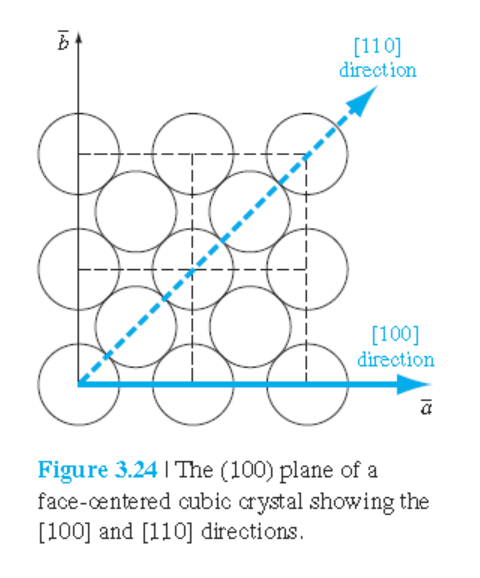
그림 3.24에서 보는 바와 같이 FCC 결정에서 [100]방향과 [110]방향으로의 원자구성이 달라짐을 확인할 수 있다.
3.3.1 Si와 GaAs의 $E$-$k$ diagram
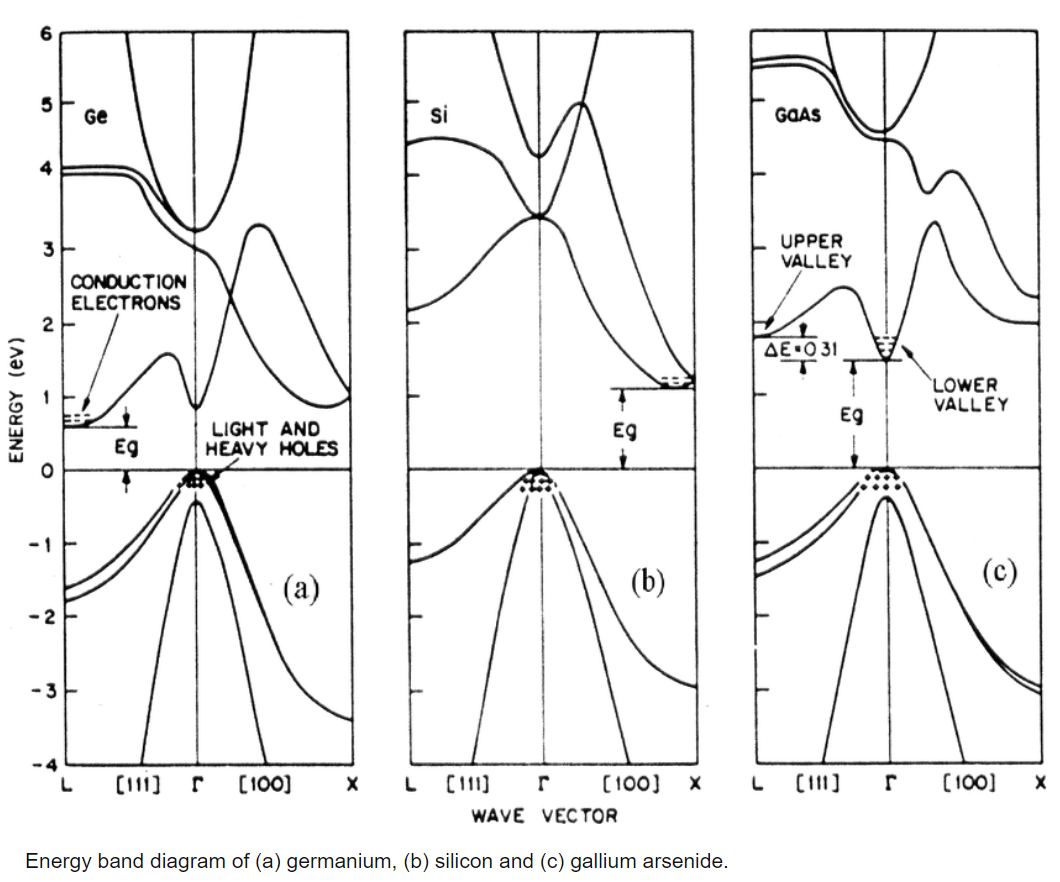
그림 3.25는 GaAs와 Si에 대한 $E$-$k$ 에너지 밴드를 보여준다.
[100]방향을 $+k$축에 [111]방향을 $-k$축에 두는 것이 일반적이다.
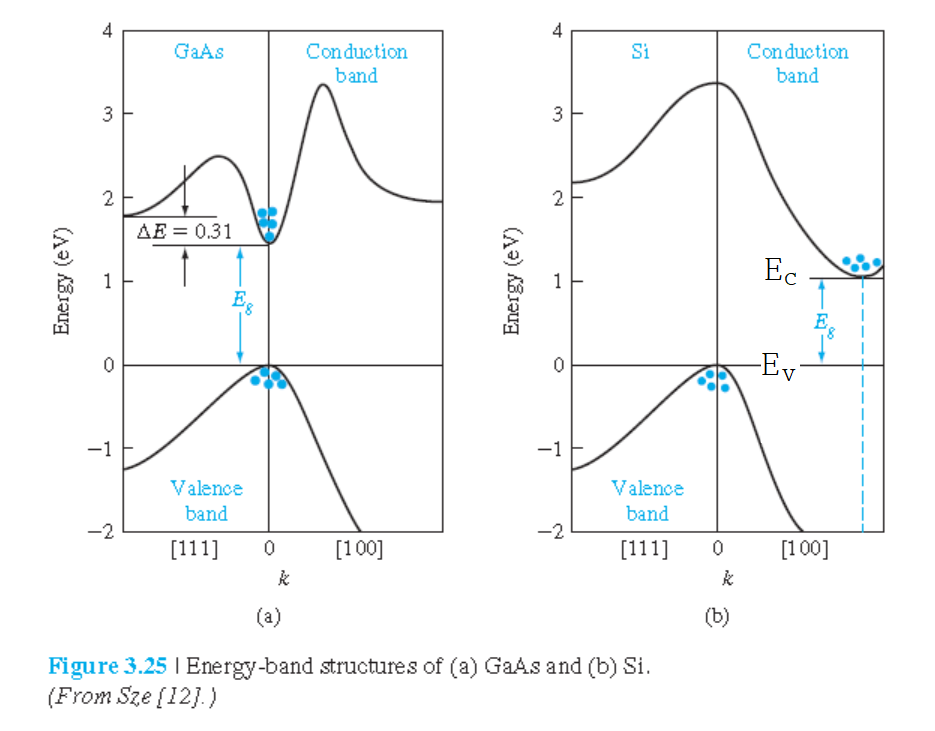
그림 3.25(a)는 GaAs의 $E$-$k$ 곡선을 보여준다.
valence 밴드의 최대점과 conduction 밴드의 최소점은 같은 $k$값을 가진다.
이러한 반도체를 direct gap 반도체라고 한다.
이 반도체에서 밴드간 전이를 할때는 운동량변화가 일어나지 않는다.
direct gap 반도체들은 레이저, 광소자등에 사용하기에 적합하다.
그림 3.25(b)는 Si의 $E$-$k$ 곡선을 보여준다.
valence 밴드의 최대점은 conduction 밴드의 최소점은 같은 $k$값이 아니다.
valence 밴드의 최대점은 $k=0$에 일치하지만,
conduction 밴드의 최소점은 [100]방향에서 존재한다.
valence 밴드의 최대점과 conduction 밴드의 최소점사이의 에너지 간격을 band gap이라고 한다.
이러한 반도체를 indirect gap 반도체라고 한다.
band간 전이시 운동량 보존을 만족시켜야하는데, 이것은 전자-포논 상호작용으로 이루어진다.
• Direct gap반도체와 indirect gap반도체에서의 흡수
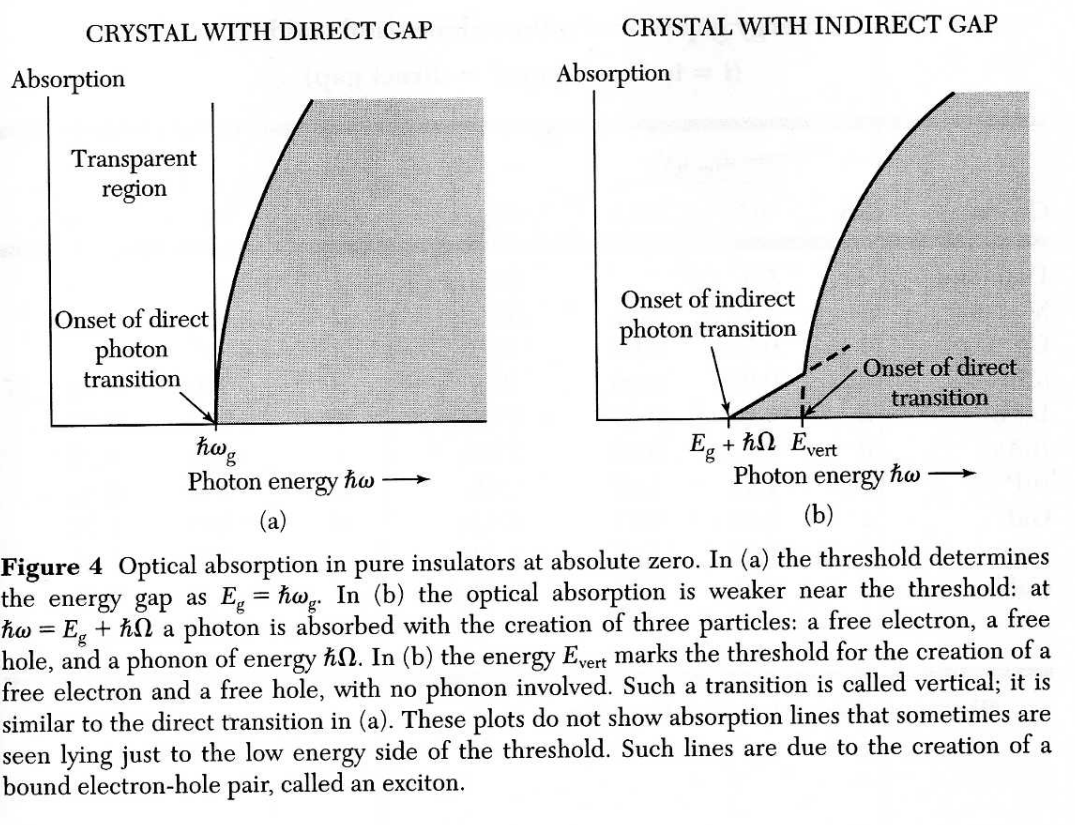
• Ge의 $E$-$k$ band.
GaP, AlAs : indirect gap semiconductor
3.3.2 유효질량의 추가적인 개념
그림 3.25로부터 GaAs의 유효질량가 Si의 것보다 더 작은 것을 알수있다.
$$\frac{1}{m^*}=\frac{1}{\hbar}\frac{d^2E}{dk^2}$$
유효질량이 작을 수록 빨리 반응(고속소자에 적합).
실제 3차원 결정에서는 $k$는 3가지 값을 가질 수 있으므로,
유효질량도 3가지 값을 가질 수 있다.
3.4 상태 밀도 함수(denssity of states function)
• 이 과목의 목표: 반도체 소자의 전류-전압 특성.
전도에 기여하는 carrier들(전자와 hole)의 수를 결정하는것이 중요한데,
이것을 하기위해서 상태 밀도(density of state, 양자상태수/(cm$^3$ eV))를 이해 할 필요가 있다.
• 상태 밀도
: 단위 에너지당 단위 부피당 상태수
: 특정 에너지 주위의 미미한 에너지 간격내에 state가 얼마나 들어있는 지 알려줌.
3.4.1 수학적 유도
상태 밀도를 에너지 함수로 결절하기 위해 적절한 모델을 설정하자.
반도체의 conduction 밴드에서 전자들은 비교적 자유롭게 이동할 수 있지만,
결정내부에 갖혀있다.
좀더 구체적으로 한변의 길이가 $a$인 정육면체 형태의 반도체내에 자유전자들이 갖혀있는 것으로 볼수있다.
이러한 상황은 자유전자들이 다음과 같은 무한 포텐셜우물에 갖힌 것으로 단순화될 수 있다.
$$V(x,y,z)=0 \quad \mathrm{for}\quad\quad 0 < x < a, 0 < y < a, 0 < z < a \quad (3.59) $$
$$V(x,y,z)=\infty \quad\quad \mathrm{elsewhere} $$
위 포텐셜에 대한 Schrodinger방정식의 해는 2.3.2절에서 했던 1차원 무한 포텐셜우물을 참고하여 얻어질 수 있다.
에너지는 다음과 같이 주어진다.
$$\frac{2mE}{\hbar^2} = k^2 = k_x^2 + k_y^2 + k_z^2 = (n_x^2 + n_y^2 + n_z^2)\left( \frac{\pi^2}{a^2}\right) \quad (3.60)$$
여기서 $n_x$, $n_y$, $n_z$은 양의 정수들이다.
그림 3.26에 허용된 양자상태를 표현한 그림이 있다. 양의 $k$ 값만 표현되어 있다.
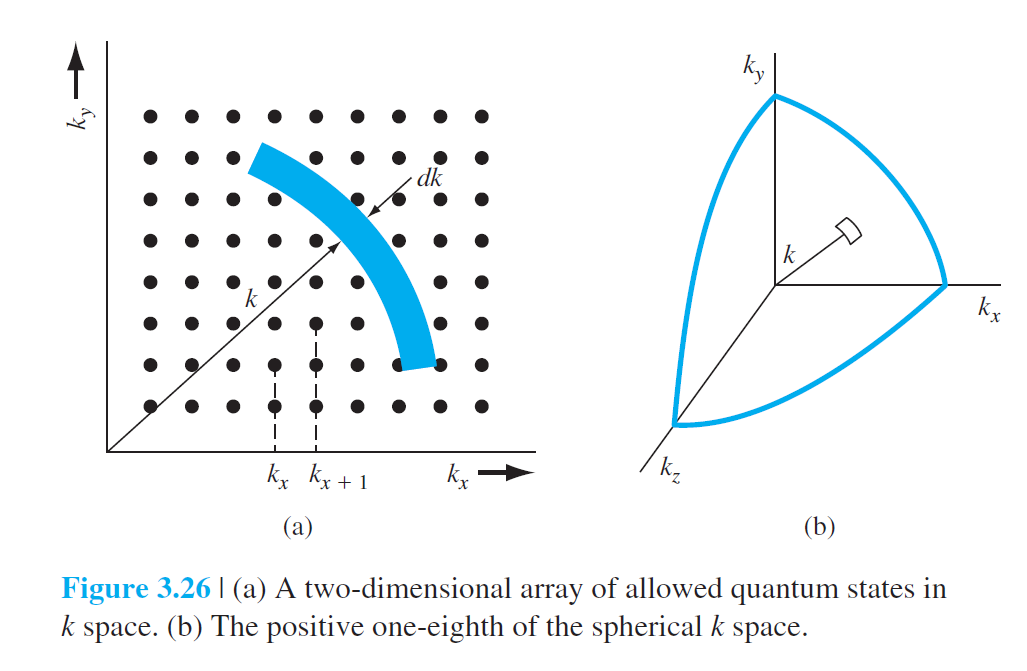두 이웃한 $k$ 점 사이의 간격을 구해보자.
$$ k_{x+1} - k_x = (n_x+1)\frac{\pi}{a}-n_x\frac{\pi}{a}=\frac{\pi}{a} \quad (3.61)$$
그러면 3차원 $k$공간에서 $k$점 하나에 대응되는 부피는 다음과 같이 주어진다.
$$\left(\frac{\pi}{a} \right)^3 \quad (3.62)$$
에제 상태 밀도룰 구해보자.
원점에서 $k$만큼 떨어진 반경 $k$인 구 껍질을 생각하자. 구 껍질의 두깨는 $dk$이다.
그러면 구 껍질의 부피는 다음과 같이 주어진다.
$$ \frac{1}{8} (4\pi k^2) dk$$
위 식을 (3.62)식으로 나눠주면 구껍질내에 존재하는 $k$점들의 수가 된다.
스핀까지 고려하면 반경 $k$인 구 껍질에 존재하는 양자상태수는 다음과 같이 된다.
$$ g(k)dk = 2\frac{1}{8} \frac{4 \pi k^2 dk}{\left(\frac{\pi}{a} \right)^3} \quad (3.63)$$
위에서 $g(k)$은 상태밀도이다. 위 식을 정리하면
$$ g(k)dk = \frac{a^3}{\pi^2}k^2 dk $$
$k$로 표현되어 있는 위 식을 다음 자유전자의 식을 이용하여 에너지 $E$로 표시해보자.
$$ k^2 = \frac{2mE}{\hbar} \rightarrow dk = \frac{1}{\hbar}\sqrt{\frac{m}{3E}}dE $$
위 식을 이용하면 정리하면
$$ g(E) = \frac{4\pi(2m)^{3/2}}{h^3} \sqrt{E} \quad (3.69)$$
3.4.2 반도체로의 확장
• Conduction 밴드 하단에 있는 전자의 상태 밀도
앞 절에서 일반적인 모델에서 유도한 상태 밀도를 conduction 밴드와 valence 밴드가 있는 상황에서 구해본다.
자유전자에서 에너지와 $k$의 관계는 다음과 같이 얻어진다.
$$ E= \frac{\hbar^2 k^2}{2m}$$
conduction 밴드하단에 대해서 $E$-$k$ diagram을 다음과 같이 표현할 수 있다.
$$ E= E_c + \frac{\hbar^2 k^2}{2m_n^*} \quad\quad\quad (3.70)$$
$m_n^*$: 전자의 유효질량.
$$\rightarrow E-E_c= \frac{\hbar^2 k^2}{2m_n^*} \quad\quad\quad (3.71)$$
이 식을 이용하면 (3.69)식은 다음과 같이 된다.
$$g_c(E) = \frac{4\pi(2m_n^*)^{3/2}}{h^3} \sqrt{E - E_c} \quad\quad\quad (3.72)$$
위 식은 $E > E_c$에서 성립한다.
• Valence 밴드 상단에 있는 hole의 상태 밀도
valence 밴드 하단에 대해서 $E$-$k$ diagram을 다음과 같이 표현할 수 있다.
$$ E= E_v - \frac{\hbar^2 k^2}{2m_p^*} \quad\quad\quad (3.73) $$
$m_p$: 전자의 유효질량.
전자의 DOS(density of state, 상태 밀도)를 구할 때와 유사한 절차를 따라서 다음을 얻는다.
$$g_v(E) = \frac{4\pi(2m_p^*)^{3/2}}{h^3} \sqrt{E_v - E} \quad\quad\quad (3.75) $$
위 식은 $E < E_v$에서 성립한다.
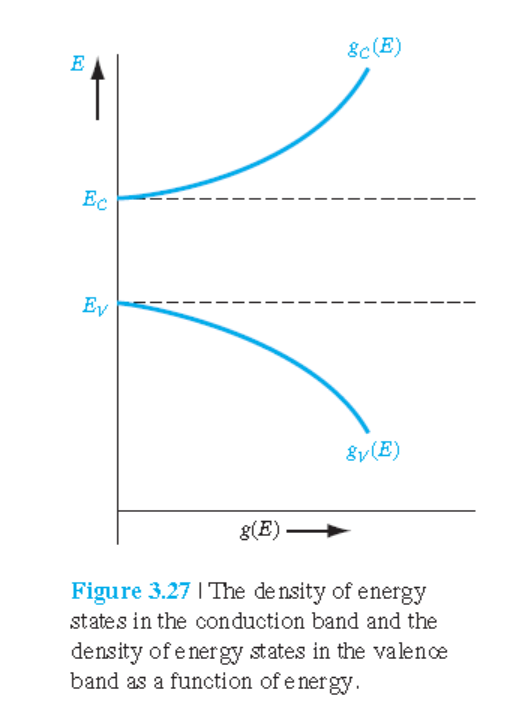
전자와 hole의 유효질량가 같다면,
전자와 hole에 대한 g(E) 곡선은 $E_{\mathrm{midgap}}$을 기준으로 대칭이 될 것이다.
3.5 통계 역학
단위 에너지당 단위 부피당 에너지 $E$를 가진 입자들의 수($N(E)$)는 다음과 같이 주어진다.
$N(E) = g(E)f(E)$
$N(E)$: 단위에너지당 입자들의 수 밀도
$f(E)$는 분포함수라고 한다.
추가내용
단위부피당 전체 입자의 수($N$)는
$$ N = 2\int_0^\infty \int_0^\infty \int_0^\infty f(E) dn_x dn_y dn_z$$
$$ = \frac{2a^3}{\pi^3} \int_0^\infty \int_0^\infty \int_0^\infty f(E) dk_x dk_y dk_z$$
$$ \rightarrow 2\int_0^\infty g(E)f(E) dE$$
$$ \rightarrow \quad N(E) = g(E)f(E) $$
$N(E)$를 구하기 위해서는 $f(E)$를 추가적으로 결정해야한다.
3.5.1 통계 법칙
• Maxwell-Boltzmann 분포
$$ f_{\textrm{MB}} = A e^{-E/kT} $$
• Bose-Einstein 분포
$$ f_{\textrm{BE}} = \frac{1}{e^{(E-E_F)/kT} - 1} $$
• Fermi-Dirac 분포
$$ f_{\textrm{FD}} = \frac{1}{e^{(E-E_F)/kT} + 1} $$
3.5.2 Fermi–Dirac 확률 함수
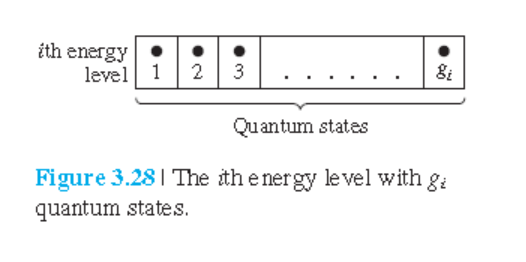
그림 3.28은 $g_i$의 양자상태를 갖는 $i$번째 에너지 준위를 보여준다.
Pauli배타원리에 의하면 각 양자상태는 비어있거나 1개의 입자만 존재할 수 있다.
$i$번째 준위에 있는 입자의 수를 $N_i$개라고 하면
1번째 입자를 양자상태들에 넣을 수 있는 방법의 수는 $g_i$개,
2번째 입자를 양자상태들에 넣을 수 있는 방법의 수는 $g_i-1$개,
...
$N_i$번째 입자를 양자상태들에 넣을 수 있는 방법의 수는 $g_i-(N_i-1)$개이다.
그러면 $i$번째 에너지 준위에서 $N_i$개의 입자를 배열할 수 있는 방법의 수는 다음과 같다.
$$ (g_i)(g_i-1)\cdots (g_i-(N_i-1)) = \frac{g_i !}{(g_i-N_i)!} $$
입자들을 서로 구별할 수 없다면, 실제 배열할 수 있는 방법의 수는 다음과 같다.
$$ W_i = \frac{g_i !}{N_i !(g_i-N_i)!} \quad\quad (3.77)$$
입자가 존재하는 에너지준위의 수가 모두 $n$개 라고 하고,
각 준위에 존재하는 구별할 수 없는 입자의 수가 $(N_1,N_2,N_3,...,N_n)$로 주어진다면,
모든 준위에 존재하는 입자들을 배열할 수 있는 가능한 모든 방법의 수는 다음과 같이 주어진다.
$$ W = \prod_{i = 1}^{n} \frac{g_i !}{N_i !(g_i-N_i)!} \quad\quad (3.78)$$
입자의 총수가 $N$개라고 하면, $N=\sum_{i=1}^{n}N_i$ 이다.
최대확률분포를 계산하기 위해 $W$가 최대가 되는 조건을 찾는다.
총에너지 $E=\sum_{i=1}^{n}E_i$와 전체 개수 $N$은 일정한 값으로 유지한채
$E_i$와 $N_i$을 변화시켜가면서 $W$를 최대가 되는 조건을 찾으면 다음과 같은 식을 얻는다.
$$ \frac{N(E)}{g(E)} = f_F(E) = \frac{1}{1+e^{(E-E_F)/kT}} $$
$f_F(E)$(Fermi-Dirac 분포)
: 에너지 $E$에 있는 하나의 양자 상태를 전자가 차지할 확률.
: 어느 에너지 $E$에 있는 총 양자상태중에 전자로 채워진 양자상태의 비율.
여기서 $E_F$는 Fermi 에너지이다.
3.5.3 분포함수와 Fermi 에너지
• $T = 0$ K 에서
Fermi 에너지의 정의는 아래 그림에서 명확하다.
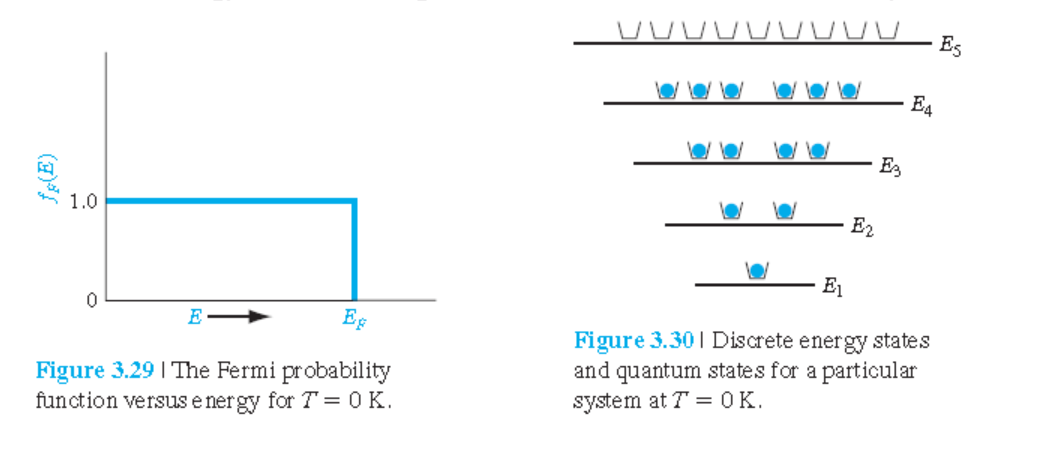
그림 3.29: 온도가 0 K일 때, Fermi-Dirac 분포함수.
그림 3.30: 온도가 0 K일 때, 에너지 준위들에 배열된 전자들의 분포
에너지가 높아짏수록 상태수가 많아지는 것은 그림 3.26과 연계해서 이해할 수 있다.
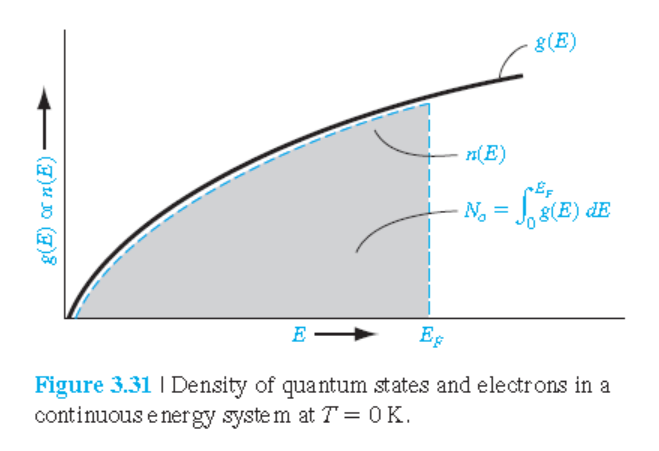
에너지가 높아짏수록 상태수가 많아지는 것은 위 그림으로 다시 이해할 수 있다.
Fermi 에너지 : 온도가 0 K에서 전자가 채워질 수 있는 최고 에너지
• $T > 0$ K 에서
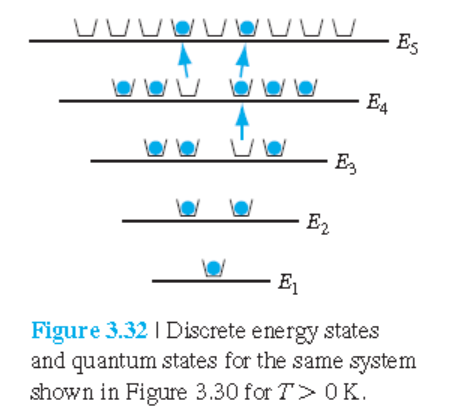
그림 3.32: $T > 0$일 때, 에너지 준위들에 배열된 전자들의 분포.
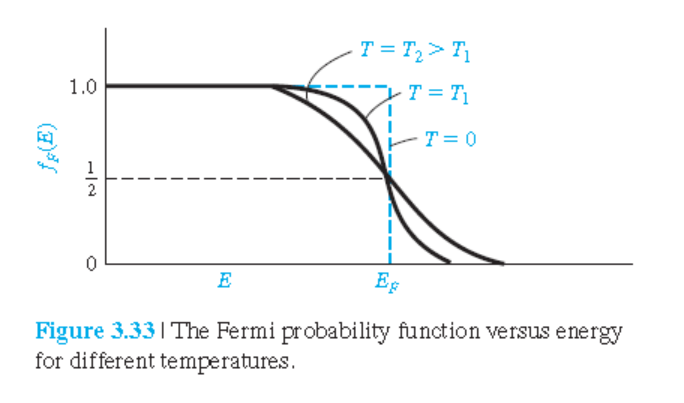
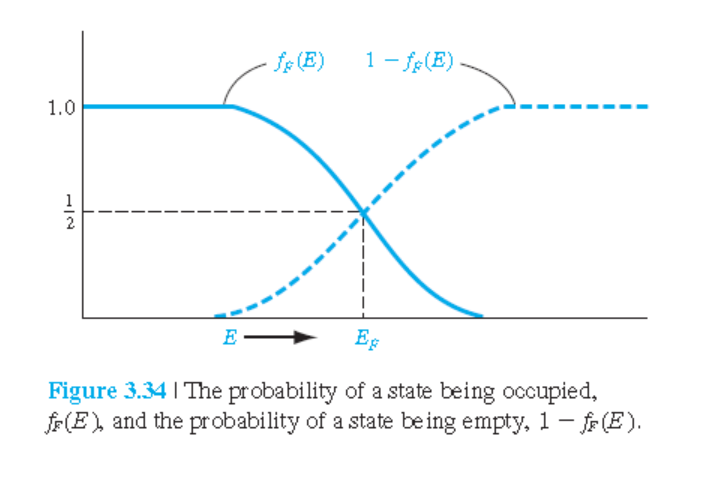
그림 3.33: $T > 0$일 때, Fermi-Dirac 분포함수.
$T > 0$일 때, $E=E_F$에서의 Fermi-Dirac 분포함수는 $\frac{1}{2}$이다.
$$ f_F(E=E_F) = \frac{1}{1+e^0} = \frac{1}{2} $$
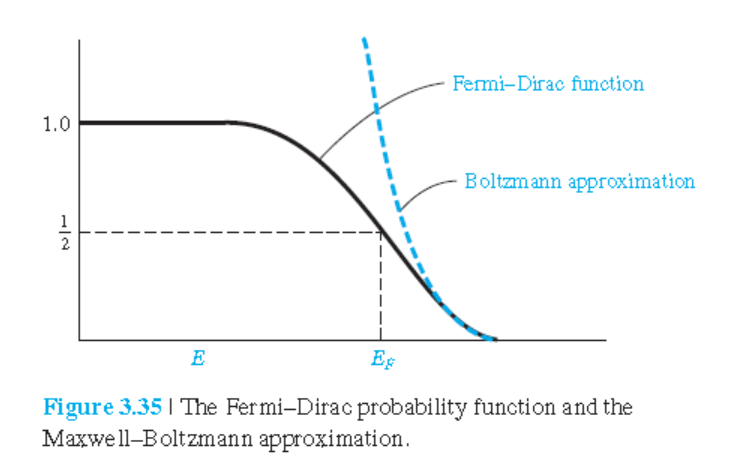
• Maxwell-Boltzmann 근사
$E-E_F>>kT$인 경우에 Fermi-Dirac 분포함수는 다음 식으로 근사된다.
$$ f_F(E) \approx e^{-(E-E_F)/kT} $$
이 식은 Fermi-Dirac 분포함수의 Maxwell-Boltzmann 근사라고 한다.
그림 3.35는 Fermi-Dirac 분포함수와 Maxwell-Boltzmann 근사를 보여준다.
