4. 평형상태의 반도체
4.1 반도체에서 전하 운반자(charge carrier)
4.1.1 전자와 hole의 평형 분포
• 전류를 구하기위해서 carrier의 수를 결정하는 것이 중요하다.
• Conduction 밴드 내의 전자 농도(electron concentration)의 (에너지) 분포
$$
n(E)=g_c(E) f_F(E) \qquad (4.1)
$$
• Valence 밴드 내의 hole 농도(hole concentration)의 (에너지) 분포
$$
p(E)=g_v(E)\left(1-f_F(E)\right) \qquad (4.2)
$$
Carrier 농도를 구하기 위해 $E_c$, $E_v$, $E_F$를 결정할 필요가 있다.
불순물과 결함이 전혀 없는 intrinsic(진성) 반도체에서 $T = 0$ K에서 valence 밴드를 가득채우고
conduction 밴드는 비어있다는 것을 2장에서 논의했다.
이것은 $E_F$가 $E_c$과 $E_v$ 사이에 존재한다는 것을 의미한다.
온도가 상승하면 valence 밴드내 전자가 conduction 밴드로 올라가고, valence 밴드내에 hole이 발생한다.
intrinsic 반도체에서는 전자가 생긴만큼 hole이 생기기 때문에,
Conduction 밴드내의 전자수와 valence 밴드내에 hole의 수는 같다.
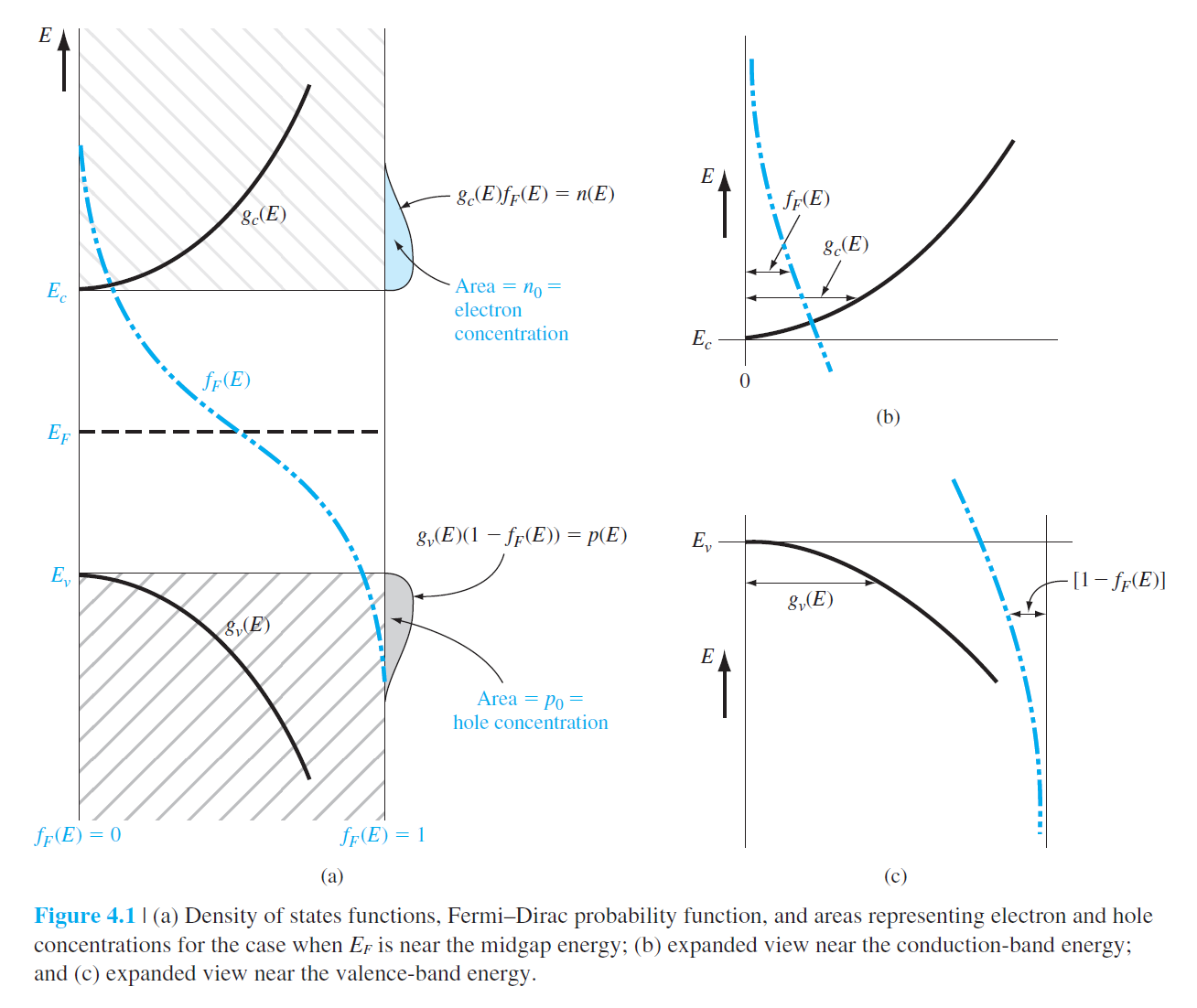
유효질량이 같으면 $g_c$와 $g_v$는 대칭이 된다.
이 경우 $E_F$는 $E_c$과 $E_v$ 사이에 중간 값에 해당한다(4.1.4에서 증명).
4.1.2 $n_0$와 $p_0$
• 열평형 전자 농도
Conduction 밴드에 있는 전자의 농도는 다음과 같이 주어진다.
$$
n_0 =\int g_c(E) f_F(E) d E \qquad (4.3)
$$
Fermi-Dirac 분포를 다음과 같이 Maxwell 분포로 근사한다.
\begin{equation}
\begin{aligned}
&f_F(E) =\frac{1}{1+\exp \frac{\left(E-E_F\right)}{k T}} \approx \exp \left[\frac{-\left(E-E_F\right)}{k T}\right] \qquad (4.4)\\[10pt]
&n_0 =\int_{E_c}^{\infty} \frac{4 \pi\left(2 m_n^*\right)^{3 / 2}}{h^3} \sqrt{E-E_c} \exp \left[\frac{-\left(E-E_F\right)}{k T}\right] d E \\[10pt]
& (4.5)\\[10pt]
&\eta =\frac{E-E_c}{k T} \qquad (4.6)\\[10pt]
&n_0 =\frac{4 \pi\left(2 m_n^* k T\right)^{3 / 2}}{h^3} \exp \left[\frac{-\left(E_c-E_F\right)}{k T}\right] \int_0^{\infty} \eta^{1 / 2} \exp (-\eta) d \eta \\[10pt]
& (4.7)
\end{aligned}
\end{equation}
다음의 Gamma 함수를 활용하면
\begin{equation}
\begin{aligned}
\int_0^{\infty} \eta^{1 / 2} \exp (-\eta) d \eta=\frac{1}{2} \sqrt{\pi} \qquad (4.8)
\end{aligned}
\end{equation}
$n_0$는 다음과 같이 주어진다.
$$
n_0=2\left(\frac{2 \pi m_n^* k T}{h^2}\right)^{3 / 2} \exp \left[\frac{-\left(E_c-E_F\right)}{k T}\right]
$$
여기서 위 식의 복잡한 상수 집단을 다음과 같이 두면,
$$
N_c=2\left(\frac{2 \pi m_n^* k T}{h^2}\right)^{3 / 2}
$$
$n_0$는 다음과 같이 간략하게 주어진다.
$$ n_0=N_c \exp \left[\frac{-\left(E_c-E_F\right)}{k T}\right] \qquad (4.11) $$
$N_c$는 conduction 밴드에서 유효 상태 밀도라고 한다.
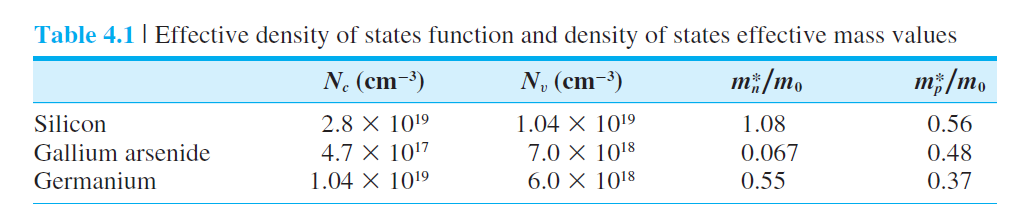
표 4.1에 의하면 $N_c=2.5 \times 10^{19} \mathrm{~cm}^{-3}$ 으로 주어진다.
• 열평형 hole 농도
Valence 밴드에 있는 hole의 농도는 다음과 같이 주어진다.
$$
p_0=\int g_v(E)\left[1-f_F(E)\right] d E \qquad (4.12)
$$
전자의 경우와 유사하게 $p_0$는 다음과 같이 간략하게 주어진다.
$$
p_0=N_v \exp \left[\frac{-\left(E_F-E_v\right)}{k T}\right] \qquad (4.19)
$$
여기서 $N_v$는 valence 밴드에서 유효 상태밀도하고 하고,
$$
N_v=2\left(\frac{2 \pi m_p^* k T}{h^2}\right)^{3 / 2} \qquad (4.18)
$$
표 4.1에서는 $N_v = 10^{19} \mathrm{cm}^{-3}$로 주어진다.
(GaAs의 $N_v$를 주의한다.)
4.1.3 Intrinsic carrier 농도
Intrinsic(진성) 반도체의 Fermi level을 $E_{Fi}$로 표기하자.
\begin{equation}
\begin{aligned}
&n_0 = n_i=N_c \exp \left[\frac{-\left(E_c-E_{F i}\right)}{k T}\right] \qquad (4.20)\\[10pt]
&p_0 = p_i=n_i=N_v \exp \left[\frac{-\left(E_{F i}-E_v\right)}{k T}\right] \qquad (4.21)\\[10pt]
&n_i^2 = N_c N_v \exp \left[\frac{-\left(E_c-E_{F i}\right)}{k T}\right] \cdot \exp \left[\frac{-\left(E_{F i}-E_v\right)}{k T}\right]\\[10pt]
& (4.22)\\[10pt]
&n_i^2 = N_c N_v \exp \left[\frac{-\left(E_c-E_v\right)}{k T}\right]=N_c N_v \exp \left[\frac{-E_g}{k T}\right] \\[10pt]
& (4.23)
\end{aligned}
\end{equation}
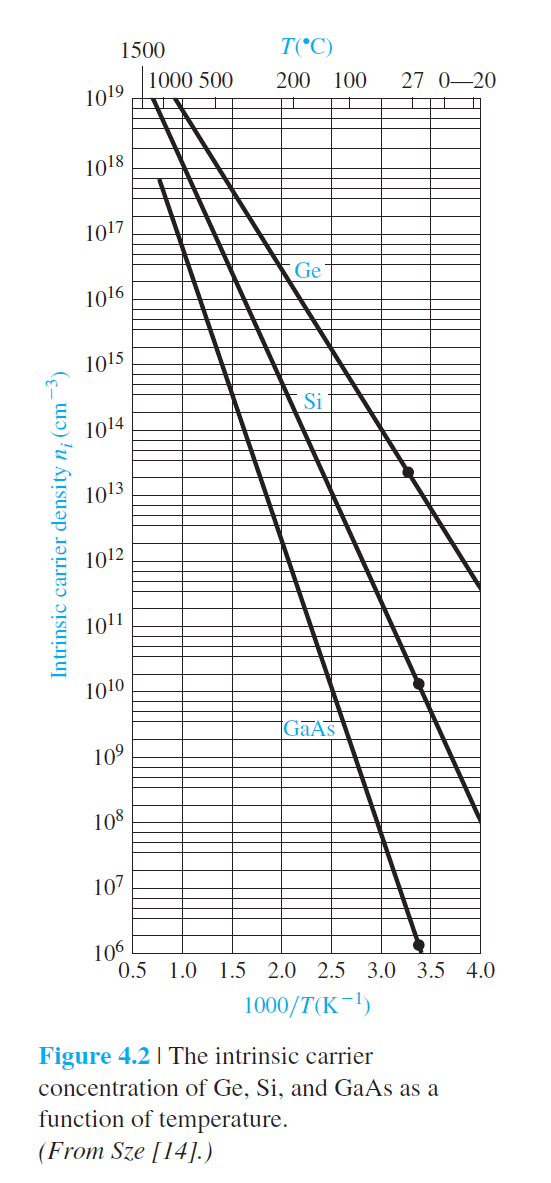
결과적으로 $n_i$는 에너지의 함수로 주어지긴 하지만 $E_c$, $E_v$, $E_{F i}$의 값들은 필요없이 에너지 갭($E_g$)만으로 주어질 수 있다.
실험값과 차이는 있으나 심각한 오차는 아니다.
4.1.4 Intrinsic Fermi-준위 위치
반도체에서 0이 아닌 어떤 온도에서 valence band의 전자가 conduction band로 올라가는데,
Intrinsic 반도체에서는 valence band에서 비워진만큼 conduction band에 채워지기 때문에 $n_0 = p_0$ 가 성립한다.
그래서 다음이 얻어진다.
\begin{aligned}
& N_c \exp \left[\frac{-\left(E_c-E_{F i}\right)}{k T}\right]=N_v \exp \left[\frac{-\left(E_{F i}-E_v\right)}{k T}\right] \quad (4.24)\\[10pt]
& E_{F i}=\frac{1}{2}\left(E_c+E_v\right)+\frac{1}{2} k T \ln \left(\frac{N_v}{N_c}\right) \qquad (4.25)\\[10pt]
& E_{F i}=\frac{1}{2}\left(E_c+E_v\right)+\frac{3}{4} k T \ln \left(\frac{m_p^*}{m_*^*}\right) \qquad (4.26a)
\end{aligned}
다음과 같이 두면
$$\frac{1}{2}\left(E_c+E_v\right)=E_{\text {midgap }} $$
다음 식이 얻어진다.
$$ E_{F i}-E_{\text {midgap }}=\frac{3}{4} k T \ln \left(\frac{m_p^*}{m_n^*}\right) \qquad (4.26a) $$
$m_n^*$와 $m_p^*$사이의 관계에 따라 $E_{F i}$의 위치는 다음과 같이 주어진다.
$m_n^* = m_p^*$ : $E_{F i} = E_{\text {midgap }}$
$m_n^* > m_p^*$ : $E_{F i} < E_{\text {midgap }}$
$m_n^* < m_p^*$ : $E_{F i} > E_{\text {midgap }}$
4.2 Dopant 원자와 에너지 준위
Dopant 원자 : doping 되는 원자.
불순물 첨가 반도체 : extrinsic(외인성) semiconductor
4.2.1 정량적 기술
5족원소 $P$ doping
5번째 가전자 : donor
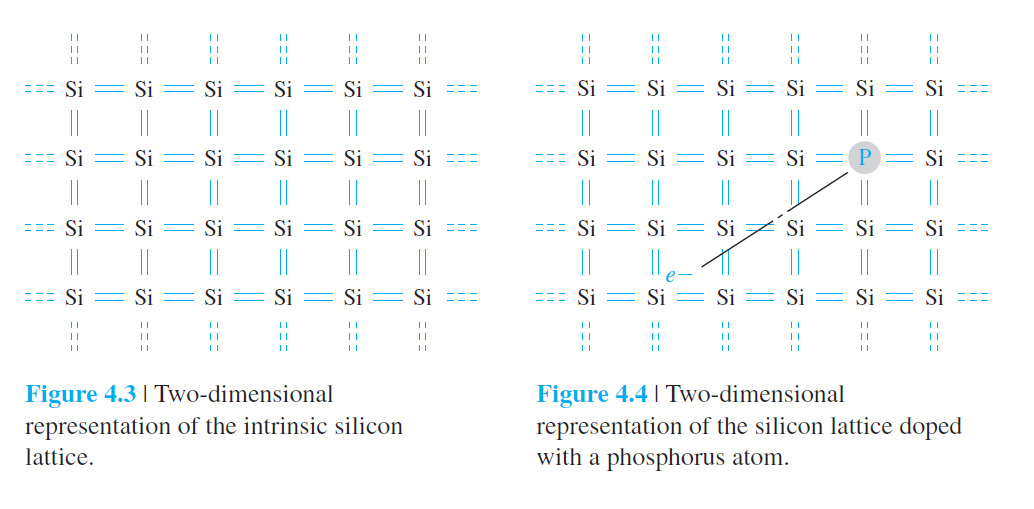
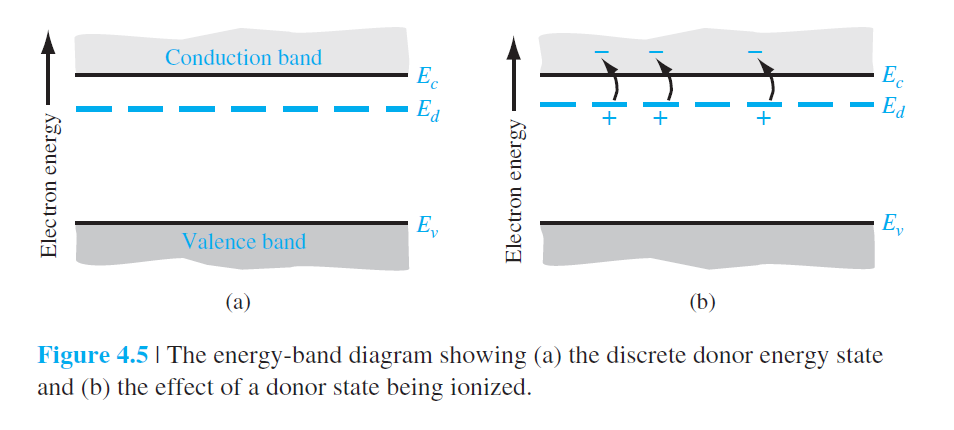
$E_d$ : donor의 에너지 준위. 여기에 위치하는 이유
donor impurity
n type 반도체
3족원소 $B$ doping
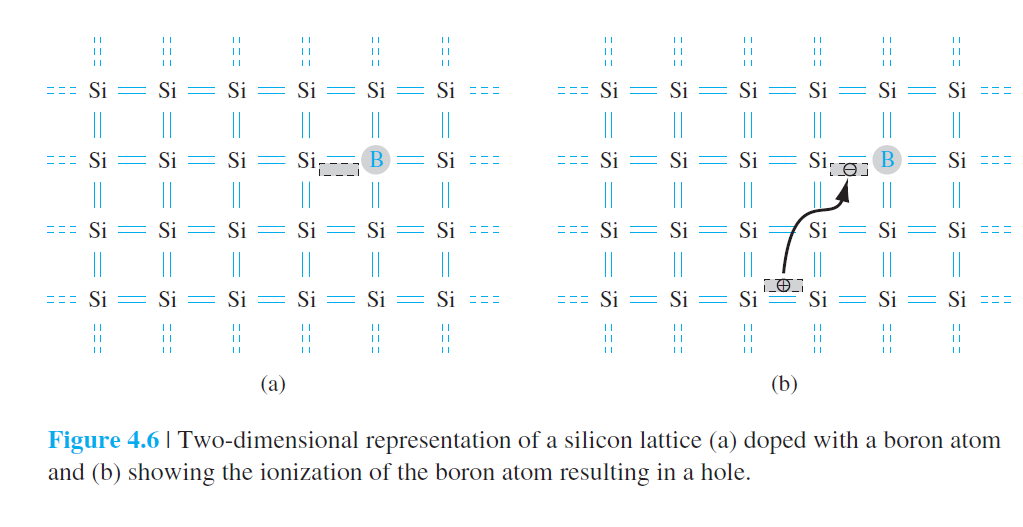
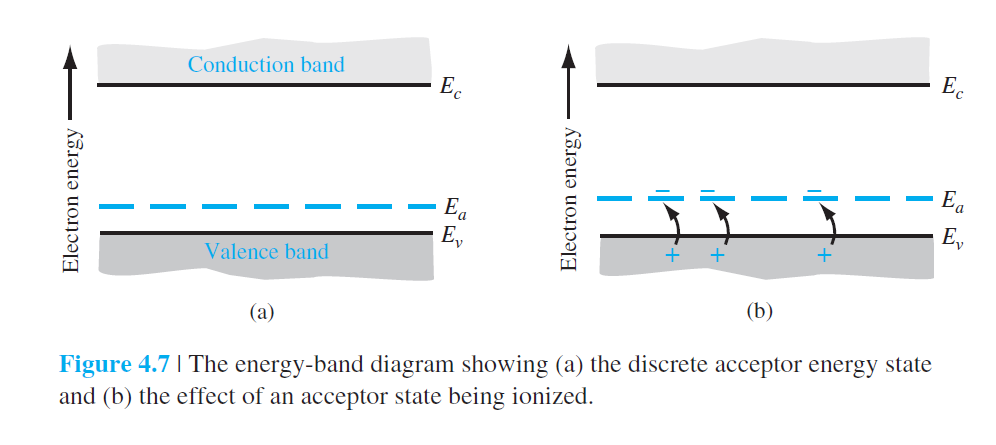$E_a$ : acceptor의 에너지 준위. 여기에 위치하는 이유
acceptor impurity
p type 반도체
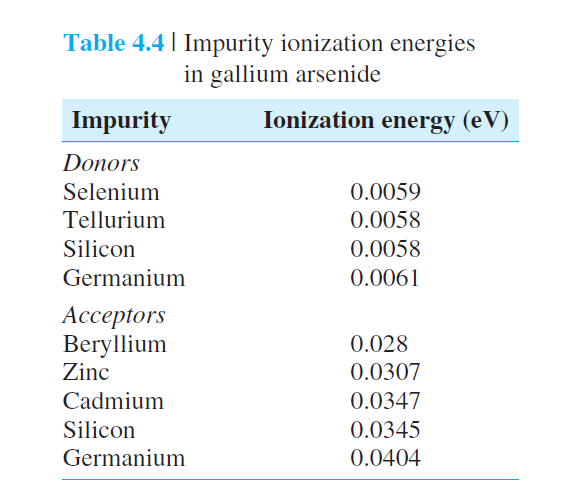
4.2.2 Ionization Energy
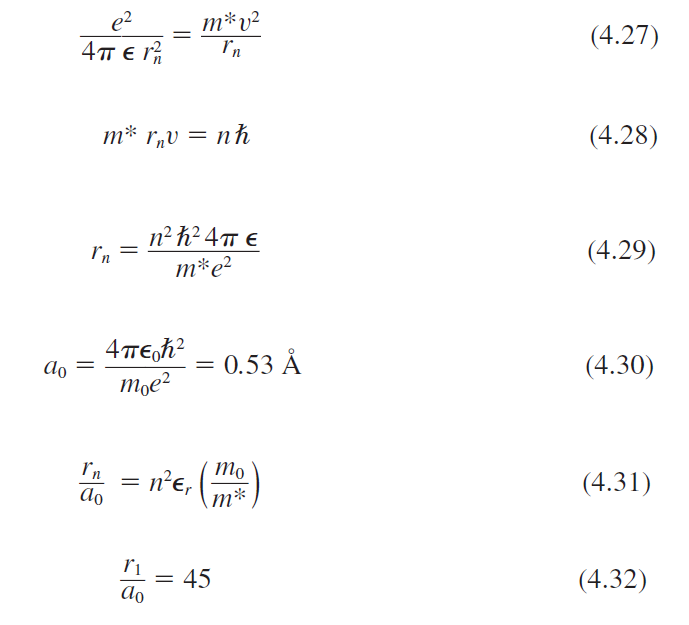
각운동량의 양자화.
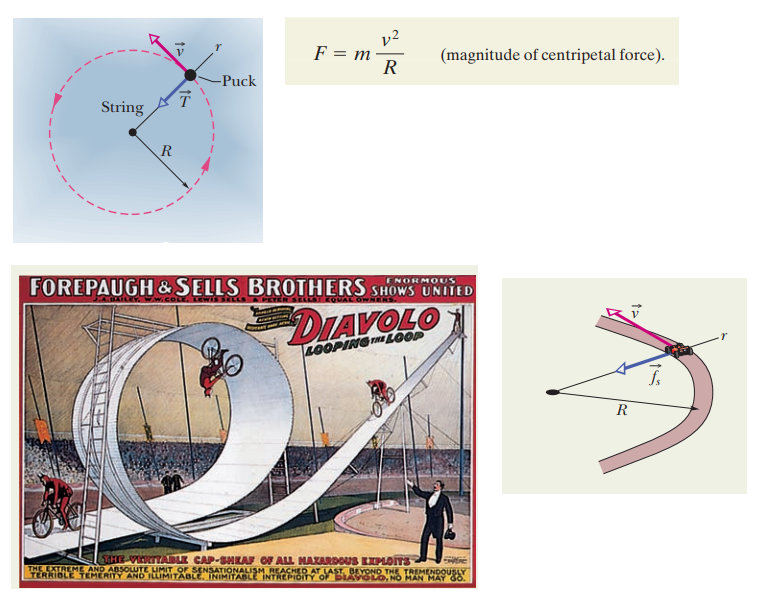
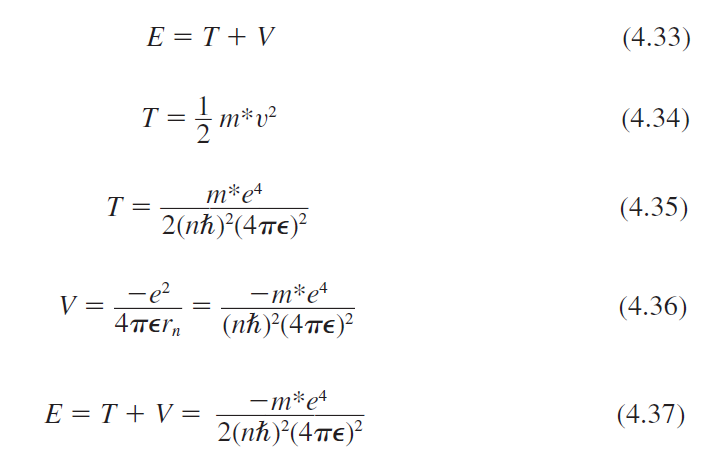
(2.73)식과 유사. 유효질량, 유전율 변경.
 |
 |
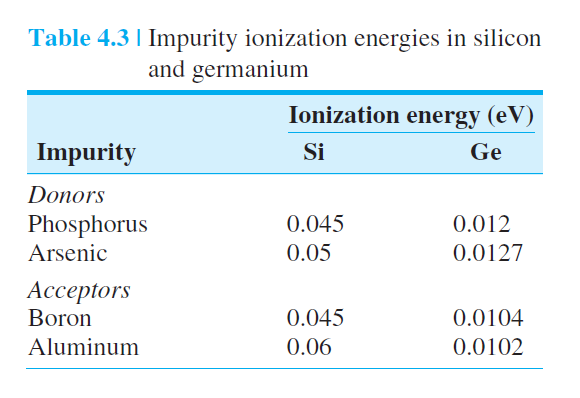4.2.3 III–V 족 반도체
• IV족 반도체에 도핑이라는 것은 IV족 원소에 III족 또는 V족 원소를 치환하는 것을 의미한다.
• III-V족 반도체에 도핑은 다음을 의미한다.
- III족 원소에 II족 또는 V족 원소에 VI족 원소를 치환
- III-V족 반도체에 IV족 원소를 치환하는 것도 도핑이라고 할수있다.
이 경우 IV족 원소가 III족 원소를 치환할수도 있고($n$-형),
V족 원소를 치환($p$-형)할수도 있다.
이러한 불순물들은 양쪽성(amphoteric)을 가지고 있다고 한다.
실험적으로 Si은 주로 donor, Ge은 accepter가 됨.
4.3 Extrinsic(외인성) 반도체
4.3.1 전자와 hole의 평형 분포
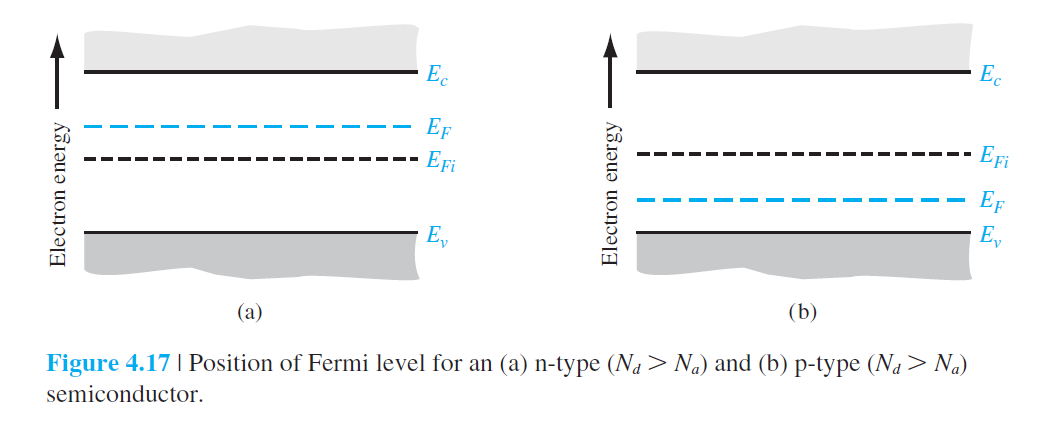
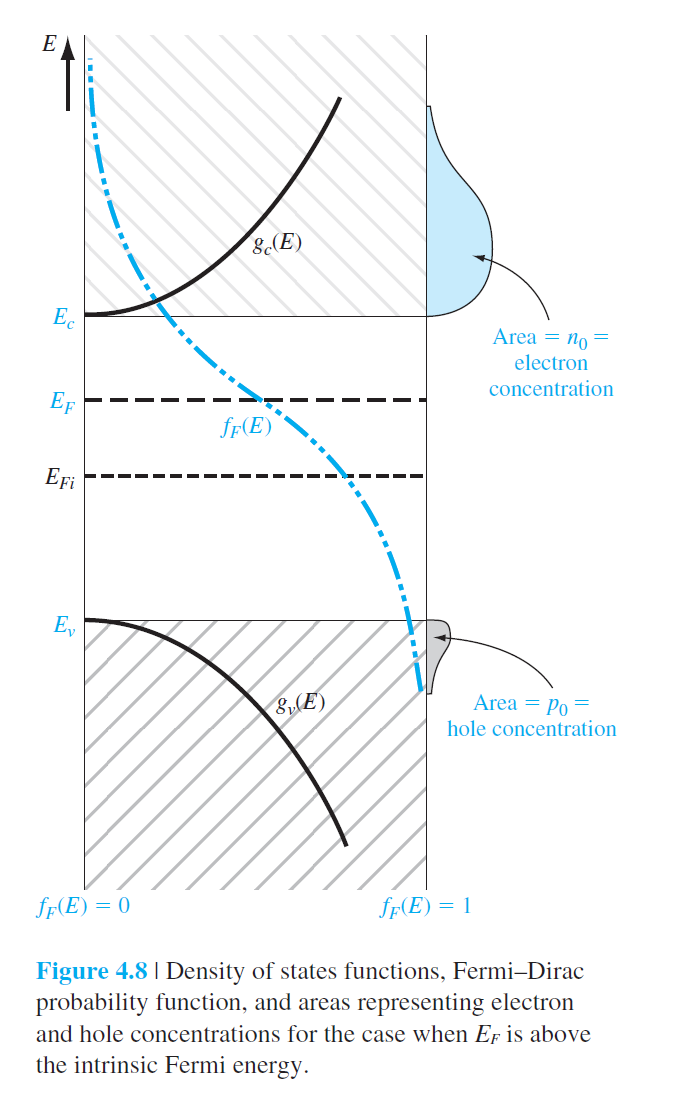 • $E_F > E_{Fi}$인 경우 $n_0 > p_0$ : n type 반도체 전자 : 다수(majority) carrier hole : 소수(minority) carrier |
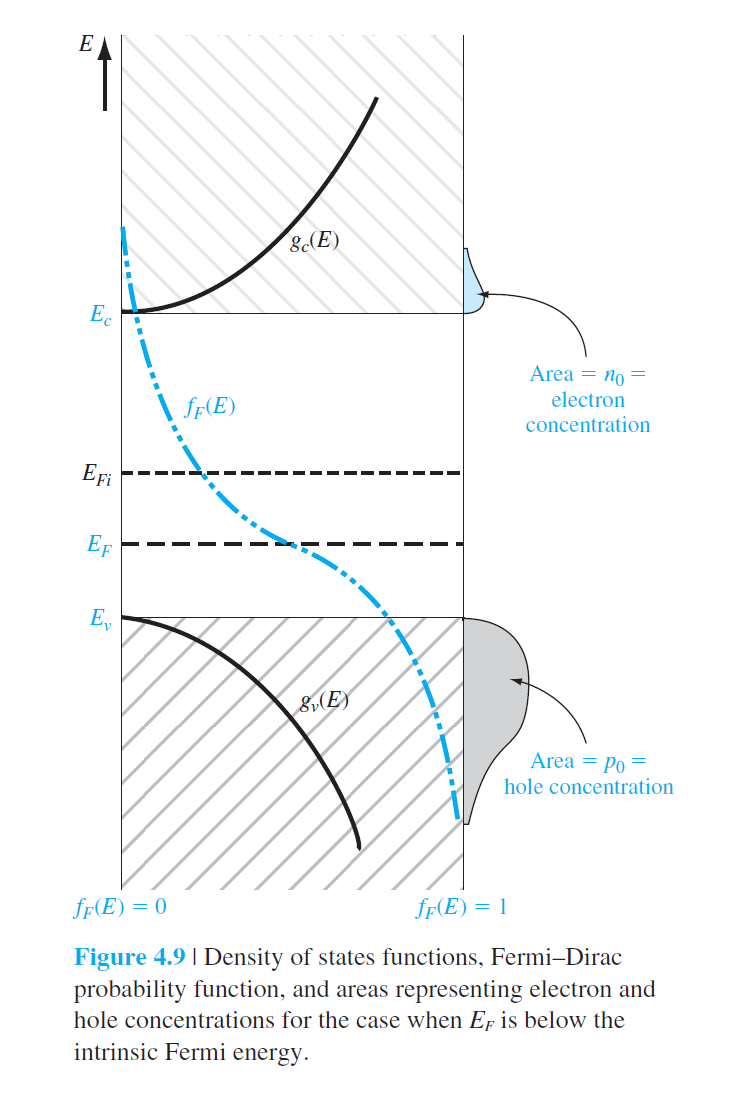 • $E_F < E_{Fi}$인 경우 $n_0 < p_0$ : p type 반도체 전자 : 소수(minority) carrier hole : 다수(majority) carrier |
(4.11) (4.19) 식 참조
• 전자와 hole 농도를 진성반도체의 정보가 포함되도록 표현할 수 있다.
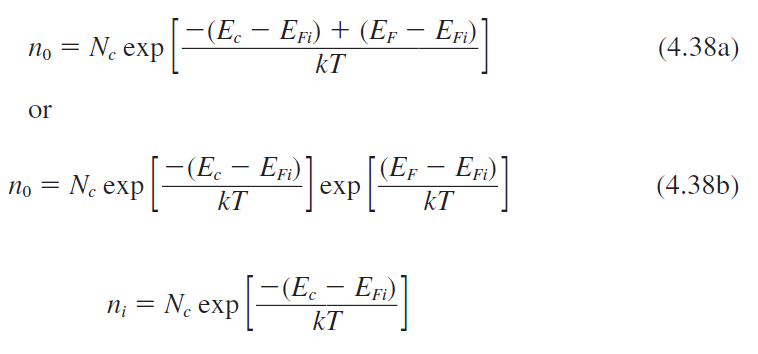
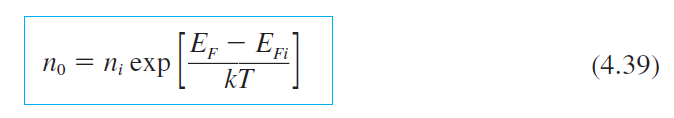
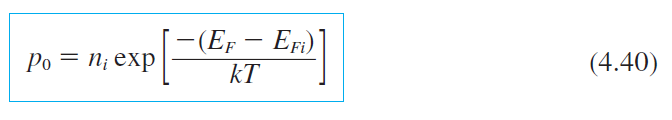
• $E_F > E_{Fi}$인 경우
$n_0 > n_i$, $p_0 < n_i$ → $n_0 > p_0$
• $E_F < E_{Fi}$인 경우
$n_0 < n_i$, $p_0 > n_i$ → $n_0 < p_0$
4.3.2 $n_0 p_0$(mass action law)
\begin{equation}
\begin{aligned}
n_0 p_0 & = N_c N_v \exp \left[\frac{-\left(E_c-E_F\right)}{k T}\right] \exp \left[\frac{-\left(E_F-E_v\right)}{k T}\right] \\
& (4.41) \\
n_0 p_0 & = N_c N_v \exp \left[\frac{-E_g}{k T}\right] \qquad (4.42)
\end{aligned}
\end{equation}
위 식의 우변은 $n_i^2$과 같음을 우리는 이미 알고 있다.
그러므로 다음이 성립한다.
$n_0 p_0 = n_i^2$ (4.43)
$n_0 p_0$는 주어진 온도에서 상수이며 반도체의 근본원리중 하나이다. 단 Boltzmann근사가 아니면 성립하지 않는다.
*4.3.3 Fermi–Dirac 적분
4.3.4 Degenerate 그리고 nondegenerate 반도체
• Nondegenerate 반도체
- Doping 농도가 낮아서 donor끼리 혹은 accepter 끼리 상호 간섭이 없다.
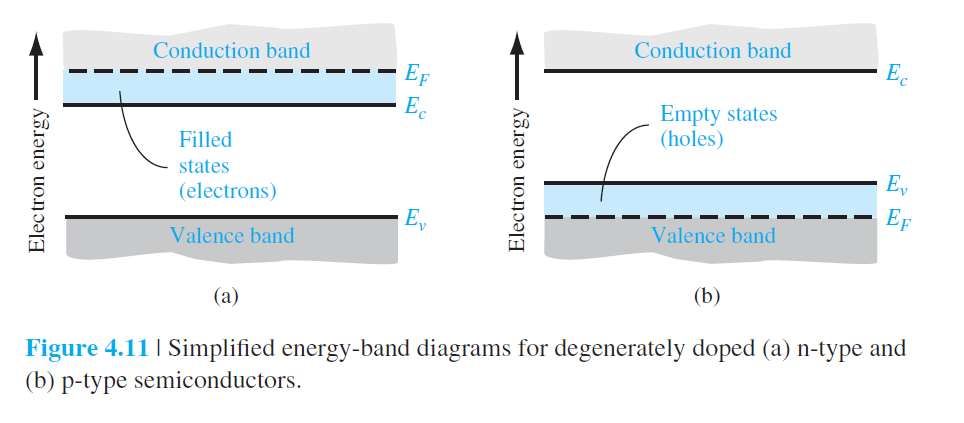
• Degenerate 반도체
- Doping 농도가 높아서 donor끼리 혹은 accepter 끼리 상호 간섭이 있다.
- 불순물 밴드를 형성할 수 있다.
- Doping 농도가 더욱 증가할 수록, $E_F$가 위로 증가하다가 $E_c$보다 위에 있게 된다.
이것은 $n_0 > N_c$일 때 발생한다. (4.11) 참조.
$$ n_0 = N_c e^{-(E_c-E_F)/(kT)}$$
4.4 Donor와 acceptor의 통계
4.4.1 확율 함수
각 Donor 준위는 donor 전자에 대해 두 가지 스핀 방향을 가지고 있어서,
두 가지 양자상태를 가지고 있다.
각 donor 준위는 한 방향의 스핀을 가진 전자들을 먼저 채우고
반대 방향의 스핀을 가진 전자들을 채운다.
Donor 불순물은 donor 전자를 하나만 갖기 때문에,
각 donor 준위는 두 가지 양자상태를 가지지만 하나만 채우기 때문에,
원래의 Fermi-Dirac 분포와는 약간 다른 분포를 갖는다.
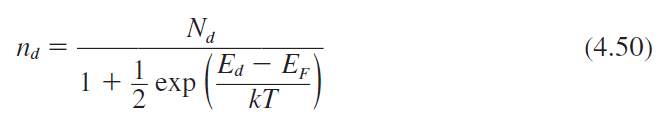
$n_d$ : donor 준위를 차지하는 electron concentration(전자농도)
$N_d$ : donor 원자의 concentration
$E_d$ : donor 준위의 에너지
$1/2$ : $1/g$, $g$ degeneracy factor
$N_d^+$ : 이온화된 donor 원자의 concentration
Accepter 원자에 대한 식
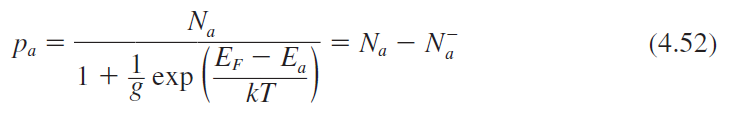
$n_d$ : accepter 준위를 차지하는 hole concentration
$N_d$ : accepter 원자의 concentration
$E_d$ : accepter 준위의 에너지
$g\approx 4$ : Si, GaAs
4.4.2 완전이온화(complete ionization)와 동결(freeze-out)
• Doner 준위를 가진 전자의 농도와 conduction 밴드에 있는 전자의 농도를 Boltzmann 근사로 구해보면 다음과 같다.
\begin{equation}
n_d \approx \frac{N_d}{\frac{1}{2} \exp \left(\frac{E_d-E_F}{k T}\right)}=2 N_d \exp \left[\frac{-\left(E_d-E_F\right)}{k T}\right]
\end{equation}
(4.53)
$$n_0 = N_c e^{-(E_c-E_F)/(kT)}$$
• 총전자수 대비 donor 전자수의 비율은 다음과 같다.
\begin{equation}
\begin{aligned}
&\frac{n_d}{n_d+n_0}=\frac{2 N_d \exp \left[\frac{-\left(E_d-E_F\right)}{k T}\right]}{2 N_d \exp \left[\frac{-\left(E_d-E_F\right)}{k T}\right]+N_c \exp \left[\frac{-\left(E_c-E_F\right)}{k T}\right]} \\
& (4.54)\\
&\frac{n_d}{n_d+n_0}=\frac{1}{1+\frac{N_c}{2 N_d} \exp \left[\frac{-\left(E_c-E_d\right)}{k T}\right]} \qquad (4.55)
\end{aligned}
\end{equation}
$E_c-E_d$ : donor전자의 이온화 에너지
상온에서는 donor 상태는 본질적으로 완전 이온화(complete Ionization)되고,
doping concentration $10^{16}$ cm$^{-3}$에서는 거의 대부분의 donor 불순물 원자들은 이온화된다.
상온에서 accepter 도 완전히 이온화 된다. → $p_a = 0$
그림 4.12 참조
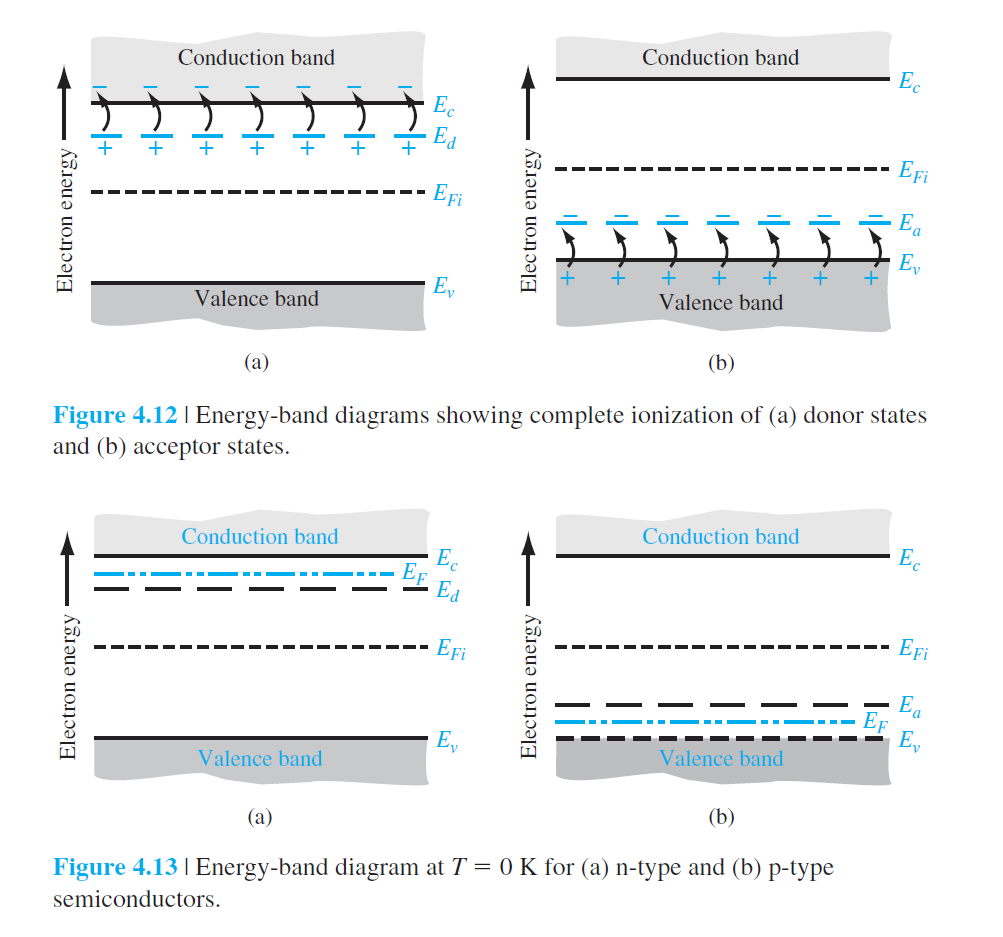
완전이온화의 반대 → $T = 0$ : 모든 전자는 가장 낮은 에너지 상태에 있음. freeze-out(동결)
n-type 반도체에서 $T = 0$
: $n_d = N_d$, $N_d^+ = 0 $
(4.50)에서 $E_F > E_d$를 의미 : $E_c$와 $E_d$의 중간 (그림 4.13 a)
p-type 반도체에서 $T = 0$
: $p_a = N_a$, $N_a^+ = 0 $
(4.52)에서 $E_F < E_a$를 의미 : $E_a$와 $E_v$의 중간 (그림 4.13 b)
$T = 0 \sim 300 K$ : donor와 acceptor의 부분 이온화
4.5 전하 중성
4.5.1 보상 반도체(Compensated semiconductor)
Compensated(보상) 반도체 : 같은 영역에 donor와 accepter impurity를 함께 도핑한 반도체(그림 4.14)
보상 n-type 반도체 : $N_d > N_a$
보상 p-type 반도체 : $N_a > N_d$
$N_d = N_a$ : completely compensated 반도체(완전보상반도체) : intrinsic 반도체의 특성
4.5.2 평형 상태에서 전자와 hole의 농도
전하 중성 조건
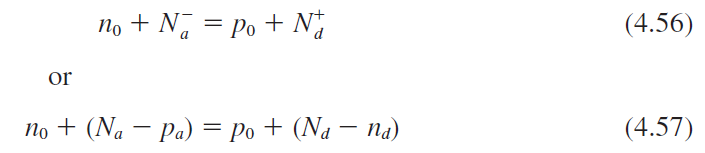
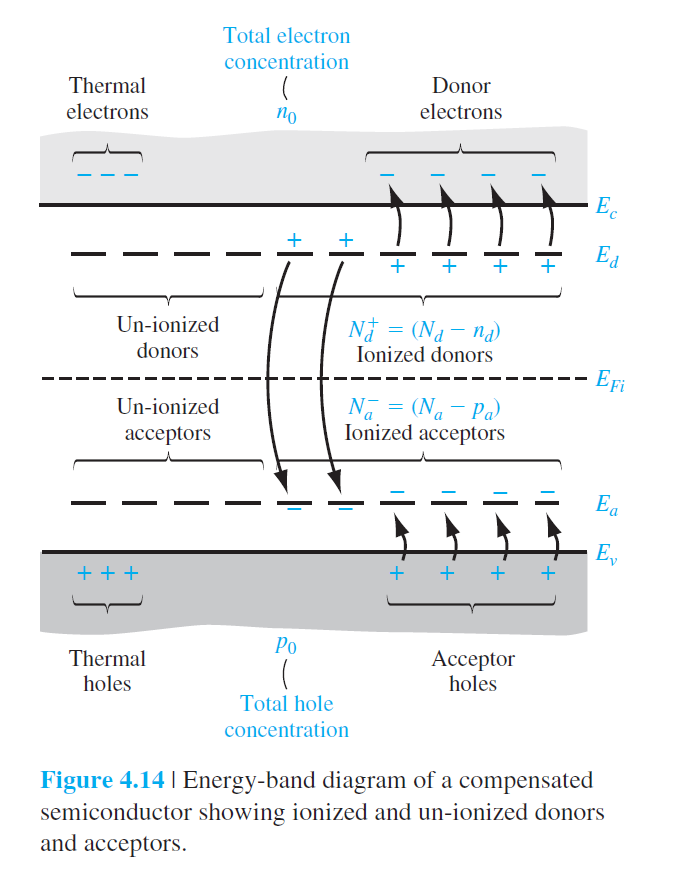
Thermal equilibrium electron concentration
완전이온화의 경우
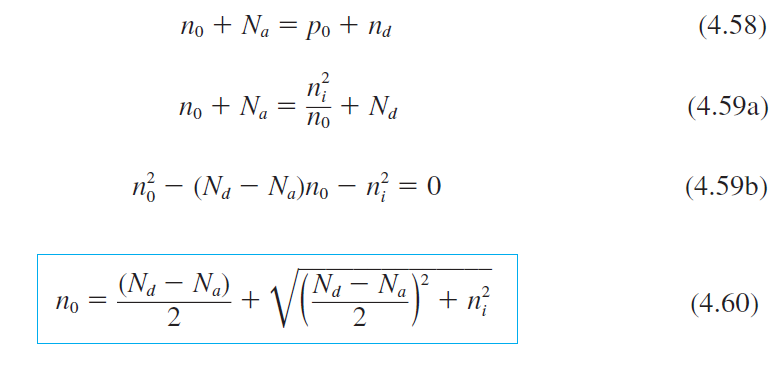
$$n_0 p_0 = n_i^2 \qquad(4.43)$$
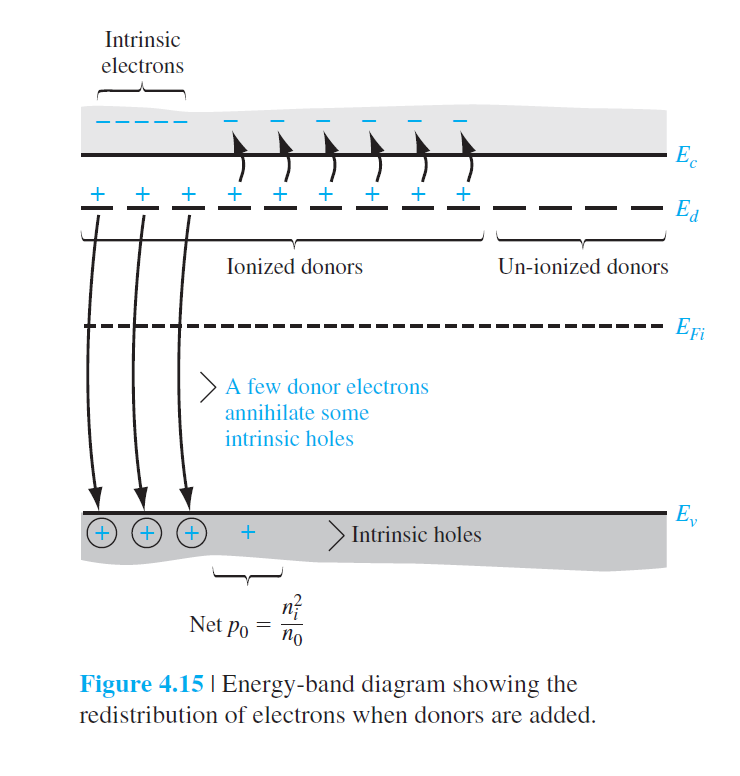
Donor가 추가되었을때 전자의 재분포
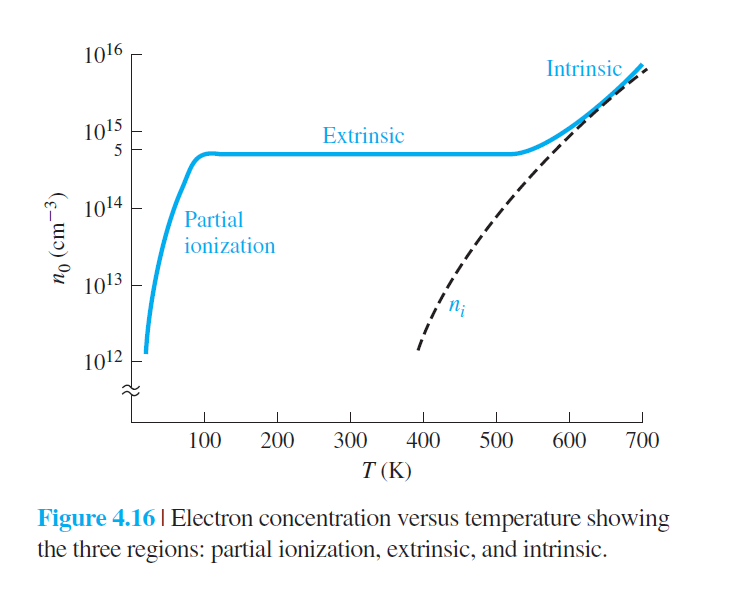
온도에 따른 electron concentration의 변화
Thermal equilibrium hole concentration
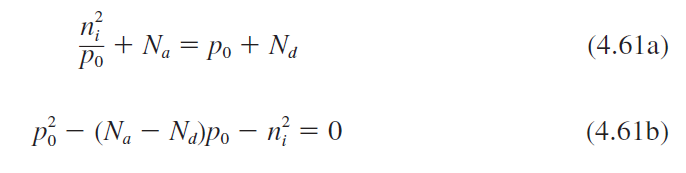
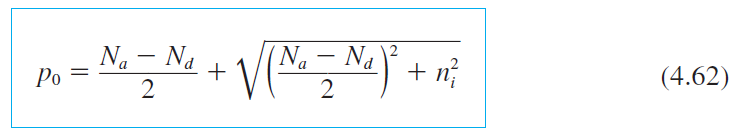
보상 p-type 반도체에 대해서 소수 carrier 전자 농도는 다음과 같이 주어진다.
$$ n_0 = \frac{n_i^2}{p_0} = \frac{n_i^2}{N_a - N_d} $$
완전 이온화의 경우 n-type 반도체에서 전자농도 : $n_0 \simeq N_d$
완전 이온화의 경우 p-type 반도체에서 hole농도 : $p_0 \simeq N_a$
완전 이온화의 경우 보상 p-type 반도체에서 hole농도
: $p_0 \simeq N_a - N_d$
n-type 반도체의 소수 carrier농도를 4.62식으로 계산 가능하나 계산상의 문제로 실질적으로는 안되고,
4.43식을 이용하여 다수 carrier 농도가 결정되면, 소수 carrier 농도를 계산한다.
예제 3.13
T = 475 K
$$n_i^2 = N_c N_v \exp\left(-\frac{E_g}{kT}\right) $$
$$ = (2.8\times 10^{19}) (1.04\times 10^{19}) \left(\frac{475}{300}\right)^3 \exp\left[-\frac{1.12}{0.0259}\left(\frac{300}{475}\right) \right] $$
$n_i = 3.99\times 10^{13}$ cm$^{-3}$
$$n_0 = \frac{N_d}{2} + \sqrt{\left(\frac{N_d}{2}\right)^2 + n_i^2} $$
$$1.03 N_d = \frac{N_d}{2} + \sqrt{\left(\frac{N_d}{2}\right)^2 + (3.99\times 10^{13})^2} $$
$N_d = 2.77\times 10^{14}$ cm$^{-3}$
4.6 Fermi 준위의 위치
4.6.1 수학적 유도
(4.11)로부터
$N_d \gg n_i$인 n-type 반도체의 경우
보상반도체의 경우 $N_d$를 $N_d-N_a$로 대체
Intrinsic 반도체에 대한 (4.39)식으로부터
보상반도체의 경우 $N_d=N_a$ → (4.60), (4.65)로 부터 $n_0 = n_i$, $E_F = E_{Fi}$
p-type에 대한 방정식
보상반도체의 경우 $N_a$를 $N_a-N_d$로 대체
(4.65) : n-type $n_0 > n_i$, $E_F > E_{Fi}$
(4.68) : p-type $p_0 > n_i$, $E_F < E_{Fi}$
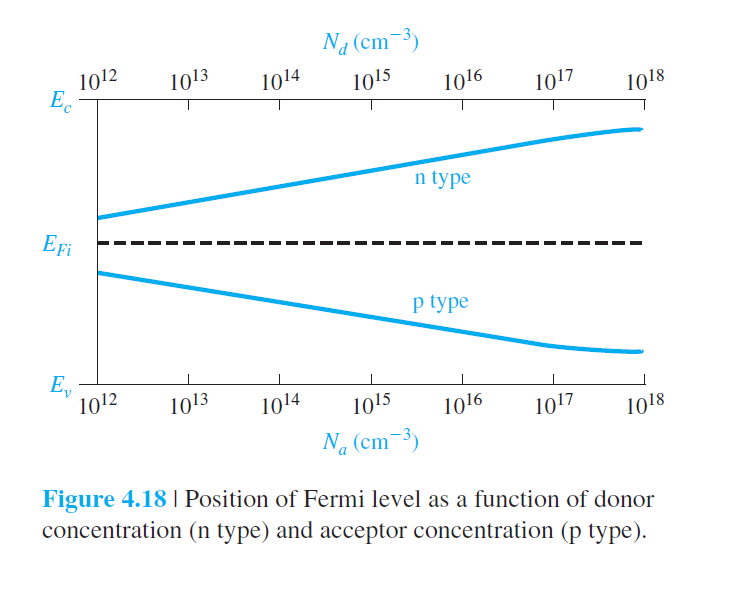
4.6.2 도핑 농도와 온도에 따른 $E_F$의 변화
Donor concentration($N_d$)과 accepter concentration($N_a$)의 변화에 따른 $E_F$
(4.64)식, (4.67)식 참조
(4.65)식과 (4.68)식에 의한 $E_F$의 온도 의존성
4.60식, 4.62식, 4.39식, 4.40식을 이용합니다.
$$n_0 = \frac{N_d - N_a}{2} + \sqrt{\left(\frac{N_d-N_a}{2}\right)^2 +n_i^2} \qquad (4.60)$$
$$n_0 = n_i e^{(E_F-E_{Fi})/kT} \qquad (4.39)$$
4.60식과 4.39식을 연립하면
$$n_i e^{(E_F-E_{Fi})/kT} = \frac{N_d - N_a}{2} + \sqrt{\left(\frac{N_d-N_a}{2}\right)^2 +n_i^2} $$
(4.39)
위 식을 로그 취해서 대략 정리하면 다음과 같다.
$$E_F - E_i \approx E_g $$
E_g는 온도가 증가할수록 감소한다(Sze 참조).
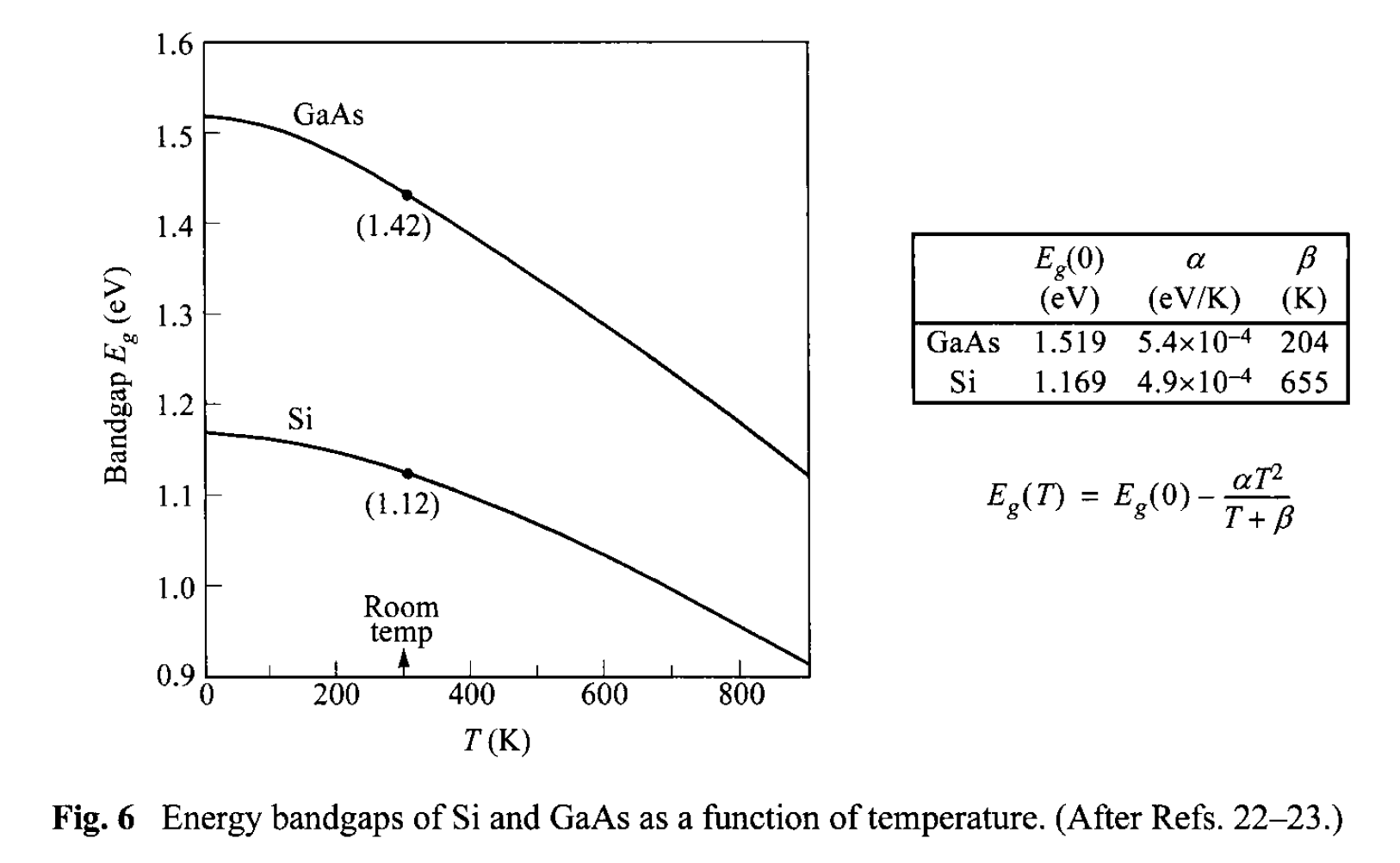
$n_i$는 온도의 함수(4.23) → (4.65), (4.68)로 부터, $E_F$도 온도의 함수.
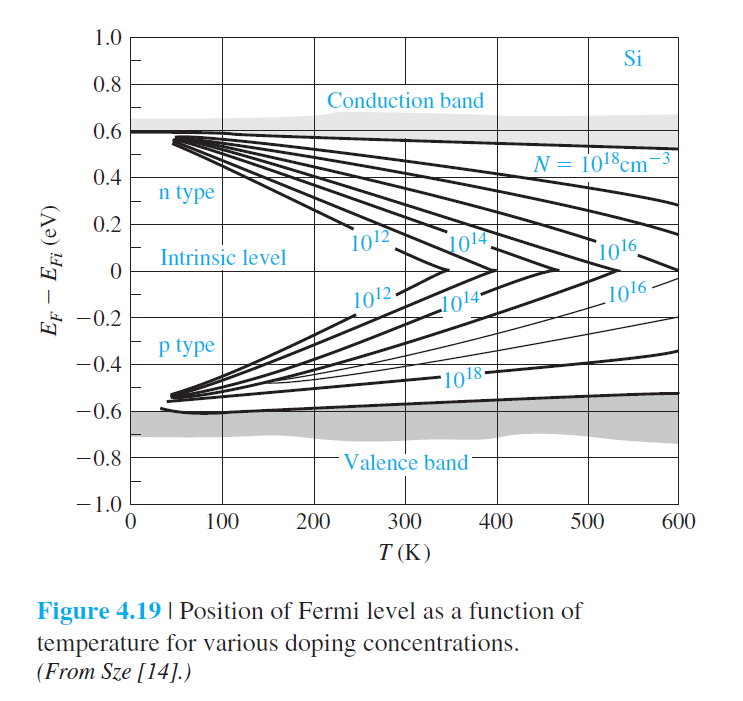
그림 4.19: 온도에 따른 $E_F-E_{Fi}$
온도가 증가할수록 $E_F$는 $E_{Fi}$에 접근. Extrinsic 특성을 잃고, intrinsic 특성을 갖는다.
Freeze-out이 발생하는 극저온에서는 Boltzmann근사가 적합하지 않고,
n-type에서는 $E_F > E_d$, p-type에서는 $E_F < E_a$
$T = 0$ K에서 $E_F$ 아래 모든 에너지 준위는 채워지고, $E_F$ 위의 모든 에너지 준위는 비게 된다.
4.6.3 Fermi Energy의 관련성
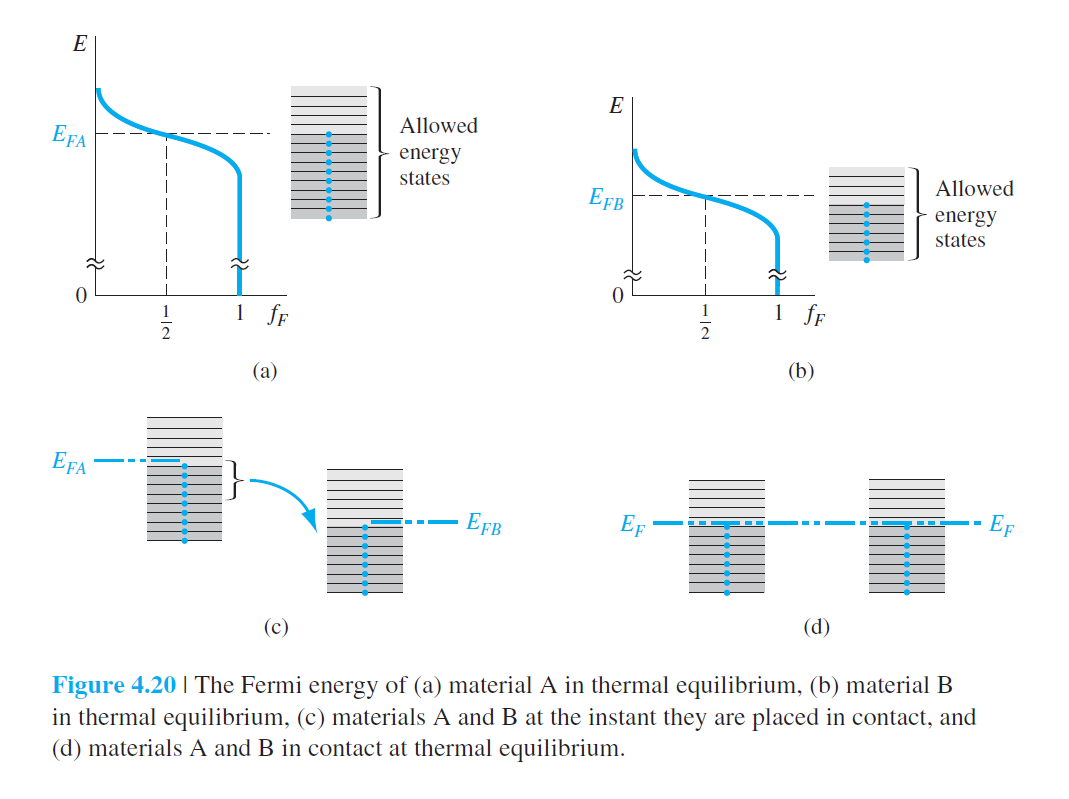
$E_F$가 다른 두 물질이 접촉을 했을 때, 전자들이 열평형을 이룰때까지 낮은 에너지로 이동.
두 물질에서 $E_F$가 같아짐.
