4. 유전체(Dielectric)
4.1 분극(polarization)
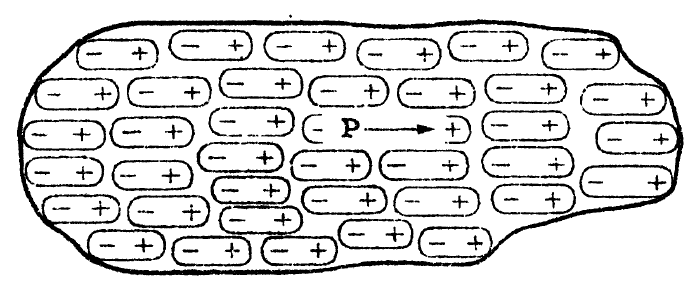
유전체에서 아주 작은 영역의 부피를 $\Delta V$라고 하고, 거기에 해당하는 전하량을 $dq$라고 하자.
이 부피에 해당하는 전기쌍극자 모먼트($\Delta \vec{p}$)는 다음과 같다.
$$
\Delta \vec{p}=\int_{\Delta v} \vec{r} d q
$$
이것을 $\Delta v$로 나눠준 값을 전기 분극(electric polarization) $\vec{P}$ 이라고 한다.
$$
\vec{P}=\frac{\Delta \vec{p}}{\Delta v} \quad\quad\quad \mathrm{C/m^2}
$$
전기 분극은 부피로 나눠준 값이기 때문에 유전체의 크기가 아닌 물질 자체의 특성으로 받아들일 수 있다.
만약에 $\Delta v$ 안에 여러분자가 있고 각 분자의 전기 쌍극자 모먼트가 다음과 같이 주어진다면,
\begin{equation}
\vec{p}_m=\int_{\textrm {분자}} \vec{r} d q
\end{equation}
전기 분극은 다음과 같이 기술될수도 있다.
\begin{equation}
\vec{P}=\frac{1}{\Delta v} \sum_m \vec{p}_m
\end{equation}
4.2 유전체 외부의 전기장
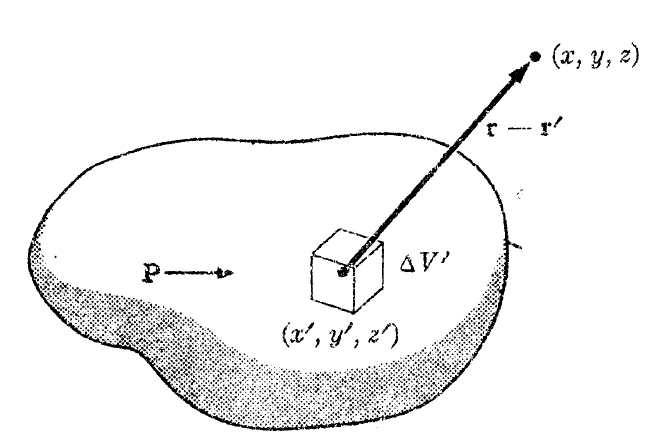
부피 $V_0$, 면 $S_0$로 정의되는 유전체 외부의 전기장을 구해보자.
먼저 전기쌍극자 모먼트에 의한 전기 포텐셜은 다음과 같이 주어진다는 것을 이미 배웠다.
$$
\Delta \varphi(\vec{r})=\frac{\Delta \vec{p} \cdot\left(\vec{r}-\vec{r}^{\prime}\right)}{4 \pi \epsilon_0\left|\vec{r}-\vec{r}^{\prime}\right|^3}=\frac{\vec{P}\left(\vec{r}^{\prime}\right) \cdot\left(\vec{r}-\vec{r}^{\prime}\right) \Delta v^{\prime}}{4 \pi \epsilon_0\left|\vec{r}-\vec{r}^{\prime}\right|^3}
$$
$$
\left|\vec{r}-\vec{r}^{\prime}\right|=\sqrt{\left(x-x^{\prime}\right)^2+\left(y-y^{\prime}\right)^2+\left(z-z^{\prime}\right)^2}
$$
유전체의 모든 부분에 의한 위치 $\vec{r}$에서의 포텐셜은 다음과 같이 적분으로 나타난다.
$$
\varphi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \int_{V_0} \frac{\vec{P}\left(\vec{r}^{\prime}\right) \cdot\left(\vec{r}-\vec{r}^{\prime}\right) d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}
$$
다음 사실들을 이용하면
$$
\nabla^{\prime}\left(\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right)=+\frac{\vec{r}-\vec{r}^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3},
$$
$$
\frac{\vec{P} \cdot\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}=\vec{P} \cdot \nabla^{\prime}\left(\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right)
$$
$$
\nabla^{\prime} \cdot(f \vec{F})=f \nabla^{\prime} \cdot \vec{F}+\vec{F} \cdot \nabla^{\prime} f,
$$
$$
\frac{\vec{P} \cdot\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}=\nabla^{\prime} \cdot\left(\frac{\vec{P}}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right)-\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|} \nabla^{\prime} \cdot \vec{P}
$$
적분은 다음과 같이 된다.
\begin{equation}
\varphi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \oint_{s_0} \frac{\vec{P} \cdot \hat{n} d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\frac{1}{4 \pi \epsilon_0} \int_{V_0} \frac{\left(-\nabla^{\prime} \cdot \vec{P}\right) d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}
\end{equation}
여기서 다음과 같이 정의되는 면전하밀도와 부피전하밀도를 이용하면,
$$
\begin{aligned}
& \sigma_P \equiv \vec{P} \cdot \hat{n} = P_n, \\
& \rho_{\vec{P}} \equiv-\nabla \cdot \vec{P},
\end{aligned}
$$
포텐셜은 다음과 같이 된다.
$$
\begin{aligned}
\varphi(\vec{r}) & =\frac{1}{4 \pi \epsilon_0}\left[\oint_{S_0} \frac{\sigma_P d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\int_{V_0} \frac{\rho_P d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right] \\
& =\frac{1}{4 \pi \epsilon_0} \int \frac{d q_P^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|},
\end{aligned}
$$
유전체에 유도된 전하는 다음과 같이 주어진다고 볼 수 있다.
$$
Q_P=\int_{V_0}\left(-\nabla^{\prime} \cdot \vec{P}\right) d v^{\prime}+\oint_{S_0} \vec{P} \cdot \hat{n} d a^{\prime}
$$
전기장은 다음과 같이 주어진다.
$$
\vec{E}(\vec{r})=\frac{1}{4 \pi \epsilon_0}\left[\int_{S_0} \frac{\sigma_P\left(\vec{r}-\vec{r}^{\prime}\right) d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}+\int_{V_0} \frac{\rho_P\left(\vec{r}-\vec{r}^{\prime}\right) d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right]
$$
4.3 유전체 내부의 전기장
유전체 내부의 전기장 표현은 외부에서 얻은 표현과 사실상 같다. \begin{aligned} \varphi(\vec{r})&=\frac{1}{4 \pi \epsilon_0} \int_{V_0-v_1} \frac{\rho_P\left(x^{\prime}, y^{\prime}, z^{\prime}\right) d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}\\ &+\frac{1}{4 \pi \epsilon_0} \int_{s_0+s^{\prime}} \frac{\sigma_P\left(x^{\prime}, y^{\prime}, z^{\prime}\right) d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|} \end{aligned}
4.4 유전체에서의 Gauss 법칙
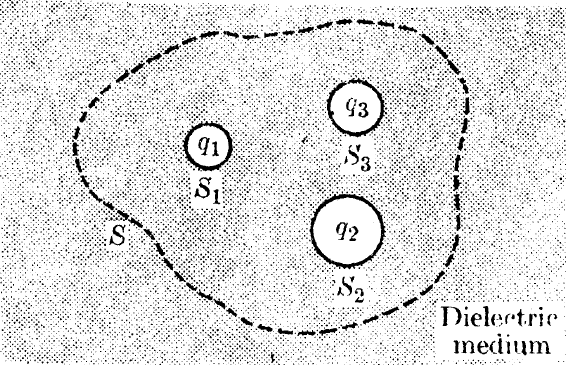
유전체 매질에 묻혀있는 $q_1$, $q_2$, $q_3$으로 대전된 세개의 도체들을 생각하자.
앞으로는 유전체와 섞여있는 실제 전하들은 유전체의 유도전하와 구분하기 위하여 외부전하라고 부를 것이다.
이 세 전하를 둘러싼 폐곡면(가우스면) $S$를 생각해 보자.
가우스 법칙을 고려하면 다음 식이 성립할 것이다.
\begin{equation}
\oint_S \vec{E} \cdot \hat{n} d a=\frac{1}{\epsilon_0}\left(Q+Q_P\right),
\end{equation}
위 식에서 $Q$와 $Q_P$는 다음과 같이 주어진다.
$$
Q=q_1+q_2+q_3
$$
$$
Q_P=\int_{S_1+S_2+S_3} \vec{P} \cdot \hat{n} d a+\int_V(-\nabla \cdot \vec{P}) d v
$$
위 식에서 부피 $V$는 표면 $S$와 각 도체의 표면 $S_1$, $S_2$, $S_3$ 사이의 공간의 부피이다.
위 식 우변의 두번째 항을 divergence 정리로 면적분으로 바꾸면, 면적분은 $S_1$, $S_2$, $S_3$, $S$의 면에 대해 행해지므로
$S_1$, $S_2$, $S_3$ 면에 대해 행해진 면적분은 위 식 우변의 첫번째 항과 상쇄되어 결국 다음과 같이 된다.
$$
Q_P=-\oint_S \vec{P} \cdot \hat{n} d a
$$
가우스 법칙에서 위 $Q_P$를 좌변으로 넘기면 다음 식이 얻어진다.
$$
\oint_S\left(\epsilon_0 \vec{E}+\vec{P}\right) \cdot \hat{n} d a=Q .
$$
위 식에서 다음의 electric displacement $\vec{D}$를 정의하면
$$
\vec{D}=\epsilon_0 \vec{E}+\vec{P}
$$
다음의 식이 얻어진다.
$$
\oint_S \vec{D} \cdot \hat{n} d a=Q
$$
위 식 또한 가우스 법칙이라고 한다.
위 식을 관찰해보면 유전체 내에는 외부전하와 유전체 내의 유도전하가 삮여 있지만,
$\vec{D}$장(field)은 외부전하만을 반영하고 있다는 것을 알 수 있다.
위 식의 미분형은 다음과 같이 주어진다.
$$
\oint_S \vec{D} \cdot \hat{n} d a=\rho \Delta V .
$$
$$
\nabla \cdot \vec{D}=\rho,
$$
전기장은 아래와 같이 외부전하에 의한 $\vec{D}$와 유전체내에 생성된 $\vec{P}$를 합한 효과로 나타나게 된다.
$$
\vec{E}(x, y, z)=\frac{1}{\epsilon_0} \vec{D}(x, y, z)-\frac{1}{\epsilon_0} \vec{P}(x, y, z),
$$
4.5 전기감수율(electric susceptibility)과 유전상수(electric constant)
유전체에 전기장을 가했을 때 $\vec{P}$가 얼마나 강하게 나타나는지를 표시하는 양인 electric susceptibility $\chi$를 다음과 같이 정의할 수 있다.
$$
\vec{P}=\chi(E) \vec{E}
$$
일반적으로 $\chi$는 전기장에 의존하는 양이다.
위 식과 $\vec{D}$의 정의를 겹합하면 다음을 얻는다.
$$
\begin{aligned}
\vec{D} & =\epsilon_0 \vec{E} + \chi(E) \vec{E}, \\
\vec{D} & =\epsilon(E) \vec{E}
\end{aligned}
$$
$\epsilon(E)$도 일반적으로 전기장에 의존하는 양이다.
그럼 위 식에서 $\epsilon(E)$는 다음과 같다.
$$
\begin{aligned}
\epsilon(E) =\epsilon_0+\chi(E)
\end{aligned}
$$
상황을 단순화하기 위해 $\chi$와 $\epsilon$가 전기장에 무관한 양이라고 가정하면 다음과 같이 쓸수 있다.
$$
\begin{aligned}
& \vec{P}=\chi \vec{E}, \\
& \vec{D}=\epsilon \vec{E}
\end{aligned}
$$
여기서 다음과 같이 정의되는 유전상수 $K$를 정의하자.
$$
\epsilon=K \epsilon_0
$$
그러면 $K$와 $\chi$ 사이의 관계는 다음과 같다.
\begin{equation}
K=\frac{\epsilon}{\epsilon_0} = 1+\frac{\chi}{\epsilon_0}
\end{equation}
좀더 정리하면 $\chi$는 진공의 유전율에 대한 차이이고,
$K$는 진공의 유전율에 대한 비율이다.
$$
\begin{aligned}
& \chi=\epsilon - \epsilon_0 \\
& K =\frac{\epsilon}{\epsilon_0}
\end{aligned}
$$
4.6 유전체내의 점전하
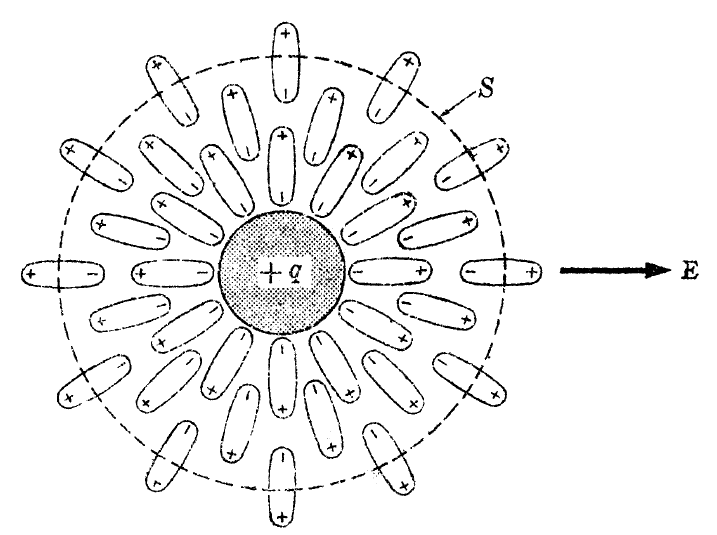
유전체내에 묻혀있는 점전하가 유전체내에 생성하는 전기장이 진공에서 얼마나 다른지 그 이유는 무엇인지 생각해 보자.
그림과 같은 유전체 내에 점전하 주위에 구대칭의 가우스면을 설정하여, 가우스 법칙을 적용하면 다음을 얻는다.
$$
\begin{aligned}
4 \pi r^2 D & =q \\
D & =\frac{q}{4 \pi r^2}, \\
\vec{D} & =\frac{q}{4 \pi r^3} \vec{r}
\end{aligned}
$$
$\vec{D}$장은 위와 같이 얻어지고, 전기장과 전기분극은 다음과 같이 주어진다.
$$
\begin{aligned}
& \vec{E}=\frac{q}{4 \pi K \epsilon_0 r^3} \vec{r} \\
& \vec{P}=\frac{(K-1) q}{4 \pi K r^3} \vec{r}
\end{aligned}
$$
위 식에서 보는 바와 같이, 전기장은 진공에서 보다 $K$만큼 적게 나타나게 된다.
위 전기장 식으로 보더라도 점전하는 $q$가 아닌 $q/K$만큼 줄어드는 효과가 나타남을 알수있지만,
$Q_P$를 계산해보더라도 그러한 사실을 다음과 같이 알수있다.
$$
Q_P=\lim _{b \rightarrow 0} 4 \pi b^2(\vec{P} \cdot \hat{n})_{r=b}=-\frac{(K-1) q}{K}
$$
$$
Q_P+q=\frac{1}{K} q,
$$
위와 같이 가우스면 내의 총전하는 $q$가 아닌 $q/K$로 축소된 효과로 전기장이 나타남을 알수있다.
이러한 현상의 이유는 가운데 점전하 때문에 그 주위에 유도된 유전체 내의 음의 표면 전하들이 생성되는데,
이 전하들 때문에, 가운데 양의 전하의 효과가 반감되는 효과가 발생하기 때문이다.
4.7 경계조건
매질이 달라질때 $\vec{E}$와 $\vec{D}$가지는 경계조건에 대해서 알아보자.
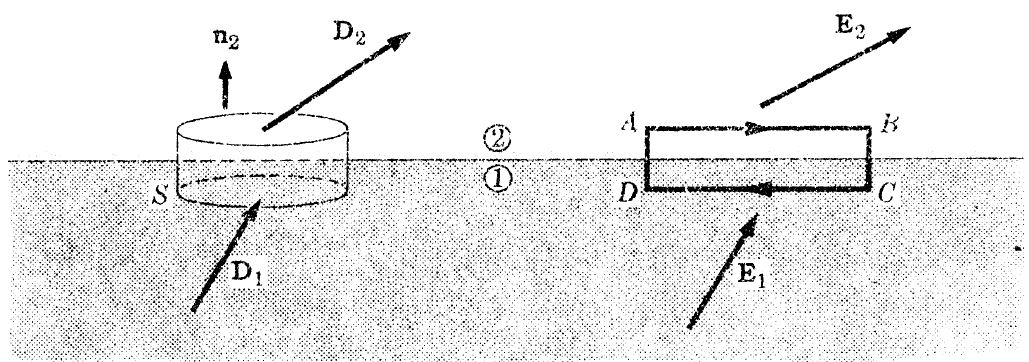
그림에서 보는 바와 같이 경계 주변에 경계면과 거의 붙은 가우스면을 설정하여, 가우스 법칙을 적용하자.
가우스면 내에 존재하는 전하는 다음과 같은데, 가우스면내의 부피가 거의 0이라서 부피 전하밀도들은 거의 0으로 취급한다.
$$
\sigma \Delta S+\frac{1}{2}\left(\rho_1+\rho_2\right) \times \text { volume }
$$
그러면 다음과 같은 결과를 얻는다.
$$
\vec{D}_2 \cdot \hat{n}_2 \Delta S+\vec{D}_1 \cdot \hat{n}_1 \Delta S=\sigma \Delta S
$$
$$
\left(\vec{D}_2-\vec{D}_1\right) \cdot \hat{n}_2=\sigma
$$
$\vec{D}$ 장에 대한 경계조건은 다음과 같다. 즉
$$
D_{2 n}-D_{1 n}=\sigma
$$
즉 $\vec{D}$ 장은 경계의 수직 성분이 연속이다.
경계 주위에 경계와 거의 붙은 경로를 설정하고 이 경로에 대해 전기장에 대한 경로적분을 시행하면 다음과 같다.
$$
\vec{E}_2 \cdot \Delta \vec{l}+\vec{E}_1 \cdot(-\Delta \vec{l})=0,
$$
$$
\left(\vec{E}_2-\vec{E}_1\right) \cdot \Delta \vec{l}=0
$$
$$
E_{2 t}=E_{1 t}
$$
즉 $\vec{E}$ 장은 경계의 수평 성분이 연속이다.
포텐셜의 경계조건
포텐셜은 경계에서 연속이다. 이것은 다음 식에서 이해할 수 있다.
$$ \Delta \varphi = - \int_1^2 \vec{E} \cdot d \vec{r}$$
위 식은 경계를 가로지르는 경로 적분인데, 두 지점 1과 2는 다른 매질에 있다.
만약 두 지점 1과 2가 극한으로 매우 가깝게 위치 있다면, 위 식의 우변은 0이 될것이다.
그러면 좌변은 $\varphi_2-\varphi_1=0$이 되어, 결과적으로 다음을 얻는다.
$$\varphi_2=\varphi_1$$
이것은 포텐셜이 경계에서 연속이라는 것을 의미한다.
만약에 도체와 경계인 경우 전기장과 D 장은 다음의 관계를 가진다.
\begin{equation}
E_{2 t}=0
\end{equation}
도체 표면에서 나오는 전기장이 왜 도체면에 수직인지 여기서 알 수 있다.
\begin{equation}
D_{2 n}=\sigma
\end{equation}
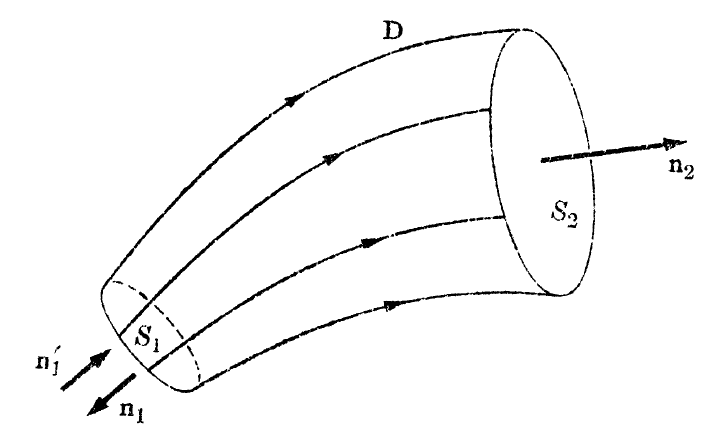
그림과 같이 D장에 나란한 방향으로 설정된 튜브형 가우스면을 생각하면,
튜브의 양끝단을 통과하는 D다발의 차이가 그 튜브내의 외부 전하량과 같다는 것을 알수있다.
\begin{equation}
\int_{S_2} \vec{D} \cdot \hat{n} d a-\int_{S_1} \vec{D} \cdot \hat{n}^{\prime} d a=Q
\end{equation}
4.8 유전체를 포함한 Laplace방정식의 풀이
이 장에서 유전체 매질이 존재하는 경우 가우스법칙의 미분형은 다음과 같이 주어진다는 것을 배웠다.
$$
\nabla \cdot \vec{D}=\rho
$$
만약 유전체가 선형성, 등방성, 균일성 물질이면
$\vec{D}=\epsilon \vec{E}$이 성립한다.
그러면 다음이 성립한다.
$$
\nabla \cdot \vec{E}=\frac{1}{\epsilon} \rho
$$
다음의 전기장과 포텐셜의 관계를 생각하면
$$
\vec{E}=-\nabla \varphi
$$
다음의 Poisson 방정식이 다시 성립한다.
$$
\nabla^2 \varphi=-\frac{1}{\epsilon} \rho
$$
위 식이 진공일 경우와의 차이점은 $\epsilon_0$ 가 아닌 $\epsilon$로 대체되었다는 것이다.
주의할 것은 $\rho$는 총전하 밀도가 아닌 외부전하 밀도라는 것이다.
유전체내의 전기장을 구하고자하면 $\rho=0$이 되는 다음 Laplace방정식을 이용하면 된다.
$$
\nabla^2 \varphi=0
$$
왜냐하면 이미 언급한대로 위에 적혀있는 Poisson방정식의 우변에 $\rho$는 외부전하이기 때문에
유전체내에서는 유도전하가 존재하는 것이지 외부전하는 애초에 존재하지 않기 때문이다.
(예제)
일정한 전기장 내에 유전체 구
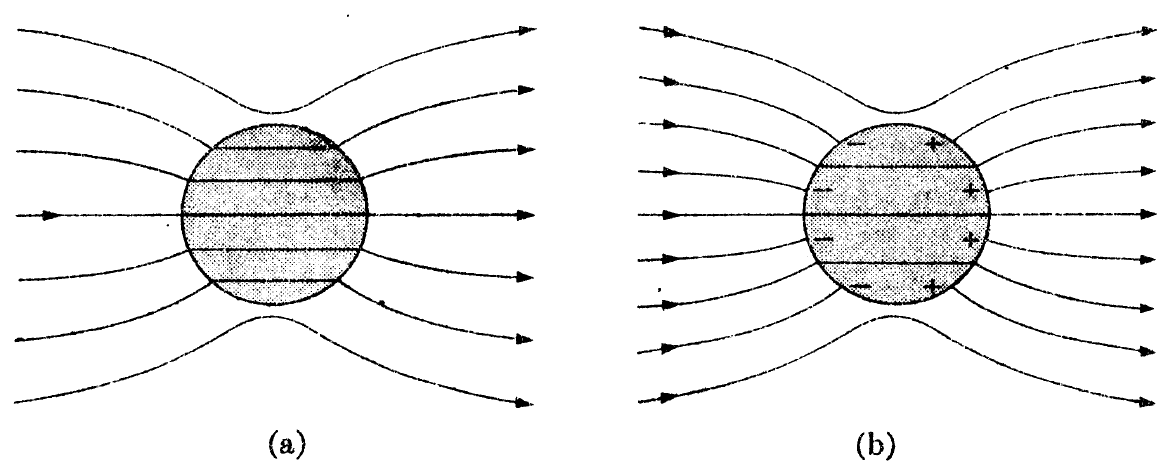
경계조건1: 무한대에서 ($r \rightarrow \infty$) 전기장이 $E_0 \hat{k}$
$$
\begin{aligned}
{[\vec{E}(r, \theta)]_{r \rightarrow \infty} } & =\vec{E}_0=E_0 \hat{k} \\
{[\varphi(r, \theta)]_{r \rightarrow \infty} } & =-E_0 z+\text { 상수 } \\
& =-E_0 r \cos \theta+\text { 상수 }
\end{aligned}
$$
3장에서처럼 다음의 해를 선택하자. 1은 유전체 외부를 2는 유전체 내부를 의미한다.
외부전하는 없으므로 $1/r$항은 제외된다.
$$
\varphi_1(r, \theta)=A_1 r \cos \theta+C_1 r^{-2} \cos \theta
$$
$$
\varphi_2(r, \theta)=A_2 r \cos \theta+C_2 r^{-2} \cos \theta
$$
$r\rightarrow \infty$에서 포텐셜은 $-E_0 r \cos \theta$이므로, 우선 $A_1=-E_0$임을 알 수 있다.
유전체 내부에서 중심($r=0$)에서는 $r^{-2}$ 이 항이 발산하므로,
$\varphi_2(r, \theta)$의 두번째 항은 제거한다.
경계 조건2: $D_{1n} = D_{2n}$을 적용하면,
$$\epsilon_1 \left. \frac{\partial \varphi_1}{\partial r}\right|_{r=a} = \epsilon_2 \left. \frac{\partial \varphi_2}{\partial r}\right|_{r=a}$$
$$\epsilon_1 (-E_0 \cos \theta-2 C_1 a^{-3} \cos \theta) = \epsilon_2 A_2 \cos \theta $$
$$E_0+2 C_1 a^{-3} = - K A_2 $$
경계 조건3: $E_{1t} = E_{2t}$을 적용하면,
$$\left. \frac{1}{r} \frac{\partial \varphi_1}{\partial \theta}\right|_{r=a} = \left. \frac{1}{r}\frac{\partial \varphi_2}{\partial \theta}\right|_{r=a}$$
$$ E_0 \sin \theta - C_1 a^{-3} \sin \theta = - A_2 \sin \theta $$
$$ E_0 - C_1 a^{-3} = - A_2 $$
위 조건은 포텐셜 연속 조건 $\varphi_1=\varphi_2$으로도 얻어진다.
위 식들로부터 다음이 얻어진다.
$$
A_2=-\frac{3 E_0}{K+2}
$$
$$
C_1=\frac{(K-1) a^3 E_0}{K+2}
$$
$$
\vec{E}_2=\frac{3}{K+2} \vec{E}_0
$$
유전체 구내의 전기장은 $z$ 방향으로 나란하게 주어짐을 알수있다.
4.9 영상전하법
유전체가 존재하는 경우 영상전하법을 이용하여 풀어보자.
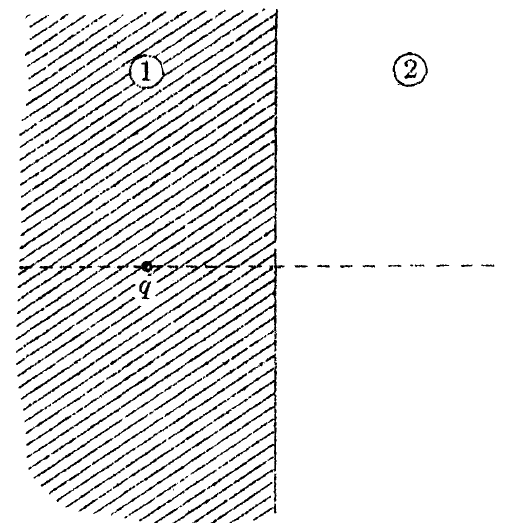
위 그림과 같이 반무한 유전 매질속에
외부 전하 $q$가 유전체 표면에서 거리 $d$만큼 떨어진 유전체 매질내에 박혀있다.
위 그림에서 가로 방향을 $x$축이라고 하자.
3장에서 처럼 경계조건 $D_{1n}=D_{2n}$과 $E_{1t}=E_{2t}$을 만족하는 영상전하들을 구해보자.
매질1에서의 포텐셜은 다음과 같이 전하 $q$와 위치 $\vec{r}'$에 위치하는 영상전하 $q'$에 의한 포텐셜로 주어진다고 가정하고,
$$
\varphi_1=\frac{1}{4 \pi \epsilon_1}\left[\frac{q}{r}+\frac{q^{\prime}}{r^{\prime}}\right]
$$
매질2에서의 포텐셜은 다음과 같이 $q$의 위치에 있는 영상전하 $q''$에 의한 포텐셜로 주어진다고 가정하자.
$$
\varphi_2=\frac{q^{\prime \prime}}{4 \pi \epsilon_2 r}
$$
여기서 $r$과 $r'$은 다음과 같이 주어진다.
$$
r=\sqrt{(x+d)^2+y^2+z^2} \quad r^{\prime}=\sqrt{(x-d)^2+y^2+z^2}
$$
경계조건 $D_{1n}=D_{2n}$으로부터 다음을 얻는다.
$$
\frac{\left(q+q^{\prime}\right) y}{\epsilon_1\left[d^2+y^2+z^2\right]^{3 / 2}}=\frac{q^{\prime \prime} y}{\epsilon_2\left[d^2+y^2+z^2\right]^{3 / 2}}
$$
경계조건 $E_{1t}=E_{2t}$으로부터 다음을 얻는다.
$$
\frac{\left(q-q^{\prime}\right) d}{\left[d^2+y^2+z^2\right]^{3 / 2}}=\frac{q^{\prime \prime} d}{\left[d^2+y^2+z^2\right]^{3 / 2}}
$$
결과적으로 경계조건을 만족하는 영상전하들은 다음과 같이 주어진다.
$$
q^{\prime}=\frac{\epsilon_1-\epsilon_2}{\epsilon_1+\epsilon_2} q, \quad q^{\prime \prime}=\frac{2 \epsilon_2}{\epsilon_1+\epsilon_2} q
$$
4.10 유전체의 응용
$$
\vec{p}_m=\alpha \vec{E}_m
$$
$\alpha$ : polarizability
$$
\vec{P}=N \alpha\left(\vec{E}+\frac{1}{3 \epsilon_0} \vec{P}\right)
$$
Clausius-Mossotti 방정식
\begin{equation}
\alpha=\frac{3 \epsilon_0(K-1)}{N(K+2)}
\end{equation}
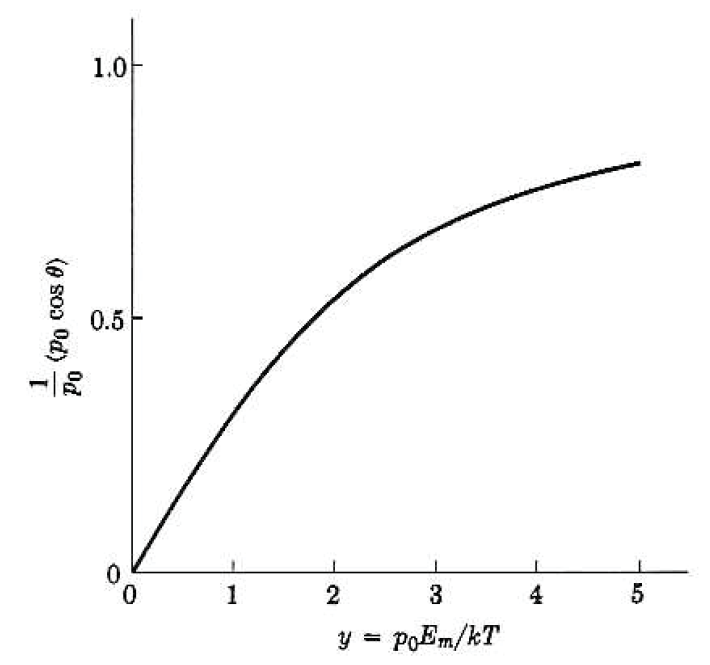
\begin{equation}
\alpha=\alpha_0+\frac{p_0^2}{3 k T}
\end{equation}
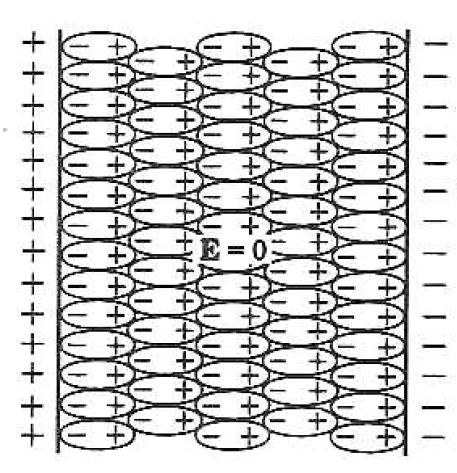
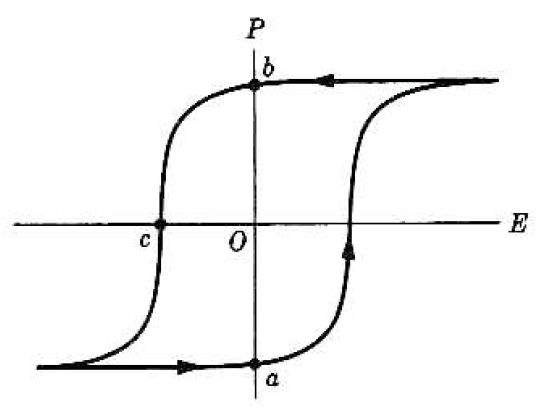
• 강유전체(Ferroelectric)

축전기, NAND flash memory, MOSFET
• 압전체(Piezoelectric)
가스라이터, 평판형 스피커