5. 수송현상
지금까지는 전자와 홀(hole)의 농도(concentration)을 계산해왔다.
이장에서는 이들이 이동하면서 발생하는 전류 값을 좀더 상세히 계산해본다.
이러한 전하들이 이동하는 현상을 transport 또는 수송현상이라고 한다.
이장에서는 표류(drift)와 확산(diffusion) 이 두 가지 수송 메카니즘을 공부한다.
표류는 전기장에 의한 것이고,
확산은 전하 농도차이에 의한 전하의 흐름이다.
이 장에서는 암묵적으로 열 평형 상태를 가정한다.
비 평형 상태는 다음장에서 다룬다.
5.1 운반자 표류(carrier drift)
5.1.1 표류 전류 밀도(drift current density)
전류의 정의 : 시간 $t$ 동안 면적 $A$를 통과하는 전하량
전류가 시간에 따라 일정할 경우. 시간 $t$동안 전하량 $q$ 통과
$$I=\frac{q}{t}$$
전류가 시간에 따라 일정하지 않는 일반적인 경우
$$I=\frac{dq}{dt}$$
$$dq = (v_d dt)(A) \rho $$
$\rho$ : 전하밀도 (Coul/cm$^3$)
$$ I=\frac{v_d dt A \rho}{dt} $$
전류 밀도의 : $J = I / A$
$$ J = \frac{I}{A} = \frac{v_d dt A \rho}{dt A} = \rho v_d$$
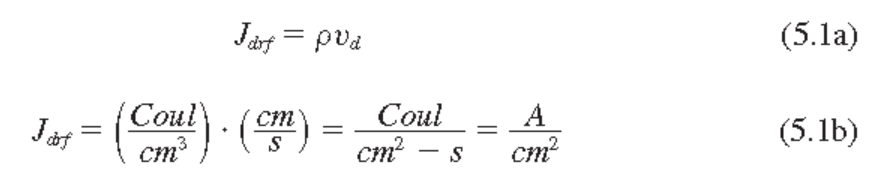
hole에 의한 drift current
전기장이 있는 상황에서 hole에 대한 운동방정식
$m_{cp}^*$ : hole의 conductivity effective mass(hole의 전도 유효질량)
뉴튼 법칙만 보면 속도가 지속 증가해야 하지만, 실제로는 전자가 결정내의 충돌로 인하여
결국 어떤 일정한 속도 $v_d$로 진행하게 된다.
$v_d$는 전기장 $E$에 비례하고, 비례계수를 mobility(이동도)라고 한다.
Mobility의 단위 : (cm/sec)/(V/cm) = (cm$^2$/sec)/V
(5.2)와 (5.4)로 부터
hole의 drift전류는 전기장과 같은 방향.
전자에 대해서 (5.6), (5.7), (5.8)식이 성립
전자의 속도는 전기장에 반대방향
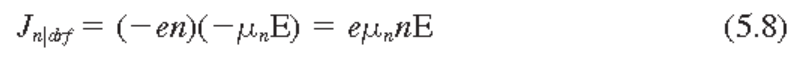
전자의 속도는 전기장에 반대방향이지만, 전류는 전기장과 같은 방향.
전자와 hole의 전류를 합친 총 drift 전류밀도.
hole에 대한 방정식
$v$는 전기장에 의한 속도. Random thermal velocity(무작위 열속도)는 제외.
시간 $t$후의 속도. $t=0$에서의 속도는 0이라고 가정.
$\tau_{cp}$
: relaxation time, collision 시간, mean free time
: 어떤 순간에 랜덤하게 선택된 전자가 다음 충돌까지 여행한 시간의 평균
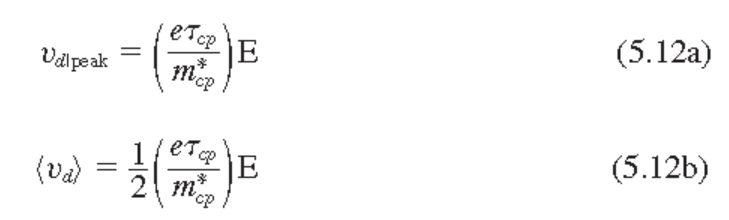
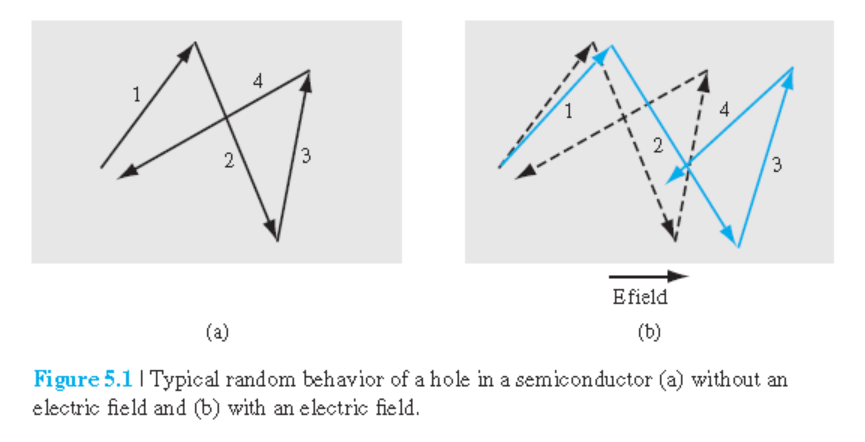
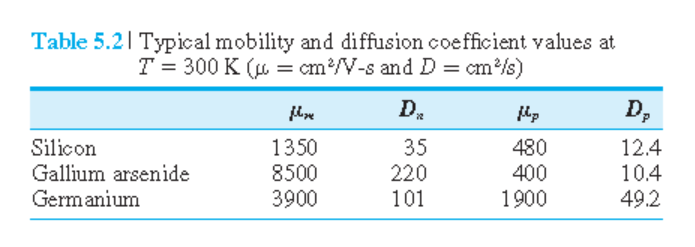
hole과 전자의 이동도
두 가지 scattering mechanism: phonon 산란(lattice scattering), ionized 불순물 산란.
1. phonon 산란
scattering 이론에 의하면 1차오더로 다음과 같이 주어진다.
약하게 doped된 반도체에서는 phonon 산란이 지배적이고,
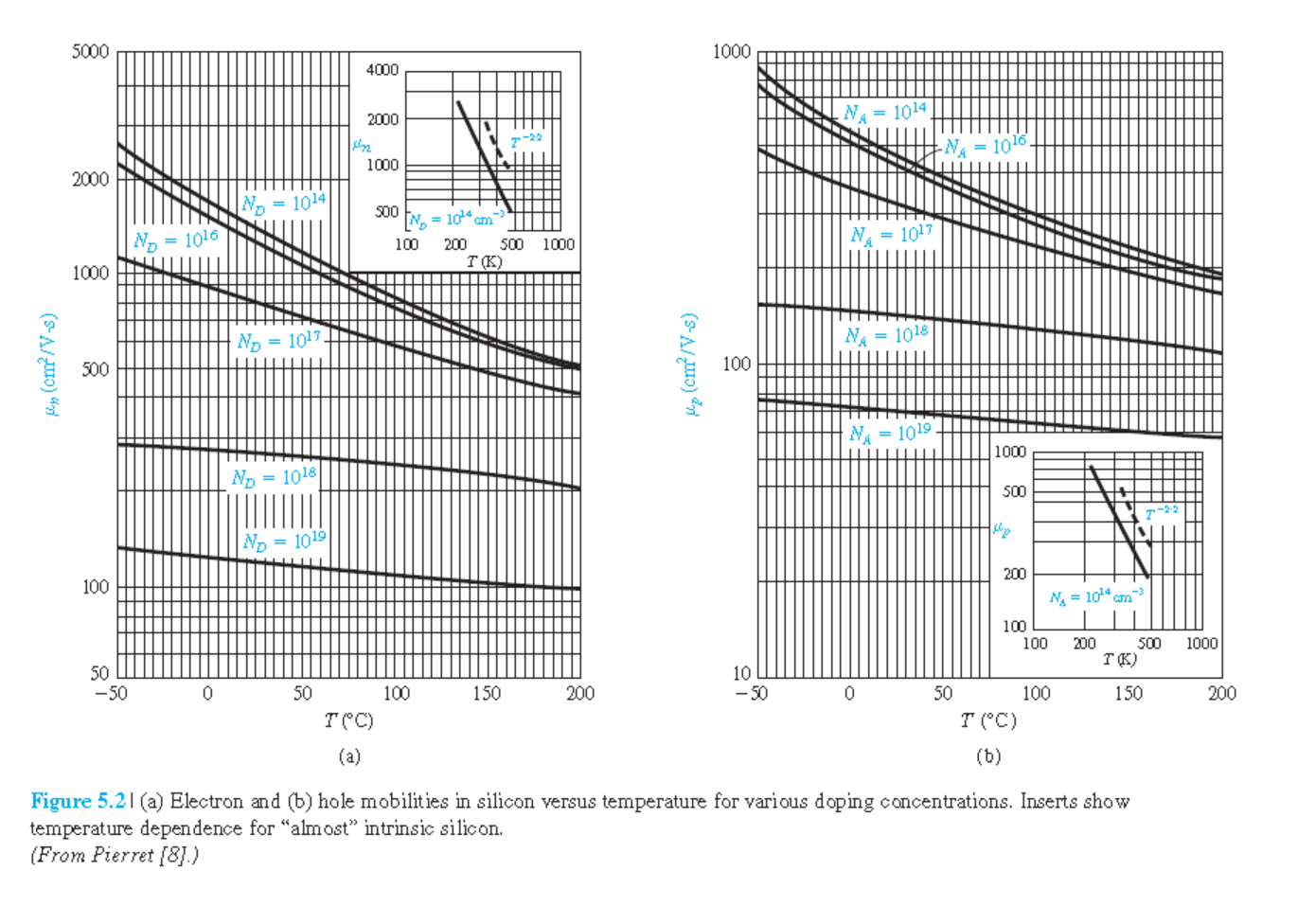
온도가 증가함에 따라서 mobility 감소. $\mu \sim T^{-n}$. 그림 5.2 참조
2. ionized 불순물 산란
carrier들이 ionized 불순물과 전기적 상호작용.
불순물 scattering만 있을 경우
$N_I = N_d^+ + N_a^-$ : 반도체의 총 이온화 불순물 농도.
온도에 따라 증가하는 이유 : random thermal velocity의 증가로 carrier가 불순물 중심 근처에 머무는 시간이 줄어듬.
격자산란과 불순물 산란 모두 존재. 독립적.
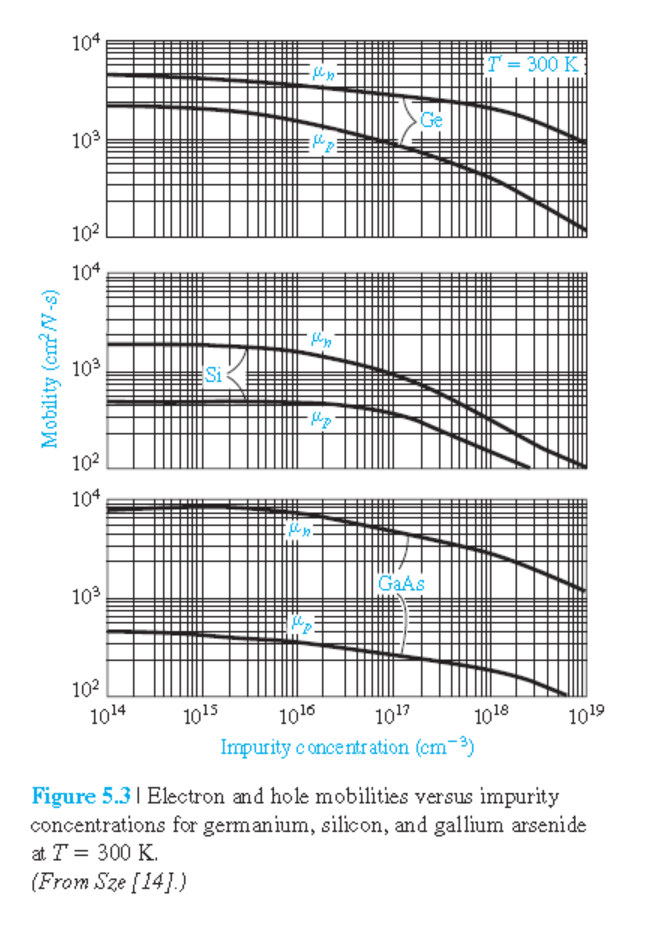
Mobility 표현.
• 전도도와 비저항
(5.9)식으로 부터
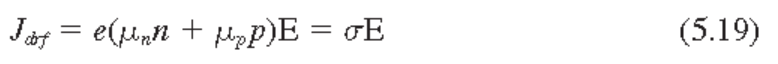
$\sigma$ : 반도체의 conductivity $(\Omega cm)^{-1}$.
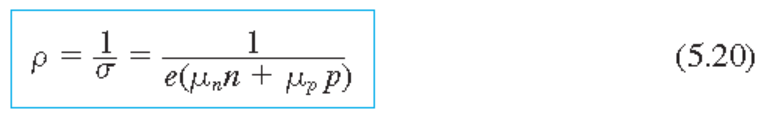
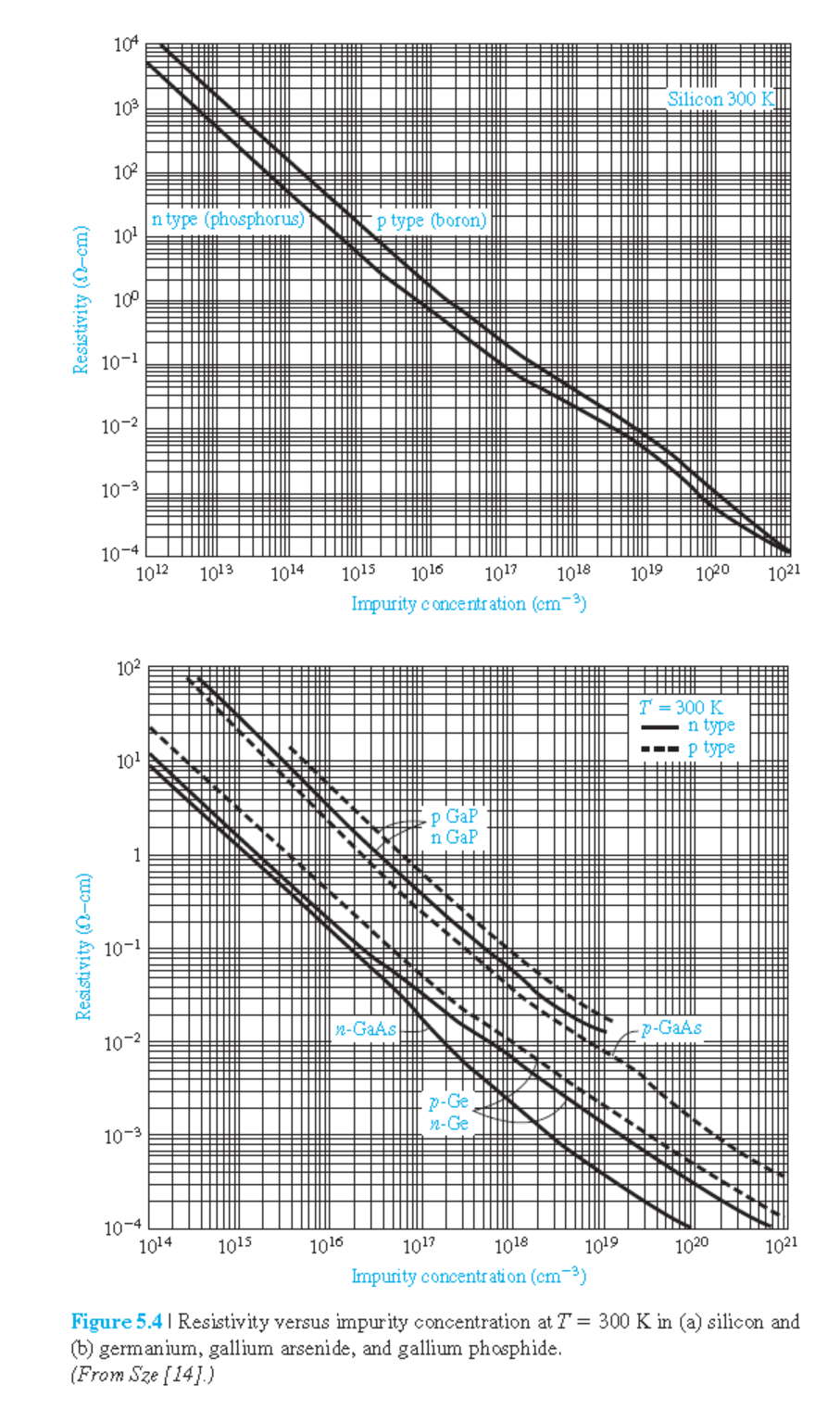
$\rho$ : 반도체의 resistivity(저항도, 비저항) $\Omega cm$.
그림 5.4 resistivity 참고.
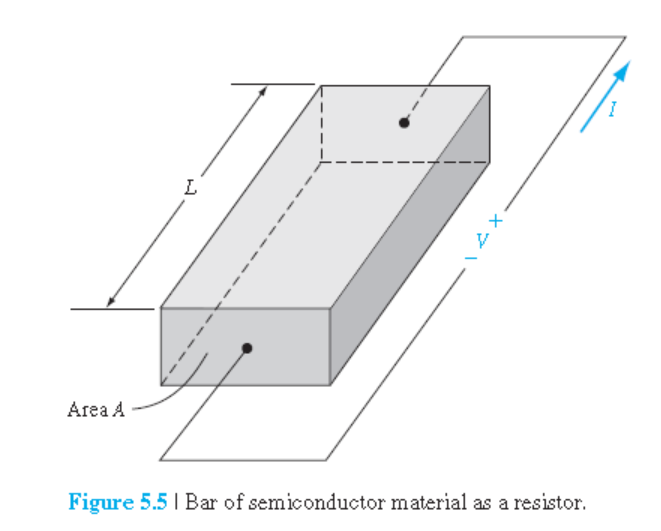
• Ohm의 법칙
\begin{equation}
\begin{aligned}
J &=\frac{I}{A} \qquad (5.21a) \\
E &=\frac{V}{L} \qquad (5.21b) \\
\frac{I}{A} &=\sigma\left(\frac{V}{L}\right) \qquad (5.22a) \\
V &=\left(\frac{L}{\sigma A}\right) I=\left(\frac{\rho L}{A}\right) I=I R \qquad (5.22a)
\end{aligned}
\end{equation}
p-type 반도체의 경우($N_a \gg n_i$, $N_d = 0$)
\begin{equation}
\begin{aligned}
\sigma &=e\left(\mu_n n+\mu_p p\right) \approx e \mu_p p \qquad (5.23) \\
\sigma &\approx e \mu_\rho N_a \approx \frac{1}{\rho} \qquad (5.24)
\end{aligned}
\end{equation}
• 완전 이온화
extrinsic 반도체의 전도도와 비저항은 주로 다수 운반자에 의한 기여이다.
• 그림 5.6은 $N_d = 10^{15}$ cm$^{-3}$인 Si에서 온도에 따른 전자의 농도와 전도도를 보여준다.
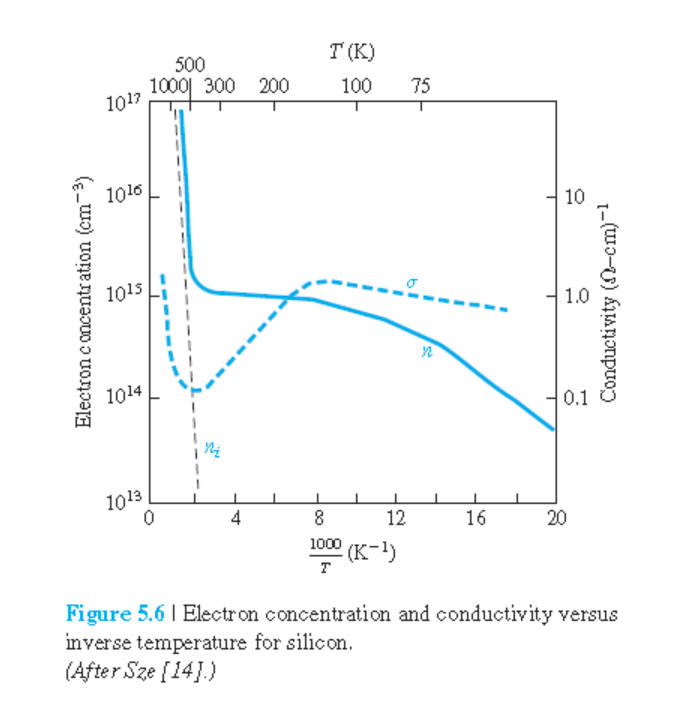
• intrinsic 반도체에서는 $p_0 = n_0 = n_i$이므로 전도도는 다음과 같이 주어진다.
\begin{equation}
\sigma_i=e\left(\mu_n+\mu_p\right) n_i \qquad (5.25)
\end{equation}
식 (5.4) $v_d = \mu E $에서 $\mu$가 상수면 전기장과 $v_d$ 비례
전기장이 높은 값에서는 $v_d$의 증가가 정체.
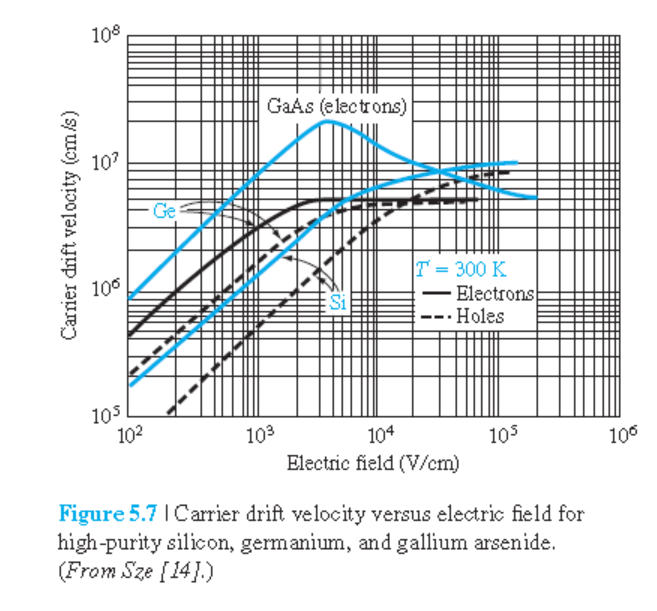
실리콘에서 실험적으로 얻어진 $drift$ 속도와 전기장과의 관계
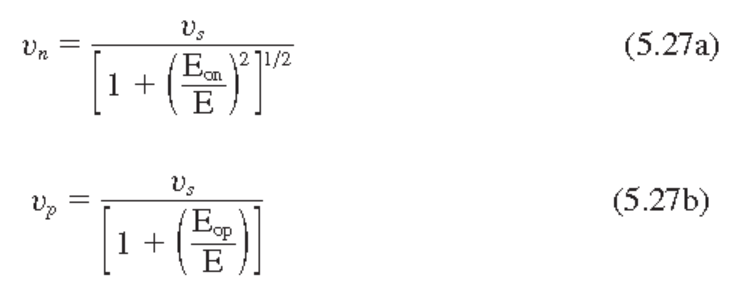
전기장이 낮을 때 : $drift$ 속도와 전기장은 선형성
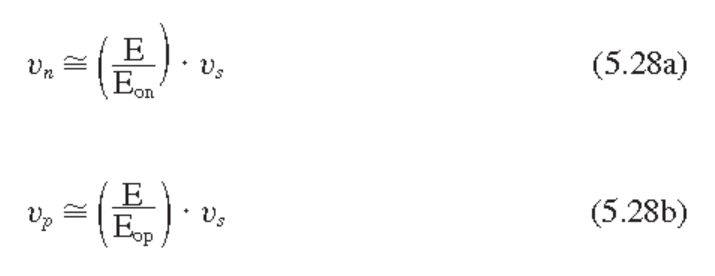
전기장이 높을 때는 속도 포화
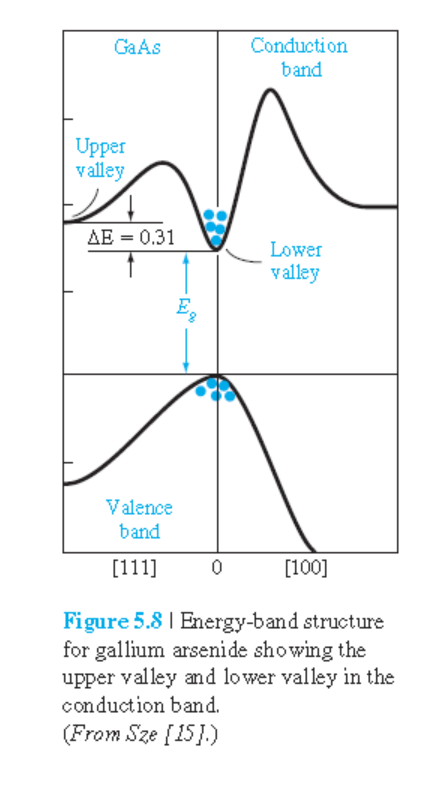
• GaAs의 경우 그림 5.7에서 고전기장에서 $v_d$가 감소에 대한 이유
아래 그림 5.8에서와 같이 적절한 전기장에서는 전자가 유효질량이 작은 lower valley에 존재하나
더욱 큰 전기장에서는 에너지는 더 높지만 유효질량이 더 큰 upper valley에 전자가 존재하기 때문.
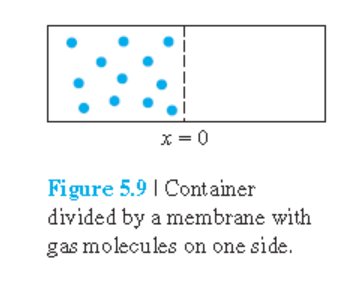5.2.1 Diffusion Current Density
Mean free path(평균 자유 경로) : $l(=v_{\mathrm{th}}\tau_{\mathrm{cn}})$
Net rate of electron flow(순 전자흐름률)
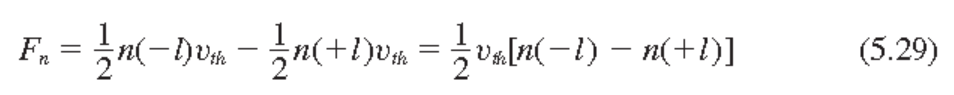
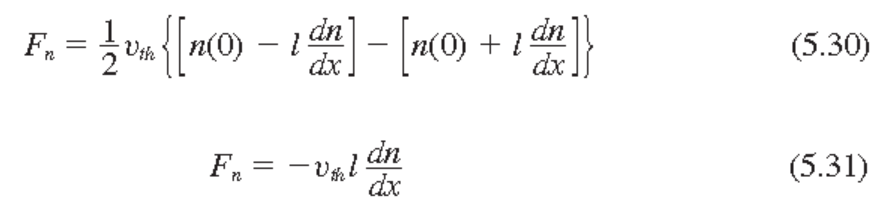
Taylor 전개
$$ f(x) = f(a) + \frac{f'(a)}{1!}(x-a)+ \frac{f''(a)}{2!}(x-a)^2 + \cdots $$
$$ f(x) = f(0) + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \cdots $$
Electron diffusion current density (전자 확산 전류 밀도)
$D_n$: electron diffusion coefficient(전자 확산 계수), cm$^2$/sec
$D_p$: hole diffusion coefficient(hole 확산 계수), cm$^2$/sec
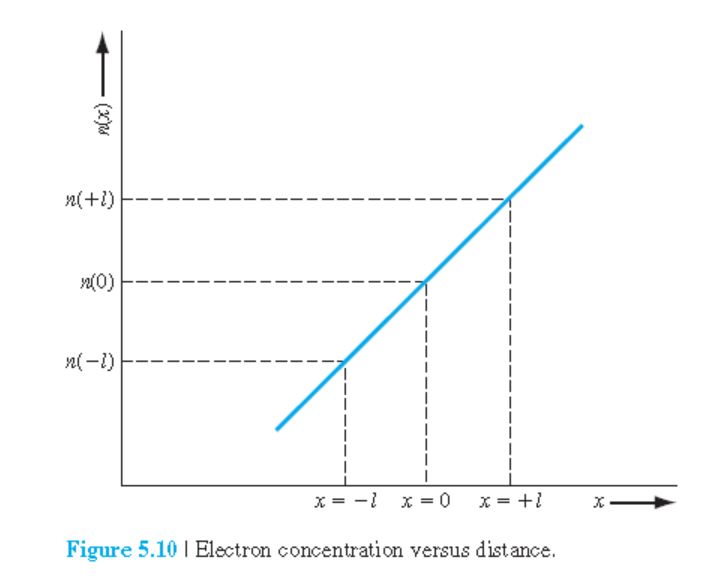
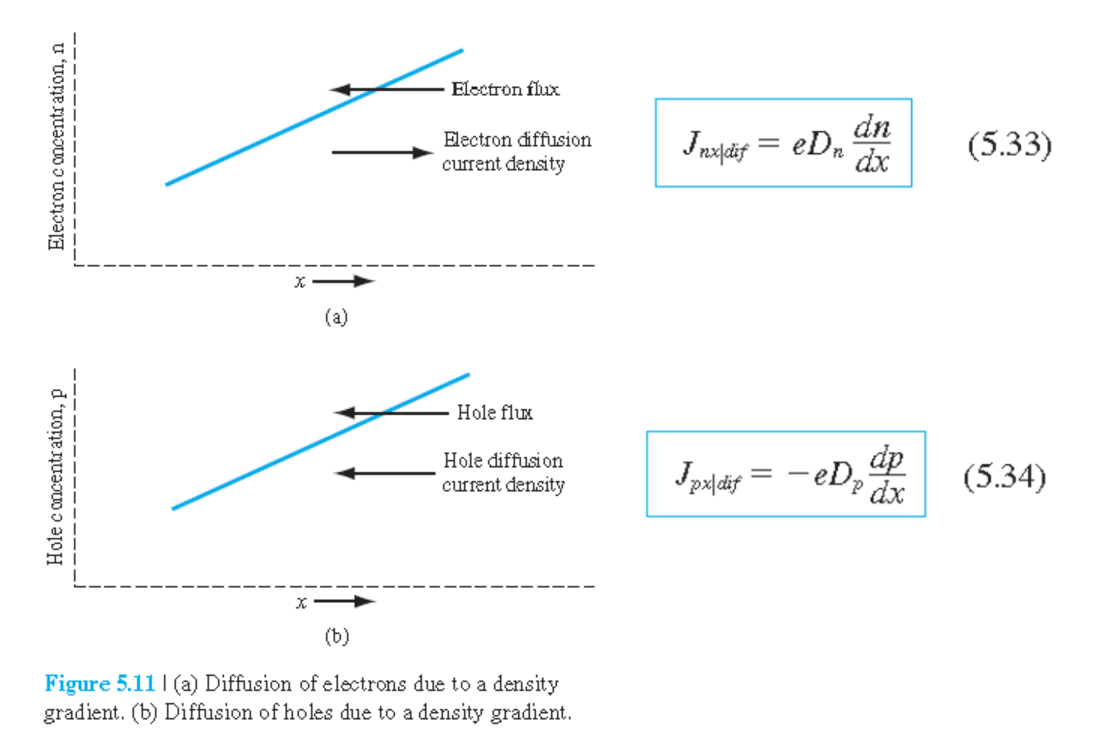
전자와 hole의 drift 및 diffusion은 모두 독립적. 이들 기여를 모두 합하여 전체 전류밀도를 구할 수 있다.
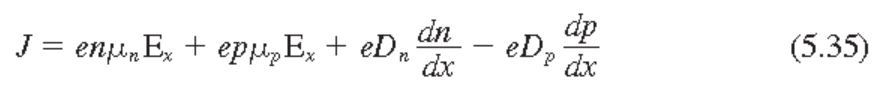
3차원으로의 일반화
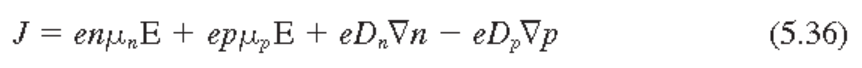$$ \vec{J} = e n\mu_n \vec{E} + e p\mu_p \vec{E} + e D_n \nabla n - e D_p \nabla p$$
5.3.1 유도 전기장
$x$가 증가할 수 록, donor 도핑이 선형적으로 감소하는 경우 (그림 5.12)
Electric potential $\phi$
전기장
완전 이온화 ($n_0 \approx N_d$)에서의 전기장
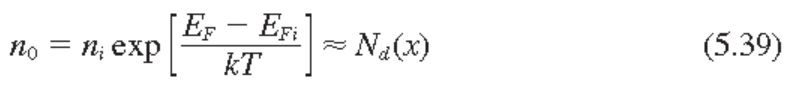
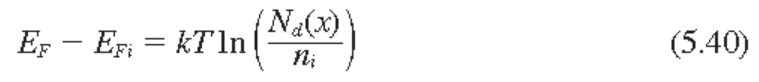
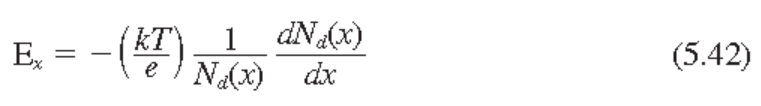
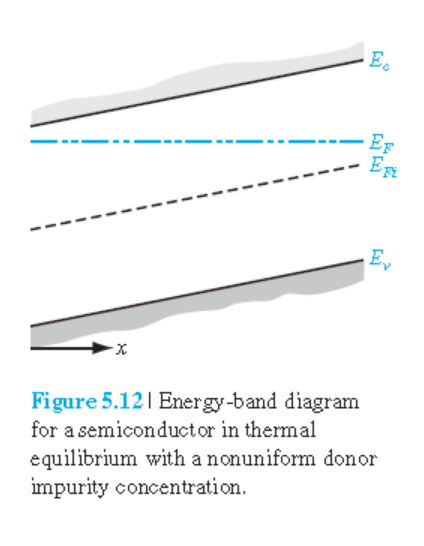
지금까지는 표류전류와 확산전류가 서로 무관한 것처럼 기술되었지만
이 절에서는 이 둘사이에는 관련이 있다는 것을 보여준다.
불균일 도핑된 열평형상태의 반도체에서 전자 및 hole의 전류는 0이다.
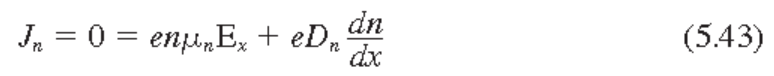
N형 반도체 완전 이온화 상태에서 quasi-중성 조건: $n_0 \approx N_d$
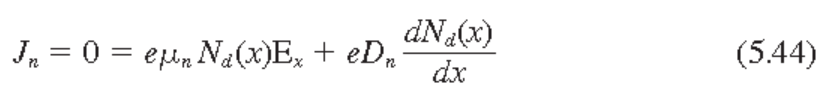
5.42식 이용하면 결과적으로
N형 반도체에서는 다음이 성립한다.
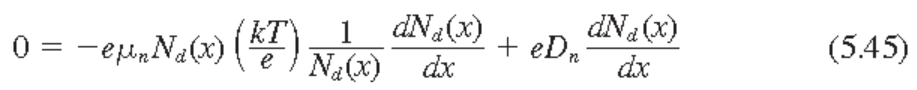P형 반도체에서는 다음이 성립한다.
종합하면 다음이 성립한다.
이것이 Einstein 관계식이며, 이전 절까지 무관하게 취급되었던,
이동도와 확산 계수사이의 관계를 mobility와 diffusion coefficient와의 관계
5.4 Hall 효과(The Hall effect)
• Hall 효과는 반도체가 $n$형인지 $p$형인지를 결정하고, 다수 운반자의 농도를 측정하는데 사용될 수 있다.
반도체에 전기장 $\vec{E}$와 자기장 $\vec{B}$가 가해질 때,
전하 $q$를 가지는 입자가 받는 힘은 다음과 같이 주어진다.
\begin{equation}
\vec{F}=q (\vec{E} + \vec{v} \times \vec{B}) \qquad (5.48)
\end{equation}
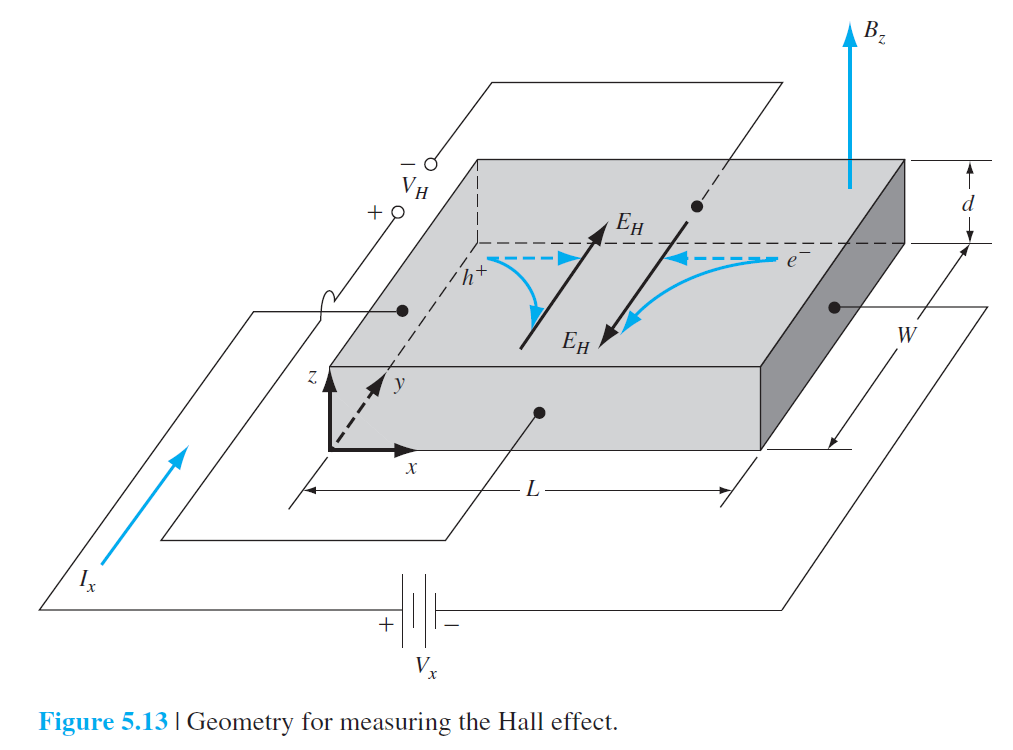
• 그림 5.13은 Hall 효과를 나타낸다.
위 그림에서 전기장은 $+x$방향으로, 자기장은 $+z$방향으로 걸려있다.
$p$형 반도체라면 양전하가 자기장에 힘을 받아 경로가 휘어지면서 $y = 0$인 면에 축적될 것이다.
그러면 그 반대편인 $y = W$인 면은 자연스럽게 음의 전하를 띄게 될 것이다.
이렇게 되면 $y = 0$과 $y = W$ 사이에는 전기장이 발생하게 된다.
이 전기장을 Hall 전기장($E_H$)이라고 부르며,
$y = 0$과 $y = W$ 사이에 걸리는 전압을 Hall 전압($V_H$)이라고 한다.
$$ V_H = + E_H W $$
정상상태에 도달하게 되면, $y = 0$인 면에 축적된 전자들에 가해지는 알짜힘의 $y$성분은 0이 된다.
(5.48)식의 $y$성분이 0이되면 다음을 얻는다.
$$ q E_y = q v_x B_z $$
여기서 $E_y$가 $E_H$에 해당한다.
그러면 Hall 전압은 다음과 같이 얻어진다.
$$ V_H = v_x W B_z \qquad (5.51)$$
위 식에서 $v_x$는 $x$방향으로의 표류 속력을 의미한다.
$v_x$는 다음과 같이 hole의 농도와 관련이 있다.
$$v_x = \frac{J_x}{e p}=\frac{I_x}{(e p)(W d)}$$
$V_H$는 다음과 같이 주어지고,
$$
V_H = \frac{I_x B_z}{e p d}
$$
hole 농도는 다음과 같이 주어진다.
$$ p = \frac{I_x B_z}{e d V_H} $$
• Mobility(이동도)는 다음과 같은 과정으로 주어질 수 있다.
$$
J_x = e p \mu_p E_x
$$
$$
\frac{I_x}{W d}=\frac{e p \mu_p V_x}{L}
$$
$$ \mu_p=\frac{I_x L}{e p V_x W d} $$
• $n$형 반도체에 대해서는 다음과 같이 주어진다.
$$ V_H = -\frac{I_x B_z}{n e d} \qquad (5.55) $$
$$ n = -\frac{I_x B_z}{e d V_H} \qquad (5.56) $$
$$ \mu_n=\frac{I_x L}{e n V_x W d} \qquad (5.59) $$
