5. 정전기에너지
5.1 점전하 집단의 전기 에너지
이 장에서는 전하시스템에 저장된 정전기에너지를 구해보고자 한다.
이 정전에너지는 전하시스템이 형성되는데 투입된 총 에너지를 의미한다.
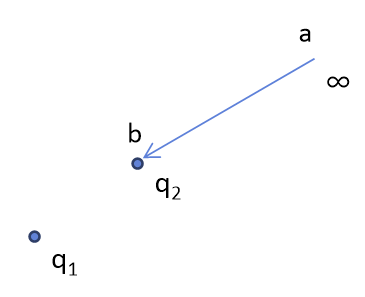
그림과 같이 물체에 힘 $\vec{F}$를 가하면서 위치 $a$에서 $b$까지 이동시켰다면,
그동안 힘 $\vec{F}$가 한 일(Work)은 다음과 같이 정의된다.
\begin{equation}
W(\mathrm{Work}) = \int_a^b \vec{F} \cdot d \vec{r}
\end{equation}
만약 이 힘이 $q_1$이 만드는 전기장에 의해 $q_2$가 받는 전기력이고,
$q_2$를 $a$에서 $b$까지 이동시키는데 드는 일은 다음과 같이 주어진다.
\begin{equation}
\begin{aligned}
W(\mathrm{Work}) & = \int_a^b \vec{F} \cdot d \vec{r} = q_2 \int_a^b \vec{E} \cdot d \vec{r} \\
& =-q_2 \int_a^b \nabla \varphi \cdot d \vec{r} = -q_2 \left(\varphi_b-\varphi_a\right)
\end{aligned}
\end{equation}
$\vec{F}$를 받아서 이동을 하게 된다면 가속을 하게 되어서 최종 위치에 왔을때는 어떤 속도를 가지게 되겠지만,
아는 바와 같이 최종 위치에서 정지해 있다.
무한대에서 정지해 있던 전하를 최종 위치까지 등속으로 이동시키면 정지된 최종 상태를 얻을수있을것인데,
이렇게 등속으로 이동시키려면 $\vec{F}$와 반대의 어떤 힘이 일을 해야하는데 이 힘이 한 일을 다음과 같이 쓸수있으며
\begin{equation}
W= q_2 \left(\varphi_b-\varphi_a\right)
\end{equation}
이 일을 정전기 에너지라고 할수있다.
만약 위치 $a$가 무한대이면
\begin{equation}
W_2 = q_2 \varphi_b = \frac{q_2 q_1}{4\pi\epsilon_0 r_{21}}
\end{equation}
$r_{21}$은 $q_2$와 $q_1$ 사이의 거리이다.
(무한대에서 가지고 온다는 것은 현재 존재하지 않는 것을 생성시킨다는 의미를 가지고 있다.)
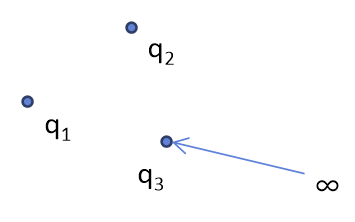
$q_1$, $q_2$, $q_3$ 이 세 전하로 이루어진 전하 시스템의 정전기 에너지를 구해보자.
이것은 $q_1$와 $q_2$가 있는 상태에서, $q_3$을 무한대에서 $\vec{r}_3$까지 가지고 오는데 투입된 에너지를 추가해서 얻는다.
이 과정에서는 $q_3$이 $q_1$과 $q_2$로 부터 전기력을 받기 때문에
이 과정에서 전기력이 한일은 다음과 같다.
$$
W_3=q_3\left(\frac{q_1}{4 \pi \epsilon_0 r_{31}}+\frac{q_2}{4 \pi \epsilon_0 r_{32}}\right)
$$
그러면 세전하 시스템이 형성되는데 투입된 총에너지(정전기에너지)는 다음과 같다.
$$
U = W_2 + W_3
$$
$N$개 전하 시스템의 정전기에너지는 다음과 같다.
$$
U=\sum_{j=1}^N W_j=\sum_{j=1}^N\left(\sum_{k=1}^{j-1} \frac{q_j q_k}{4 \pi \epsilon_0 r_{j k}}\right) .
$$
$$
U=\sum_{j=1}^N \sum_{k=1}^{j-1} W_{j k}
$$
위 식을 다음과 같이 바꾸어 쓸수도 있다.
$$
U=\frac{1}{2} \sum_{j=1}^N \sum_{k=1}^N W_{j k}, \quad\left(W_{j j}=0\right) \text {. }
$$
$$
U=\frac{1}{2} \sum_{j=1}^N \sum_{k=1}^N \frac{q_j q_k}{4 \pi \epsilon_0 r_{j k}},
$$
여기서 다음 사실을 인식한다면,
$$
\varphi_j=\sum_{k=1}^N \frac{q_k}{4 \pi \epsilon_0 r_{j k}} .
$$
정전에너지는 다음과 같이 표현될 수 있다.
\begin{equation}
U=\frac{1}{2} \sum_{j=1}^N q_j \varphi_j
\end{equation}
5.2 전하분포의 전기 에너지
이전 과정을 참고하여 부피전하밀도 $\rho$, 면전하밀도 $\sigma$로 정의되는 전하분포의 정전에너지는 다음과 같이 주어질 수 있다. $$ U=\frac{1}{2} \int_V \rho(\vec{r}) \varphi(\vec{r}) d v+\frac{1}{2} \int_S \sigma(\vec{r}) \varphi(\vec{r}) d a, $$ 전하밀도 외에 전하량 $Q_1$, $Q_2$, ... 들을 가진 도체들이 있다면, 정전에너지는 다음과 같이 주어진다. $$ U=\frac{1}{2} \int_V \rho \varphi d v+\frac{1}{2} \int_{S^{\prime}} \sigma \varphi d a+\frac{1}{2} \sum_j Q_j \varphi_j $$
5.3 전기에너지의 밀도
다음의 가우스 법칙과 가우스법칙의 미분형을 생각해보면
$$
\oint_S \vec{D} \cdot \hat{n} d a=Q
$$
$$
\vec{D} \cdot \hat{n} = \rho
$$
전하분포의 부피전전하밀도($\rho$)와 면전하밀도($\sigma$)를 각각 다음과 같이 표현할 수 있음을 알 수 있다.
$$
\rho=\nabla \cdot \vec{D}
$$
$$
\sigma=\vec{D} \cdot \hat{n}
$$
그러면 정전에너지는 다음과 같이 쓸 수 있다.
$$
U=\frac{1}{2} \int_V \varphi \nabla \cdot \vec{D} d v+\frac{1}{2} \int_S \varphi \vec{D} \cdot \hat{n} d a
$$
다음 미분 관계와 divergence 정리를 생각해본다면,
$$
\varphi \nabla \cdot \vec{D}=\nabla \cdot \varphi \vec{D}-\vec{D} \cdot \nabla \varphi .
$$
다음과 같이 적을 수 있다.
$$
U=\frac{1}{2} \int_{S+S^{\prime}} \varphi \vec{D} \cdot \hat{n}^{\prime} d a+\frac{1}{2} \int_V \vec{D} \cdot \vec{E} d v+\frac{1}{2} \int_S \varphi \vec{D} \cdot \hat{n} d a .
$$
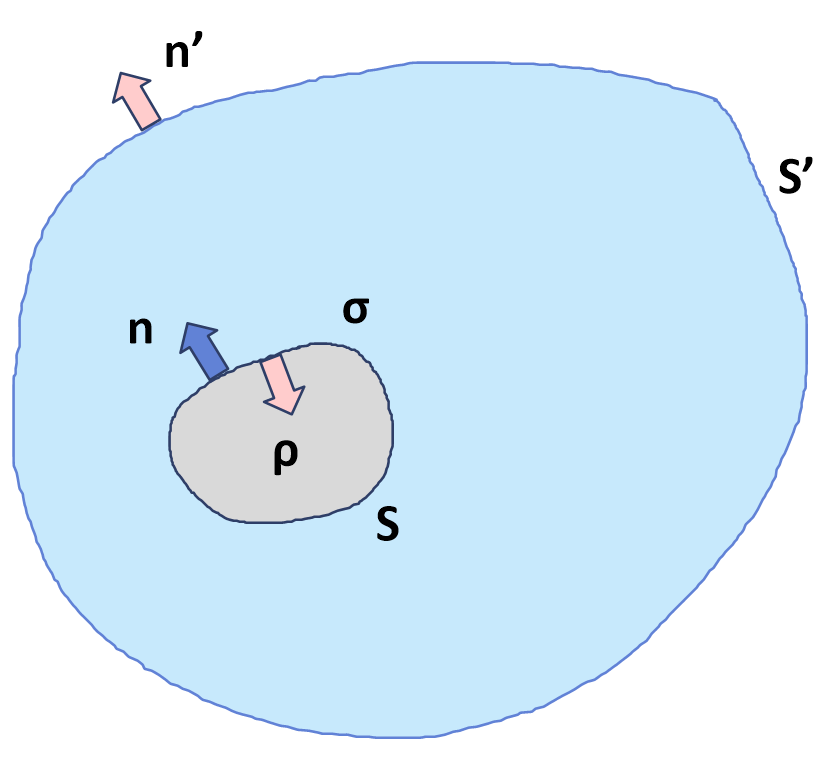
면적분은 모두 0이 되고, 부피적분만 남게 된다.
$$
U=\frac{1}{2} \int_V \vec{D} \cdot \vec{E} d v
$$
여기서 적분내의 항을 다음과 같이 에너지 밀도 $u$로 표현할 수 있다.
$$
u=\frac{1}{2} \vec{D} \cdot \vec{E}
$$
에너지 밀도는 다음과 같이 표현할수도 있다.
$$
u=\frac{1}{2} \epsilon E^2=\frac{1}{2} \frac{D^2}{\epsilon}
$$
에너지는 전기장에 저장되어 있다고 생각할 수 있다.
5.4 축전기(Capacitor)
양전하와 음전하를 저장할 수 있는 두 개의 도체 형태를 축전기라고 한다.
• 평판형 축전기
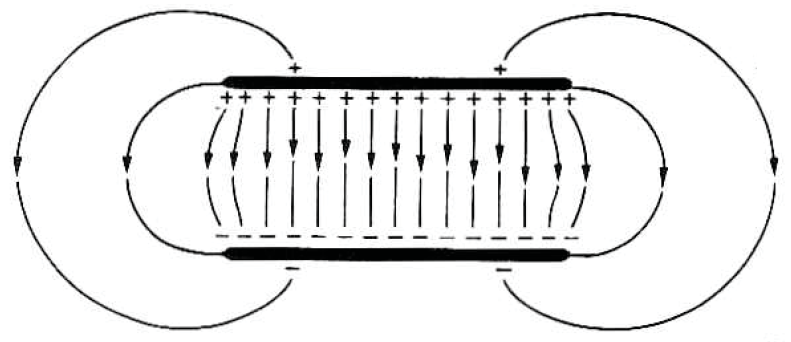
도체 판 양단에 포텐셜차이 $\Delta \varphi$를 가했을 때, 도체 판 양단에는 $+Q$와 $-Q$의 전하가 대전된다.
\begin{equation}
Q = C \Delta \varphi
\end{equation}
위와 같이 $Q$와 $\Delta \varphi$사이의 비례상수 $C$를 전기용량(capacitance)이라고 한다.
MKS 단위계에서 전기용량의 단위는 F(farad)이라고 한다. 1 F = 1 C/V.
전하계의 정전에너지인 다음 표현을 이용하면,
$$
U = \frac{1}{2} \sum_j Q_j \varphi_j
$$
축전기의 정전에너지는 다음과 같이 주어진다.
\begin{equation}
U=\frac{1}{2} Q \Delta \varphi = \frac{1}{2} C(\Delta \varphi)^2=\frac{1}{2} \frac{Q^2}{C}
\end{equation}
가우스 법칙에 의해 전기장은 다음과 같이 주어지고
$$
E=\frac{1}{\epsilon} \sigma=\frac{Q}{\epsilon A}
$$
축전기의 전기용량은 다음과 같이 평판의 면적과 거리 정보로 얻을 수 있다.
$$
C=\frac{Q}{\Delta \varphi}=\frac{\epsilon A}{d}
$$
• 구형 축전기
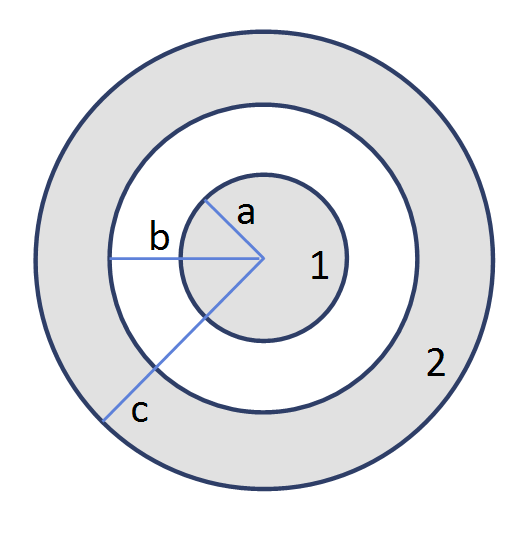
$$
\begin{aligned}
\varphi_1-\varphi_2 & =\int_1^2 \vec{E} \cdot d \vec{s}=\int_a^b E_r d r \\
& =\int_a^b \frac{Q_1 d r}{4 \pi \epsilon_0 r^2}=\frac{Q_1}{4 \pi \epsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)
\end{aligned}
$$
$$
C=\frac{Q_1}{\varphi_1-\varphi_2} = \frac{4 \pi \epsilon_0}{\left(\frac{1}{a}-\frac{1}{b}\right)}=\frac{4 \pi \epsilon_0 a b}{b-a}
$$
• 연결된 축전기
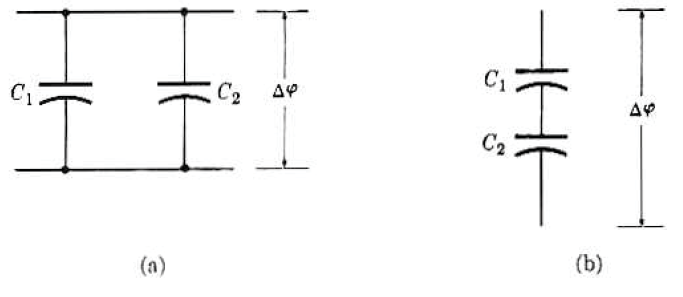
축전기가 병렬로 연결된 경우에는 동일한 포텐셜 차이 $\Delta \varphi$가 두 축전기에 걸리고,
대전되는 전하량은 $Q_1$과 $Q_2$로 다를 것이다.
$$
C=\frac{Q_{\text {total }}}{\Delta \varphi}=\frac{Q_1+Q_2}{\Delta \varphi} = C_1+C_2
$$
축전기가 직렬로 연결된 경우에는 동일한 전하량이 저장되고,
포텐셜 차이 $\Delta \varphi$는 $\Delta \varphi_1$과 $\Delta \varphi_2$로 다를 것이다.
$$
\frac{1}{C}=\frac{\Delta \varphi_1 + \Delta \varphi_2}{Q}= \frac{\Delta \varphi_1}{Q}+\frac{\Delta \varphi_2}{Q} = \frac{1}{C_1}+\frac{1}{C_2}
$$
5.5 에너지와 힘
$\vec{F}$가 물체를 거리 $d \vec{r}$ 만큼 이동시켰을때 한 일은 다음과 같다.
$$
\begin{aligned}
d W & =\vec{F} \cdot d \vec{r} \\
& =F_x d x+F_y d y+F_z d z
\end{aligned}
$$
에너지 보존 법칙에 의하면 운동에너지와 포텐셜에너지의 합은 일정하다.
즉 $K+U=\textrm{상수}$.
에너지가 보존되므로 이 전체에너지의 변화량은 0이다.
즉 $\Delta K=-\Delta U$.
일과 운동에너지와의 관계는 다음과 같으므로
$W=\Delta K$ (일한 만큼 운동에너지가 증가)
일과 포텐셜에너지와의 관계는 다음과 같이 주어진다.
$W=-\Delta U$
$$
d W=-d U
$$
$$
\begin{gathered}
-d U=F_x d x+F_y d y+F_z d z \\
F_x=-\frac{\partial U}{\partial x},
\end{gathered}
$$
결과적으로 전하들 사이의 전기력만 존재하는 전하량 $Q$가
일정하게 주어진는 상황에서는 다음과 같이 주어진다.
$$
\begin{aligned}
F_x =-\left(\frac{\partial U}{\partial x}\right)_Q
\end{aligned}
$$
만약에 축전기에 외부 건전지(battery)가 연결되어
축전기 전압이 일정하게 유지되는 경우에
전체 일의 변화에는 건전지가 한 일까지 포함된다.
\begin{equation}
d W=d W_b-d U
\end{equation}
$\varphi_j$가 일정하게 유지되는 경우 포텐셜 에너지 변화는 다음과 같고,
$$
d U=\frac{1}{2} \sum_j \varphi_j d Q_j
$$
건전지가 한 일의 변화는 다음과 같다.
$$
\begin{gathered}
d W_b=\sum_j \varphi_j d Q_j \\
d W_b=2 d U
\end{gathered}
$$
결과적으로 전기 포텐셜이 일정하게 유지되는 경우 받는 힘은 다음과 같이 주어진다.
$$
\begin{gathered}
d U=F_x d x+F_y d y+F_z d z \\
F_x=\left(\frac{\partial U}{\partial x}\right)_{\varphi}
\end{gathered}
$$
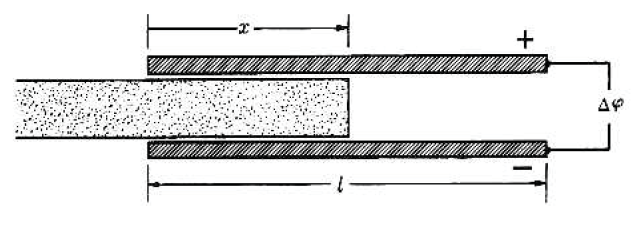
위 그림과 같이 평행판 축전기 내에 유전체가 있는 경우 정전기 에너지는 다음과 같다.
$$
U=\frac{1}{2} \int_V \epsilon E^2 d v
$$
$$
U=\frac{1}{2} \epsilon\left(\frac{\Delta \varphi}{d}\right)^2 d w x+\frac{1}{2} \epsilon_0\left(\frac{\Delta \varphi}{d}\right)^2 d w(l-x)
$$
건전지가 연결된 경우 유전체가 받는 힘은 다음과 같다.
$$
F_x=\frac{1}{2}\left(\epsilon-\epsilon_0\right) w \frac{(\Delta \varphi)^2}{d}=\frac{1}{2}(K-1) \epsilon_0 E^2 A
$$