6. 반도체 내에서의 비평형 과잉운반자
4장까지는 열평형 상태에 있는 반도체를 기술하였다.
반도체 소자에 전류가 흐르는 것은 반도체가 비평형상태에 있다는 것을 의미한다.
그래서 5장에서 다루어진 전류의 기술 방식도 엄밀하게는 비평형 상태로 기술해야 하지만,
평형상태를 과도하게 벗어나지 않았다는 가정하에 기술되었다.
이 장에서는 비평형상태를 이해하는 첫번째 단계로 외부 여기(exitation)에 의한
과잉 전자와 과잉 홀의 거동에 대해서 기술한다.
6.1 운반자 생성 및 재결합(CARRIER GENERATION AND RECOMBINATION)
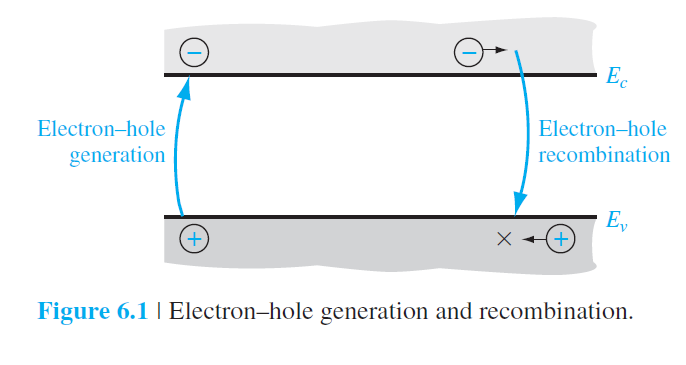
운반자의 생성은 valence 밴드의 전자가 외부 여기를 통해 conduction 밴드로 상승 이동을 함으로써 conduction 밴드의 운반자(전자) 농도와 valence 밴드의 운반자(홀) 농도가 증가되는 되는 과정이고, 운반자의 재결합은 conduction 밴드에 있던 전자가 valence 밴드로 하락 이동을 함으로써 conduction 밴드의 운반자(전자) 농도와 valence 밴드의 운반자(홀) 농도가 감소되는 과정이다.
6.1.1 평형 상태의 반도체
어떤 특정온도에서 valence 밴드의 전자가 conduction 밴드로의 상승 이동은 지속적으로 발생하고 있고,
이와동시에 conduction 밴드의 전자가 valence 밴드로의 하락 또한 지속적으로 발생한다.
conduction 밴드의 전자가 valence 밴드로 하락하는 것을 실공간에서는 관측한다면 결정내에 이동하던 전자가 전자가 비어있는 자리(홀)를 차지하는 것으로 기술할 수 있다.
아때 가지고 있던 운동에너지는 격자로 이동된다.
이러한 생성과 재결합이 균형을 이루게 되면 열평형상태가 된다.
열평형상태에서 운반자로서의 전자와 홀의 생성율 각각 $G_{n 0}$과 $G_{p 0}$로 표현한다면 다음의 관계가 성립할 것이다.
$$ G_{n 0}=G_{p 0} $$
열평형상태에서 운반자로서의 전자와 홀의 재결합율을 각각 $R_{n 0}$과 $R_{p 0}$로 표현한다면 다음의 관계가 성립할 것이다.
$$ R_{n 0}=R_{p 0} $$
열평형상태가 되기 위해서는 운반자가 생성된 만큼 감소해야하는 것이므로 결과적으로 다음이 성립한다.
$$ G_{n 0}=G_{p 0}=R_{n 0}=R_{p 0} $$
생성율과 재결합율의 단위는 cm$^{-3}$/s 으로 주어진다.
6.1.2 과잉운반자의 생성 및 재결합
고에너지 광자의 주입이나 일시적인 온도 상승에 의해서
평형상태를 벗어나는 과잉전자(excess electron)와 과잉 홀(excess hole)이 쌍으로 발생할 수 있다.
과잉전자와 과잉 홀의 생성율을 각각 $g_n'$과 $g_p'$로 표기하면 다음과 같이 기술될 수 있다.
$$ g_n'=g_p' \qquad (6.4)$$
과잉전자의 농도와 과잉 홀의 농도를 각각 $\delta n$과 $\delta p$로 표기하면,
conduction 밴드의 전자의 농도 $n$과 valence 밴드의 홀의 농도 $p$는 다음과 같이 기술될 수 있다.
\begin{aligned}
&n=n_0+\delta n \qquad (6.5a)\\
&p=p_0+\delta p \qquad (6.5b)
\end{aligned}
여기서 $n_0$와 $p_0$ 각각 평형상태에서의 전자와 홀의 농도이다.
위 식은 비평형상태에서는 $np \neq n_0 p_0 = n_i^2$임을 알수있다.
그림 6.2는 과잉전자와 과잉홀의 생성과정과 그로 인한 운반자 농도를 나타내고 있다.
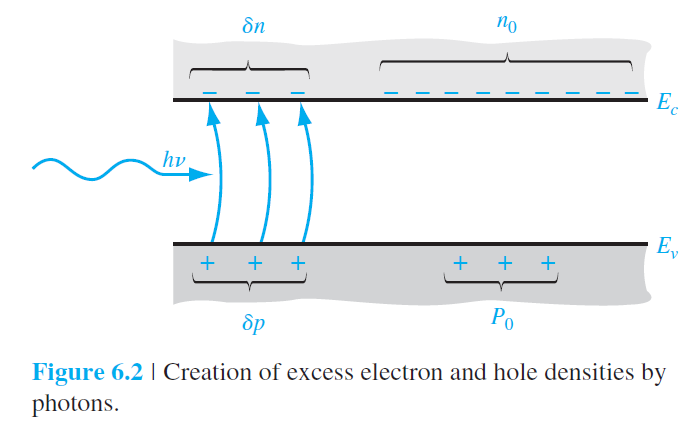
그림 6.3은 과잉전자와 과잉홀의 소멸과정과 그로 인한 운반자 농도를 나타내고 있다.
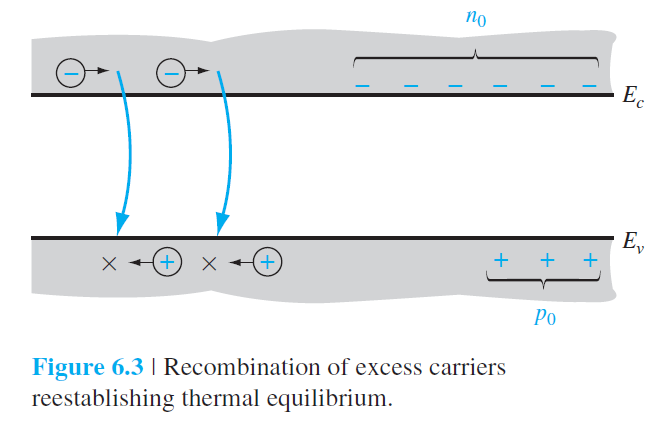
과잉 운반자의 재결합율은 다음과 같이 기술될 수 있다.
$$ R_n' = R_p' \qquad (6.6)$$
밴드와 밴드간의 직접 재결합을 고려하면,
재결합은 자발적으로 일어난다.
그래서 전자와 홀의 재결합율은 시간에 관계없이 일정하다.
이 장에서는 비슷비슷한 기호들이 많이 등장하는데, 표 6.1에서 정리되어 있다.
| $n_0, p_0$ | 열평형 전자의 농도와 홀의 농도(대개 시간과 위치에 대해 일정한 값을 가짐) |
| $n, p$ | 총 전자 농도와 홀의 농도(시간과 위치의 함수) |
| $\delta n=n-n_0$ $\delta p=p-p_0$ |
과잉 전자의 농도와 과잉 홀의 농도(시간과 위치의 함수) |
| $g_n', g_p'$ | 과잉전자와 과잉홀의 생성율 |
| $R_n', R_p'$ | 과잉전자와 과잉홀의 재결합율 |
| $\tau_{n 0}, \tau_{p 0}$ | 과잉 소수 운반자의 수명 |
전자농도의 순 변화율은 다음과 같이 기술될 수 있다.
$$ \frac{d n(t)}{d t}=\alpha_r\left[n_i^2-n(t) p(t)\right] \qquad (6.7)$$
여기서 $n(t)$과 $p(t)$는 다음과 같이 주어진다.
$$
\begin{aligned}
& n(t)=n_0+\delta n(t) \qquad (6.8a) \\
& p(t)=p_0+\delta p(t) \qquad (6.8b)
\end{aligned}
$$
(6.7)식 우변의 첫째항 $\alpha_r n_i^2$은 생성율을 둘째항은 재결합율을 나타낸다.
재결합율이 그렇게 가정되는 이유는 재결합율은 전자와 홀의 농도에 비례해야 하기 때문이다.
(6.7)식은 평형상태가 되면 전자농도의 순 변화율은 0이 되도록 설정되어 있다.
(6.8)식을 (6.7)식에 대입하면 다음이 얻어진다.
$$
\begin{aligned}
\frac{d(\delta n(t))}{d t} & =\alpha_r\left[n_i^2-\left(n_0+\delta n(t)\right)\left(p_0+\delta p(t)\right)\right] \\
& =-\alpha_r \delta n(t)\left[\left(n_0+p_0\right)+\delta n(t)\right] \qquad (6.9)
\end{aligned}
$$
고-수준 주입은 $\delta n \gg n_0$을 의미하고,
저-수준 주입은 $\delta n \ll n_0$을 의미한다.
(6.9)식은 저-수준 주입에서 쉽게 풀리므로, 저-수준 주입인 경우를 논의해 본다.
P형 반도체($p_0\gg n_0$)에서 저-수준 주입($\delta n(t) \ll p_0$)이면 (6.9)식은 다음과 같이 된다.
$$
\frac{d(\delta n(t))}{d t}=-\alpha_r p_0 \delta n(t) \qquad (6.10)
$$
이 식의 해는 다음과 같이 시간에 따라 지수함수적으로 감소하는 형태로 나타난다.
$$ \delta n(t)=\delta n(0) e^{-\alpha_r p_0 t}=\delta n(0) e^{-t / \tau_{n 0}} \qquad (6.11)$$
$\tau_{n 0}=(\alpha_r p_0)^{-1}$는 과잉 소수 운반자 수명(excess minority carrier lifetime)이라고 하며, 저-수준 주입일때 일정하다.
(6.10)식으로부터 과잉 소수 운반자 전자의 재결합율은 다음과 같이 주어진다.
$$ R_n'=\frac{-d(\delta n(t))}{d t}=+\alpha_r p_0 \delta n(t)=\frac{\delta n(t)}{\tau_{n 0}} $$
(6.6)식에 의하여 과잉 다수 운반자 홀의 재결합율은 다음과 같이 주어진다.
$$ R_n'=R_p'=\frac{\delta n(t)}{\tau_{n 0}} $$
N형 반도체($n_0\gg p_0$)에서 저-수준 주입($\delta p(t) \ll n_0$)이면, 재 결합율은 다음과 같이 주어진다.
$$ R_n'=R_p'=\frac{\delta n(t)}{\tau_{p 0}} $$
6.2 과잉운반자의 특성들
6.2.1 연속방정식
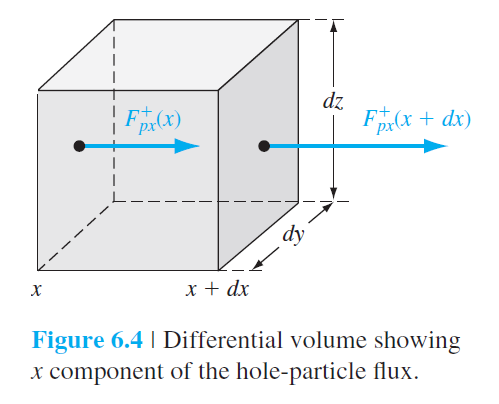
$$F_{p x}^{+}(x+d x)=F_{p x}^{+}(x)+\frac{\partial F_{p x}^{+}}{\partial x} \cdot d x$$
$$
\begin{aligned}
& \frac{\partial p}{\partial t} d x d y d z =\left[F_{p x}^{+}(x)-F_{p x}^{+}(x+d x)\right] d y d z \\
& =-\frac{\partial F_{p x}^{+}}{\partial x} d x d y d z \qquad (6.16)\\
& \frac{\partial p}{\partial t} d x d y d z \\
& =-\frac{\partial F_p^{+}}{\partial x} d x d y d z+g_p d x d y d z-\frac{p}{\tau_{p t}} d x d y d z \qquad (6.17)
\end{aligned}
$$
$$
\frac{\partial p}{\partial t}=-\frac{\partial F_p^{+}}{\partial x}+g_p-\frac{p}{\tau_{p t}}
$$
$$
\frac{\partial n}{\partial t}=-\frac{\partial F_n^{-}}{\partial x}+g_n-\frac{n}{\tau_{n t}}
$$

6.2.2 시간의존 확산 방정식
$$ \begin{aligned} & J_p=e \mu_p p \mathrm{E}-e D_p \frac{\partial p}{\partial x} \\ & J_n=e \mu_n n \mathrm{E}+e D_n \frac{\partial n}{\partial x} \end{aligned} $$ $$ \begin{gathered} \frac{J_p}{(+e)}=F_p^{+}=\mu_p p \mathrm{E}-D_p \frac{\partial p}{\partial x} \\ \frac{J_n}{(-e)}=F_n^{-}=-\mu_n n \mathrm{E}-D_n \frac{\partial n}{\partial x} \end{gathered} $$ $$ \begin{aligned} & \frac{\partial p}{\partial t}=-\mu_p \frac{\partial(p \mathrm{E})}{\partial x}+D_p \frac{\partial^2 p}{\partial x^2}+g_p-\frac{p}{\tau_{p t}} \\ & \frac{\partial n}{\partial t}=+\mu_n \frac{\partial(n \mathrm{E})}{\partial x}+D_n \frac{\partial^2 n}{\partial x^2}+g_n-\frac{n}{\tau_{n t}} \end{aligned} $$ $$ \frac{\partial(p \mathrm{E})}{\partial x}=\mathrm{E} \frac{\partial p}{\partial x}+p \frac{\partial \mathrm{E}}{\partial x} $$ $$ \begin{aligned} & D_p \frac{\partial^2 p}{\partial x^2}-\mu_p\left(\mathrm{E} \frac{\partial p}{\partial x}+p \frac{\partial \mathrm{E}}{\partial x}\right)+g_p-\frac{p}{\tau_{p t}}=\frac{\partial p}{\partial t} \\ & D_n \frac{\partial^2 n}{\partial x^2}+\mu_n\left(\mathrm{E} \frac{\partial n}{\partial x}+n \frac{\partial \mathrm{E}}{\partial x}\right)+g_n-\frac{n}{\tau_{n t}}=\frac{\partial n}{\partial t} \end{aligned} $$ $$ \begin{aligned} & D_p \frac{\partial^2(\delta p)}{\partial x^2}-\mu_p\left(\mathrm{E} \frac{\partial(\delta p)}{\partial x}+p \frac{\partial \mathrm{E}}{\partial x}\right)+g_p-\frac{p}{\tau_{p t}} =\frac{\partial(\delta p)}{\partial t} \qquad (6.29)\\ & D_n \frac{\partial^2(\delta n)}{\partial x^2}+\mu_n\left(\mathrm{E} \frac{\partial(\delta n)}{\partial x}+n \frac{\partial \mathrm{E}}{\partial x}\right)+g_n-\frac{n}{\tau_{n t}} =\frac{\partial(\delta n)}{\partial t} \qquad (6.30) \end{aligned} $$
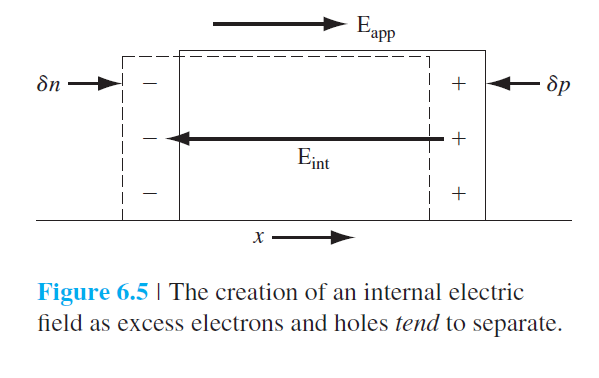
6.3 Ambipolar 수송
6.3.1 Ambipolar 수송방정식의 유도
$$
\mathrm{E}=\mathrm{E}_{\text {app }}+\mathrm{E}_{\mathrm{int}}
$$
$$
\nabla \cdot \mathrm{E}_{\mathrm{int}}=\frac{e(\delta p-\delta n)}{\epsilon_s}=\frac{\partial \mathrm{E}_{\mathrm{int}}}{\partial x}
$$
$$
\left|\mathrm{E}_{\text {int }}\right| \ll\left|\mathrm{E}_{\text {app }}\right|
$$
$$
g_n=g_p \equiv g
$$
$$
R_n=\frac{n}{\tau_{n t}}=R_p=\frac{p}{\tau_{p t}} \equiv R
$$
$$
\begin{aligned}
& D_p \frac{\partial^2(\delta n)}{\partial x^2}-\mu_p\left(\mathrm{E} \frac{\partial(\delta n)}{\partial x}+p \frac{\partial \mathrm{E}}{\partial x}\right)+g-R=\frac{\partial(\delta n)}{\partial t} \\
& D_n \frac{\partial^2(\delta n)}{\partial x^2}+\mu_n\left(\mathrm{E} \frac{\partial(\delta n)}{\partial x}+n \frac{\partial \mathrm{E}}{\partial x}\right)+g-R=\frac{\partial(\delta n)}{\partial t}
\end{aligned}
$$
$$
\begin{gathered}
\left(\mu_n n D_p+\mu_p p D_n\right) \frac{\partial^2(\delta n)}{\partial x^2}+\left(\mu_n \mu_p\right)(p-n) \mathrm{E} \frac{\partial(\delta n)}{\partial x} \\
+\left(\mu_n n+\mu_p p\right)(g-R)=\left(\mu_n n+\mu_p p\right) \frac{\partial(\delta n)}{\partial t}
\end{gathered}
$$
$$
D' \frac{\partial^2(\delta n)}{\partial x^2}+\mu' \mathrm{E} \frac{\partial(\delta n)}{\partial x}+g-R=\frac{\partial(\delta n)}{\partial t} \qquad (6.39)
$$
위 식을 ambipolar 수송방정식이라고 한다.
$$
D'=\frac{\mu_n n D_p+\mu_p p D_n}{\mu_n n+\mu_p p}
$$
$$ \mu'=\frac{\mu_n \mu_p(p-n)}{\mu_n n+\mu_p p} \qquad (6.41) $$
(6.41)식을 ambipolar 이동도라고 한다.
$$ \frac{\mu_n}{D_n}=\frac{\mu_p}{D_p}=\frac{e}{k T} $$
$$ D'=\frac{D_n D_p(n+p)}{D_n n+D_p p} \qquad (6.43)$$
(6.43)식을 ambipolar 확산계수라고 한다.
6.3.2 외인성 도핑 반도체에서 과잉 운반자 거동(저-수준 주입인 경우)
(6.3.1)절은 진성 반도체에서의 과잉 운반자를 다루었다.
이번 절에는 외인성 반도체에서의 과잉 운반자 거동을 다룬다.
(6.43)식은 다음과 같이 쓸수있다.
$$ D'=\frac{D_n D_p\left[\left(n_0+\delta n\right)+\left(p_0+\delta n\right)\right]}{D_n\left(n_0+\delta n\right)+D_p\left(p_0+\delta n\right)} \qquad (6.44) $$
P형 반도체라면 $p_0\gg n_0$을 가정할 수 있다.
저-수준 주입이라면 $p_0\gg \delta n$을 가정할 수 있다.
이 가정들을 적용하면 (6.44)은 다음과 같이 된다.
$$ D'=D_n \qquad (6.45) $$
동일한 가정하에 (6.41)식은 다음과 같이 된다.
$$ \mu'=\mu_n \qquad (6.46) $$
저-수준 주입의 N형 반도체라면 다음이 성립한다.
$$ D'=D_p \qquad (6.47) $$
$$ \mu'=-\mu_p \qquad (6.48) $$
결과적으로 저-수준 주입 반도체에서의 ambipolar 이동도 및 확산계수는 소수 운반자 값들로 정해진다는 사실에 유의하자.
$$
g-R=g_n-R_n=\left(G_{n 0}+g_n'\right)-\left(R_{n 0}+R_n'\right)
$$
$$
G_{n 0}=R_{n 0}
$$
$$
g-R=g_n'-R_n'=g_n'-\frac{\delta n}{\tau_n}
$$
$$
g-R=g_p-R_p=\left(G_{p 0}+g_p'\right)-\left(R_{p 0}+R_p'\right)
$$
$$
G_{p 0}=R_{p 0}
$$
$$ g-R = g_p'-R_p' = g_p'-\frac{\delta p}{\tau_p} $$
저-주입 P형 반도체에서 ambipolar 수송 방정식은 다음과 같다.
$$ D_n \frac{\partial^2(\delta n)}{\partial x^2}+\mu_n \mathrm{E} \frac{\partial(\delta n)}{\partial x}+g'-\frac{\delta n}{\tau_{n 0}}
=\frac{\partial(\delta n)}{\partial t} \qquad (6.55) $$
저-주입 N형 반도체에서 ambipolar 수송 방정식은 다음과 같다.
$$ D_p \frac{\partial^2(\delta p)}{\partial x^2}-\mu_p \mathrm{E} \frac{\partial(\delta p)}{\partial x}+g'-\frac{\delta p}{\tau_{p 0}}
=\frac{\partial(\delta p)}{\partial t} \qquad (6.56) $$
6.3.3 Ambipolar 수송방정식의 적용


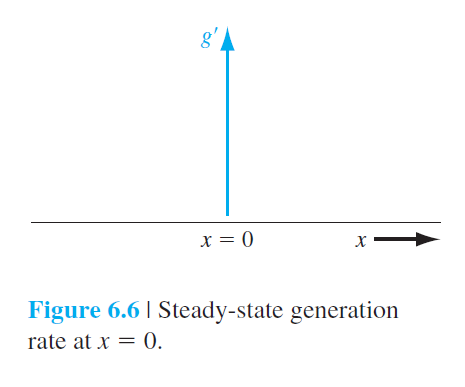

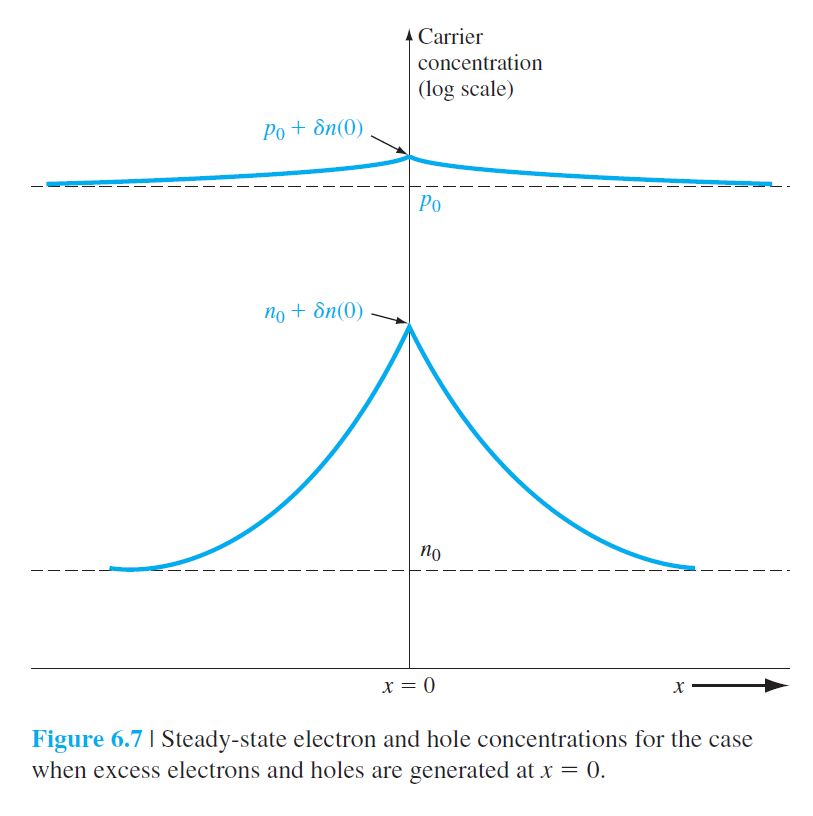

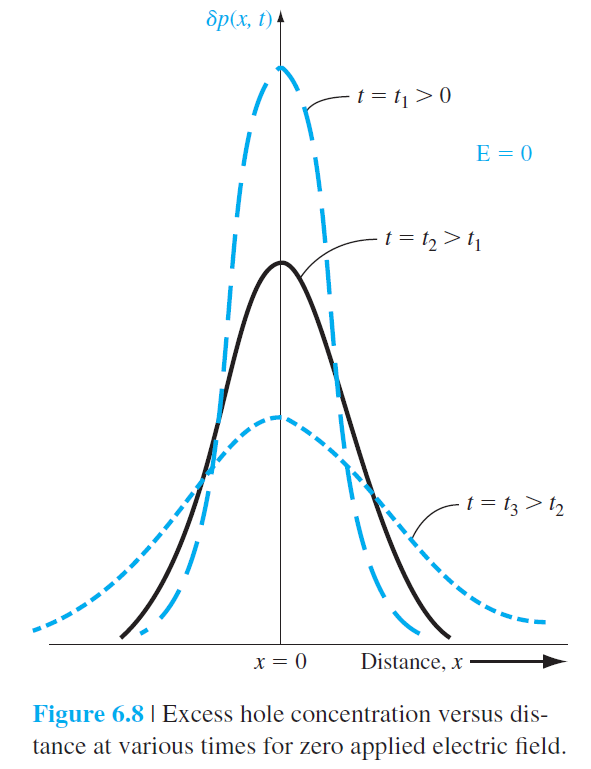
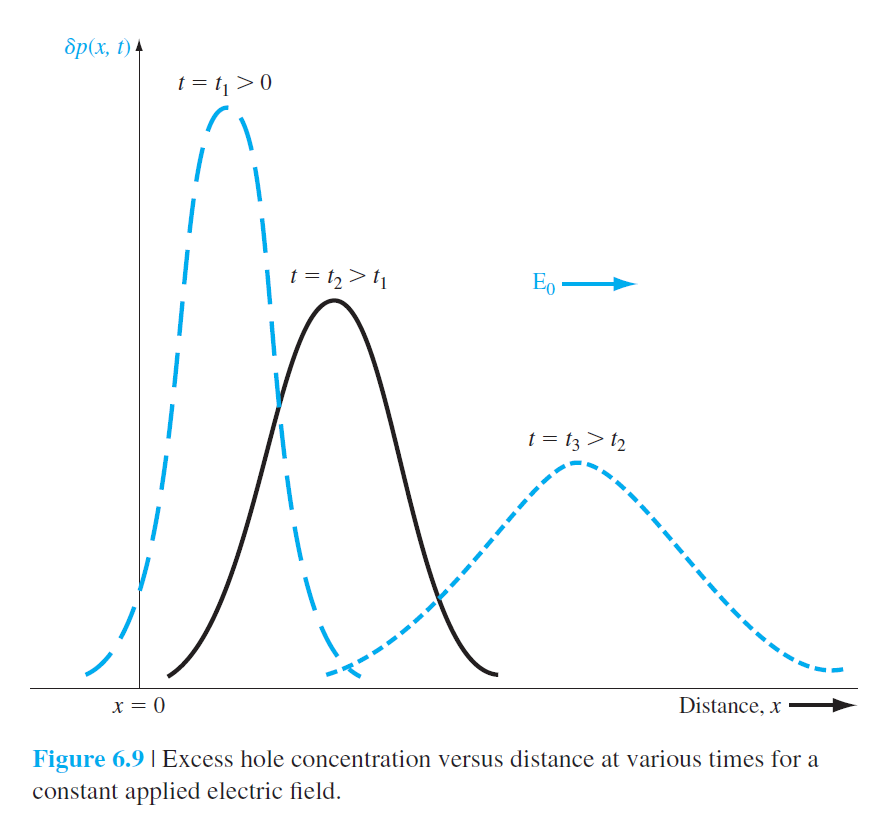
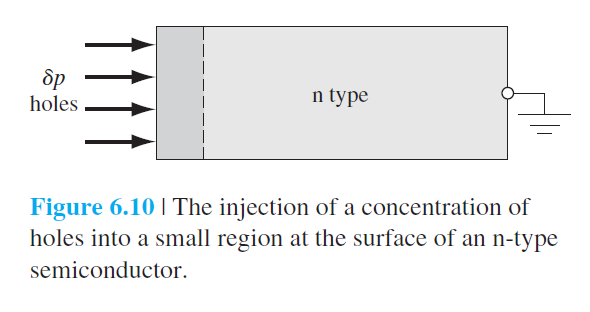
6.3.4 유전 이완시간상수(Dielectric Relaxation Time Constant)
$$
\nabla \cdot \mathrm{E}=\frac{\rho}{\epsilon}
$$
$$
J=\sigma \mathrm{E}
$$
$$
\nabla \cdot J=-\frac{\partial \rho}{\partial t}
$$
$$
\nabla \cdot J=\sigma \nabla \cdot E=\frac{\sigma \rho}{\epsilon}
$$
$$
\frac{\sigma \rho}{\epsilon}=-\frac{\partial \rho}{\partial t}=-\frac{d \rho}{d t}
$$
$$
\frac{d \rho}{d t}+\left(\frac{\sigma}{\epsilon}\right) \rho=0
$$
$$
\rho(t)=\rho(0) e^{-\left(t / \tau_d\right)}
$$
$$
\tau_d=\frac{\epsilon}{\sigma}
$$

6.3.5 Haynes–Shockley 실험
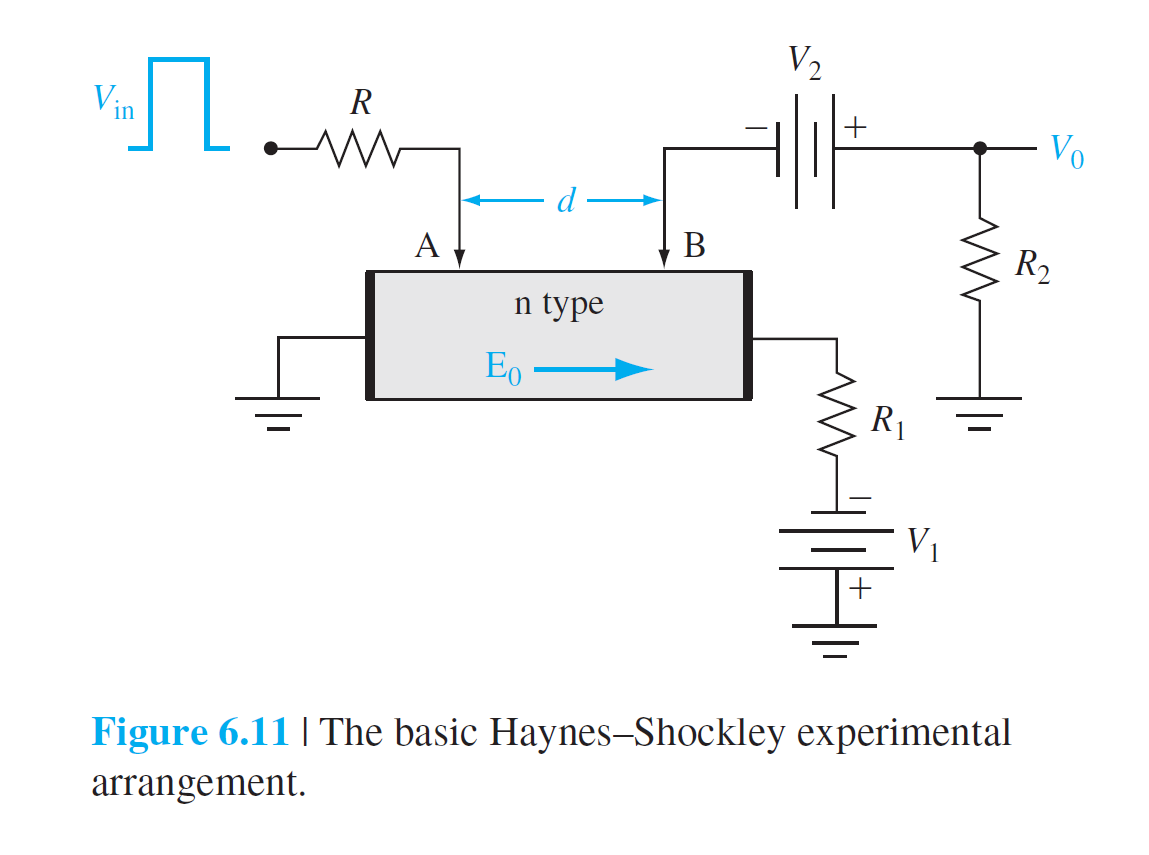
6.4 Quasi-Fermi 에너지 준위
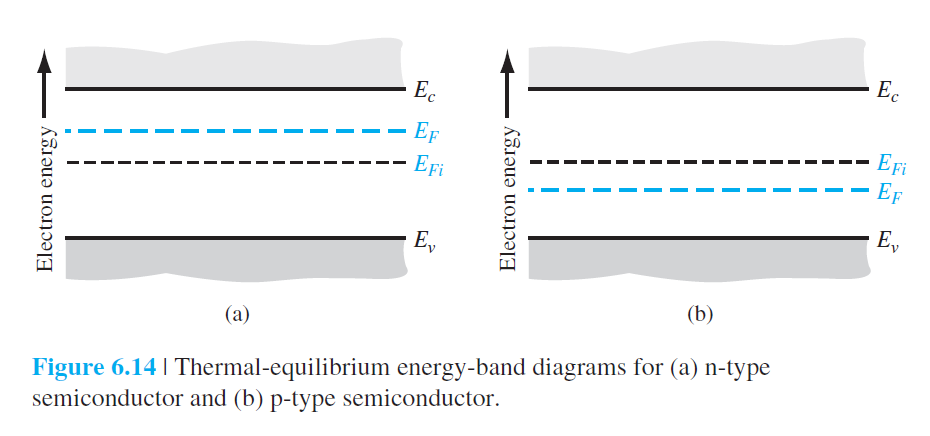
열평형상태일때 전자와 홀의 농도는 Fermi 준위와 깊은 관련이 있으며 다음과 같이 주어지는 것을 우리는 이미 배웠다.
$$
\begin{aligned}
& n_0=n_i \exp \left(\frac{E_F-E_{F i}}{k T}\right) \qquad (6.84a)\\
& p_0=n_i \exp \left(\frac{E_{F i}-E_F}{k T}\right) \qquad (6.84b)
\end{aligned}
$$
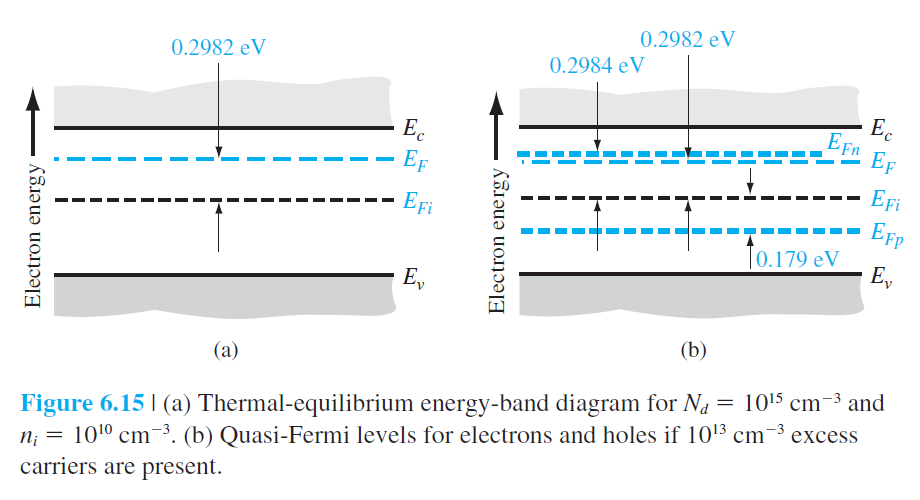
그림 6.14는 N형 반도체와 P형 반도체에서 Fermi 준위를 기술하고 있다.
과잉운반자가 존재하는 상황에서는 열평형상태가 아니기 때문에 Fermi 준위가 정의되지 않는다.
그러나 이러한 비평형상태에서도 어쨌든 전체농도(평형농도 + 과잉농도)는 정의되므로
Fermi 준위에 대응되는 quasi-Fermi 준위를 정의할 수 있다.
전자와 홀의 전체 농도에 대한 표시를 (6.84)식 형식으로 쓰면 다음과 같이 기술될 수 있다.
$$
\begin{aligned}
& n_0+\delta n=n_i \exp \left(\frac{E_{F n}-E_{F i}}{k T}\right) \qquad (6.85a) \\
& p_0+\delta p=n_i \exp \left(\frac{E_{F i}-E_{F p}}{k T}\right) \qquad (6.85b)
\end{aligned}
$$
여기서 $E_{F n}$와 $E_{F p}$는 각각 전자와 홀의 quasi-Fermi 준위들이다.

6.5 과잉 운반자의 수명
6.5.1 재결합에 대한 Shockley–Read–Hall 이론
• trap
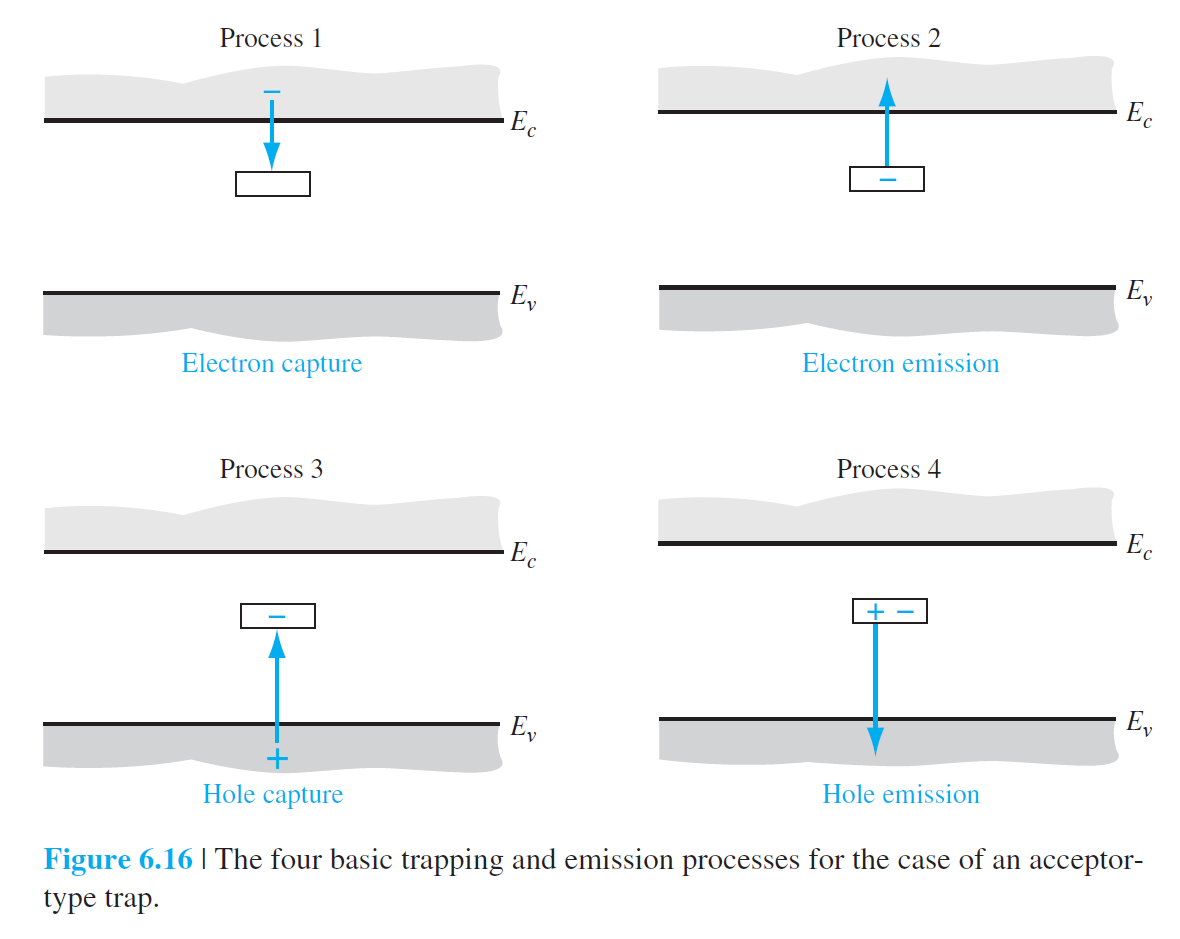
donor나 acceptor와는 달리 trap은 전자와 홀 둘다 포획하거나 방출할 수 있다.
전자가 trap에너지 준위(E_t)에 존재할 확율은 다음과 같이 주어진다.
$$ f_F\left(E_t\right)=\frac{1}{1+\exp \left(\frac{E_t-E_F}{k T}\right)} \qquad (6.87) $$
• 과정1
conduction 밴드에 있던 전자가 trap에 포획되는 비율은 다음과 같이 주어진다.
$$ R_{c n}=C_n N_t\left[1-f_F\left(E_t\right)\right] n \qquad (6.86)$$
$C_n$ : 전자 포획 단면적 비례 상수
$N_t$ : trap 원자의 농도
$n$ : conduction 밴드의 전자 농도
• 과정2
trap에 있던 전자가 conduction 밴드로 방출되는 비율은 다음과 같이 주어진다.
$$ R_{e n}=E_n N_t f_F\left(E_t\right) $$
$E_n$ : 전자 포획 단면적 비례 상수
$N_t$ : trap 원자의 농도
• 열평형상태
열평형상태에서는 포획율과 방출율이 같아야 하기 때문에 다음이 성립한다.
$$ R_{e n}=R_{c n} \qquad (6.89) $$
이 식은 다음과 같이 쓸 수 있다.
$$ E_n N_t f_{F 0}\left(E_t\right)=C_n N_t\left[1-f_{F 0}\left(E_t\right)\right] n_0 \qquad (6.90)$$
여기서 $n$는 열평형 값인 $n_0$로 대체 되었다.
$f_{F 0}$을 Boltzmann 근사로 대체하면 다음 식이 얻어진다.
$$ E_n=n' C_n \qquad (6.91) $$
여기서 $n'$은 다음과 같이 주어진다.
$$ n'=N_c \exp \left[\frac{-\left(E_c-E_t\right)}{k T}\right] \qquad (6.92) $$
conduction 밴드에 있던 전자가 trap에 포획되는 순비율은 다음과 같이 주어진다.
$$ R_n = R_{c n}-R_{e n} $$
$$ R_n=\left[C_n N_t\left(1-f_F\left(E_t\right)\right) n\right]-\left[E_n N_t f_F\left(E_t\right)\right] $$
(6.91)식을 이용하면 다음이 얻어진다.
$$ R_n=C_n N_t\left[n\left(1-f_F\left(E_t\right)\right)-n' f_F\left(E_t\right)\right] \qquad (6.95)$$
• 과정 3과 4
$$ R_p=C_p N_t\left[p f_F\left(E_t\right)-p'\left(1-f_F\left(E_t\right)\right)\right] \qquad (6.96)$$
$$ p'=N_v \exp \left[\frac{-\left(E_t-E_v\right)}{k T}\right] $$
• 종합
trap 농도가 과도하지 않다면, 과잉전자와 과잉 홀의 농도가 같고, 전자와 홀의 재결합율은 같다.
(6.95)식과 (6.96)을 연립하면 다음 식을 얻는다.
$$ f_F\left(E_t\right)=\frac{C_n n+C_p p'}{C_n\left(n+n'\right)+C_p\left(p+p'\right)} \qquad (6.98) $$
$n'p' = n_i^2$임을 생각하면, 다음이 얻어진다.
$$ R_n=R_p=\frac{C_n C_p N_t\left(n p-n_i^2\right)}{C_n\left(n+n'\right)+C_p\left(p+p'\right)} \equiv R \qquad (6.99) $$
열평형상태에서는 $np = n_i^2$ 이므로 $R_n=R_p=0$임을 확인할 수 있다.
(6.99)식은 재결합율이므로 다음과 같이 쓸수있다.
$$ R=\frac{\delta n}{\tau} \qquad (6.100) $$
여기서 $\delta n$는 과일 운반자의 농도 $\tau$는 과잉운반자의 수명이다.
6.5.2 외인성 도핑 반도체인 경우(저-수준 주입인 경우)
저주입 $N$형 반도체
$$
n_0 \gg p_0, \quad n_0 \gg \delta p, \quad n_0 \gg n', \quad n_0 \gg p'
$$
$$
R=C_p N_t \delta p
$$
$$
R=\frac{\delta n}{\tau}=C_p N_t \delta p \equiv \frac{\delta p}{\tau_{p 0}} \\
$$
$$
\tau_{p 0}=\frac{1}{C_p N_t}
$$
저주입 $P$형 반도체
$$
p_0 \gg n_0, \quad p_0 \gg \delta n, \quad p_0 \gg n', \quad p_0 \gg p'
$$
\begin{equation}
\tau_{n 0}=\frac{1}{C_n N_t}
\end{equation}

6.6 표면 효과
6.6.1 표면 상태들
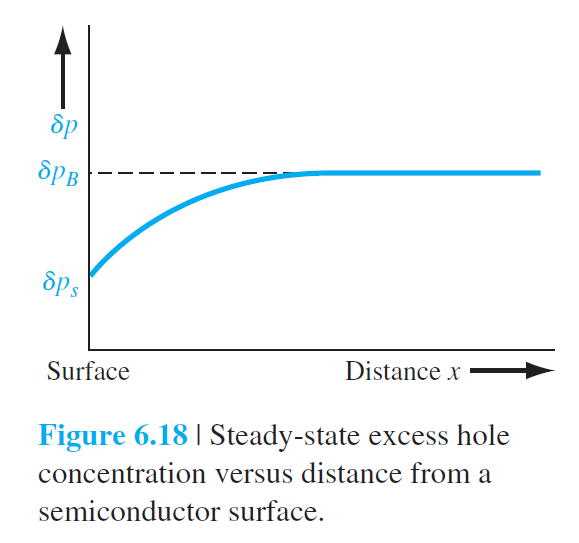
$N$형 반도체의 bulk에서 과잉 운반자 재결합율
$$ R=\frac{\delta p}{\tau_{p 0}} \equiv \frac{\delta p_B}{\tau_{p 0}} \qquad (6.106)$$
$N$형 반도체의 표면에서 과잉 운반자 재결합율
$$ R_s=\frac{\delta p_s}{\tau_{p 0 s}} \qquad (6.107)$$

6.6.2 표면 재결합 속도
\begin{equation}
-\left.D_p\left[\hat{n} \cdot \frac{d(\delta p)}{d x}\right]\right|_{\text {surf }}=\left.s \delta p\right|_{\text {surf }}
\end{equation}
$$
\left.D_p \frac{d(\delta p)}{d x}\right|_{\text {surf }}=\left.s \delta p\right|_{\text {surf }}
$$
$$
\begin{gathered}
\delta p_{\text {surf }}=\delta p(0)=g' \tau_{p 0}+B \\
\left.\frac{d(\delta p)}{d x}\right|_{\text {surf }}=\left.\frac{d(\delta p)}{d x}\right|_{x=0}=-\frac{B}{L_p}
\end{gathered}
$$
$$
B=\frac{-s g' \tau_{p 0}}{\left(D_p / L_p\right)+s}
$$
$$
\delta p(x)=g' \tau_{p 0}\left(1-\frac{s L_p e^{-x / L_p}}{D_p+s L_p}\right)
$$
