6. 전류

6.1 전하의 흐름

6.2.1 전류의 정의

물질을 이루는 원자는 양성자와 중성자로 이루어진 핵과 거기에 속박되어 그 주위를 돌고 있는 전자들로 이루어져 있다. 도체의 경우에는 그 전자들 중에서 최외각의 전자들이 속박에서 벗어나서 자유롭게 움직일 수 있는 경우가 많다. 이 전자들이 도체에서 전류의 원인이 된다.





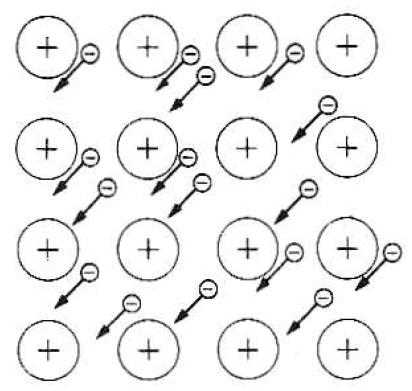
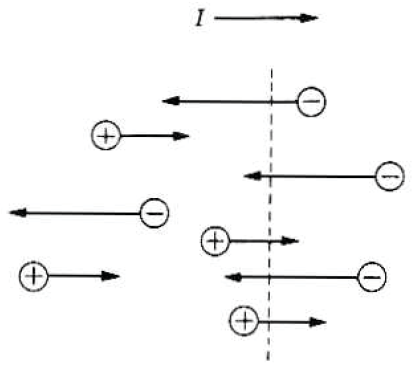
역사적으로 전자가 전류의 원인이라고 밝혀지기전에 관례적으로 양전하의 흐름을 전류라고 정의가 되었다. 그러나 실제적으로 움직이는 것은 음의 전하를 가진 전자이기 때문에, 전류의 방향은 전자의 운동방향의 반대방향으로 정의될 수 있다.
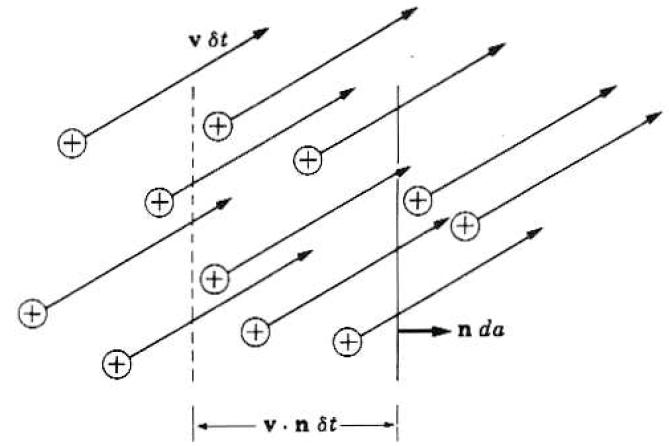
전류의 관례적 정의는 다음과 같다. 동영상에서 보는 것 처럼, 전하들이 시간 $t$동안 어떤 단면적이 $A$인 면 $S$을 통과할 때, 평균 전류는 다음과 같이 개념적으로 쓸 수 있다. $$I_{\mathrm{평균}}=\frac{ \mathrm{ 시간 t동안 면 A를 통과한 전하량} }{t}$$ 전류의 단위는 ampere라고 하며, 다음과 같은 차원을 가진다. \begin{equation} 1 \text { ampere }=1 \frac{\text { coulomb }}{\text { second }} \end{equation} 실제적으로는 매순간 혹은 면적 $A$에 모든 지점에서 전하의 흐름이 다를 수 있으므로, 좀더 정량적으로 전류를 다음과 같이 정의한다. 면적 $A$중의 극히 일부 면적인 $da$를 시간 $\delta t$ 동안 통과한 전하량을 $\delta Q$ 이라고 하자. $da$를 통과한 전류 $dI$는 다음과 같다. $$dI=\frac{\delta Q}{\delta t}$$ 만약 단위 부피당 전하의 갯수 $N$과 전하 하나당 전하량 $q$가 알려져 있다면, $\delta Q$는 다음과 같이 쓸 수 있다. $$\delta Q = q N (\vec{v} \cdot \hat{n} \delta t da) $$ 여기서 $\hat{n}$는 ㅁㄴ에 수직인 단위 벡터, $\vec{v}$는 전하들의 이동 속도이고, $\vec{v} \cdot \hat{n} \delta t d a$는 시간 $\delta t$동안 면 $da$을 통과한 전하영역의 부피이다. 그러면 $dI$는 다음과 같다. \begin{equation} \begin{aligned} d I & =\frac{\delta Q}{\delta t}=\frac{q N \vec{v} \cdot \hat{n} \delta t da}{\delta t} \\ & =N q \vec{v} \cdot \hat{n} da \end{aligned} \end{equation} 여기서 여러 종류의 전하가 있을 수 있으므로, 전하종류에 따른 고려를 하여 다음과 같이 쓸 수 있다. $$ d I=\left[\sum_i N_i q_i \vec{v}_i\right] \cdot \hat{n} da $$ 단위 면적당 전류를 전류밀도($\vec{J}$)라고 다음과 같이 정의하며, $$ dI=\vec{J} \cdot \hat{n} d a, $$ 다음과 같이 얻어진다. $$ \vec{J}=\sum_i N_i q_i \vec{v}_i $$ 전류밀도는 전류와는 달리 벡터량이다. 그러면 면 $S$를 통과하는 전류는 다음과 같이 얻어진다. $$ I=\int_S \vec{J} \cdot \hat{n} d a $$

6.2 연속 방정식

폐곡면 $S$로 출입하는 전류와 그 속에서 생성 소멸하는 전하밀도($\rho$) 사이의 관계를 얻어보자. 폐곡면 $S$로 전류 $I$가 들어오면, 전류 $I$는 다음과 같이 주어진다. $$ I=-\oint_S \vec{J} \cdot \hat{n} d a = -\int_{V} \nabla \cdot \vec{J} d v $$ 위 식은 divergence 정리가 적용되었다. $$ I=\frac{d Q}{d t}=\frac{d}{d t} \int_V \rho d v =\int_V \frac{\partial \rho}{\partial t} d v $$ 위 식을 이용하면, 다음이 주어진다. $$ \int_V\left(\frac{\partial \rho}{\partial t}+\nabla \cdot \vec{J}\right) d v=0 $$ 위 식으로 부터 다음이 성립한다. \begin{equation} \frac{\partial \rho}{\partial t}+\nabla \cdot J=0 \end{equation} 위 식을 연속방정식(continuous equation)이라고 한다.

6.3 Ohm의 법칙

온도가 일정한 금속에서 전류밀도는 전기장에 비례하며, 이것은 다음과 같이 기술될 수 있다. $$ \vec{J} = g(\vec{E}) \vec{E}, $$ 여기서 비례 계수 $g(\vec{E})$를 전도율(conductivity)이라고 하며, 일반적으로 전기장의 함수이다. 전류밀도가 전기장에 선형적으로 증가할 경우에는 전도율은 전기장에 무관하게 주어진다. $$ \vec{J}=g \vec{E} $$ 이 식을 Ohm의 법칙이라고 한다.
전도율(conductivity)의 역수인 $\eta$를 비저항(registivity)이라고 한다. $$ \eta=\frac{1}{g} $$ \begin{array}{lcc} \text { Material } & \eta, \Omega \mathrm{m} & \alpha=\frac{1}{\eta} \frac{d \eta}{d T},\left({ }^{\circ} \mathrm{C}\right)^{-1} \\ \hline \text { Aluminum } & 2.65 \times 10^{-8} & 0.0043 \\ \text { Copper } & 1.67 \times 10^{-8} & 0.0068 \\ \text { Gold } & 2.35 \times 10^{-8} & 0.004 \\ \text { Iron } & 9.71 \times 10^{-8} & 0.0065 \\ \text { Nickel } & 6.84 \times 10^{-8} & 0.0069 \\ \text { Silver } & 1.59 \times 10^{-8} & 0.0041 \\ \text { Mercury } & 95.8 \times 10^{-8} & 0.0009 \\ \text { Tungsten } & 5.51 \times 10^{-8} & 0.0045 \\ \text { Constantin (Cu 60, Ni } 40 \text { ) } & 49.0 \times 10^{-8} & 0.0000 \\ \text { Nichrome } & 100.0 \times 10^{-8} & 0.0004 \\ \text { Germanium (pure) } & 0.46 & -0.048 \\ \text { Germanium (5 } \left.10^{-6} \% \mathrm{As}\right) & 0.011 & \\ \text { Graphite } & 1.4 \times 10^{-5} & \\ \text { NaCl Solution (saturated) } & 0.044 & \\ \text { Aluminum oxide } & 1 & \\ \text { Glass } & 10^{10}-10^{14} & \\ \text { lodine } & 1.3 \times 10^{14} & \\ \text { Quartz (SiO }{ }_2 \text { ) } & 1 & \\ \text { Sulfur } & 2 & \\ \text { Wood } & 10^8-10^{11} & \\ \hline \end{array}

그림과 같이 길이 $l$인 도선 양단에 $\Delta \varphi$의 포텐셜차이가 있을 때, 전류를 $\Delta \varphi$로 표현할 수 있다. $\Delta \varphi$는 정의에 의해서 다음과 같이 주어진다. $$ \Delta \varphi=-\int \vec{E} \cdot d \vec{l} $$ 구간내에 전기장이 일정할때 위 식은 다음과 같이 된다. $$ \Delta \varphi=E l, $$ 전류는 다음과 같이 주어진다. $$ I=\int_A \vec{J} \cdot \hat{n} d a = J A= g E A = \frac{g A \Delta \varphi}{l}, $$ $$ \Delta \varphi = I \left( \frac{l}{g A} \right) = I \left( \frac{l \eta}{A} \right) $$ 여기서 $\frac{l \eta}{A}$을 저항(resistance) $R$이라고 정의하면, 다음과 같이 기술된다. $$ \Delta \varphi = I R $$ 이 식도 Ohm의 법칙이라고 한다. 저항의 단위는 $\Omega$ (Ohm)이라고 하고 다음의 차원을 갖는다. $$ 1 \mathrm{ohm}=\frac{1 \text { volt }}{1 \text { ampere }} $$ V($volt$)는 포텐셜의 단위이다.
시간 $dt$동안 $dQ$의 전하를 도선 한끝에서 다른 끝으로 이동시키는데 전기장이 한 일은 다음과 같이 주어지므로 $$ dW = dQ(\varphi_2-\varphi_1) $$ 전력(power)은 다음과 같이 정의 된다. $$ P = \frac{dW}{dt} = I \Delta \varphi=I^2 R=(\Delta \varphi)^2 / R $$ $\Delta \varphi$를 $V$로 쓰면, $$ P = \frac{dW}{dt} = I V =I^2 R = V^2 / R $$

6.4 직류 회로

• 저항의 연결

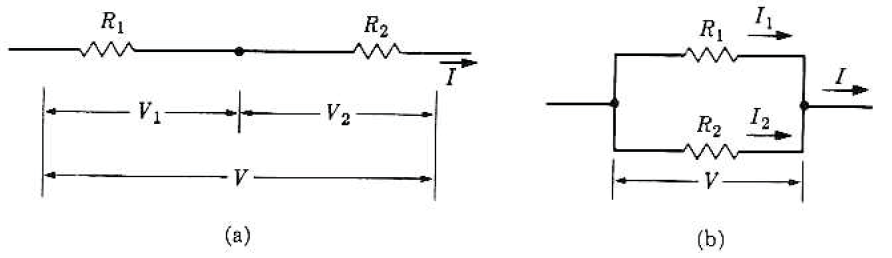
직렬 연결
전류가 공통, 전압이 갈라짐
$$ V = R_1 I + R_2 I=\left(R_1+R_2\right) I $$ $$ R=R_1+R_2 $$ 병렬 연결
전압이 공통, 전류가 갈라짐
$$ I=\frac{1}{R_1} V+\frac{1}{R_2} V=\left(\frac{1}{R_1}+\frac{1}{R_2}\right) V $$ $$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$$ • Kirchhoff의 법칙
Kirchhoff의 법칙은 다음의 두 가지로 요약된다.
1. 분기점을 향해 흐르는 전류의 대수적 합은 0이다.
$$ \sum I_j=0 . $$ 2. 회로의 모든 루프의 전압 차이의 대수적 합은 0이다.
$$ \sum V_j=0 . $$ 첫번째 법칙은 연속 방정식에서 정상 전류 조건인 다음식으로 부터 얻어지고 $$ \nabla \cdot \vec{J} = 0 $$ 두번째 법칙은 전기장이 보존장이라는 다음 조건에서 얻어진다. \begin{equation} \oint \vec{E} \cdot d \vec{l} = 0 \end{equation}

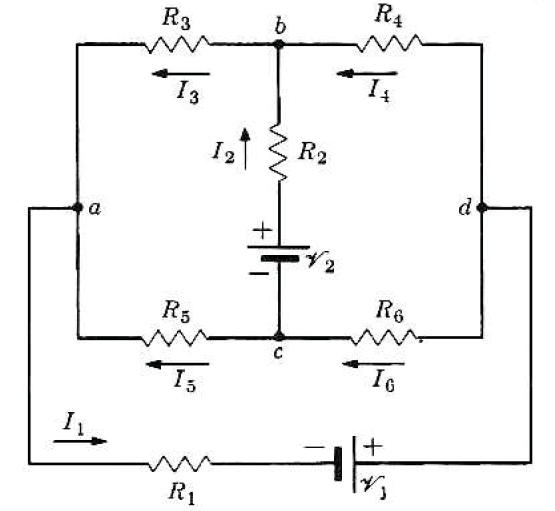
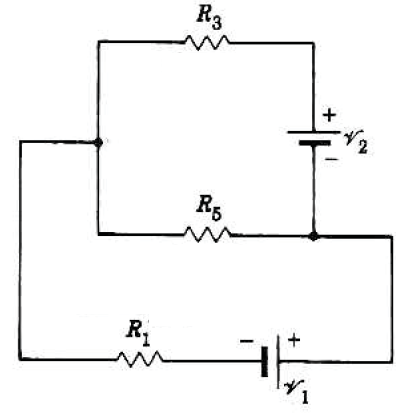
\begin{equation} \begin{aligned} & I_3+I_5-I_1=0 \\ & V_1=I_1 R_1+I_5 R_5 \\ & V_2=I_3 R_3-I_5 R_5 \end{aligned} \end{equation} $n$개의 방정식중에서 $n-1$개의 방정식만 독립적이다.