7. PN 접합(The PN junction)
7.1 PN 접합의 기본구조
 |
 |
• P형 반도체와 N형 반도체의 금속학적 접합
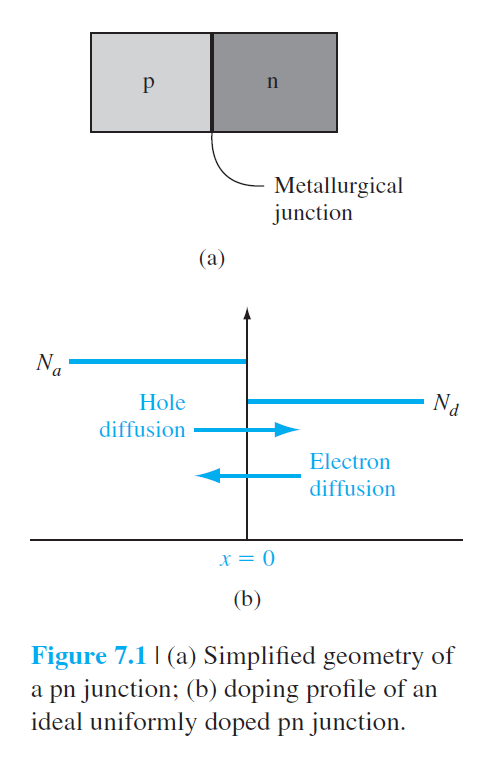
P형 반도체와 N형 반도체를 금속학적으로 접합(Metallurgical junction)시키자.
P형 반도체는 $N_a$의 도핑농도를 N형 반도체는 $N_d$의 도핑농도를 가지고 접합되어있는 것을 그린 7.1(a)가 잘 나타내고 있다.
이렇게 도핑농도가 갑작스럽게 변하는 것을 계단 접합(step junction)이라고 부를 수 있다.
• PN 접합에서 평형이 형성되는 과정
N영역내의 다수 운반자인 전자는 P영역으로 확산해 나간다.
유사하게 P영역내의 다수 운반자인 홀은 N영역으로 확산해 나간다.
이러한 확산과정은 무한히 지속될수는 없다.
왜냐하면 N영역내의 있던 전자가 P영역으로 떠나게 되면 전자가 떠난 N영역은 양($+$)의 전하를 띄게 되고
P영역내의 있던 홀이 N영역으로 떠나게 되면 홀이 떠난 P영역은 음($-$)의 전하를 띄게 되어,
N영역에서 P영역 방향으로 전기장이 발생하게 된다.
이 전기장은 전자와 홀의 확산을 억제하게 되는데, 적절한 선에서 그 확산과 전기장이 균형을 이루게 된다.
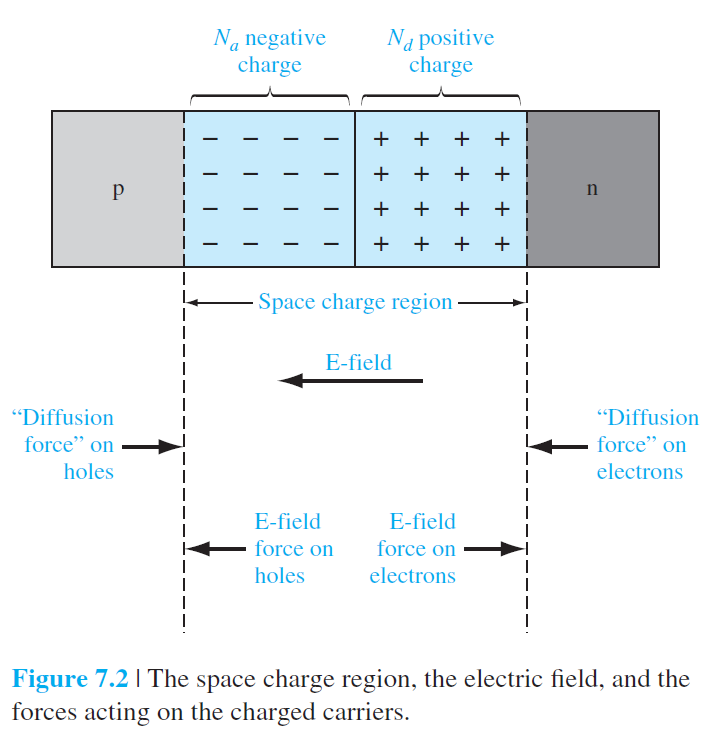
전자와 홀이 떠나서 극성을 띄게되는 영역을 Space charge region(공간전하영역) 또는 depletion region(공핍영역)이라고 한다.
공핍영역의 양끝단에는 아직 이동하지 않은 다수 운반자가 건재하기 때문에
이 양끝단에는 다수 운반자가 확산해 들어오려는 확산력이 있다고 볼수있다.
이러한 상황들을 그림 7.2(b)에서 잘보여주고 있다.
7.2 0 전압
먼저 인가 bias가 없는 경우에 PN 접합을 논의한다.
다음 두가지 가정하에 기술한다.
• Boltzmann 근사
Femi-Dirac 분포가 아닌 Boltzmann 근사를 사용한다.
이것은 degenerate되지 않은 반도체를 가정함을 의미한다.
• 완전이온화
편리한 기술을 위해 완전이온화를 가정한다.
일반적으로 상온(300 K)에서의 반도체는 종종 이 조건이 무난하게 달성된다.
7.2.1 Built-in 포텐셜 장벽(Built-in potential barrier)
P형 반도체에서는 Fermi 준위가 valence 밴드에 가깝고,
N형 반도체에서는 Fermi 준위가 conduction 밴드에 가깝다.
이 두 반도체를 접합하게 되면, Fermi 준위가 전체에 걸쳐서 동일한 수준을 유지해야하기 때문에,
그림 7.3처럼 conduction 밴드, valence 밴드, intrinsic 밴드들이 휘어지게 된다.
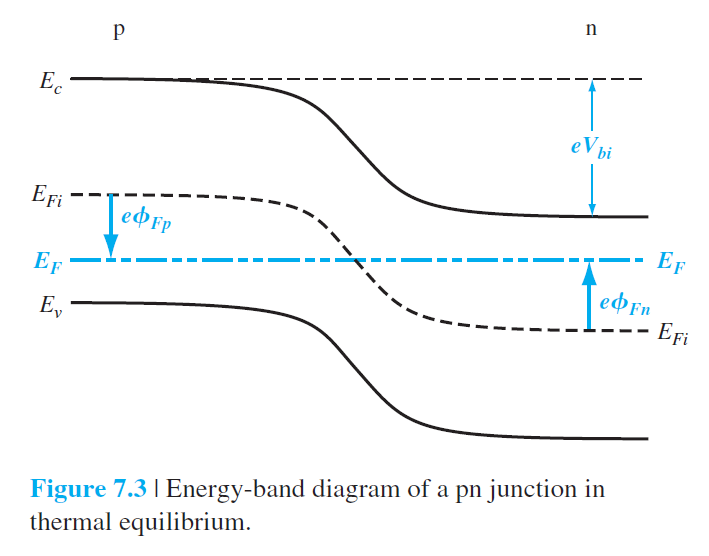
이러한 밴드들의 휘어짐은 전자가 N영역에서 P영역으로 이동할때 포텐셜장벽으로 작용한다.
이렇게 P와 N법합사이에 자연스럽게 발생하는 포텐셜 장벽을 Built-in 포텐셜 장벽(Built-in potential barrier)이라고 한다.
Built-in 포텐셜($V_{b i}$)은 다음과 같이 얻어질 수 있다.
$$ V_{b i}=\left|\phi_{F n}\right|+\left|\phi_{F p}\right| \qquad (7.1) $$
$\phi_{F n}$과 $\phi_{F p}$은 아래 (7.3)과 (7.7)식으로부터 얻어질 수 있다.
$$
n_0=n_i \exp \left[\frac{E_F-E_{F i}}{k T}\right] \qquad (7.3) $$
$$ e \phi_{F n}=E_{F i}-E_F \qquad (7.4) $$
$$ n_0=n_i \exp \left[\frac{-\left(e \phi_{F n}\right)}{k T}\right] \qquad (7.5) $$
$$ \phi_{F n}=\frac{-k T}{e} \ln \left(\frac{N_d}{n_i}\right) \qquad (7.6) $$
$$ p_0=N_a=n_i \exp \left[\frac{E_{F i}-E_F}{k T}\right] \qquad (7.7) $$
$$ e \phi_{F p}=E_{F i}-E_F \qquad (7.8) $$
$$ \phi_{F p}=+\frac{k T}{e} \ln \left(\frac{N_a}{n_i}\right) \qquad (7.9) $$
결과적으로 $V_{b i}$는 (7.6)식과 (7.9)으로부터 다음과 같이 얻어진다.
$$ V_{b i}=\frac{k T}{e} \ln \left(\frac{N_a N_d}{n_i^2}\right)=V_t \ln \left(\frac{N_a N_d}{n_i^2}\right) \qquad (7.10) $$
여기서 $V_t=kT/e$는 열전압(thermal voltage)이라고 부른다.

7.2.2 전기장
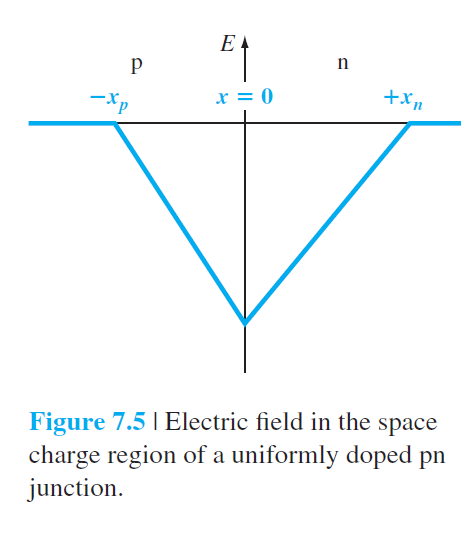
접합내에 전기장을 구해보면 동작을 이해하는데 도움이 된다.
전기장은 아래 Poisson 방정식을 이용하여 구할 수 있다.
$$ \nabla \phi(x) = -\frac{\rho(x)}{\epsilon_s} $$
여기서 $\epsilon_s$는 반도체의 유전율이다. 1 차원에 대해서 Poisson 방정식은 아래와 같이 쓸수있다.
$$ \frac{d^2 \phi(x)}{d x^2}=\frac{-\rho(x)}{\epsilon_s}=-\frac{d E(x)}{d x} \qquad (7.11) $$
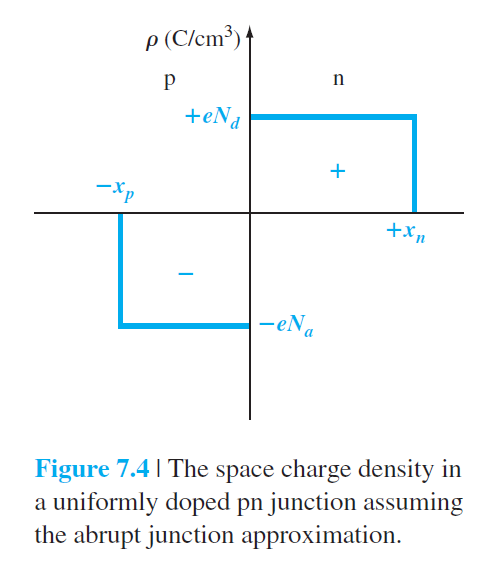
계산의 용이함을 위하여 $\rho(x)$가 다음과 같이 계단식으로 주어진다고 가정한다.
$$
\begin{aligned}
\rho(x) & = -e N_a \quad-x_p < x < 0 \qquad (7.12a) \\
\rho(x) & = e N_d \quad 0 < x < x_n \qquad (7.12b)
\end{aligned}
$$
$$
E=\int \frac{\rho(x)}{\epsilon_s} d x=-\int \frac{e N_a}{\epsilon_s} d x=\frac{-e N_a}{\epsilon_s} x+C_1 \qquad (7.13)
$$
$$
E=\frac{-e N_a}{\epsilon_s}\left(x+x_p\right) \quad-x_p \leq x \leq 0 \qquad (7.14)
$$
$$
E=\int \frac{\left(e N_d\right)}{\epsilon_s} d x=\frac{e N_d}{\epsilon_s} x+C_2 \qquad (7.15)
$$
$$
E=\frac{-e N_d}{\epsilon_s}\left(x_n-x\right) \quad 0 \leq x \leq x_n \qquad (7.16)
$$
$x = 0$에서 전기장 값이 연속이라는 조건으로부터 다음 식을 얻는다.
$$
N_a x_p=N_d x_n \qquad (7.17)
$$
이 식은 다음을 의미한다.
(단위면적당 음전하의 수)p 영역 = (단위면적당 음전하의 수)n 영역
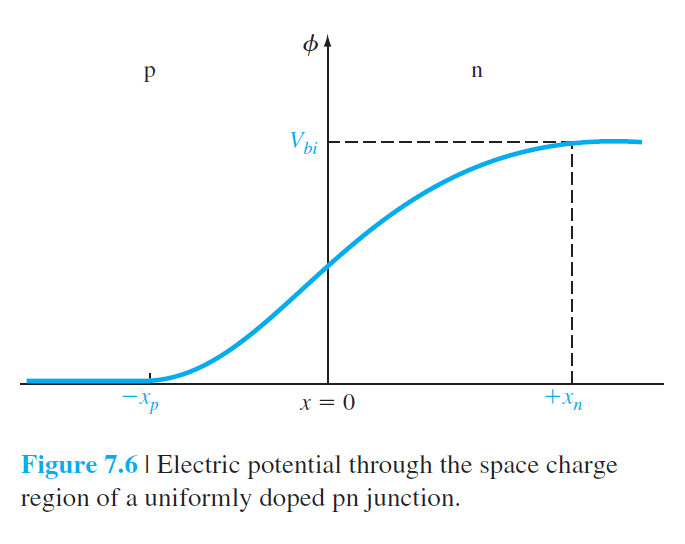
전기장을 적분하여 포텐셜을 얻을 수 있다.
$$
\phi(x)=-\int E(x) d x=\int \frac{e N_a}{\epsilon_s}\left(x+x_p\right) d x \qquad (7.18)
$$
$$
\phi(x)=\frac{e N_a}{\epsilon_s}\left(\frac{x^2}{2}+x_p \cdot x\right)+C_1' \qquad (7.19)
$$
$x=-x_p$에서 $\phi(x)=0$으로 기준을 정하면, 적분상수 $C_1'$은 다음과 같이 주어진다.
$$
C_1'=\frac{e N_a}{2 \epsilon_s} x_p^2 \qquad (7.20)
$$
그러면 P영역내의 포텐셜은 다음과 같이 주어진다.
$$
\phi(x)=\frac{e N_a}{2 \epsilon_s}\left(x+x_p\right)^2 \quad\left(-x_p \leq x \leq 0\right) \qquad (7.21)
$$
N영역내에서의 포텐셜은 다음과 같이 주어진다.
$$
\begin{aligned}
\phi(x)&=\int \frac{e N_d}{\epsilon_s}\left(x_n-x\right) d x \qquad (7.22) \\
\phi(x)&=\frac{e N_d}{\epsilon_s}\left(x_n \cdot x-\frac{x^2}{2}\right)+C_2' \qquad (7.23)
\end{aligned}
$$
$x=0$에서 포텐셜이 연속이라는 조건에서 적분상수 $C_2'$은 다음과 같이 주어진다.
$$
C_2'=\frac{e N_a}{2 \epsilon_s} x_p^2 \qquad (7.24)
$$
그러면 N영역내의 포텐셜은 다음과 같이 주어진다.
$$
\phi(x)=\frac{e N_d}{\epsilon_s}\left(x_n \cdot x-\frac{x^2}{2}\right)+\frac{e N_a}{2 \epsilon_s} x_p^2 \quad\left(0 \leq x \leq x_n\right) \qquad (7.25)
$$
$x=-x_p$에서 $\phi(x)=0$이므로 $x=x_n$에서 포텐셜이 $V_{bi}$를 결정한다고 볼수있다.
$$
V_{b i}=\left|\phi\left(x=x_n\right)\right|=\frac{e}{2 \epsilon_s}\left(N_d x_n^2+N_a x_p^2\right) \qquad (7.26)
$$
7.2.3 공핍층의 폭
(7.17)식으로 부터 다음 식을 얻는다.
$$ x_p=\frac{N_d x_n}{N_a} \qquad (7.27) $$
위 식을 (7.26)에 대입하여 $x_n$에 대해 풀면 다음을 얻는다.
$$
x_n=\sqrt{\frac{2 \epsilon_s V_{b i}}{e}\left(\frac{N_a}{N_d}\right)\frac{1}{N_a+N_d}} \qquad (7.28)
$$
$$
x_p=\sqrt{\frac{2 \epsilon_s V_{b i}}{e}\left(\frac{N_d}{N_a}\right)\frac{1}{N_a+N_d}} \qquad (7.29)
$$
공핍층의 폭 $W$는 다음과 같이 주어진다.
$$
W=x_n+x_p \qquad (7.30)
$$
$$
W = \sqrt{\frac{2 \epsilon_s V_{b i}}{e} \frac{N_a+N_d}{N_a N_d} } \qquad (7.31)
$$

7.3 역 전압
$$
V_{\text {total }}=\left|\phi_{F n}\right|+\left|\phi_{F p}\right|+V_R \qquad (7.32)
$$
$$
V_{\text {total }}=V_{b i}+V_R \qquad (7.33)
$$
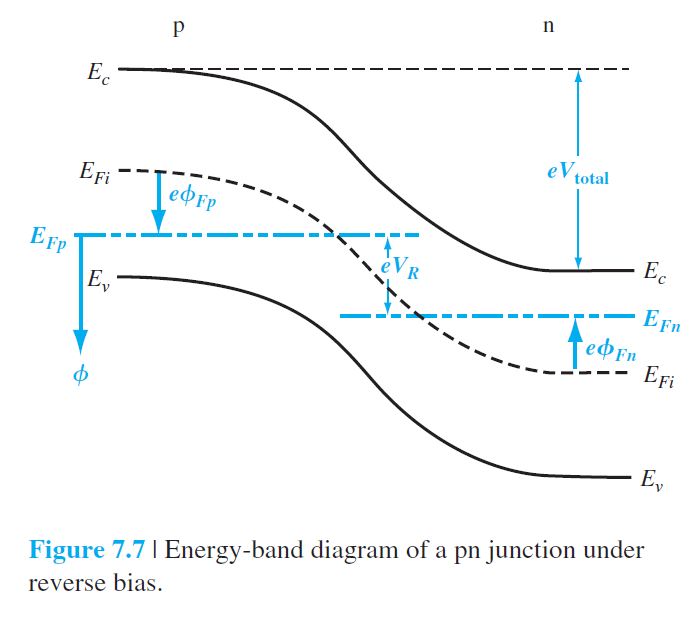
7.3.1 공핍층의 폭과 전기장
역전압에서 공핍층의 폭은 (7.31)식에서 $V_{b i}$를 $V_{bi}+V_R$로 대체하여 얻어진다.
\begin{equation}
W=\sqrt{\frac{2 \epsilon_s\left(V_{b i}+V_R\right)}{e} \frac{N_a+N_d}{N_a N_d} } \qquad (7.34)
\end{equation}
전기장의 최대값 $E_{\max}$는 (7.14)식과 (7.16)식에서 $x=0$으로 둠으로써 다음과 같이 주어진다.
$$ E_{\max } = \frac{-e N_d x_n}{\epsilon_s}=\frac{-e N_a x_p}{\epsilon_s} \qquad (7.35) $$
$$
E_{\max } = -\sqrt{\frac{2 e\left(V_{b i}+V_R\right)}{\epsilon_s} \frac{N_a N_d}{N_a+N_d} } \qquad (7.36)
$$
(7.34)식을 이용하면, $E_{\max}$는 다음과 같이 간단히 주어진다.
$$
E_{\max}=\frac{-2\left(V_{b i}+V_R\right)}{W} \qquad (7.37)
$$
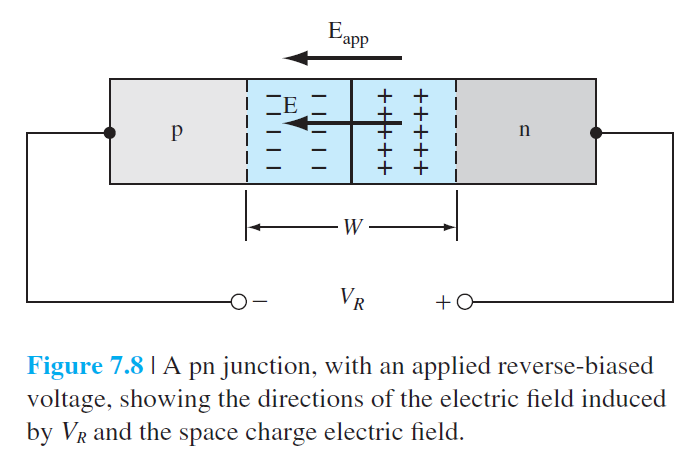


7.3.2 접합 전기용량(Junction capacitance)
PN 접합내에서 양의 전하와 음의 전하를 포함하고있기 때문에, 전기용량(capacitance)을 정의할 수 있다.
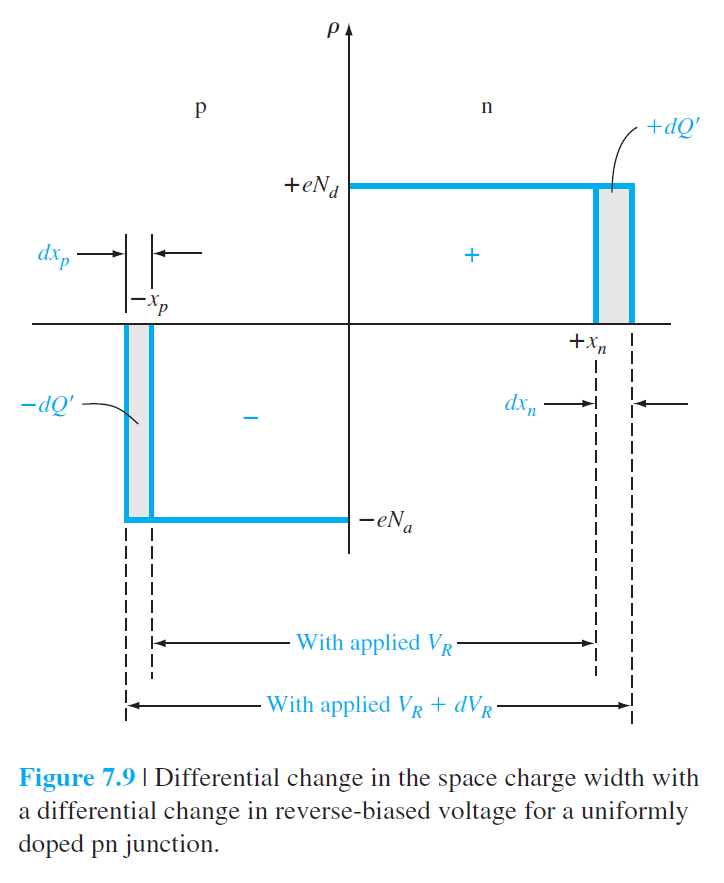
역바이어스가 $d V_R$ 만큼 증가하는 동안 $d Q'$ 만큼 전하가 증가한다면 단위 면적당 전기용량 $C'$은 다음과 같이 주어진다.
$$ C'=\frac{d Q'}{d V_R} \qquad (7.38) $$
여기서 따옴표(')는 단위 면적당을 표시한다.
즉
$$ \frac{C}{A}=\frac{d Q}{d (A V_R)} \rightarrow C'=\frac{d Q'}{d V_R} $$
여기서 $C/A=C'$, $Q'=Q/A$로 두고, $A$는 면적이다.
$d Q'$은 다음과 같이 주어진다.
$$ d Q'=e N_d d x_n=e N_a d x_p \qquad (7.39)$$
$x_n$이 다음과 같이 주어진다는 것을 고려하면,
$$
x_n=\sqrt{\frac{2 \epsilon_s\left(V_{b i}+V_R\right)}{e}\left(\frac{N_a}{N_d}\right) \frac{1}{N_a+N_d} } \qquad (7.40)
$$
$C'$는 다음과 같이 주어진다.
$$
C'=\frac{d Q'}{d V_R}=e N_d \frac{d x_n}{d V_R} \qquad (7.41)
$$
$$
C' = \sqrt{\frac{e \epsilon_s N_a N_d}{2\left(V_{b i}+V_R\right)\left(N_a+N_d\right)} } \qquad (7.42)
$$
(7.34)식을 이용하면, $C'$는 다음과 같이 주어진다.
$$
C'=\frac{\epsilon_s}{W} \qquad (7.43)
$$
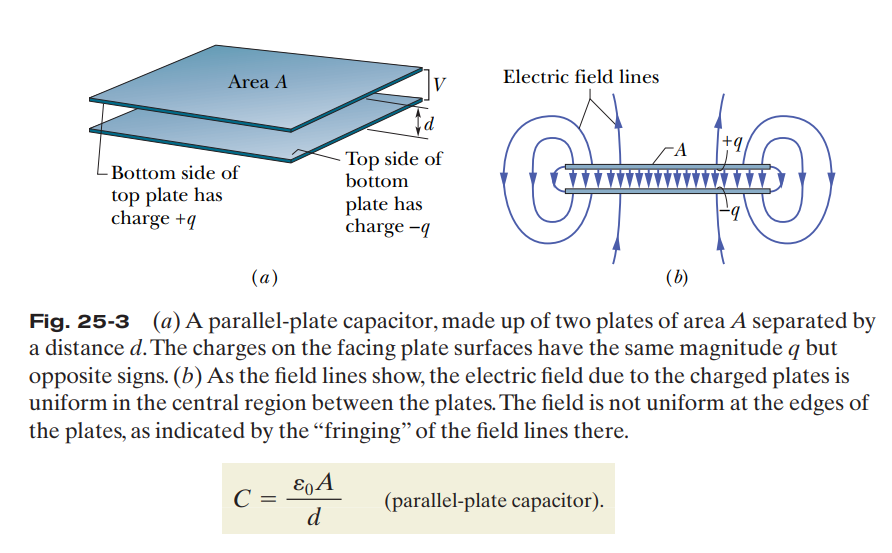
결과적으로 거리 $d$만큼 떨어진 두 나란한 평판으로 이루어진 축전기의 전기용량과 동일함을 알수있다.
접합 전기용량(junction capacitance)은 공핍층 전기용량(depletion layer capacitance)이라고도 한다.

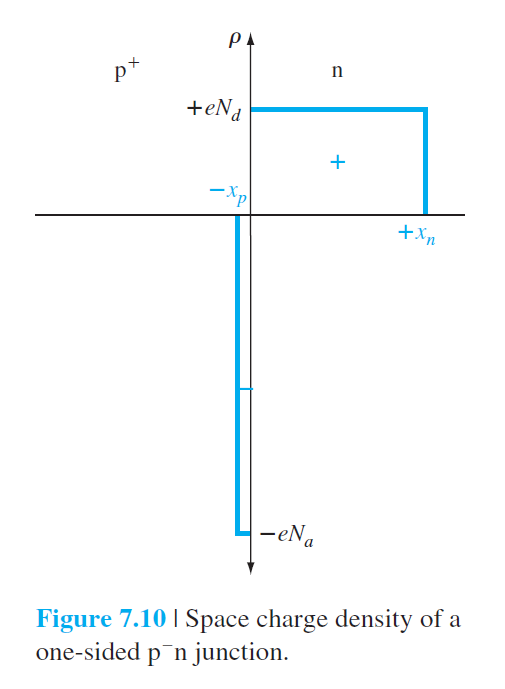
7.3.3 일방 접합(One-sided junctions)
P영역의 도핑농도가 N영역의 도핑농도보다 월등히 큰 경우를 생각해보자. ($N_a\gg N_d$)
(7.34)식으로부터
$$
W \approx\sqrt{\frac{2 \epsilon_s\left(V_{b i}+V_R\right)}{e N_d} } \qquad (7.44)
$$
$$x_p \ll x_n \qquad (7.45)$$
$$W \approx x_n \qquad (7.46)$$
(7.42)식으로부터
$$
C' \approx\sqrt{\frac{e \epsilon_s N_d}{2\left(V_{b i}+V_R\right)} } \qquad (7.47)
$$
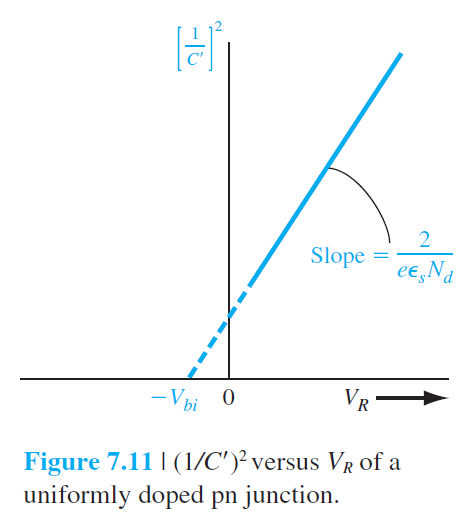
$$
\left(\frac{1}{C'}\right)^2=\frac{2\left(V_{b i}+V_R\right)}{e \epsilon_s N_d} \qquad (7.48)
$$

7.4 접합 항복
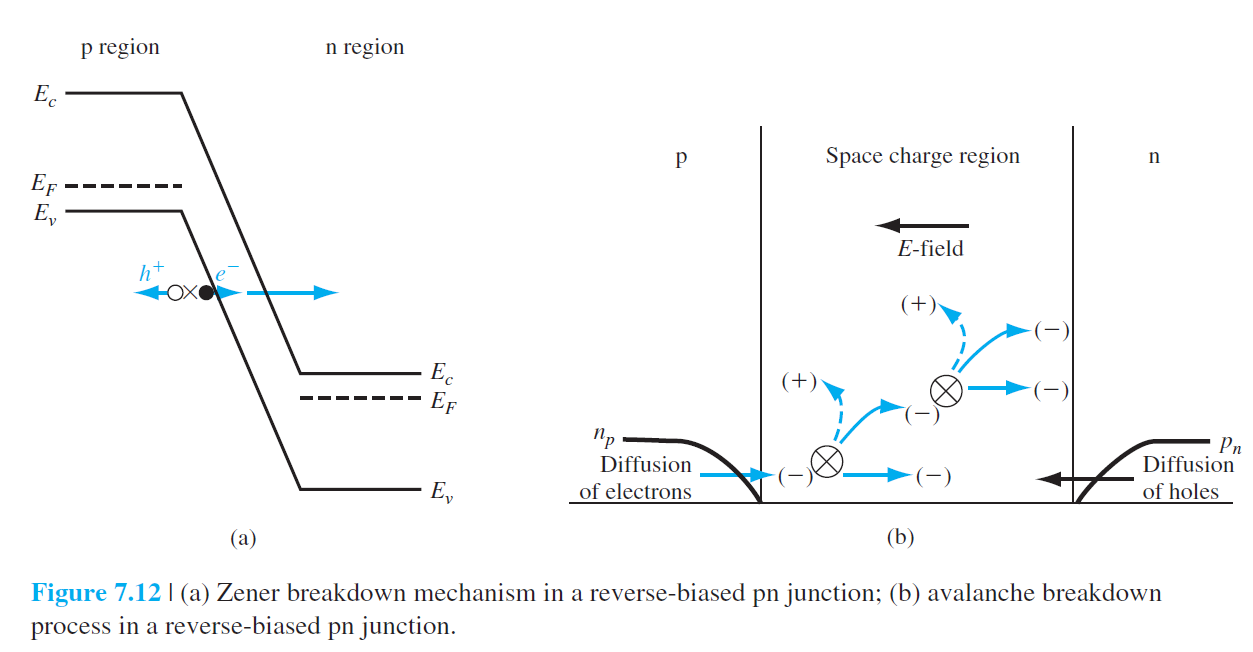 역전압을 과도하게 가하다 보면 접합 항복(junction breakdown)이 발생할 수 있다.
접합 항복이 발생하는 대표적인 메커니즘은 Zener 효과와 avalanche 효과가 있다.
접합 항복이 일어나는 전압을 항복전압(breakdown voltage)이라고 한다.
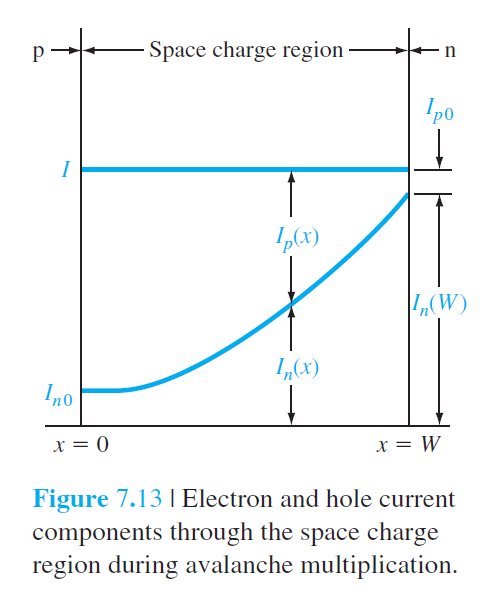
\begin{equation}
I_n(W)=M_n I_{n 0} \qquad (7.49)
\end{equation}
$$
d I_n(x)=I_n(x) \alpha_n d x+I_p(x) \alpha_p d x
$$
$$
\frac{d I_n(x)}{d x}=I_n(x) \alpha_n+I_p(x) \alpha_p
$$
$$
I=I_n(x)+I_p(x)
$$
$$
\frac{d I_n(x)}{d x}+\left(\alpha_p-\alpha_n\right) I_n(x)=\alpha_p I
$$
$$
\alpha_n=\alpha_p \equiv \alpha
$$
$$
I_n(W)-I_n(0)=I \int_0^W \alpha d x
$$
$$
\frac{M_n I_{n 0}-I_n(0)}{I}=\int_0^W \alpha d x
$$
$$
1-\frac{1}{M_n}=\int_0^W \alpha d x
$$
$$
\int_0^W \alpha d x=1
$$
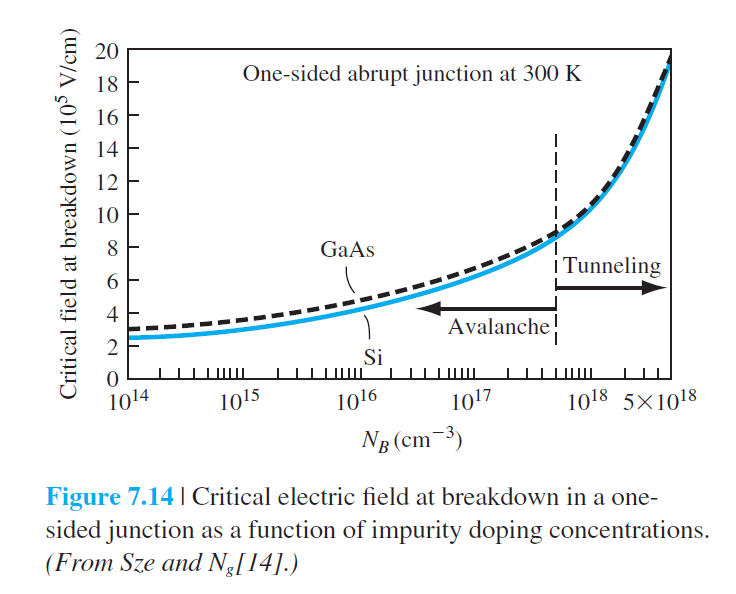
$p^+n$ 일방접합에 대해서 $E_{\max}$는 (7.35)식으로부터 다음과 같이 주어진다.
$$
E_{\max }=\frac{e N_d x_n}{\epsilon_s} \qquad (7.59)
$$
$p^+n$ 일방접합에 대해서 $x_n$은 (7.44)식으로부터 다음과 같이 주어진다.
$$
x_n \approx\sqrt{\frac{2 \epsilon_s V_R}{e} \cdot \frac{1}{N_d} } \qquad (7.60)
$$
여기서 $V_{bi}$는 무시되었다.
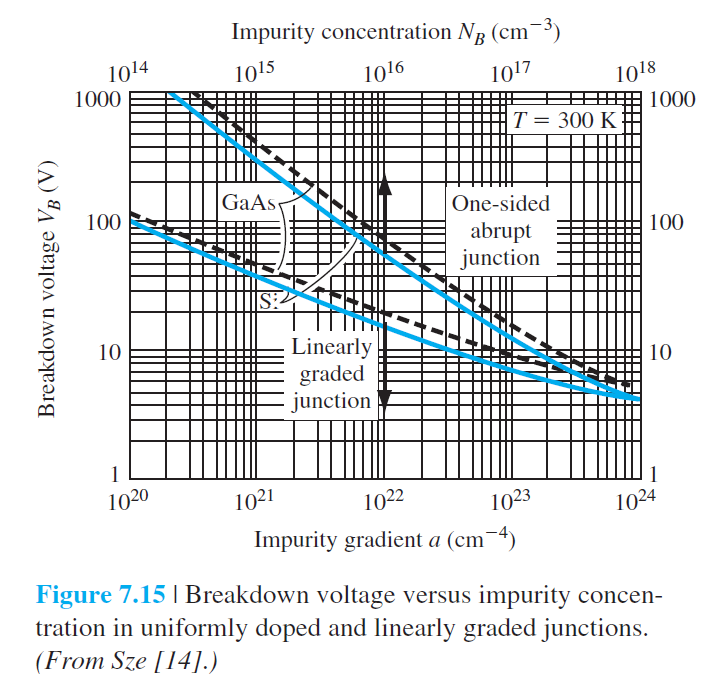
항복(breakdown)이 일어나는 역전압을 $V_B$이라고 두면,
$$
V_B=\frac{\epsilon_s E_{\text {임계}}^2}{2 e N_B} \qquad (7.61)
$$
여기서 $E_{\text {임계}}$는 항복이 일어날 때의 $E_{\max }$이다.
$N_B$ 일방 접합에서 저농도 도핑영역의 도핑농도 $N_d$이다.
역전압을 과도하게 가하다 보면 접합 항복(junction breakdown)이 발생할 수 있다.
접합 항복이 발생하는 대표적인 메커니즘은 Zener 효과와 avalanche 효과가 있다.
접합 항복이 일어나는 전압을 항복전압(breakdown voltage)이라고 한다.
\begin{equation}
I_n(W)=M_n I_{n 0} \qquad (7.49)
\end{equation}
$$
d I_n(x)=I_n(x) \alpha_n d x+I_p(x) \alpha_p d x
$$
$$
\frac{d I_n(x)}{d x}=I_n(x) \alpha_n+I_p(x) \alpha_p
$$
$$
I=I_n(x)+I_p(x)
$$
$$
\frac{d I_n(x)}{d x}+\left(\alpha_p-\alpha_n\right) I_n(x)=\alpha_p I
$$
$$
\alpha_n=\alpha_p \equiv \alpha
$$
$$
I_n(W)-I_n(0)=I \int_0^W \alpha d x
$$
$$
\frac{M_n I_{n 0}-I_n(0)}{I}=\int_0^W \alpha d x
$$
$$
1-\frac{1}{M_n}=\int_0^W \alpha d x
$$
$$
\int_0^W \alpha d x=1
$$
$p^+n$ 일방접합에 대해서 $E_{\max}$는 (7.35)식으로부터 다음과 같이 주어진다.
$$
E_{\max }=\frac{e N_d x_n}{\epsilon_s} \qquad (7.59)
$$
$p^+n$ 일방접합에 대해서 $x_n$은 (7.44)식으로부터 다음과 같이 주어진다.
$$
x_n \approx\sqrt{\frac{2 \epsilon_s V_R}{e} \cdot \frac{1}{N_d} } \qquad (7.60)
$$
여기서 $V_{bi}$는 무시되었다.
항복(breakdown)이 일어나는 역전압을 $V_B$이라고 두면,
$$
V_B=\frac{\epsilon_s E_{\text {임계}}^2}{2 e N_B} \qquad (7.61)
$$
여기서 $E_{\text {임계}}$는 항복이 일어날 때의 $E_{\max }$이다.
$N_B$ 일방 접합에서 저농도 도핑영역의 도핑농도 $N_d$이다.

7.5 불균일 도핑된 접합
$$ \rho(x)=e a x $$ $$ \frac{d E}{d x}=\frac{\rho(x)}{\epsilon_s}=\frac{e a x}{\epsilon_s} $$ $$ E=\int \frac{e a x}{\epsilon_s} d x=\frac{e a}{2 \epsilon_s}\left(x^2-x_0^2\right) $$ $$ \phi(x)=-\int E d x $$ $$ \phi(x)=\frac{-e a}{2 \epsilon_s}\left(\frac{x^3}{3}-x_0^2 x\right)+\frac{e a}{3 \epsilon_s} x_0^3 $$ $$ \phi\left(x_0\right)=\frac{2}{3} \cdot \frac{e a x_0^3}{\epsilon_s}=V_{b i} $$ $$ V_{b i}=V_t \ln \left[\frac{N_d\left(x_0\right) N_a\left(-x_0\right)}{n_i^2}\right] $$ $$ N_d\left(x_0\right)=a x_0 $$ $$ N_a\left(-x_0\right)=a x_0 $$ $$ V_{b i}=V_t \ln \left(\frac{a x_0}{n_i}\right)^2 $$ $$ x_0=\left\{\frac{3}{2} \cdot \frac{\epsilon_s}{e a}\left(V_{b i}+V_R\right)\right\}^{1 / 3} $$ $$ C'=\frac{d Q'}{d V_R}=\left(e a x_0\right) \frac{d x_0}{d V_R} $$ $$ C'=\left\{\frac{e a \epsilon_s^2}{12\left(V_{b i}+V_R\right)}\right\}^{1 / 3} $$ $$ N=B x^m $$ $$ C'=\left\{\frac{e B \epsilon_s^{(m+1)}}{(m+2)\left(V_{b i}+V_R\right)}\right\}^{1 /(m+2)} $$ $$ f_r=\frac{1}{2 \pi \sqrt{L C}} $$ $$ C=C_0\left(V_{b i}+V_R\right)^{-1 /(m+2)} $$ $$ C \alpha V^{-2} $$ $$ \begin{gathered} \frac{1}{m+2}=2 \\ m=-\frac{3}{2} \end{gathered} $$