7. 자기장
7.1 전류에 의한 자기장
• Biot - Savart의 법칙
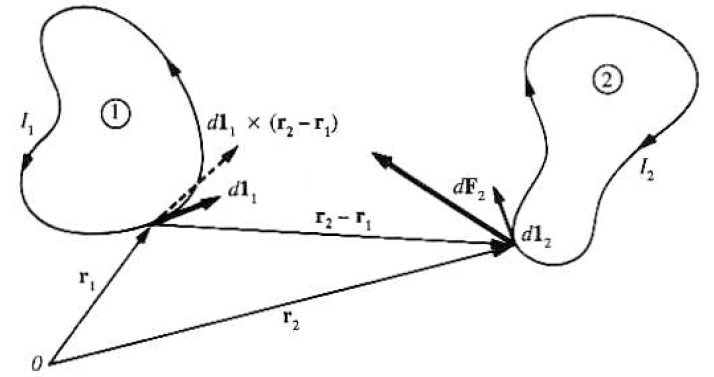
Ampere는 전류가 흐르는 두 회로사이의 힘에 관한 일련의 실험결과를 아래의 식(7-1)과 같이 정리했다.
그림과 같이 전류 $I_1$과 $I_2$가 각각 흐르는 두 회로 1과 2가 있으며,
회로2가 회로1로부터 받는 힘은 다음과 같이 표현된다.
$$
\vec{F}_2=\frac{\mu_0}{4 \pi} I_1 I_2 \oint_1 \oint_2
\frac{d \vec{\ell}_2 \times\left[d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)\right]}{\left|\vec{r}_2-\vec{r}_1\right|^3} \quad 식(7-1)
$$
여기서 $\mu_0$는 진공의 투자율(permeability)이라고 하며,
MKS 단위계로 다음과 같은 값으로 주어진다.
$$
\frac{\mu_0}{4 \pi}=10^{-7} \quad\mathrm{N} \cdot \mathrm{s}^2 / \mathrm{C}^2 =10^{-7} \quad\mathrm{N} / \mathrm{A}^2 \quad 식(7-2)
$$
참고로 $\mu_0$와 $\epsilon_0$는 다음과 같은 관계를 가진다.
$$
\epsilon_0 \mu_0=\frac{1}{c^2},
$$
$c$는 다음과 같이 주어지는 속도 차원의 값인데, 빛의 속도로 알려진다.
$$
c=2.9979 \times 10^8 \mathrm{~m} / \mathrm{s}
$$
다음과 같이 정의하면,
$$
\vec{B}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} I_1 \oint_1 \frac{d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} \quad 식(7-3)
$$
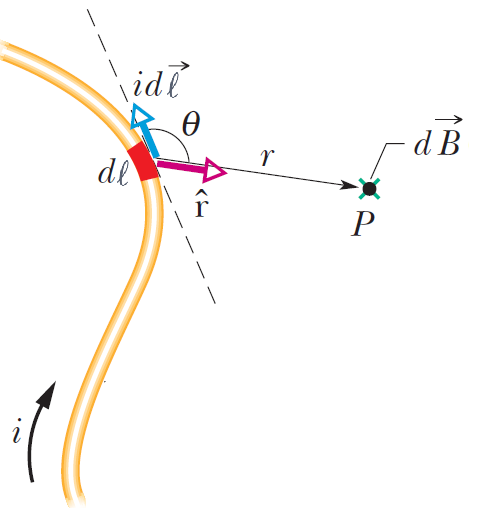
좀더 직관적인 이해를 돕기위해서 위 그림을 참고하자.
힘 $\vec{F}_2$는 다음과 같이 표현될 수 있다.
$$
\vec{F}_2= I_2 \oint_2 d \vec{\ell}_2 \times \vec{B}\left(\vec{r}_2\right) \quad 식(7-4)
$$
식(7-3)을 Biot - Savart의 법칙이라고 하며, $\vec{B}$는 전류 $I_1$이 만드는 자기유도(magnetic induction)라고 정의된다.
자기유도의 단위는 MKS단위계에서 T(tesla) CGS단위계에서 G(gauss)라고 한다.
식(7-4)를 일반화하여 다음과 같이 쓸수있다.
$$
\vec{F}= \oint_C I d \vec{\ell} \times \vec{B}\left(\vec{r}\right) \quad 식(7-5)
$$
식(7-5)는 자기유도 $\vec{B}(\vec{r})$가 있는 공간에서 전류 $I$가 흐르는 회로가 받는 힘으로 해석된다.
식(7-5)는 자기유도 $\vec{B}(\vec{r})$가 회로의 각 지점에 대해서 위치 의존성을 가진다고 가정되어 있다.
만약 회로내에 일정한 전류 $I$가 흐르고, 공간적으로 균일한 자기장이 가해진다면,
식(7-5)는 다음과 같이 기술될 수 있다.
$$
\vec{F}=I\left\{\oint_C d \vec{\ell}\right\} \times \vec{B} \quad 식(7-6)
$$
여기서 $\oint_C d \vec{\ell} =0$ 이기 때문에, 식(7-6)은 0이 된다.
$$
\vec{F}=\oint_C I d \vec{\ell} \times \vec{B}=0 \quad \text { (B 균일) } \quad 식(7-7)
$$
$\vec{B}$가 균일할 경우 폐회로가 받는 힘은 0이지만, 회전력(torque)은 존재한다.
전류고리가 자기장 $\vec{B}$로 부터 받는 회전력을 구해보자.
전류고리의 미소 길이 $d \vec{\ell}$가 받는 회전력은 다음과 같이 표현될 수 있다.
$$
d \vec{\tau}=\vec{r} \times d \vec{F}=I \vec{r} \times(d \vec{\ell} \times \vec{B}) .
$$
전류고리 전체가 받는 회전력은 다음과 같다.
다음 관계들을 이용하면,
$$
\vec{\tau} =I \oint_C \vec{r} \times(d \vec{\ell} \times \vec{B})
$$
$$
\begin{aligned}
&d \vec{\ell} \times \vec{B} \\
&=\hat{i}\left(d y B_z-d z B_y\right)+\hat{j}\left(d z B_x-d x B_z\right)+\hat{k}\left(d x B_y-d y B_x\right)
\end{aligned}
$$
$$
\begin{aligned}
& [\vec{r} \times(d \vec{\ell} \times \vec{B})]_x=y d x B_y-y d y B_x-z d z B_x+z d x B_z \\
& [\vec{r} \times(d \vec{\ell} \times \vec{B})]_y=z d y B_z-z d z B_y-x d x B_y+x d y B_x \\
& [\vec{r} \times(d \vec{\ell} \times \vec{B})]_z=x d z B_x-x d x B_z-y d y B_z+y d z B_y
\end{aligned}
$$
회전력은 다음과 같이 주어진다.
$$
\begin{aligned}
\tau_x &= I \int [\vec{r} \times(d \vec{\ell} \times \vec{B})]_x= A_y B_z - A_z B_y\\
\tau_y &= I \int [\vec{r} \times(d \vec{\ell} \times \vec{B})]_y= A_z B_x - A_x B_z\\
\tau_z &= I \int [\vec{r} \times(d \vec{\ell} \times \vec{B})]_z= A_x B_y - A_y B_x
\end{aligned}
$$
$$
\begin{aligned}
\tau_x &= I\left(A_y B_z-A_z B_y\right)\\
\tau_y &= I\left(A_z B_x-A_x B_z\right)\\
\tau_z &= I\left(A_x B_y-A_y B_x\right)
\end{aligned}
$$
$$
\vec{\tau}=I \vec{A} \times \vec{B} \quad \text { (B 균일) }
$$
7.2 자기쌍극자
• 전류고리의 자기쌍극자
면적 벡터 $\vec{A}$이고 전류 $I$가 흐르는 고리가 만는 자기 쌍극자 모먼트(magnetic dipole moment) $\vec{m}$은 다음과 같이 정의 된다.
$$
\vec{m}=I \vec{A},
$$
면적 벡터 $\vec{A}$의 크기는 면적 $A$이고, 방향은 전류가 흐르는 방향을 기준으로 오른손 법칙으로 정해진다.
$\vec{A}$를 다음과 같이 정의할수있다는 것을 고려하면,
$$
\vec{A} = \frac{1}{2} \oint_C \vec{r} \times d \vec{\ell}
$$
자기 쌍극자 모먼트는 다음과 같이 표현될 수 있다.
$$
\vec{m}=\frac{1}{2} I \oint_C \vec{r} \times d \vec{\ell}
$$
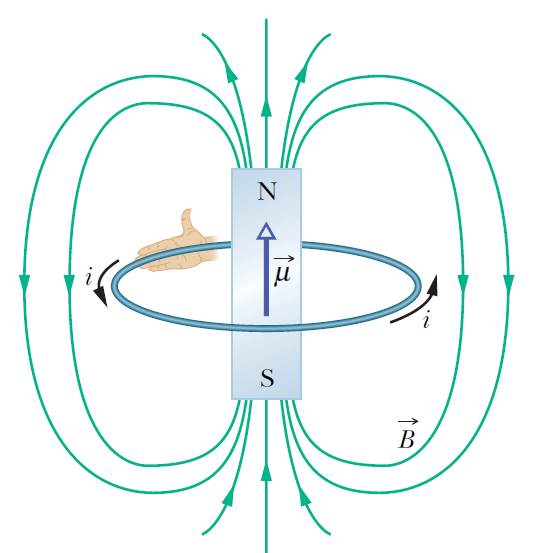
그림과 같이 자기 유도를 발생시키는 전류고리 주위에 N극과 S극을 정의할 수 있다.
$I d \vec{\ell} \rightarrow \vec{J} d v$ 이 치환을 이용하면,
자기 쌍극자 모먼트는 다음과 같이 전류밀도로 표현될 수 있다.
$$
\vec{m}=\frac{1}{2} \int_V \vec{r} \times \vec{J} d v_I,
$$
• 자기 쌍극자에 대한 회전력(torque)
식 ?은 균일한 자기장으로부터 전류고리가 받는 회전력인데
$\vec{m}=I \vec{A}$을 이용하여 자기 쌍극자 모먼트가 받는 힘을 도출할 수 있다.
$$
\vec{\tau}=\vec{m} \times \vec{B}
$$
• 자기홀극의 부재
자기쌍극자의 정의로 부터
$Id\vec{\ell}\rightarrow \vec{J} dv_1$로 치환하여
Biot - Savart의 법칙은 다음과 같이 전류밀도로 표현할 수 있다.
$$
\vec{B}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} \int_V \frac{\vec{J}\left(\vec{r}_1\right) \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \quad 식(7-6)
$$
다음 관계를 이용하면,
$$\nabla \cdot(\vec{F} \times \vec{G})= -\vec{F} \cdot \nabla \times \vec{G}+\vec{G} \cdot \nabla \times \vec{F}$$
$\vec{B}$의 divergence는 0이라는 것이 다음과 같이 증명된다.
$$\nabla \cdot \vec{B}=0 \quad 식(7-7)$$
(증명)
식(7-3)에 divergence를 취하면,
\begin{equation}
\begin{aligned}
\nabla_2 \cdot \vec{B}\left(\vec{r}_2\right)
& = \frac{\mu_0}{4 \pi} \oint_1 \nabla_2 \cdot \left( \frac{ \vec{J}(\vec{r}_1) \times(\vec{r}_2-\vec{r}_1)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1\right) \\
& = -\frac{\mu_0}{4 \pi} \int_V \vec{J}(\vec{r}_1) \cdot \nabla_2 \times \frac{\vec{r}_2-\vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \\
& = 0
\end{aligned}
\end{equation}
식(7-7)이 의미하는 것은 자기홀극은 0이라는 것을 의미한다.(Poisson 방정식과 비교)
이러한 이유로 자석은 N극과 S극이 항상 쌍으로 존재하지, 홀로 존재하지 않는다.
7.3 움직이는 전하에 의한 자기장
좀 더 본질적인 해석을 위해, 전류가 아닌 전하 하나가 자기유도로 부터 받는 힘을 도출할 수 있다.
식(7-5)는 회로 전체가 받는 힘이고, 회로의 극히 일부분이 받는 힘은 다음과 같이 표현될 수 있다.
\begin{equation}
\begin{aligned}
d\vec{F} & = Id\vec{\ell} \times \vec{B}\left(\vec{r}\right) \\
& = \vec{J} \times \vec{B}\left(\vec{r}\right) dv_I \\
& = Nq\vec{v} \times \vec{B}\left(\vec{r}\right) dv_I \quad 식(7-8)
\end{aligned}
\end{equation}
전류밀도 $\vec{J}$는 $Nq \vec{v}$ 로 쓸수있다.
여기서 $N$과 $\vec{v}$는 각각 단위 부피당 전하의 갯수 및 전하의 속도이다.
$dv_I$는 전류가 흐르는 영역의 부피이고,
$dv_I$를 전하 하나가 차지하는 부피로 제한하면($N dv_I=1$), 결과적으로 하나의 전하 $q$가 받는 힘은 다음과 같이 주어진다.
$$
\vec{F}_m = q \vec{v} \times \vec{B} \quad 식(7-9)
$$
여기서, 아래첨자 $m$은 자기유도로 부터 받는 힘이라는 것을 표시하기 위해서 붙여졌다.
이미 학습한 바와 같이 전하는 자기유도 외에 전기장으로 부터도 힘을 받는다.
공간상에 전기장과 자기유도 모두 존재할때 전하가 받는 힘은 다음과 같이 표현될 수 있다.
$$
\vec{F}=q(\vec{E}+\vec{v} \times \vec{B}) \quad 식(7-10)
$$
위 힘을 Lorents 힘이라고 한다.
참고로 식(7-6)으로부터, 전하 하나가 만드는 자기유도를 도출해 낼수 있다.
식(7-6)는 전류고리 전체가 만드는 자기유도이고,
전류고리에서 극히 미세한 부분이 만드는 자기 유도는 다음과 같다.
\begin{equation}
\begin{aligned}
d\vec{B}\left(\vec{r}_2\right)
& =\frac{\mu_0}{4 \pi} \frac{\vec{J}\left(\vec{r}_1\right) \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \\
& =\frac{\mu_0}{4 \pi} \frac{Nq\vec{v}\left(\vec{r}_1\right) \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \\
\end{aligned}
\end{equation}
$d v_1$를 전하 하나가 차지하는 부피로 제한하면($N d v_1 = 1$),
\begin{equation}
\begin{aligned}
d\vec{B}\left(\vec{r}_2\right)
& =\frac{\mu_0}{4 \pi} \frac{q\vec{v} \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} \\
\end{aligned}
\end{equation}
결과적으로 속도 $\vec{v}$로 움직이는 전하 $q$가 만드는 자기유도는 다음과 같다.
\begin{equation}
\begin{aligned}
\vec{B}_q(\vec{r}_2) =\frac{\mu_0}{4 \pi} \frac{q\vec{v} \times\vec{r}}{r^3}
\end{aligned}
\end{equation}
여기서 $\vec{r} = \vec{r}_2-\vec{r}_1$
7.4 Biot - Savart 법칙의 적용예
(예제1) 직선 도선주위의 자기장
전류 $I$가 흐르는 무한 도선 주위의 자기장을 구해보자.
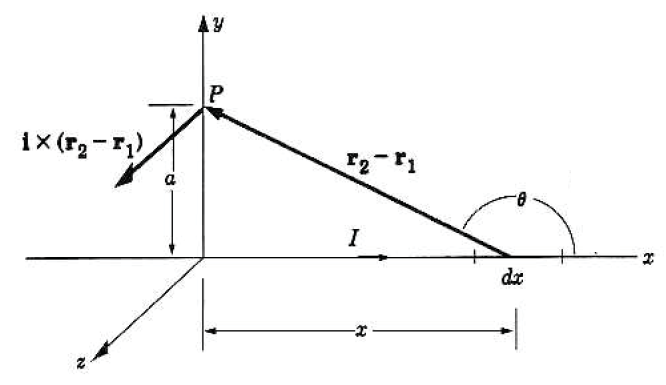
\begin{equation}
\begin{aligned}
\vec{B}\left(\vec{r}_2\right)&=\frac{\mu_0}{4 \pi} I_1 \oint_1 \frac{d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} \quad 식(7-3)\\
\vec{B}\left(\vec{r}_2\right)&=\frac{\mu_0}{4 \pi} I \int_{-\infty}^{\infty} \frac{d x \hat{i} \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3}
\end{aligned}
\end{equation}
$$
\hat{i} \times\left(\vec{r}_2-\vec{r}_1\right)=\left|\vec{r}_2-\vec{r}_1\right| \sin \theta \hat{k} .
$$
$$
\frac{a}{x}=\tan (\pi-\theta)=-\tan \theta
$$
$$
\left|\vec{r}_2-\vec{r}_1\right|=a \csc (\pi-\theta)=a \csc \theta .
$$
$$
\vec{B}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} I \hat{k} \frac{1}{a} \int_0^\pi \sin \theta d \theta=\left.\frac{\mu_0 I}{4 \pi a} \hat{k}(-\cos \theta)\right|_0 ^\pi=\frac{\mu_0 I}{2 \pi a} \hat{k} .
$$
(예제2) 도선 고리
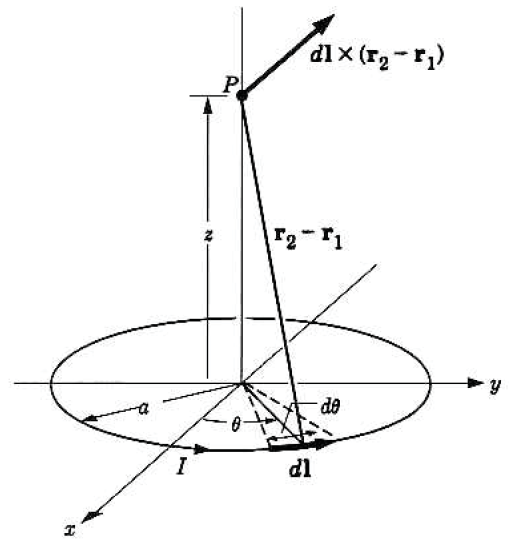
$$
\begin{aligned}
d \vec{\ell} & =a d \theta(-\hat{i} \sin \theta+\hat{j} \cos \theta) \\
\vec{r}_2-\vec{r}_1 & =-\hat{i} a \cos \theta-\hat{j} a \sin \theta+\hat{k} z \\
\left|\vec{r}_2-\vec{r}_1\right| & =\left(a^2+z^2\right)^{\mathbf{1 / 2}}
\end{aligned}
$$
$$
\begin{aligned}
\vec{B}(\vec{r}_2)&=\frac{\mu_0}{4 \pi} I_1 \oint_1 \frac{d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} \quad 식(7-3)\\
\vec{B}(z)&=\frac{\mu_0 I}{4 \pi} \int_0^{2 \pi} \frac{\left(\hat{i} z a \cos \theta+\hat{j} z a \sin \theta+\hat{k} a^2\right)}{\left(z^2+a^2\right)^{3 / 2}} d \theta .
\end{aligned}
$$
$$
\vec{B}(z)=\frac{\mu_0 I}{2} \frac{a^2}{\left(z^2+a^2\right)^{3 / 2}} \hat{k}
$$
(예제3) Helmholtz coil
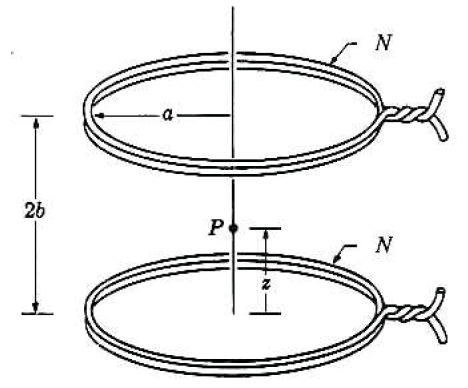
위 그림과 같이 반지름이 동일한 두 개의 전류고리가 나란하게 있으며,
두 코일 사이의 간격($2b$)이 각 전류고리의 반지름($a$)과 같을때 이 전류고리 쌍을 Helmholtz coil 이라고 한다.
Helmholtz coil은 축상에서 매우 균일한 자기장을 생성한다.
$$
B_z(z)=\frac{N \mu_0 I a^2}{2}\left\{\frac{1}{\left(z^2+a^2\right)^{3 / 2}}+\frac{1}{\left[(2 b-z)^2+a^2\right]^{3 / 2}}\right\}
$$
$$
\frac{d B_z}{d z}=\frac{\mu_0 N I a^2}{2}\left\{-\frac{3}{2} \frac{2 z}{\left(z^2+a^2\right)^{5 / 2}}-\frac{3}{2} \frac{2(z-2 b)}{\left[(2 b-z)^2+a^2\right]^{5 / 2}}\right\}
$$
$$
\begin{aligned}
\frac{d^2 B_z}{d z^2}= & -\frac{3 \mu_0 N I a^2}{2}\left\{\frac{1}{\left(z^2+a^2\right)^{5 / 2}}-\frac{5}{2} \frac{2 z^2}{\left(z^2+a^2\right)^{7 / 2}}\right. \\
& \left.+\frac{1}{\left[(2 b-z)^2+a^2\right]^{5 / 2}}-\frac{5}{2} \frac{2(z-2 b)^2}{\left[(2 b-z)^2+a^2\right]^{7 / 2}}\right\}
\end{aligned}
$$
$$
\left.\frac{d^2 B_z}{d z^2}\right|_{z=b}=-\frac{3 \mu_0 N I a^2}{2}\left\{\frac{b^2+a^2-5 b^2+b^2+a^2-5 b^2}{\left(b^2+a^2\right)^{7 / 2}}\right\}
$$
이것이 0이 되기 위해서는 다음이 만족해야한다.
$$
2 b = a
$$
위 조건하에서 Helmholtz coil의 중심에서의 자기장은 다음과 같이 얻어진다.
$$
B_z=\frac{\mu_0 N I}{a} \frac{8}{5^{3 / 2}} \quad \mathrm{T}
$$
$$B_z=\frac{32 \pi N}{5^{3 / 2} a} \frac{I}{10} \quad \mathrm{G} $$
$I$ : ampere $a$ : cm, $B$ : gauss
축상의 자기장이지만 중심에서 약간 벗어난 지점의 자기장은 다음과 같이 얻어진다.
$$
B_z(z)=B_z\left(\frac{1}{2} a\right)+\left.\left(z-\frac{1}{2} a\right) \frac{\partial B_z}{\partial z}\right|_{z=\frac{1}{2} a}+\cdots
$$
$$
B_z(z)=B_z\left(\frac{1}{2} a\right)+\left.\frac{1}{24}\left(z-\frac{1}{2} a\right)^4 \frac{\partial^4 B_z}{\partial z^4}\right|_{z=\frac{1}{2} a}+\cdots
$$
$$
B_z(z)=B_z(a / 2)\left\{1-\frac{144}{125}\left(\frac{z-a / 2}{a}\right)^4\right\} \text {. }
$$
(예제4) 솔레노이드(Solenoid)
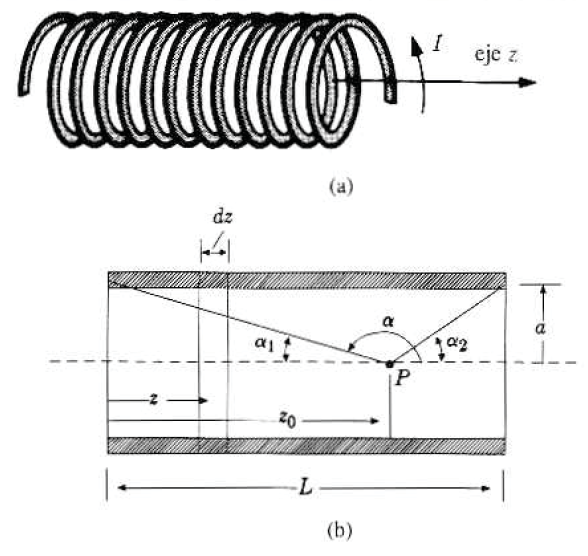
전류고리 하나가 만드는 축상에서의 자기장은 다음과 같이 주어진다.
$$
\vec{B}(z)=\frac{\mu_0 I}{2} \frac{a^2}{\left(z^2+a^2\right)^{3 / 2}} \hat{k}
$$
위 식을 활용하여 솔레노이드 내부의 자기장을 구한다. ($dI=(NI/L)dz$)
$$
B_z\left(z_0\right)=\frac{\mu_0 N I}{L} \frac{a^2}{2} \int_0^L \frac{d z}{\left[\left(z_0-z\right)^2+a^2\right]^{3 / 2}} .
$$
$z_0-z = a \cot \alpha$로 치환하면,
$$
\begin{aligned}
B_z(z_0) &=\frac{\mu_0 N I}{2 L} \int_{\alpha_2}^{\pi-\alpha_1} \sin \alpha d \alpha \\
&=\frac{\mu_0 N I}{2 L}\left[-\cos(\pi-\alpha_1)+\cos \alpha_2\right] \\
&=\frac{\mu_0 N I}{L}\left[\frac{\cos \alpha_1+\cos \alpha_2}{2}\right]
\end{aligned}
$$
만약 솔레노이드가 매우 길고 좁다면 다음과 같은 근사를 취하여 자기장을 구할 수 있다.
$$
\alpha_1 \cong \frac{a}{z_0} ; \quad \alpha_2 \cong \frac{a}{L-z_0} .
$$
$$
B_z\left(z_0\right) \cong \frac{\mu_0 N I}{L}\left\{1-\frac{a^2}{4 z_0^2}-\frac{a^2}{4\left(L-z_0\right)^2}\right\}
$$
7.5 Ampere의 법칙
전기장에대한 가우스법칙과 유사한 Ampere법칙이 있다.
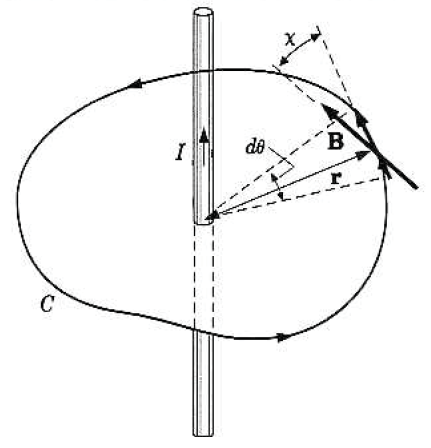
Ampere 법칙의 증명
정적 전류(stready current)에 대해서
$$
\nabla \cdot \vec{J}=0
$$
전류밀도 $\vec{J}$에 의한 자기장은 다음과 같이 주어진다.
$$
\vec{B}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} \int_V \frac{\vec{J}\left(\vec{r}_1\right) \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \quad 식(7-6)
$$
\begin{equation}
\nabla \times(\vec{F} \times \vec{G})=(\nabla \cdot \vec{G}) \vec{F}-(\nabla \cdot \vec{F}) \vec{G}+(\vec{G} \cdot \nabla) \vec{F}-(\vec{F} \cdot \nabla) \vec{G}
\end{equation}
위 관계를 이용하면 다음이 얻어진다.
\begin{aligned}
\nabla_2 \times \vec{B}\left(\vec{r}_2\right) &=\frac{\mu_0}{4 \pi} \int_v\left[\vec{J}\left(\vec{r}_1\right)\left(\nabla_2 \cdot \frac{\vec{r}_2-\vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|^3}\right) \right. \\
&\left. -\vec{J}\left(\vec{r}_1\right) \cdot \mathbf{\nabla}_2 \frac{\vec{r}_2-\vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|^3}\right] d v_1
\end{aligned}
\begin{aligned}
\nabla_2 \times \vec{B}\left(\vec{r}_2\right) &=\frac{\mu_0}{4 \pi} \int_V\left[\vec{J}\left(\vec{r}_1\right) 4 \pi \delta\left(\vec{r}_2-\vec{r}_1\right)\right. \\
&\left. -\vec{J}\left(\vec{r}_1\right) \cdot \nabla_1 \frac{\vec{r}_1-\vec{r}_2}{\left|\vec{r}_1-\vec{r}_2\right|^3}\right] d v_1
\end{aligned}
$$
\nabla_1 \cdot\left(\vec{J} \frac{x_1-x_2}{\left|\vec{r}_1-\vec{r}_2\right|^3}\right)=\frac{x_1-x_2}{\left|\vec{r}_1-\vec{r}_2\right|^3} \nabla_1 \cdot \vec{J}+\vec{J} \cdot \nabla_1 \frac{x_1-x_2}{\left|\vec{r}_1-\vec{r}_2\right|^3}
$$
$$
\nabla \times \vec{B}(\vec{r}_2) = \mu_0 \vec{J}\left(\vec{r}_2\right),
$$
위 식을 Ampere 법칙의 미분형이라고 한다.
$$
\int_S \nabla \times \vec{B} \cdot \hat{n} d a=\int_C \vec{B} \cdot d \vec{\ell} .
$$
$$
\oint_C \vec{B} \cdot d \vec{\ell}=\mu_0 \int_S \vec{J} \cdot \hat{n} d a =\mu_0 I
$$
위 식을 Ampere 법칙이라고 한다.
(예제1) 직선 도선 주위의 자기장
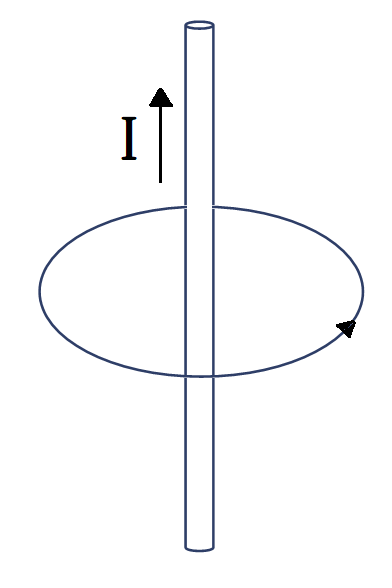
(예제2) 동축의 2개의 도선 전류
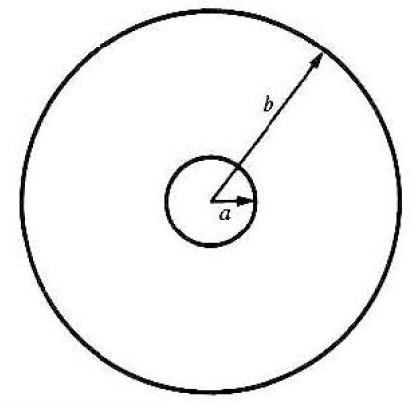
$$
\oint \vec{B} \cdot d l=2 \pi r B
$$
$$
\begin{array}{llrl}
2 \pi r B & =\mu_0 I, & & a < r < b \\
2 \pi r B & =0, & & b < r
\end{array}
$$
(예제3) 이상적인 solenoid 내의 자기장
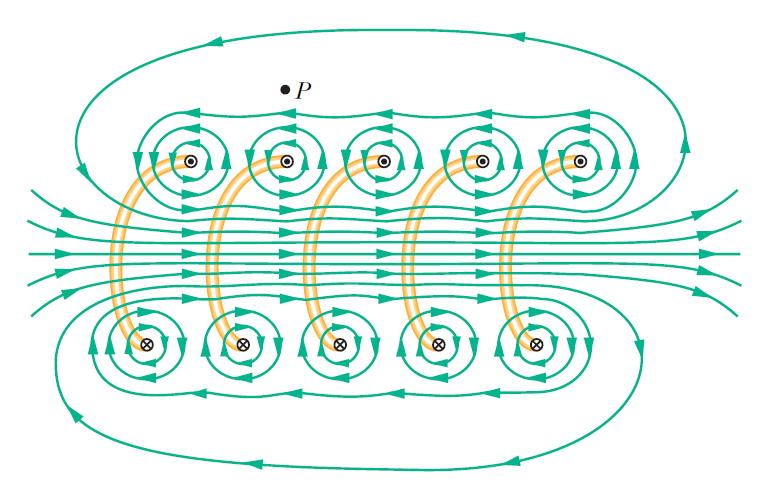
이상적인 solenoid는 무한한 길이를 가지고 있고, 고리 도선들을 충분히 촘촘하게 감아서
길이 방향으로 일정한 자기장을 가진다.
또한 solenoid 외부에는 자기장이 존재하지 않는다.
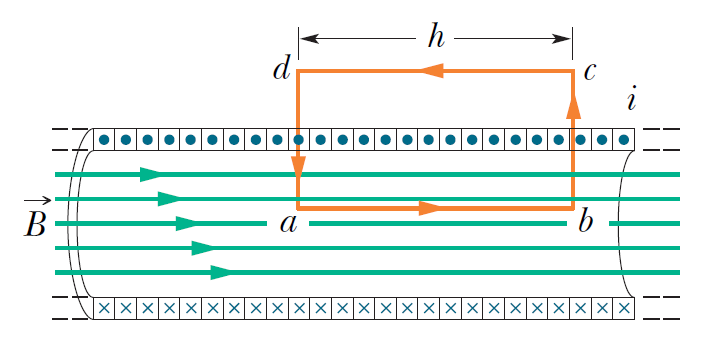
\begin{equation}
\oint \vec{B} \cdot d \vec{s}=\int_a^b \vec{B} \cdot d \vec{s}+\int_b^c \vec{B} \cdot d \vec{s}+\int_c^d \vec{B} \cdot d \vec{s}+\int_d^a \vec{B} \cdot d \vec{s}
\end{equation}
$$
B h=\mu_0 I N
$$
여기서 $N$은 길이 $h$에 감긴 횟수이다.
$$
B=\mu_0 I N/h = \mu_0 I n
$$
여기서 $n$은 단위길이당 감긴 횟수($N/h$)를 의미한다.
7.6 자기 벡터 potential
$$
\vec{B} = \nabla \times \vec{A}
$$
위와 같이 정의되는 벡터 $\vec{A}$를 자기 벡터 포텐셜(magnetic vector potential)이라고한다.
벡터 포텐셜은 다음과 같이 전류밀도로 표현될 수 있다.
$$
\vec{A}(\vec{r}_2)=\frac{\mu_0}{4 \pi} \int_V \frac{\vec{J}\left(\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1 .
$$
(증명1)
$$
\begin{aligned}
& \nabla \times \vec{B} = \nabla \times \nabla \times \vec{A}=\mu_0 \vec{J} \\
& \nabla \times \nabla \times \vec{A}=\nabla\nabla \cdot \vec{A}-\nabla^2 \vec{A}
\end{aligned}
$$
아래 식을 활용
\begin{equation}
\nabla \times(\nabla \times \vec{F})=\nabla(\nabla \cdot \vec{F})-\nabla^2 \vec{F}
\end{equation}
$$
\nabla^2 \vec{A}=-\mu_0 \vec{J}
$$
위 Poisson 방정식의 해는 다음과 같이 주어진다는 것을 정전기학에서 이미 배웠다.
$$
\vec{A}(\vec{r}_2)=\frac{\mu_0}{4 \pi} \int_V \frac{\vec{J}\left(\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1 .
$$
(증명2)
$$
\frac{\vec{r}_2-\vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|^3}=-\nabla_2 \frac{1}{\left|\vec{r}_2-\vec{r}_1\right|},
$$
$$
\nabla \times(\varphi \vec{F})=\varphi \nabla \times \vec{F}-\vec{F} \times \nabla \varphi,
$$
$$
\nabla_2 \times\left\{\frac{1}{\left|\vec{r}_2-\vec{r}_1\right|} \vec{J}\left(\vec{r}_1\right)\right\}=-\vec{J}\left(\vec{r}_1\right) \times \nabla_2 \frac{1}{\left|\vec{r}_2-\vec{r}_1\right|}
$$
$$
\begin{aligned}
\vec{B}\left(\vec{r}_2\right) & =\frac{\mu_0}{4 \pi} \int_V \vec{J}\left(\vec{r}_1\right) \times \frac{\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3} d v_1 \\
& =-\frac{\mu_0}{4 \pi} \int_V \vec{J}\left(\vec{r}_1\right) \times \nabla_2 \frac{1}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1 \\
& =\frac{\mu_0}{4 \pi} \int_V \nabla_2 \times \frac{\vec{J}\left(\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1 \\
& = \nabla_2 \times \left( \frac{\mu_0}{4 \pi} \int_V \frac{\vec{J}\left(\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1 \right)
\end{aligned}
$$
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} \int_{\boldsymbol{V}_1} \frac{\vec{J}\left(\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|} d v_1
$$
7.7 회로에서 매우 먼 영역에서의 자기장
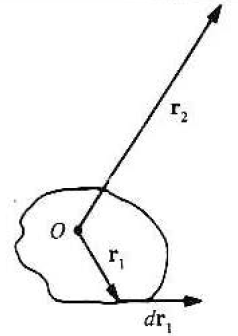
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0 I}{4 \pi} \oint \frac{d \vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|} .
$$
$$
\left|\vec{r}_2-\vec{r}_1\right|^{-1}=\left(r_2^2+r_1^2-2 \vec{r}_1 \cdot \vec{r}_2\right)^{-1 / 2}
$$
$$
\left|\vec{r}_2-\vec{r}_1\right|^{-1}=\frac{1}{r_2}\left[1+\frac{\vec{r}_1 \cdot \vec{r}_2}{r_2^2}+\cdots\right]
$$
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0 I}{4 \pi}\left\{\frac{1}{r_2} \oint d \vec{r}_1+\frac{1}{r_2^3} \oint d \vec{r}_1\left(\vec{r}_1 \cdot \vec{r}_2\right)+\cdots\right\} .
$$
$$
\left(\vec{r}_1 \times d \vec{r}_1\right) \times \vec{r}_2=-\vec{r}_1\left(\vec{r}_2 \cdot d \vec{r}_1\right)+d \vec{r}_1\left(\vec{r}_1 \cdot \vec{r}_2\right)
$$
$$
d\left[\vec{r}_1\left(\vec{r}_2 \cdot \vec{r}_1\right)\right]=\vec{r}_1\left(\vec{r}_2 \cdot d \vec{r}_1\right)+d \vec{r}_1\left(\vec{r}_2 \cdot \vec{r}_1\right),
$$
$$
d \vec{r}_1\left(\vec{r}_1 \cdot \vec{r}_2\right)=\frac{1}{2}\left(\vec{r}_1 \times d \vec{r}_1\right) \times \vec{r}_2+\frac{1}{2} d\left[\vec{r}_1\left(\vec{r}_2 \cdot \vec{r}_1\right)\right] .
$$
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi}\left[\frac{I}{2} \vec{r}_1 \times d \vec{r}_1\right] \times \frac{\vec{r}_2}{r_2^3} .
$$
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} \frac{\vec{m} \times \vec{r}_2}{r_2^3}
$$
$$
\begin{aligned}
\vec{B}\left(\vec{r}_2\right)=\nabla \times \vec{A}\left(\vec{r}_2\right) & =\frac{\mu_0}{4 \pi} \nabla \times\left(\vec{m} \times \frac{\vec{r}_2}{r_2^3}\right) \\
& =\frac{\mu_0}{4 \pi}\left[-(\vec{m} \cdot \nabla) \frac{\vec{r}_2}{r_2^3}+\vec{m} \nabla \cdot \frac{\vec{r}_2}{r_2^3}\right] .
\end{aligned}
$$
$$
\begin{gathered}
m_x \frac{\partial}{\partial x_2}\left(\frac{\vec{r}_2}{r_2^3}\right)=\frac{m_x \hat{i}}{r_2^3}-3 m_x x_2 \frac{\vec{r}_2}{r_2^5} ; \\
(\vec{m} \cdot \vec{v}) \frac{\vec{r}_2}{r_2^3}=\frac{\vec{m}}{r_2^3}-\frac{3\left(\vec{m} \cdot \vec{r}_2\right) \vec{r}_2}{r_2^5} .
\end{gathered}
$$
$$
\nabla \cdot \frac{\vec{r}_2}{r_2^3}=\frac{3}{r_2^3}-\vec{r}_2 \cdot \frac{3 \vec{r}_2}{r_2^5}=0 . \quad\left(r_2 \neq 0\right)
$$
\begin{equation}
\vec{B}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi}\left[-\frac{\vec{m}}{r_2^3}+\frac{3\left(\vec{m} \cdot \vec{r}_2\right) \vec{r}_2}{r_2^5}\right]
\end{equation}
7.8 자기 스칼라 potential
$$
\vec{B}=-\mu_0 \nabla \varphi^*
$$
위와 같이 정의되는 $\varphi^*$을 자기 스칼라 포텐셜(magnetic scalar potential)이라고 한다.
$\nabla \cdot \vec{B}=0$ 이 사실을 고려한다면,
자기 스칼라 포텐셜은 아래와 같이 Laplace방정식을 만족한다는 것을 알 수 있다.
$$
\nabla \cdot \vec{B}=-\mu_0 \nabla^2 \varphi^*=0
$$
그러나 주의할 것은 전기 포텐셜의 경우와 차이가 있으니 주의할 필요가 있다.
• 자기 쌍극자 모먼트에 의한 스칼라 포텐셜
$$
\begin{aligned}
\vec{B}\left(\vec{r}_2\right)&=-\mu_0 \nabla\left(\frac{\vec{m} \cdot \vec{r}_2}{4 \pi r_2^3}\right) \\
\varphi^*\left(\vec{r}_2\right)&=\frac{\vec{m} \cdot \vec{r}_2}{4 \pi r_2^3}
\end{aligned}
$$
자기 쌍극자 모먼트의 스칼라 포텐셜이 위와 같이 주어진다.
• 임의 회로에 의한 스칼라 포텐셜
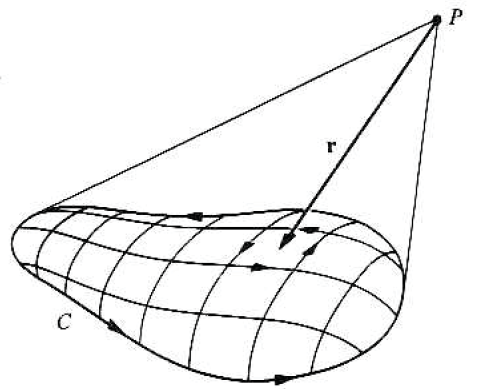
$$
d \vec{m}= I\hat{n} d a
$$
$$
\varphi^*(P)=\frac{I}{4 \pi} \int_s \frac{\vec{r}_2 \cdot \hat{n} d a}{r_2^3} .
$$
$$
\varphi^*(P)=-\frac{I}{4 \pi} \int_s \frac{\vec{r} \cdot \hat{n} d a}{r^3} .
$$
$$
\varphi^*(P)=-\frac{I \Omega}{4 \pi}
$$
7.9 자기 다발(자속, magnetic flux)
자기 다발(자속, magnetic flux)은 다음과 같이 정의된다.
$$
\Phi=\int_S \vec{B} \cdot \hat{n} d a
$$
자기 다발의 단위는 Wb(weber)이다.
자기 홀극은 존재하지 않으므로,
폐곡면에 대한 $\vec{B}$의 적분은 0이 된다.
$$
\oint_S \vec{B} \cdot \hat{n} d a=\int_V \nabla \cdot \vec{B} d v=0 .
$$