8. PN 다이오드
8.1 PN 접합 전류
8.1.1 PN 접합에서 전류의 정성적 기술
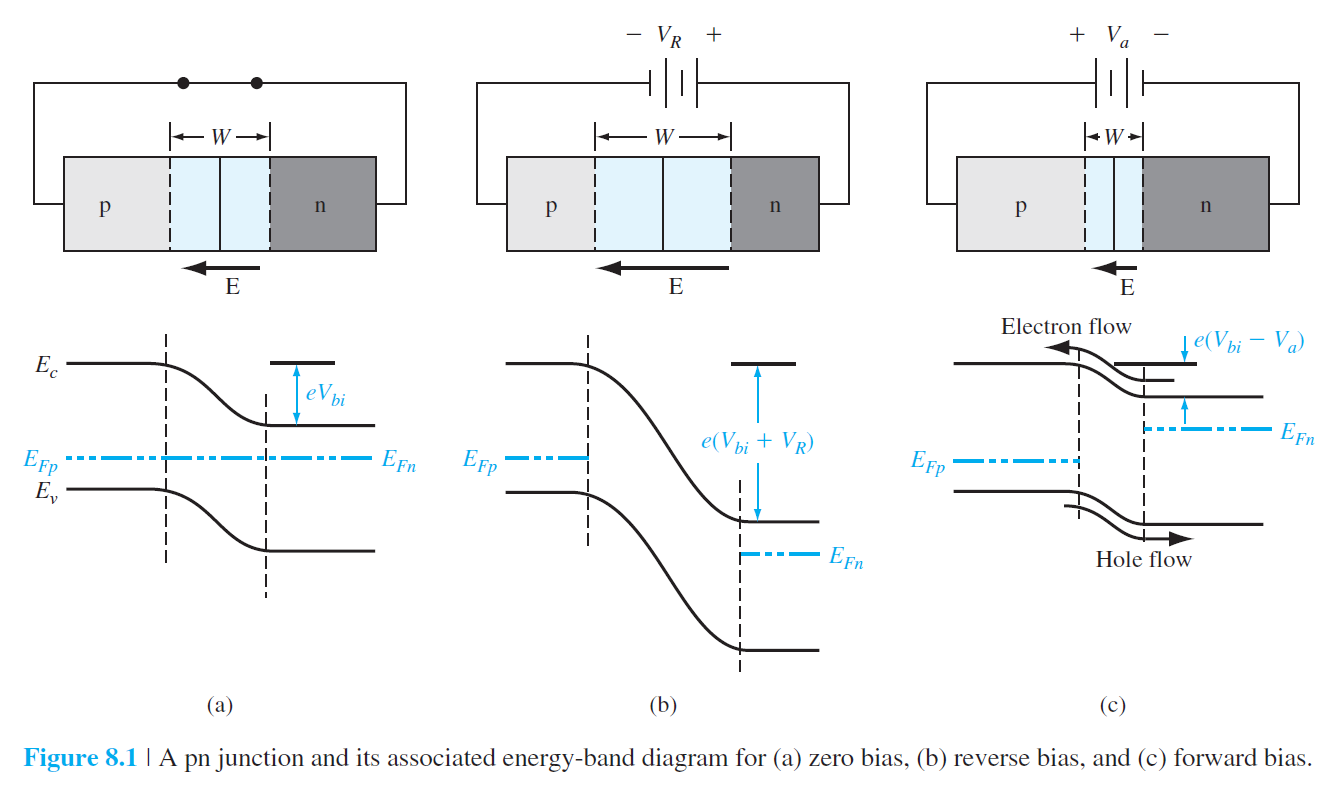 그림 8.1은 PN 접합에서의 영전압(a), 역전압(b), 순전압(b)이 가해질 경우의 전류의 발생원리를 설명한다.
그림 8.1은 PN 접합에서의 영전압(a), 역전압(b), 순전압(b)이 가해질 경우의 전류의 발생원리를 설명한다.
8.1.2 이상적인 전류-전압 관계
2. Maxwell-Boltzmann 근사 적용
3. 저주입 및 완전이온화 적용
4a. 총 전류는 전체 pn 구조에서 일정
4b. 전자와 홀 전류는 pn 구조를 통해 연속 함수
4c. 전자와 홀 전류는 공핍 영역 전체에서 일정

8.1.3 경계조건
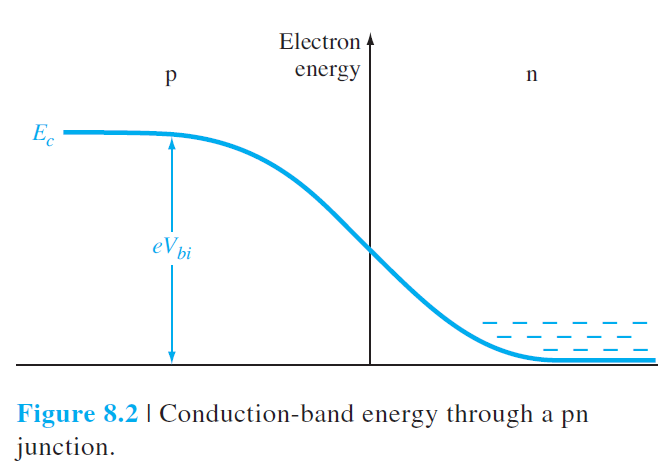
그림 8.2는 N영역의 conduction 밴드에 전자가 많이 있지만, built-in 포텐셜 장벽으로 인하여 전자들이 N영역에 갇혀있는 것을 보여준다. 번저 평형 상태에서 공핍층 양 끝단의 운반자 농도를 구해보자. $$ V_{b i} = V_t \ln \left(\frac{N_a N_d}{n_i^2}\right) \qquad (7.10) $$ Built-in 포텐셜식 (7.10)식으로부터 다음을 얻는다. $$ \frac{n_i^2}{N_a N_d}=\exp \left(\frac{-e V_{b i}}{k T}\right) \qquad (8.1) $$ N영역에서 평형상태의 다수 운반자 농도(전자)는 다음과 같이 주어지고 $$ n_{n 0} \approx N_d \qquad (8.2) $$ P영역에서 평형상태의 소수 운반자 농도(전자)는 다음과 같이 주어진다. 아래 첨자에 있는 p와 n은 영역을 의미한다. 위 식들을 정리하면 다음을 얻는다. $$ n_{p 0} \approx \frac{n_i^2}{N_a} \qquad (8.3) $$ 이 식은 평형상태에서 P영역과 N영역에서의 전자의 농도 사이의 관계를 말해준다.
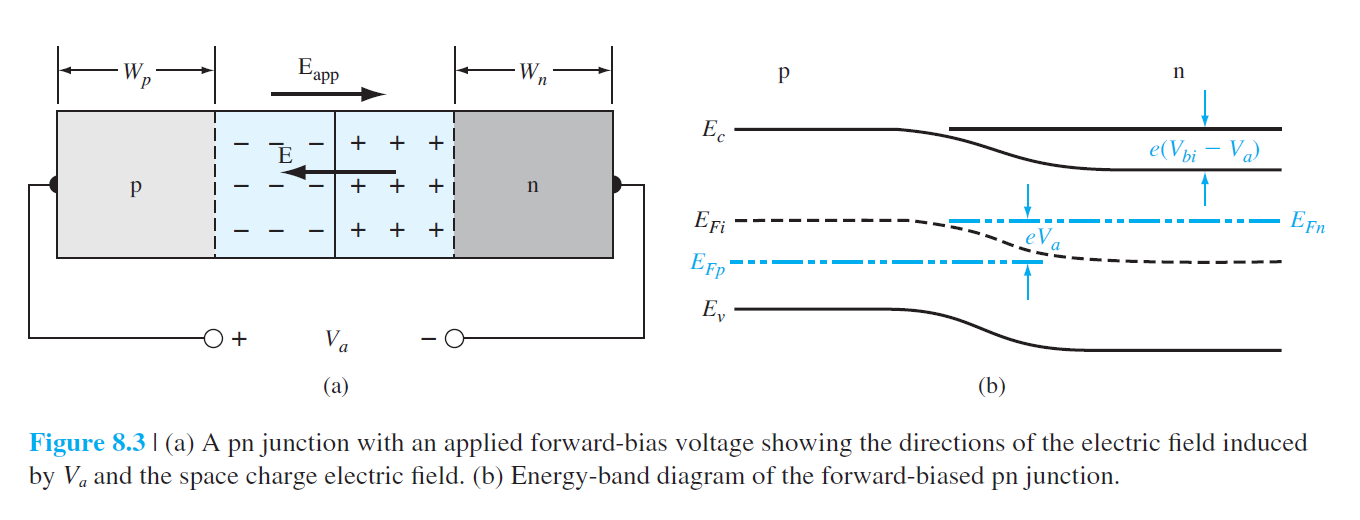
그림 8.3은 순전압인 경우에 전류 생성의 메커니즘을 보여준다. 평형상태에서는 확산과 유도전기장이 균형을 이루는데, 순전압에서는 유도전기장이 약화되어 확산이 활발히 일어나게 된다. 확산을 통해 P영역에서 N영역으로 홀이 이동하거나 N영역에서 P영역으로 전자가 이동하면, 다수 운반자에서 소수 운반자가 된다. 그래서 순전압에서 공핍층을 흐르는 전류는 소수 운반자에 의한 확산 전류인 것이다. 순전압 $V_a$을 가했을 때 공핍층 양끝단의 운반자 농도를 구해보자. $$ n_{p 0}=n_{n 0} \exp \left(\frac{-e V_{bi}}{k T}\right) \qquad (8.4) $$ 순전압 $V_a$을 가했을 때 P영역에서 전자의 농도는 (8.4)식에서 $V_{bi}$를 $V_{bi}-V_a$으로 대체하여 얻어진다. $$ n_p=n_{n 0} \exp \left(\frac{-e\left(V_{b i}-V_a\right)}{k T}\right)=n_{n 0} \exp \left(\frac{-e V_{b i}}{k T}\right) \exp \left(\frac{+e V_a}{k T}\right) $$ (8.5)
결과적으로 P와 N 각 영역에서 소수 운반자 농도는 다음과 같이 주어지며, 이것들은 공핍층 양끝단에서의 소수 운반자 농도이기도 하다. $$ n_p=n_{p 0} \exp \left(\frac{e V_a}{k T}\right) \qquad (8.6) $$ $$ p_n=p_{n 0} \exp \left(\frac{e V_a}{k T}\right) \qquad (8.7) $$
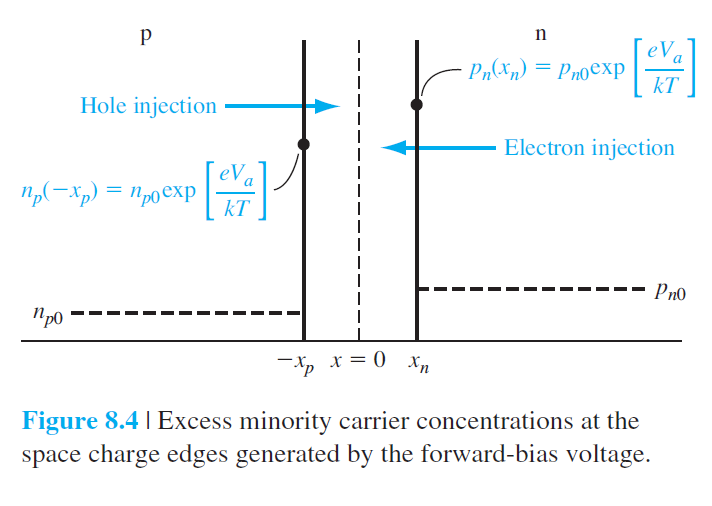
그림 8.4는 이렇게 결정된 공핍층 양끝단의 소수 운반자 농도를 표시하고 있다.

8.1.4 소수 운반자 분포
다음의 가정을 하자.
• 중성 영역에서 전기장이 0이다. → $E=0$
• 중성 영역에서 쌍생성이 일어나지 않는다. → $g'=0$
• 정상(steady) 상태이다. → $\frac{\partial\left(\delta p_n\right)}{\partial t} = 0$
위 가정하에 다음 식이 성립한다. $$ \frac{d^2\left(\delta p_n\right)}{d x^2}-\frac{\delta p_n}{L_p^2}=0 \quad\left(x>x_n\right) \qquad (8.9) $$ 여기서 $L_p^2 = D_p \tau_{p0}$이다. $$ \frac{d^2\left(\delta n_p\right)}{d x^2}-\frac{\delta n_p}{L_n^2}=0 \quad\left(x < -x_p\right) \qquad (8.10) $$ 여기서 $L_n^2 = D_n \tau_{n0}$이다. 위 (8.9)식과 (8.10)식을 푸는데 있어서 경계조건은 다음과 같다. $$ \begin{gathered} p_n\left(x_n\right)=p_{n 0} \exp \left(\frac{e V_a}{k T}\right) \qquad (8.11a) \\ n_p\left(-x_p\right)=n_{p 0} \exp \left(\frac{e V_a}{k T}\right) \qquad (8.11b) \\ p_n(x \rightarrow+\infty)=p_{n 0} \qquad (8.11c) \\ n_p(x \rightarrow-\infty)=n_{p 0} \qquad (8.11d) \end{gathered} $$ (8.9)식과 (8.10)식의 일반해는 다음과 같이 주어진다. $$ \delta p_n(x)=p_n(x)-p_{n 0}=A e^{x / L_p}+B e^{-x / L_p} \quad\left(x \geq x_n\right) \qquad (8.12) $$ $$ \delta n_p(x)=n_p(x)-n_{p 0}=C e^{x / L_n}+D e^{-x / L_n} \quad\left(x \leq-x_p\right) \qquad (8.13) $$ 위 식들에서 계수 $A, B, C, D$는 (8.11)식에서 주어지는 경계조건으로부터 얻어질 수 있다. 이렇게 결정된 소수 운반자 농도들은 다음과 같이 주어진다.
$ x \geq x_n $에서 $$ \delta p_n(x)=p_n(x)-p_{n 0}=p_{n 0}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \exp \left(\frac{x_n-x}{L_p}\right) $$ (8.14)
$ x \leq-x_p $에서 $$ \delta n_p(x)=n_p(x)-n_{p 0}=n_{p 0}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \exp \left(\frac{x_p+x}{L_n}\right) $$ (8.15)
이렇게 결정된 소수운반자 농도가 그림 8.5에 나타난다.
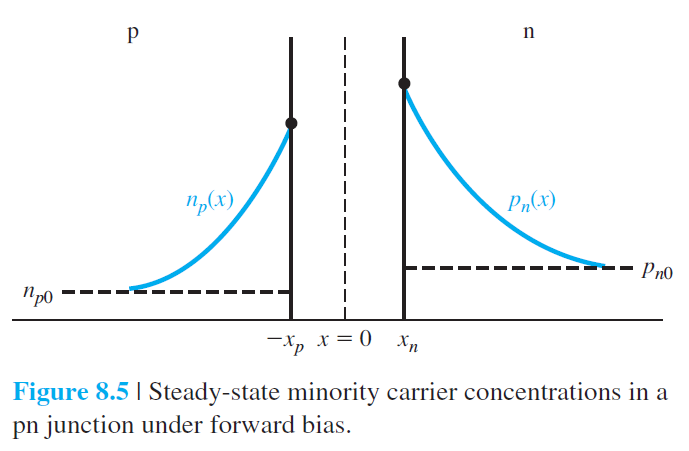
6장에서 비평형 상태의 운반자는 quasi-Fermi 준위와 다음과 같은 관계를 가지고 있음을 언급하였다. $$ p=p_0+\delta p=n_i \exp \left(\frac{E_{F i}-E_{F p}}{k T}\right) \qquad (8.16) $$ $$ n=n_0+\delta n=n_i \exp \left(\frac{E_{F n}-E_{F i}}{k T}\right) \qquad (8.17) $$
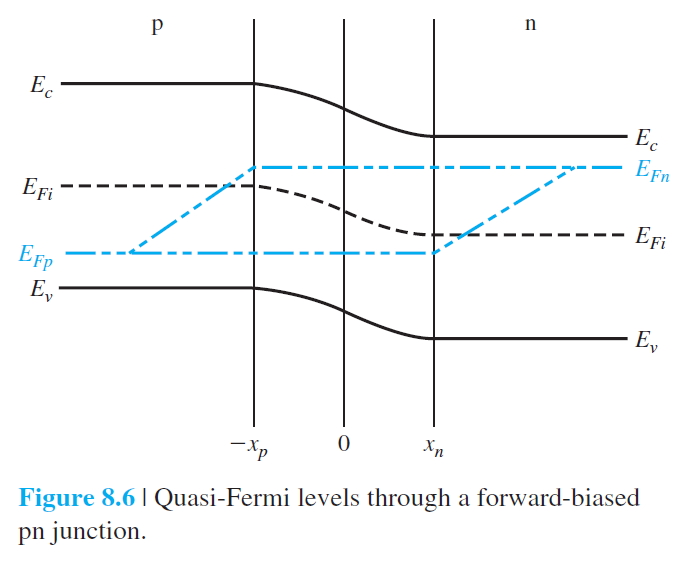
그림 8.6은 순전압에서 에너지 그래프를 보여주고 있다.
(8.14)와 (8.15)에서 과잉 운반자 밀도가 거리에 따라 exp함수로 주어지는 것을 보여준 만큼, 그림 8.6에서 quasi-Fermi 준위가 중성영역에서 거리에 따라 선형적으로 주어지는 것을 확인할 수 있다. $x=x_n$에서 $np$는 다음과 같이 쓸수있다. $$ n_0 p_n\left(x_n\right)=n_0 p_{n0} \exp \left(\frac{V_a}{V_t}\right)=n_i^2 \exp \left(\frac{V_a}{V_t}\right) \qquad (8.18) $$ (8.16)과 (8.17)을 조합하면 다음식을 얻는다. \begin{equation} n p=n_i^2 \exp \left(\frac{E_{F n}-E_{F p}}{k T}\right) \qquad (8.19) \end{equation} 위 식은 (8.18)식과 비교해 보면 quasi-Fermi 준위들의 차이 $E_{F n}-E_{F p}$가 $V_a$와 관련이 있음을 보여주고 또한 이 차이는 $np$로 얻을 수 있음을 의미한다. 공핍층에서는 이 차이가 일정하게 주어진다.
8.1.5 이상적인 PN 접합 전류
 전류는 5장에서 배운바와 같이 표류전류와 확산전류의 합으로 주어진다.
공핍층에서는 그림 8.5에서 보는 바와 같이 소수 운반자 농도의 기울기가 급격하게 나타나서 확산전류가 우세하게 나타나고,
공핍층의 양끝단에서는 전기장이 0이라고 가정하면 표류전류는 무시할 수 있다.
그래서 공핍층에서의 전류는 소수 운반자의 확산전류로 기술된다.
$x=x_n$에서의 소수운반자 홀의 확산전류밀도는 다음과 같이 주어진다.
$$
J_p\left(x_n\right)=-\left.e D_p \frac{d p_n(x)}{d x}\right|_{x=x_n} \qquad (8.20)
$$
균잏한 도핑을 가정하면 열평형 농도는 공간에 일정하므로 위 식은 아래와 같이 과잉전하로만 표시될 수 있다.
$$
J_p\left(x_n\right)=-\left.e D_p \frac{d\left(\delta p_n(x)\right)}{d x}\right|_{x=x_n} \qquad (8.21)
$$
(8.14)식을 미분하고 (8.21)식에 대입하면 다음 식이 얻어진다.
$$
J_p\left(x_n\right)=\frac{e D_p p_{n 0}}{L_p}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.22)
$$
이 전류는 순방향 전류이므로 $+x$ 방향이다.
유사하게 $x=-x_p$에서의 소수운반자 전자의 확산전류밀도는 다음과 같이 주어진다.
$$
J_n\left(-x_p\right)=\left.e D_n \frac{d\left(\delta n_p(x)\right)}{d x}\right|_{x=-x_p} \qquad (8.23)
$$
$$
J_n\left(-x_p\right)=\frac{e D_n n_{p 0}}{L_n}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.24)
$$
이 전류 또한 순방향 전류이므로 $+x$ 방향이다.
전체전류는 다음과 같이 전자와 홀 전류의 합으로 주어진다.
$$
J=J_p\left(x_n\right)+J_n\left(-x_p\right)=\left[\frac{e D_p p_{n 0}}{L_p}+\frac{e D_n n_{p 0}}{L_n}\right]\left[\exp \left(\frac{e V_a}{k T}\right)-1\right]
$$
(8.25)
\begin{equation}
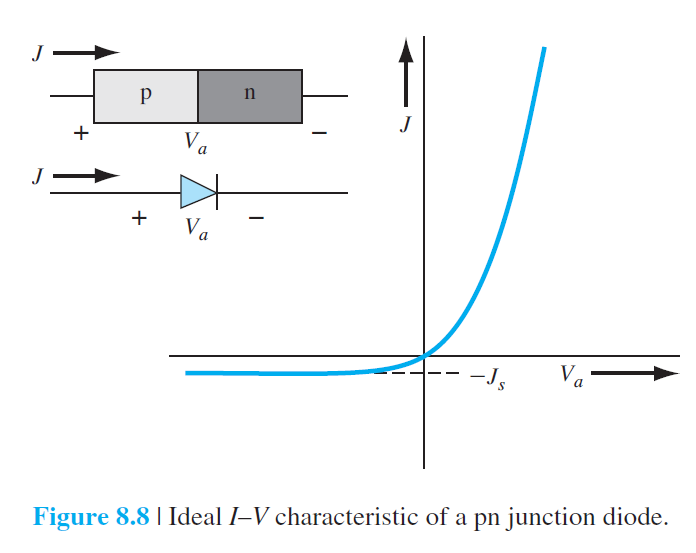
J=J_s\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.27)
\end{equation}
이 식을 이상적인 다이오드 방정식(ideal-diode equation)이라고 한다.
전류는 5장에서 배운바와 같이 표류전류와 확산전류의 합으로 주어진다.
공핍층에서는 그림 8.5에서 보는 바와 같이 소수 운반자 농도의 기울기가 급격하게 나타나서 확산전류가 우세하게 나타나고,
공핍층의 양끝단에서는 전기장이 0이라고 가정하면 표류전류는 무시할 수 있다.
그래서 공핍층에서의 전류는 소수 운반자의 확산전류로 기술된다.
$x=x_n$에서의 소수운반자 홀의 확산전류밀도는 다음과 같이 주어진다.
$$
J_p\left(x_n\right)=-\left.e D_p \frac{d p_n(x)}{d x}\right|_{x=x_n} \qquad (8.20)
$$
균잏한 도핑을 가정하면 열평형 농도는 공간에 일정하므로 위 식은 아래와 같이 과잉전하로만 표시될 수 있다.
$$
J_p\left(x_n\right)=-\left.e D_p \frac{d\left(\delta p_n(x)\right)}{d x}\right|_{x=x_n} \qquad (8.21)
$$
(8.14)식을 미분하고 (8.21)식에 대입하면 다음 식이 얻어진다.
$$
J_p\left(x_n\right)=\frac{e D_p p_{n 0}}{L_p}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.22)
$$
이 전류는 순방향 전류이므로 $+x$ 방향이다.
유사하게 $x=-x_p$에서의 소수운반자 전자의 확산전류밀도는 다음과 같이 주어진다.
$$
J_n\left(-x_p\right)=\left.e D_n \frac{d\left(\delta n_p(x)\right)}{d x}\right|_{x=-x_p} \qquad (8.23)
$$
$$
J_n\left(-x_p\right)=\frac{e D_n n_{p 0}}{L_n}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.24)
$$
이 전류 또한 순방향 전류이므로 $+x$ 방향이다.
전체전류는 다음과 같이 전자와 홀 전류의 합으로 주어진다.
$$
J=J_p\left(x_n\right)+J_n\left(-x_p\right)=\left[\frac{e D_p p_{n 0}}{L_p}+\frac{e D_n n_{p 0}}{L_n}\right]\left[\exp \left(\frac{e V_a}{k T}\right)-1\right]
$$
(8.25)
\begin{equation}
J=J_s\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.27)
\end{equation}
이 식을 이상적인 다이오드 방정식(ideal-diode equation)이라고 한다. $$ J_s=\frac{e D_p p_{n 0}}{L_p}+\frac{e D_n n_{p 0}}{L_n} \qquad (8.26) $$ $J_s$는 역포화 전류 밀도(reverse-saturation current density)라고 한다.
 |
 |


8.1.6 물리적 현상의 요약
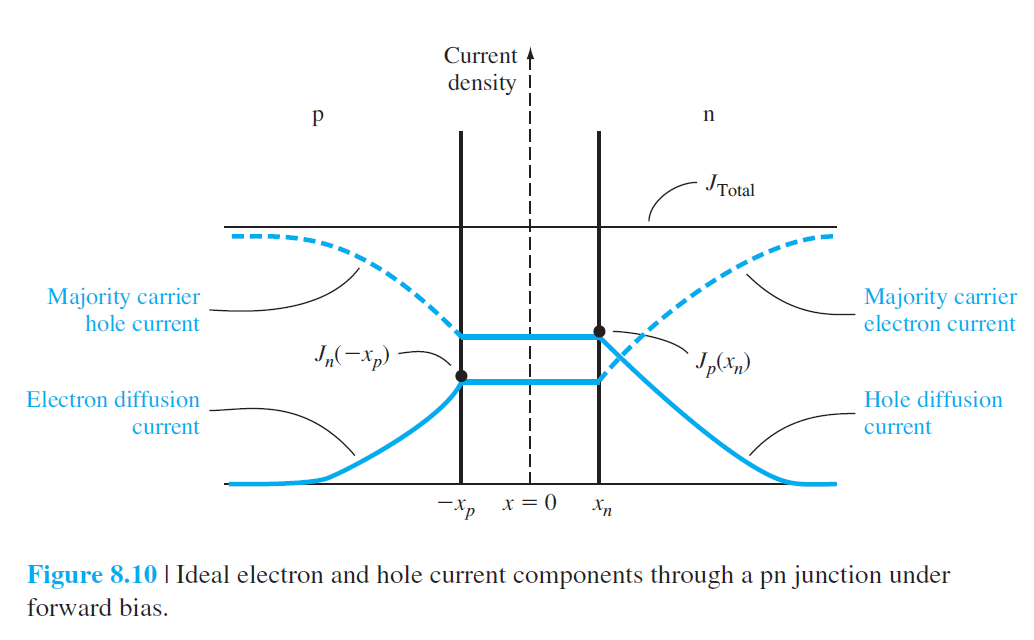
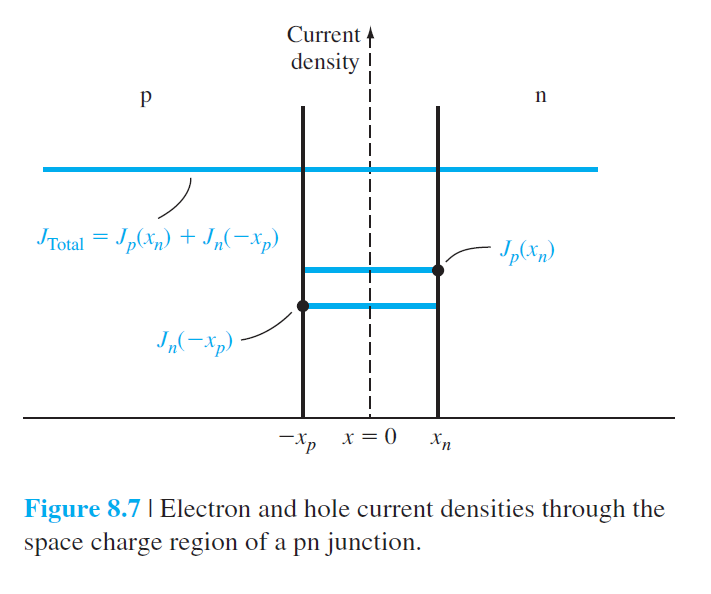
그림에서 전체 영역에서 총 전류밀도가 일정하다는 것이 나타나 있다. 실선은 소수 운반자에 의한 확산전류이고, 점선은 다수 운반자에 의한 표류전류이다.

8.1.7 온도 효과

8.1.8 짧은 다이오드
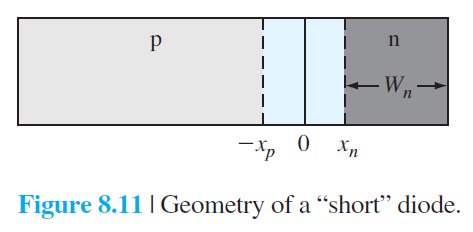
PN접합에서 어느 한쪽이 짧아서 그 영역이 확산 길이 $L$보다 짧은 경우를 생각해 보자. N영역이 $L_p$보다 짧은 경우가 그림 8.11에 보이고 있다. 이 경우 N영역내에 정상상태 과잉 소수 운반자 홀 농도는 (8.9)로 주어진다. $$ \frac{d^2\left(\delta p_n\right)}{d x^2}-\frac{\delta p_n}{L_p^2}=0 \qquad (8.9) $$ $x=x_n$에서 경계조건은 아래와 같이 주어진다. $$ p_n\left(x_n\right)=p_{n 0} \exp \left(\frac{e V_a}{k T}\right) \qquad (8.11a) $$ 다른 한쪽 끝 $x=x_n+W_n$에서 경계조건은 Ohmic 접촉으로 결정된다고 가정하자. 즉 과잉 소수 운반자 농도를 0으로 둔다. 그러면 다음의 경계조건이 결정된다. $$ p_n\left(x=x_n+W_n\right)=p_{n 0} \qquad (8.30) $$ (8.9)식의 일반해는 다음과 같이 (8.12)로 주어진다. $$ \delta p_n(x)=p_n(x)-p_{n 0}=A e^{x / L_p}+B e^{-x / L_p} \quad\left(x \geq x_n\right) $$ 경계조건을 적용하면, (8.9)식의 해는 다음과 같이 주어진다. $$ \delta p_n(x)=p_{n 0}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \frac{\sinh \left[\left(x_n+W_n-x\right) / L_p\right]}{\sinh \left[W_n / L_p\right]} \qquad (8.31) $$
(8.31)식의 유도 $$ \delta p_n=p_n-p_{n 0}=A e^{x / L_p}+B e^{-x / L_p} $$ $x=x_n$에서 경계조건 적용 $$ \begin{aligned} & \delta p_n=p_{n 0} \exp\left(\frac{e V_a}{k T}\right)-p_{n 0}=A e^{x_n / L_p}+B e^{-x_n / L_p} \\ & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right]=A e^{x_n / L_p}+B e^{-x_n / L_p} \\ \end{aligned} $$ $x = x_n + W$에서 경계조건 적용 $$ \begin{aligned} & \delta p_n=0=A e^{\left(x_n+W\right) / L_p}+B e^{-\left(x_n+W\right) / L_p} \\ & B=-A e^{2\left(x_n+W\right) / L_p} \\ \end{aligned} $$ 위 식들을 조합하여 $A$와 $B$를 구하면 다음과 같다. $$ \begin{aligned} & A = p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right] \frac{1}{e^{x_n / L_p}-e^{2\left(x_n+W\right) / L_p-x_n / L_p}} \\ & B= -p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right] \frac{e^{2\left(x_n+W\right) / L_p}}{e^{x_n / L_p}-e^{2\left(x_n+W\right) / L_p-x_n / L_p}} \\ \end{aligned} $$ $\delta p_n$는 다음과 같이 주어진다. $$ \begin{aligned} & \delta p_n=A e^{x / L_p}+B e^{-x / L_p} \\ = & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right] \frac{1}{e^{x_n / L_p}-e^{2\left(x_n+W\right) / L_p-x_n / L_p}} e^{x / L_p}- \\ & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right] \frac{e^{2\left(x_n+W\right) / L_p}}{e^{x_n / L_p}-e^{2\left(x_n+W\right) / L_p-x_n / L_p}} e^{-x / L_p} \\ = & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right]\left(\frac{e^{x / L_p}-e^{2\left(x_n+W\right) / L_p} e^{-x / L_p}}{e^{x_n / L_p}-e^{2\left(x_n+W\right) / L_p-x_n / L_p}}\right) \\ = & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right]\left(\frac{e^{\left(x_n+W-x\right) / L_p}-e^{-\left(x_n+W-x\right) / L_p}}{e^{W / L_p}-e^{-W / L_p}}\right) \\ = & p_{n 0}\left[\exp\left(\frac{e V_a}{k T}\right)-1\right] \frac{\sinh \left(\left(x_n+W-x\right) / L_p\right)}{\sinh \left(W / L_p\right)} \\ \end{aligned} $$
긴 다이오드 조건 $W_n\gg L_p$에서는 위 식이 (8.14)식과 같아진다. 만약 $W_n\ll L_p$ 로 가정하면 다음의 근사가 적용된다. $$ \begin{aligned} \sinh \left(\frac{x_n+W_n-x}{L_p}\right) & \approx\left(\frac{x_n+W_n-x}{L_p}\right) \qquad (8.32a)\\ \sinh \left(\frac{W_n}{L_p}\right) & \approx\left(\frac{W_n}{L_p}\right) \qquad (8.32b) \end{aligned} $$ 그러면 (8.31)은 다음과 같이 된다. $$ \delta p_n(x)=p_{n 0}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right]\left(\frac{x_n+W_n-x}{W_n}\right) \qquad (8.33) $$ 소수 운반자 농도가 거리의 선형함수가 된다.소수 운반자 홀의 확산 전류밀도는 다음과 같이 주어진다. $$ J_p=-e D_p \frac{d\left[\delta p_n(x)\right]}{d x} $$ $$ J_p(x)=\frac{e D_p p_{n 0}}{W_n}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (8.34) $$ 분모가 $L_p$가 아닌 $W_n$에 의존함을 알수있다. $W_n\ll L_p$이므로 짧은 다이오드의 확산 전류밀도가 긴 다이오드의 것보다 더 크다. 소수 운반자 농도가 거리의 선형함수이면, 짧은 영역 내에서 확산 전류밀도가 일정하다. 이것은 짧은 영역 내에서 재결합이 없다는 것을 의미한다
8.2 생성-재결합 전류와 고-수준 주입
8.2.1 생성-재결합 전류

• 역전압 생성전류
이미 아는 바와 같이 공핍층에서는 운반자가 거의 없다. ($n\approx p\approx 0$) 그러면 공핍층에서의 재결합율은 다음과 같이 주어진다.
$$ R=\frac{-C_n C_p N_t n_i^2}{C_n n'+C_p p'} \qquad (8.36) $$ 음의 부호는 전자-홀 쌍이 생성되고 있음을 의미한다. 공핍층에서 운반자가 없다는 것은 전자와 홀이 모두 결합되어 있다는 것을 의미하기때문에 더 이상 결합하기 보다는 쌍이 깨어질 일만 남았다는 것을 의미하기도 한다. 전자-홀 쌍은 트랩 준위를 통하여 생성되며, 전기장에 의해 역방향으로 추가적인 전류 흐름을 만들어 낸다. 이것을 역전압 생성전류(reverse-biased generation current)라고 한다. 이것은 그림 8.12에 잘 나타나있다.
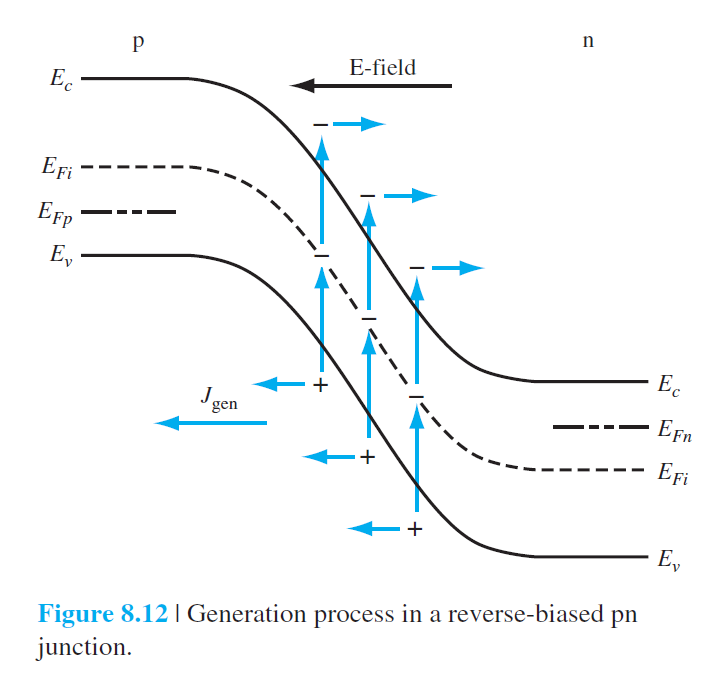
역전압 생성전류를 정량적으로 구해보자. 트랩의 준위가 intrinsic Fermi 준위와 같다면 $n'=p'=n_i$으로 주어진다. 그러면 (8.36)은 다음과 같이 주어진다. $$ R=\frac{-n_i}{\frac{1}{N_t C_p}+\frac{1}{N_t C_n}} \qquad (8.37) $$ (6.103)과 (6.104)의 수명의 정의를 사용하면 위 식은 다음과 같이 된다.
$$ R=\frac{-n_i}{\tau_{p 0}+\tau_{n 0}} \qquad (8.38) $$ 다음의 새로 정의된 평균 수명을 정의하면, $$ \tau_0=\frac{\tau_{p 0}+\tau_{n 0}}{2} \qquad (8.39) $$ 재결합율은 다음과 같이 된다. $$ R=-\frac{n_i}{2 \tau_0} \equiv -G \qquad (8.40) $$ 음의 재결합율은 생성율을 의미하며, $G$는 공핍층 내에서의 전자들과 홀들의 생성율이다. 생성 전류밀도는 연속방정식을 이용하면 다음과 같이 주어진다. $$ J_{\text {생성}}=\int_0^W e G d x = \frac{e n_i W}{2 \tau_0} \qquad (8.41) $$ 역전압에서 흐르는 총전류는 다음과 같이 주어진다. $$ J_R = J_s + J_{\text {생성}} \qquad (8.43) $$ $J_s$는 역전압에 무관한 값인데 비해, $J_{\text {생성}}$은 $W$에 의존하기 때문에, 역전압과 무관한 값이 아니다.
• 순전압 재결합 전류
순전압일 경우에는 중성영역에서 주입된 다수 운반자들이 공핍층으로 확산되면서 과잉 운반자를 형성하게 된다. 이 과잉 전자 운반자들과 과잉 홀 운반자들은 공핍층을 지나가면서 서로 재결합을 하게되어 소수 운반자 농도에 기여를 못하게 될수도 있다. 재결합 전류를 정량적으로 구해보자. SRH 이론에 의한 전자-홀 재결합율은 다음과 같이 구해진다. $$ R=\frac{C_n C_p N_t\left(n p-n_i^2\right)}{C_n\left(n+n'\right)+C_p\left(p+p'\right)} \qquad (8.35) $$ 분자 분모를 $C_n C_p N_t$로 나누고, 수명에 대한 정의를 이용하면, 위 식은 다음과 같이 된다. $$ R=\frac{n p-n_i^2}{\tau_{p 0}\left(n+n'\right)+\tau_{n 0}\left(p+p'\right)} \qquad (8.44) $$
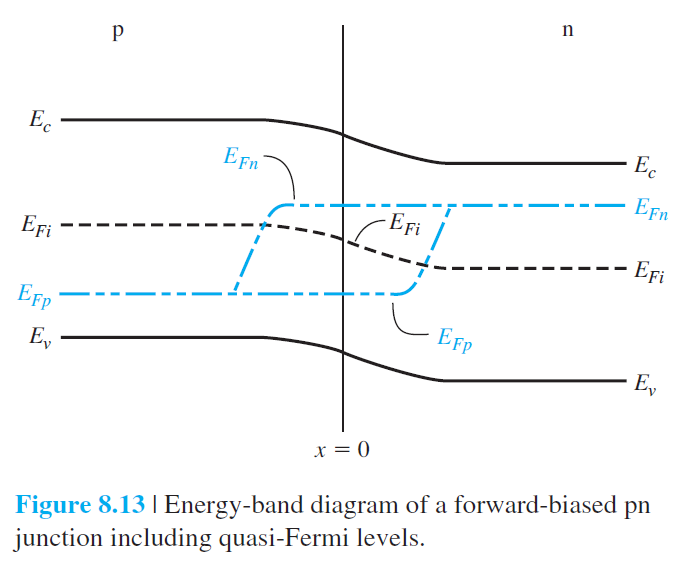
그림 8.13은 순전압에서 PN 접합의 에너지밴드 다이어그램을 보여준다.
6장에서 학습한 바와 같이 비평형 상태에서 전자와 홀의 농도는 다음과 같이 주어진다.
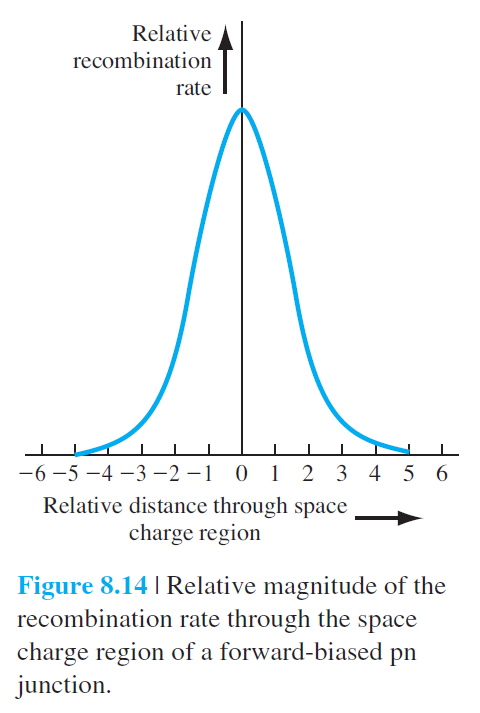
$$ n=n_i \exp \left[\frac{E_{F n}-E_{F i}}{k T}\right] \qquad (8.45) $$ $$ p=n_i \exp \left[\frac{E_{F i}-E_{F p}}{k T}\right] \qquad (8.46) $$ 그림 8.13에서 공핍층에서는 다음과 같이 주어짐을 알수있다. $$ \left(E_{F n}-E_{F i}\right)+\left(E_{F i}-E_{F p}\right)=e V_a \qquad (8.47) $$ 공핍층 정중앙에서는 다음과 같이 주어진다. $$ E_{F n}-E_{F i}=E_{F i}-E_{F p}=\frac{e V_a}{2} \qquad (8.48) $$ 그러면 공핍층 정중앙에서의 전자와 홀의 농도는 다음과 같이 주어진다. $$ \begin{aligned} n=n_i \exp \left(\frac{e V_a}{2 k T}\right) \qquad (8.49)\\ p=n_i \exp \left(\frac{e V_a}{2 k T}\right) \qquad (8.50) \end{aligned} $$ $n'=p'=n_i$와 $\tau_{n0}=\tau_{p0}=\tau$를 가정하면, 공핍층 정중앙에서의 재결합율은 다음과 같이 주어진다. $$ R_{\max }=\frac{n_i}{2 \tau_0} \frac{\left[\exp \left(e V_a / k T\right)-1\right]}{\left[\exp \left(e V_a / 2 k T\right)+1\right]}\qquad (8.51) $$ $V_a\gg kT/e$로 가정하면 위식은 다음과 같이 된다. $$ R_{\max }=\frac{n_i}{2 \tau_0} \exp \left(\frac{e V_a}{2 k T}\right) \qquad (8.52) $$ 재결합 전류밀도는 다음과 같이 주어진다. $$ J_{\text{재결합}}=\int_0^W e R d x \qquad (8.53) $$ 적분 결과는 다음과 같다. $$ J_{\text{재결합}}=e x' \frac{n_i}{2 \tau_0} \exp \left(\frac{e V_a}{2 k T}\right) \qquad (8.54) $$ $x'$는 최대 재결합율이 효과적으로 일어나는 길이이다. $\tau_0$를 적절히 재조정하여 위 식을 관습적으로 다음과 같이 쓴다. $$ J_{\text{재결합}}=\frac{e W n_i}{2 \tau_0} \exp \left(\frac{e V_a}{2 k T}\right)=J_{r 0} \exp \left(\frac{e V_a}{2 k T}\right) \qquad (8.55) $$ 여기서 $W$는 공핍층의 폭이다.
• 총순전압 전류
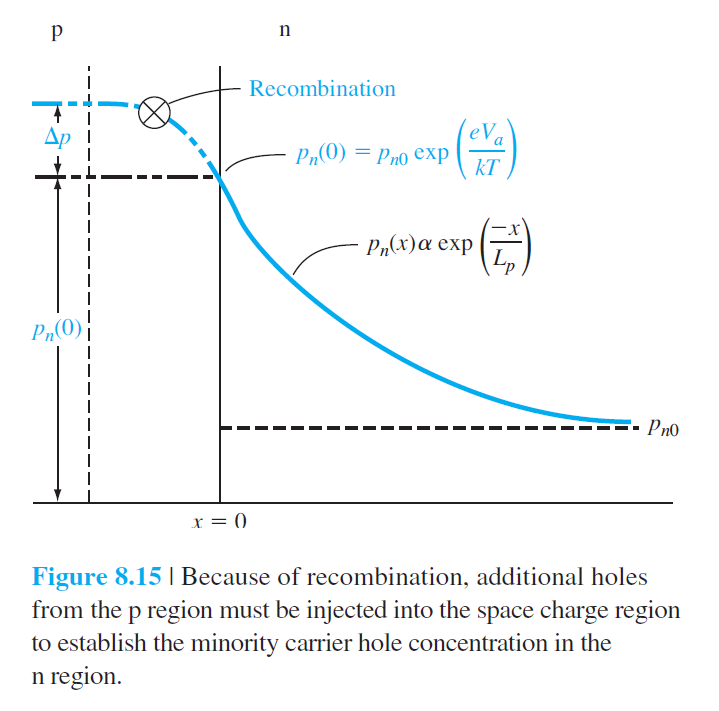
총순전압 전류밀도는 이상적인 전류밀도와 재결합 전류밀도의 합이다. 그림 8.15에서는 N 측 중성영역에서 소수 운반자의 공간분포를 보여주는 데 이 그래프는 그림 8.5와 동일하다. 만약 P영역에서 넘어오는 과잉 홀이 공핍층에서 재결합을 통해 사라진다면 이 사라지는 부분을 채우기 위해 P영역에서 추가적으로 홀이 공급되어야 한다. 이러한 과잉 운반자의 흐름이 재결합 전류로 나타난다.
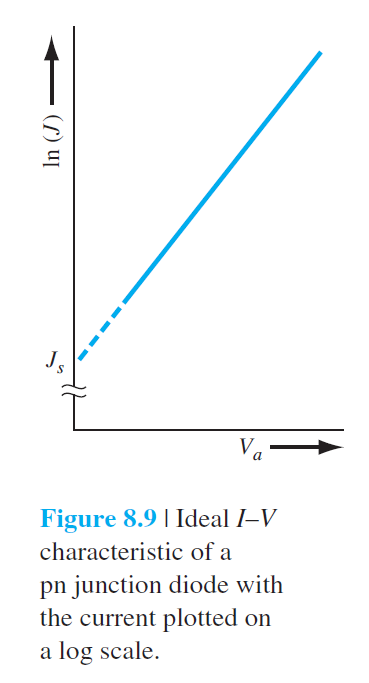
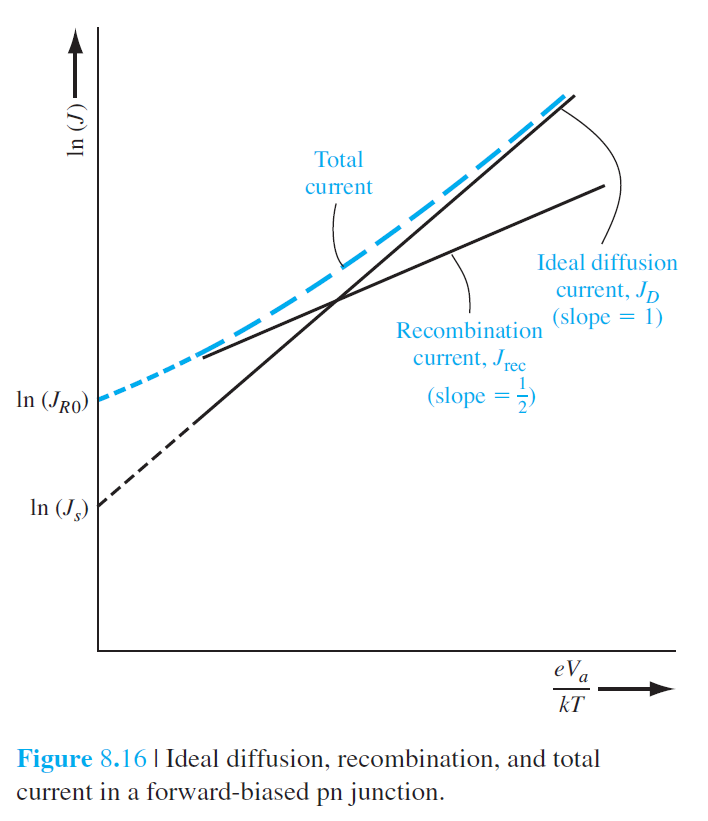
총순전압 전류밀도는 다음과 같이 주어진다. $$ J=J_{\text{재결합}} + J_D \qquad (8.56) $$ $$ J_D=J_s \exp \left(\frac{e V_a}{k T}\right) \qquad (8.57) $$ 식(8.56)은 다음과 같이 된다. $$ J=J_{r 0} \exp \left(\frac{e V_a}{2 k T}\right) + J_s \exp \left(\frac{e V_a}{k T}\right) \qquad (8.56) $$ (8.55)식과 (8.57)식의 양변을 로그 취하면 다음을 얻는다. $$ \begin{aligned} \ln J_{\text{재결합}} & = \ln J_{r 0}+\frac{e V_a}{2 k T } = \ln J_{r 0}+\frac{V_a}{2 V_t} \qquad (8.58a)\\ \ln J_D & = \ln J_s+\frac{e V_a}{k T} = \ln J_s+\frac{V_a}{V_t} \qquad (8.58b) \end{aligned} $$ 일반적으로 다이오드 전류-전압 관계는 다음과 같이 쓸수있다. $$ I=I_s\left[\exp \left(\frac{e V_a}{n k T}\right)-1\right] \qquad (8.59) $$ 여기서 $n$은 이상 인자(ideality factor)라고 부른다. 큰 순전압에서 확산이 우세할 때 $n\approx 1$이 되고, 작은 순전압에서 재결합이 우세할 때 $n\approx 2$이 된다. $1 < n < 2$인 전이 영역이 존재한다.
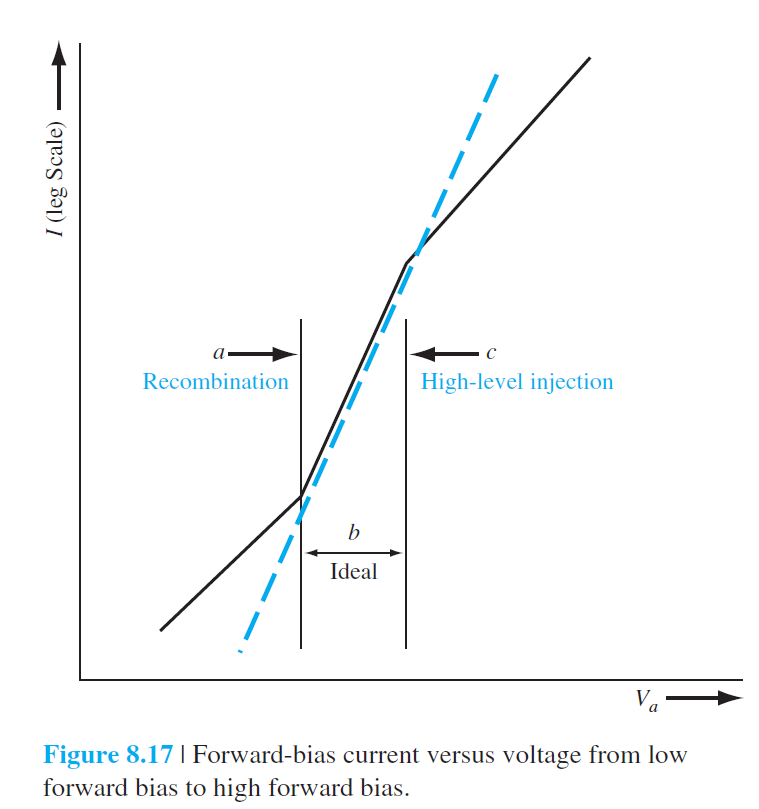
8.2.2 고-수준 주입
8.3 PN 접합의 소신호 모델
8.3.1 확산 저항(diffusion resistance)
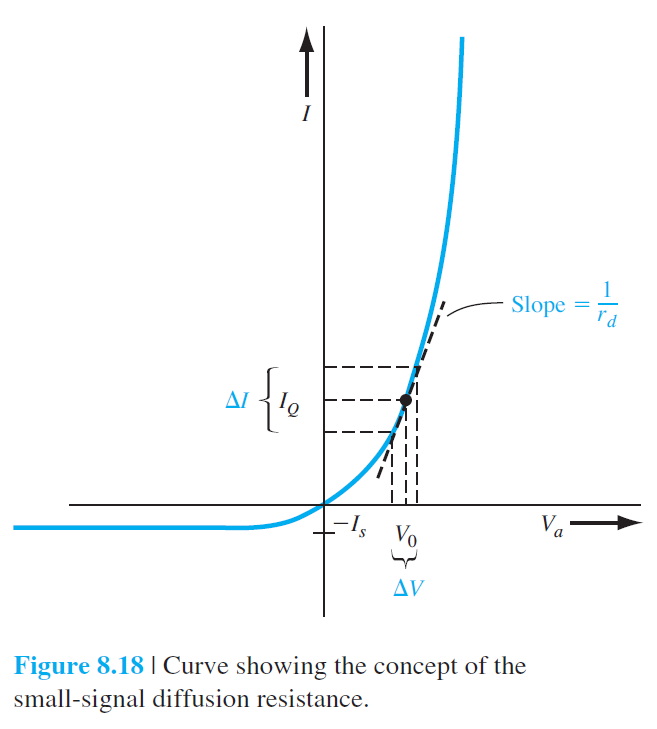
그림 8.18은 순전압 $V_0$ 근처에서 변화되는 전압에 대한 전류 값의 변화를 보여준다. 그림 8.18으로부터 증분 전도도(incremental conductance) $g_d$는 다음과 같이 정의된다. $$ g_d=\left.\frac{d I_D}{d V_a}\right|_{V_a=V_0} \qquad (8.65) $$ 증분 저항($r_d$)은 증분 전도도의 역수이며 다음과 같이 주어진다. $$ r_d=\left.\frac{d V_a}{d I_D}\right|_{I_D=I_{D Q}} \qquad (8.66) $$ $I_{D Q}$는 정지 다이오드 전류이다. 만약 다이오드가 충분히 강한 순전압하에 있다면, 증분 컨덕턴스는 다음과 같이 된다. $$ g_d=\left.\frac{d I_D}{d V_a}\right|_{V_a=V_0}=\left(\frac{e}{k T}\right) I_s \exp \left(\frac{e V_0}{k T}\right) \approx \frac{I_{D Q}}{V_t} \qquad (8.67) $$ 증분 저항은 다음과 같다. $$ r_d=\frac{V_t}{I_{D Q}} \qquad (8.68) $$ 증분 저항은 확산 저항(diffusion resistance)이라고도 한다.
8.3.2 소신호 admittance
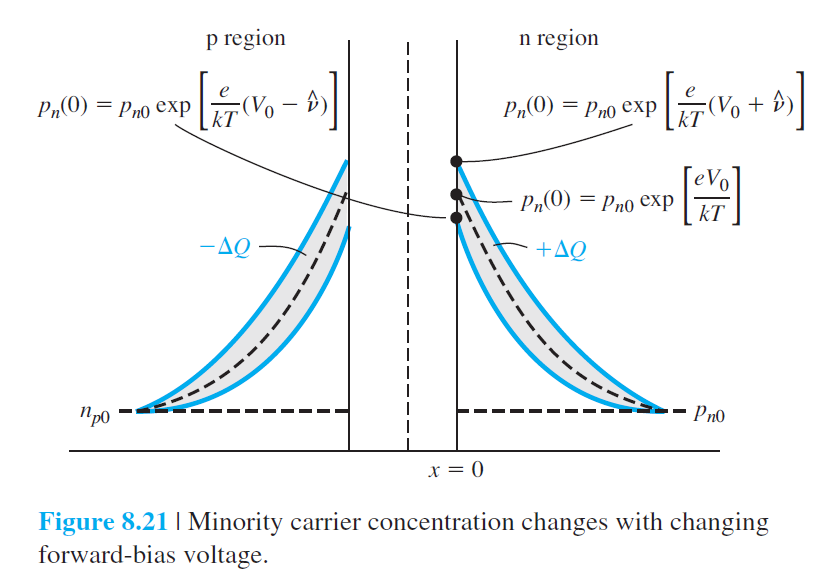
확산 전기용량(diffusion capacitance)
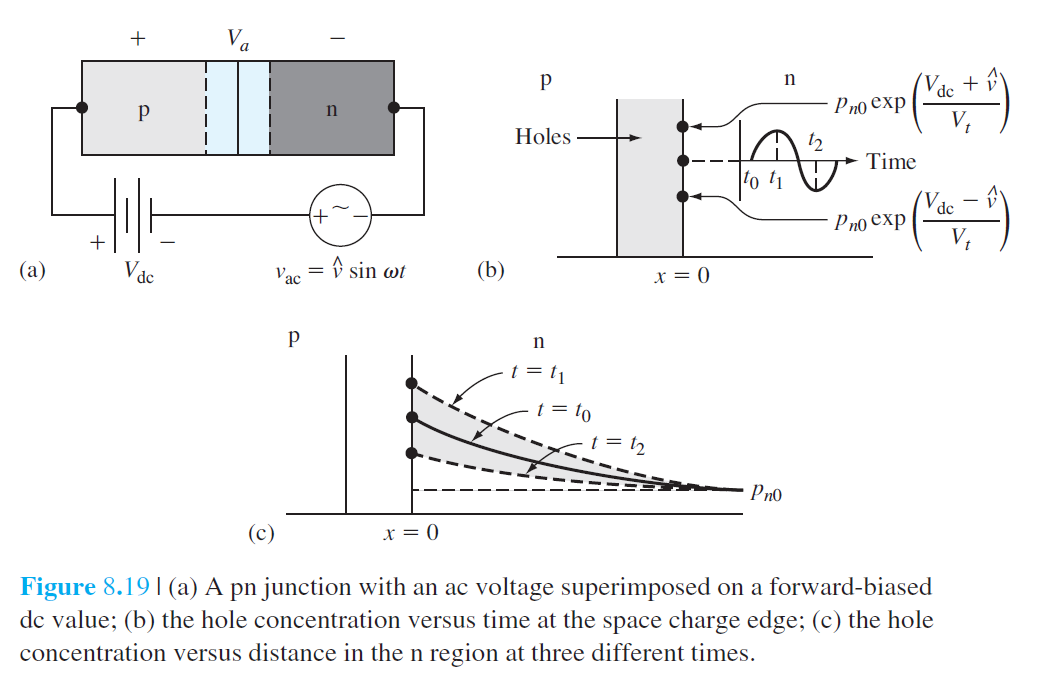
\begin{equation} V_a=V_0+v_1(t) \qquad (8.69) \end{equation} $$ p_n(x=0)=p_{n 0} \exp \left\{\frac{e\left[V_0+v_1(t)\right]}{k T}\right\}=p_n(0, t) \qquad (8.70) $$ $$ \begin{gathered} p_n(0, t)=p_{\mathrm{dc}} \exp \left[\frac{e v_1(t)}{k T}\right] \qquad (8.71)\\ p_{\mathrm{dc}}=p_{n 0} \exp \left(\frac{e V_0}{k T}\right) \qquad (8.72) \end{gathered} $$ $$ p_n(0, t) \approx p_{\mathrm{dc}}\left[1+\frac{v_1(t)}{V_t}\right] \qquad (8.73) $$ $$ p_n(0, t)=p_{\mathrm{dc}}\left(1+\frac{\hat{V}_1}{V_t} e^{j \omega t}\right) \qquad (8.74) $$ $$ D_p \frac{\partial^2\left(\delta p_n\right)}{\partial x^2}-\frac{\delta p_n}{\tau_{p 0}}=\frac{\partial\left(\delta p_n\right)}{\partial t} \qquad (8.75) $$ $$ \delta p_n(x, t)=\delta p_0(x)+p_1(x) e^{j \omega t} \qquad (8.76) $$ $$ D_p\left\{\frac{\partial^2\left[\delta p_0(x)\right]}{\partial x^2}+\frac{\partial^2 p_1(x)}{\partial x^2} e^{j \omega t}\right\}-\frac{\delta p_0(x)+p_1(x) e^{j \omega t}}{\tau_{p 0}}=j \omega p_1(x) e^{j \omega t} $$ (8.77) $$ \begin{aligned} &\left\{\frac{D_p \partial^2\left[\delta p_0(x)\right]}{\partial x^2}-\frac{\delta p_0(x)}{\tau_{p 0}}\right\}+\left[D_p \frac{\partial^2 p_1(x)}{\partial x^2}-\frac{p_1(x)}{\tau_{p 0}}-j \omega p_1(x)\right] e^{j \omega t} \\ & = 0 \qquad (8.78) \end{aligned} $$ $$ D_p \frac{d^2 p_1(x)}{d x^2}-\frac{p_1(x)}{\tau_{p 0}}-j \omega p_1(x)=0 \qquad (8.79) $$ $$ \begin{gathered} \frac{d^2 p_1(x)}{d x^2}-\frac{\left(1+j \omega \tau_{p 0}\right)}{L_p^2} p_1(x)=0 \qquad (8.80) \\ \frac{d^2 p_1(x)}{d x^2}-C_p^2 p_1(x)=0 \qquad (8.81)\\ C_p^2=\frac{\left(1+j \omega \tau_{p 0}\right)}{L_p^2} \qquad (8.82) \end{gathered} $$ $$ p_1(x)=K_1 e^{-C_p x}+K_2 e^{+C_p x} \qquad (8.83) $$ $$ p_1(x)=K_1 e^{-C_p x} \qquad (8.84) $$ $$ p_1(0)=K_1=p_{\mathrm{dc}}\left(\frac{\hat{V}_1}{V_t}\right) \qquad (8.85) $$ $$ J_p=-\left.e D_p \frac{\partial p_n}{\partial x}\right|_{x=0} \qquad (8.86) $$ $$ J_p=-\left.e D_p \frac{\partial\left(\delta p_n\right)}{\partial x}\right|_{x=0}=-\left.e D_p \frac{\partial\left[\delta p_0(x)\right]}{\partial x}\right|_{x=0}-\left.e D_p \frac{\partial p_1(x)}{\partial x}\right|_{x=0} e^{j \omega t} $$ (8.87) $$ \begin{gathered} J_p=J_{p 0}+j_p(t) \qquad (8.88)\\ J_{p 0}=-\left.e D_p \frac{\partial\left[\delta p_0(x)\right]}{\partial x}\right|_{x=0}=\frac{e D_p p_{n 0}}{L_p}\left[\exp \left(\frac{e V_0}{k T}\right)-1\right] \qquad (8.89) \end{gathered} $$ $$ j_p(t)=\hat{J}_p e^{j \omega t}=-\left.e D_p \frac{\partial p_1(x)}{\partial x} e^{j \omega t}\right|_{x=0} \qquad (8.90) $$ $$ \hat{J}_p=-\left.e D_p\left(-C_p\right)\left[p_{\mathrm{dc}}\left(\frac{\hat{V}_1}{V_t}\right)\right] e^{-c_p x}\right|_{x=0} \qquad (8.91) $$ $$ \hat{I}_p=A \hat{J}_p=e A D_p C_p p_{\mathrm{dc}}\left(\frac{\hat{V}_1}{V_t}\right) \qquad (8.92) $$ $$ \hat{I}_p=\frac{e A D_p p_{\mathrm{dc}}}{L_p} \sqrt{1+j \omega \tau_{p 0}}\left(\frac{\hat{V}_1}{V_t}\right) \qquad (8.93) $$ $$ I_{p 0}=\frac{e A D_p p_{d c}}{L_p}=\frac{e A D_p p_{n 0}}{L_p} \exp \left(\frac{e V_0}{k T}\right) \qquad (8.94) $$ $$ \hat{I}_p=I_{p 0} \sqrt{1+j \omega \tau_{p 0}}\left(\frac{\hat{V}_1}{V_t}\right) \qquad (8.95) $$ $$ \hat{I}_n=I_{n 0} \sqrt{1+j \omega \tau_{n 0}}\left(\frac{\hat{V}_1}{V_t}\right) \qquad (8.96) $$ $$ I_{n 0}=\frac{e A D_n n_{p 0}}{L_n} \exp \left(\frac{e V_0}{k T}\right) \qquad (8.97) $$ $$ Y=\frac{\hat{I}}{\hat{V}_1}=\frac{\hat{I}_p+\hat{I}_n}{\hat{V}_1}=\left(\frac{1}{V_t}\right)\left[I_{p 0} \sqrt{1+j \omega \tau_{p 0}}+I_{n 0} \sqrt{1+j \omega \tau_{n 0}}\right] $$ (8.98) $$ \begin{aligned} & \omega \tau_{p 0} \ll 1 \qquad (8.99a)\\ & \omega \tau_{n 0} \ll 1 \qquad (8.99b) \end{aligned} $$ $$ \begin{aligned} & \sqrt{1+j \omega \tau_{p 0}} \approx 1+\frac{j \omega \tau_{p 0}}{2} \qquad (8.100a)\\ & \sqrt{1+j \omega \tau_{n 0}} \approx 1+\frac{j \omega \tau_{n 0}}{2} \qquad (8.100b) \end{aligned} $$ $$ Y=\left(\frac{1}{V_t}\right)\left[I_{p 0}\left(1+\frac{j \omega \tau_{p 0}}{2}\right)+I_{n 0}\left(1+\frac{j \omega \tau_{n 0}}{2}\right)\right] \qquad (8.101) $$ $$ Y=\left(\frac{1}{V_t}\right)\left(I_{p 0}+I_{n 0}\right)+j \omega\left[\left(\frac{1}{2 V_t}\right)\left(I_{p 0} \tau_{p 0}+I_{n 0} \tau_{n 0}\right)\right]\qquad (8.102) $$ PN 접합 어드미턴스는 다음과 같이 주어진다. $$ Y=g_d+j \omega C_d \qquad (8.103) $$ $g_d$는 다음과 같이 주어지는 확산 전도도(diffusion conductance)이다. $$ g_d=\left(\frac{1}{V_t}\right)\left(I_{p 0}+I_{n 0}\right)=\frac{I_{D Q}}{V_t} \qquad (8.104) $$ $C_d$는 다음과 같이 주어지는 확산 전기용량(diffusion capacitance)이다. $$ C_d=\left(\frac{1}{2 V_t}\right)\left(I_{p 0} \tau_{p 0}+I_{n 0} \tau_{n 0}\right) \qquad (8.105) $$

8.3.3 등가회로
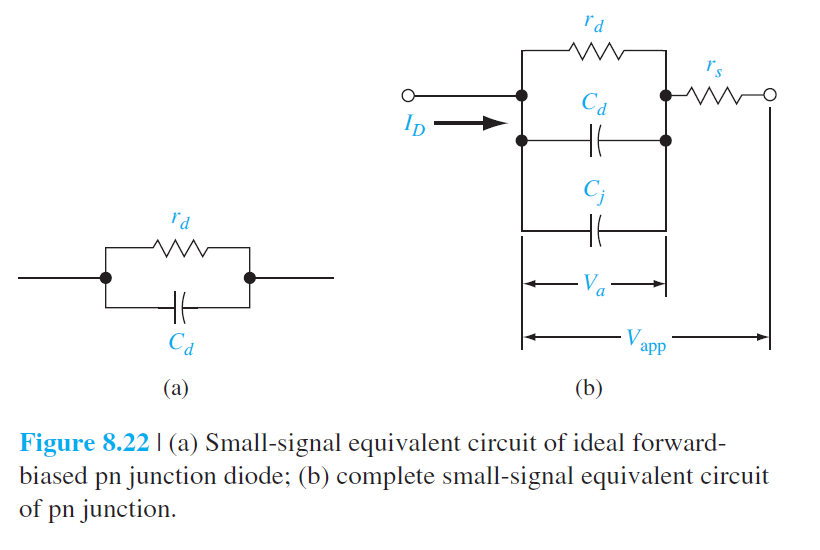
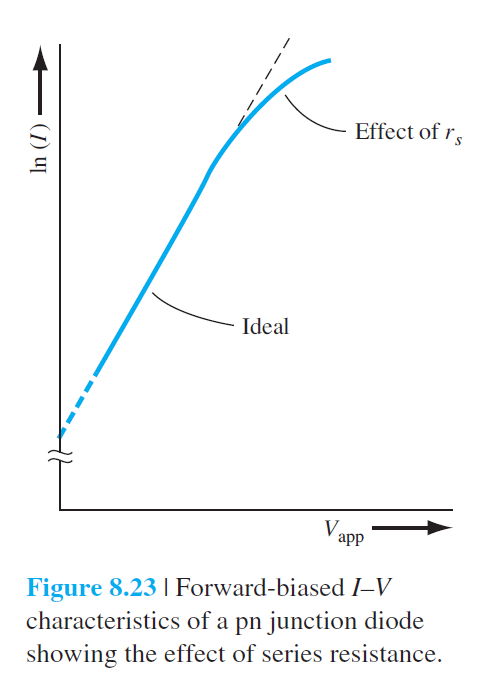
\begin{equation} V_{\text {app }}=V_a+I r_s \qquad (8.106) \end{equation}
8.4 전하축적 및 다이오드이 일시적 특성
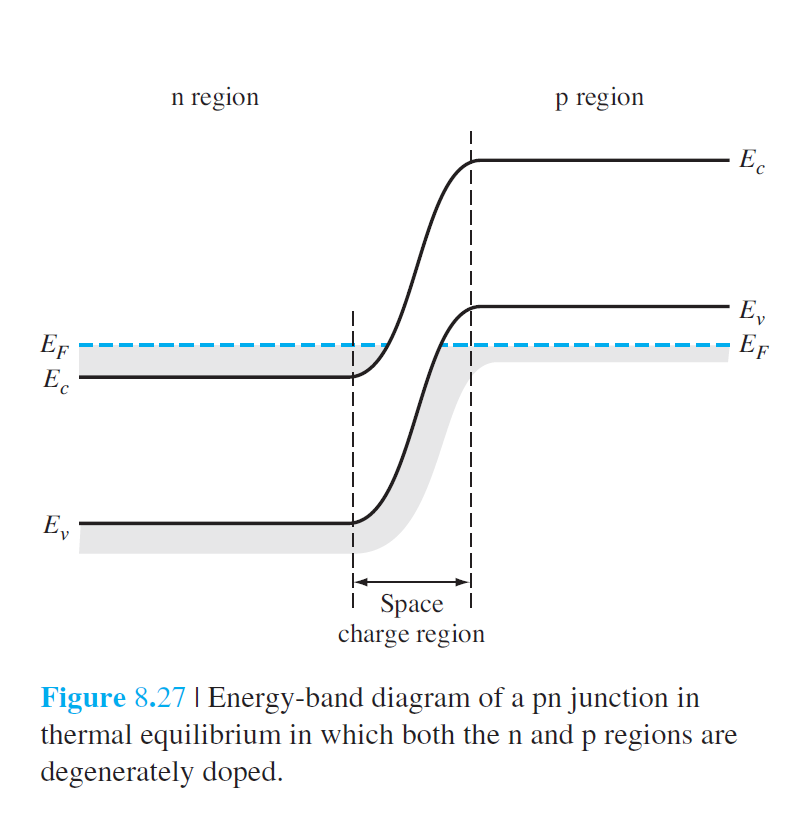
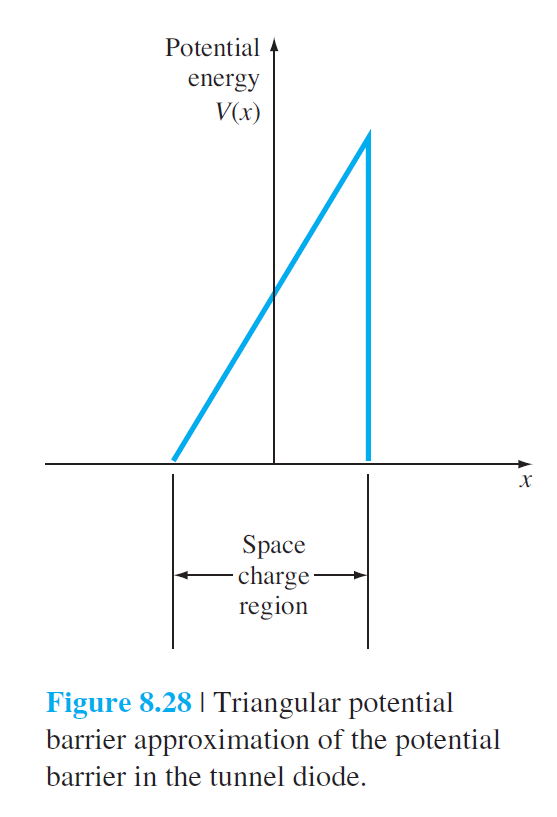
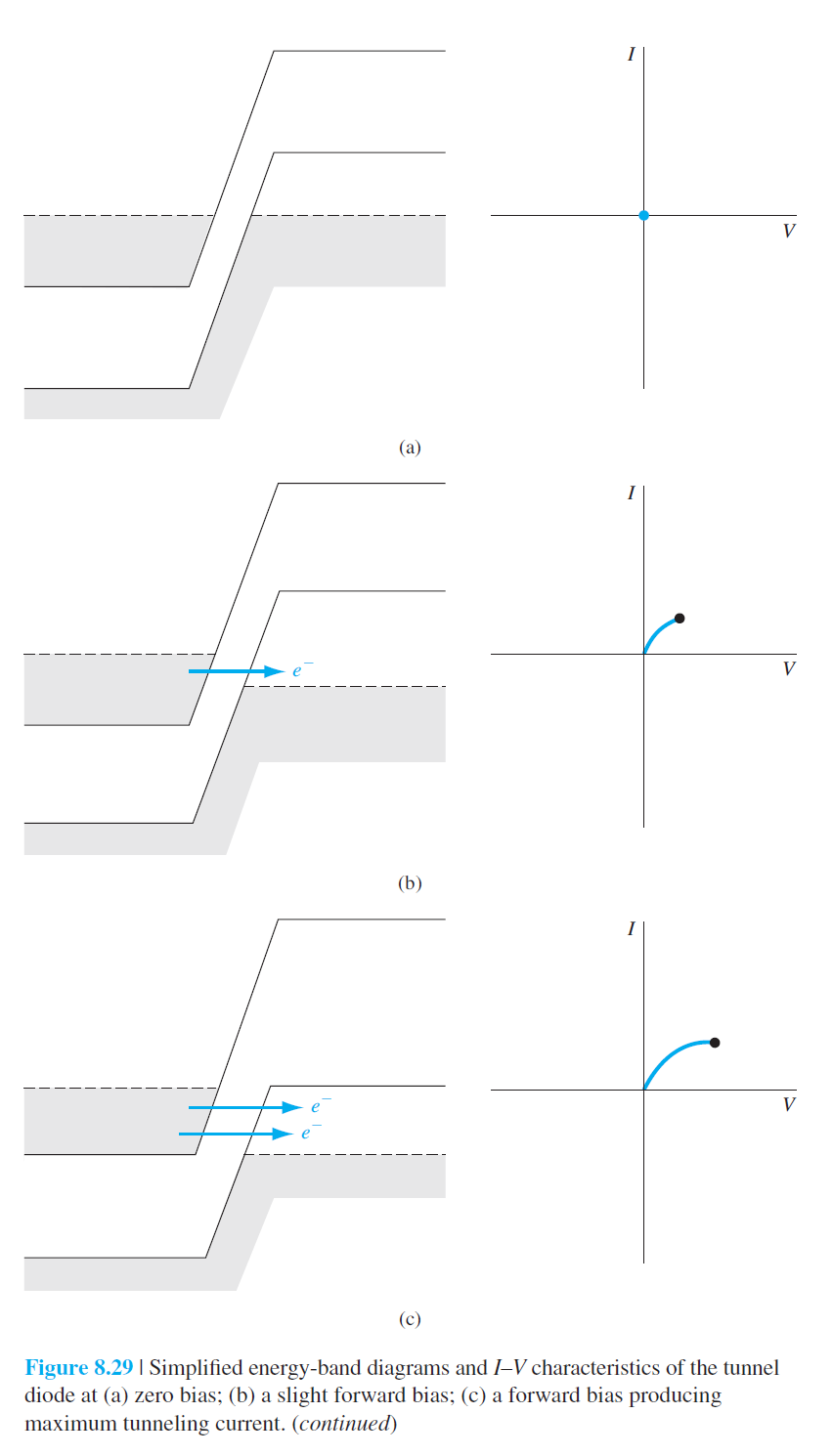
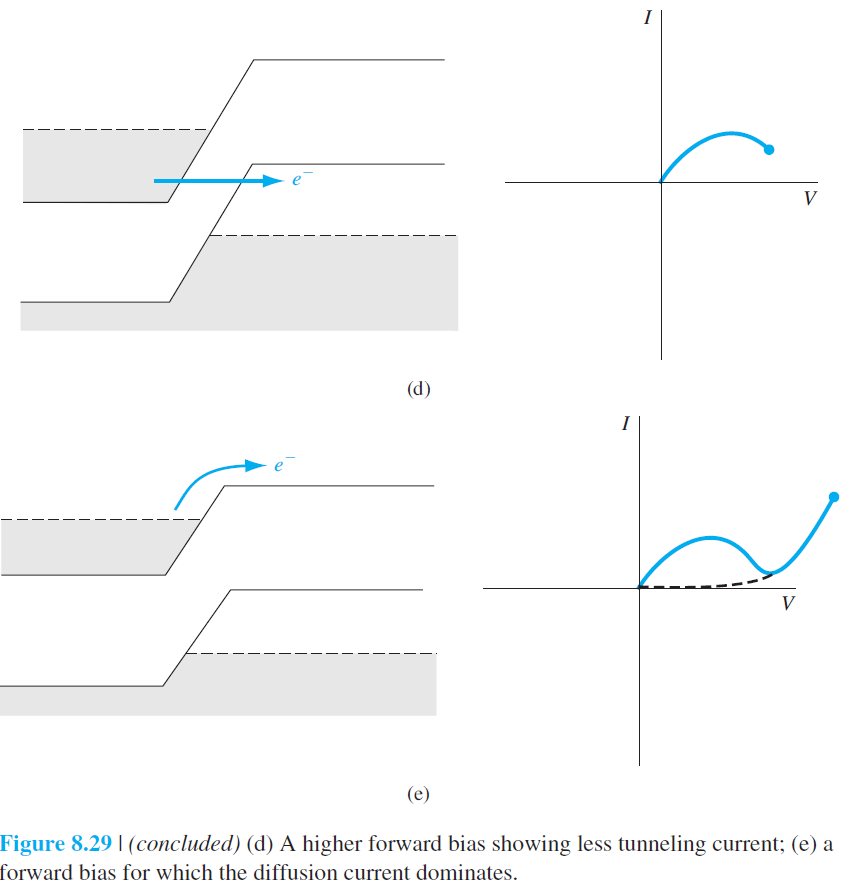
8.5 터널 다이오드