8. 자성체
8.1 자화(Magnetization)
7장에서 보았다시피, 회로가 공간의 어떤 지점에 만드는 자기장은 Biot-Savart 법칙으로 구할 수 있다.
그런데 그 지점이 물질로 채워져있다면, 그 지점에서의 자기장은 순수하게 회로가 만드는 자기장과는 다른 값을 가지게 된다.
이것은 물질이 회로가 만드는 자기장에 반응하여 자체적으로 추가적인 자기장을 생성하기 때문이다.
물질이 자기장을 생성하는 이유는 물질을 이루고 있는 원자의 구조 때문이다.
원자는 양전하인 핵과 그 주위를 돌고있는 음전하의 전자로 이루어져 있는데,
핵 주위로 전자가 돌고있다는 사실은 전자가 하나의 회로를 형성하고 있다는 것을 의미한다.
전자자신도 자체적으로 자전하는 효과가 있어 이 또한 자기장을 생성하는 요인이 된다.
물질에 의한 자기장의 요인은 다음 두가지로 요약된다.
-핵주위로의 전자의 공전
-전자의 자전
여기서 전자의 자전을 spin이라고 한다.
위 요인들에 의한 전류를 회로에 의한 (관습적) 전류와 구분하여 원자적 전류라고 표현할 수 있다.
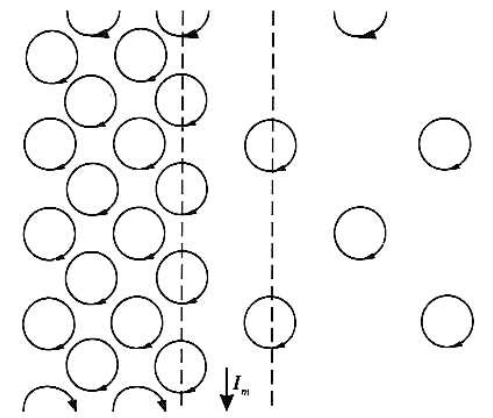
물질내에 i번째 원자가 각각이 원자적 전류를 생성하고, 그에 대응되는 자기쌍극자 모먼트 $\vec{m}_i$가 정의될 수 있다.
그런데 이 원자수준의 자기모먼트 $\vec{m}_i$는 거시적으로 측정되기는 매우 어렵다.
거시적으로 물질의 자성을 평가할 수 있는 양인 자화(magnetization) $\vec{M}$를 다음과 같이 정의할 수 있다.
\begin{equation}
\vec{M}=\lim _{\Delta v \rightarrow 0} \frac{1}{\Delta v} \sum_i \vec{m}_i
\end{equation}
자화의 단위는 A/m이다.
위 식에서 정의된 $\Delta v$는 매우 작은 부피를 의미하며,
위치마다 다른 자화값을 정의할 수 있음을 의미한다.
즉, 자화 $\vec{M}$은 위치의 함수로 표현된다.
7장에서 배운 바에 의하면, 전류고리가 자기장을 생성하며,
전류고리에 대응되는 자기 모먼트를 정의할 수 있다.
자화 또한 자기장을 생성하는 요인이 되므로,
자화에 대응되는 전류밀도를 정의할 수 있음을 의미한다.
자화에 대응되는 전류밀도를 자화 전류밀도(magnetization current density)라고 한다.
• 자화와 자화 전류밀도와의 관계
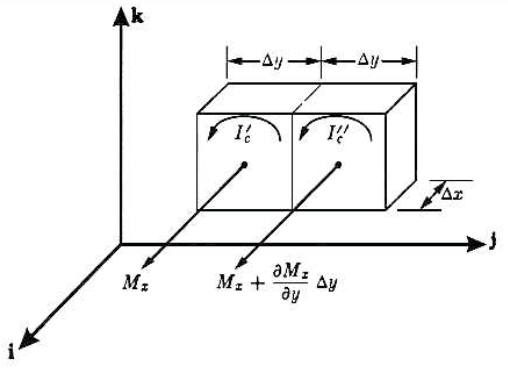
그림과 같이 $y$방향으로 인접한 두 개의 작은 부피 요소를 생각하자.
각 부피요소의 부피는 $\Delta x \Delta y \Delta z$이고,
각각 $I_c'$과 $I_c''$의 전류가 흐른다.
좌측 부피 요소의 자화를 $\vec{M}(x, y, z)$라고 하면,
우측의 인접한 부피요소의 자화는 다음과 같이 주어진다.
\begin{equation}
\vec{M}(x, y, z)+\frac{\partial \vec{M}}{\partial y} \Delta y+\text { 고차수항들 }
\end{equation}
좌측 부피 요소의 자기모먼트의 $x$성분은 어래와 같이 기술할 수 있다.
\begin{equation}
M_x \Delta x \Delta y \Delta z=I_c^{\prime} \Delta y \Delta z
\end{equation}
우측 부피 요소의 자기모먼트의 $x$성분은 어래와 같이 기술할 수 있다.
$$
\left(M_x+\frac{\partial M_x}{\partial y} \Delta y\right) \Delta x \Delta y \Delta z=I_c^{\prime \prime} \Delta y \Delta z .
$$
두 부피요소의 중간 지점에서의 순 전류값은 다음과 같다.
$$
I_c^{\prime}-I_c^{\prime \prime}=-\frac{\partial M_x}{\partial y} \Delta x \Delta y .
$$
만약, $x$방향으로 인접한 두 개의 작은 부피 요소를 고려햇다면,
그 두 부피 요소 사이 지점에서의 순 전류량은 다음과 같다.
$$
\left(I_c\right)_{u p}=\frac{\partial M_y}{\partial x} \Delta x \Delta y .
$$
그러면 $z$방향으로의 전류밀도는 다음과 같다.
$$
\begin{aligned}
\left(J_M\right)_z =\frac{\partial M_y}{\partial x}-\frac{\partial M_x}{\partial y} \\
\end{aligned}
$$
결과적으로 자화와 자화 전류밀도와의 관계는 다음과 같이 얻어진다.
$$
\vec{J}_M =\nabla \times \vec{M}
$$
자화 전류밀도는 자화의 curl로 얻어진다.
8.2 자성체에 의한 자기장
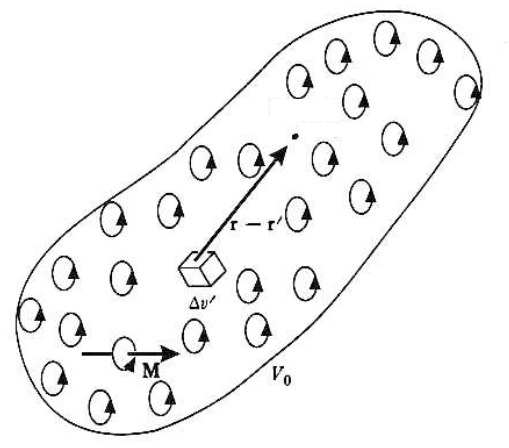
7장에서 자기모먼트 $\vec{m}$에 의한 벡터 포텐셜은 다음과 같이 주어진다고 하였다.
$$
\vec{A}\left(\vec{r}_2\right)=\frac{\mu_0}{4 \pi} \frac{\vec{m} \times \vec{r}_2}{r_2^3}
$$
우리의 관심사는 어떤 부피를 가진 자성체에 의한 자기장을 구하는 것이다.
이 자성체를 잘게 분할하여 분할된 부피요소 $\Delta v'$에 대응되는 자기 모먼트는 다음과 같이 자화로 기술이 가능하다.
$$
\Delta \vec{m}=\vec{M}\left(x^{\prime}, y^{\prime}, z^{\prime}\right) \Delta v^{\prime}
$$
이 요소에 의한 벡터 포텐셜은 다음과 같을 것이다.
$$
\begin{aligned}
d\vec{A}(x, y, z) =\frac{\mu_0}{4 \pi} \frac{\vec{M}\left(x^{\prime}, y^{\prime}, z^{\prime}\right) \times\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime}
\end{aligned}
$$
그러면 자성체에 의한 벡터 포텐셜은 다음과 같이 주어진다.
$$
\begin{aligned}
\vec{A}(x, y, z) & =\frac{\mu_0}{4 \pi} \int_{V_0} \frac{\vec{M}\left(x^{\prime}, y^{\prime}, z^{\prime}\right) \times\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime} \\
& =\frac{\mu_0}{4 \pi} \int_{V_0} \vec{M}\left(x^{\prime}, y^{\prime}, z^{\prime}\right) \times \nabla^{\prime} \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|} d v^{\prime} .
\end{aligned}
$$
위 식은 다음과 같이 두 개의 항으로 기술될 수 있다.
$$
\vec{A}(x, y, z)=\frac{\mu_0}{4 \pi} \int_{\vec{V}_0} \frac{\nabla^{\prime} \times \vec{M}}{\left|\vec{r}-\vec{r}^{\prime}\right|} d v^{\prime}+\frac{\mu_0}{4 \pi} \int_{S_0} \frac{\vec{M} \times \hat{n}}{\left|\vec{r}-\vec{r}^{\prime}\right|} d a^{\prime},
$$
여기서 다음과 같은 표면 자화전류밀도(surface magnetization current density)를 정의하면,
$$
\vec{j}_M=\vec{M} \times \hat{n},
$$
벡터 포텐셜은 다음과 같이 기술될 수 있다.
$$
\vec{A}(\vec{r})=\frac{\mu_0}{4 \pi} \int_{V_0} \frac{\vec{J}_M\left(\vec{r}^{\prime}\right) d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\frac{\mu_0}{4 \pi} \int_{S_0} \frac{\vec{j}_M d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|} .
$$
위 식에서 부피 적분은 실제 전류에 의한 벡터포텐셜과 같은 형태이다.
자성체의 $\vec{B}(\vec{r})$를 구하기 위해,
$\vec{B}(\vec{r}) =\nabla \times \vec{A}$과 위 벡터 포텐셜을 이용하면 되지만,
위 식은 실제적으로 $\vec{B}(\vec{r})$를 구하기는 어려운 표현이다.
자기장을 구하기 쉬운 다른 표현을 구해 본다.
우선 $\vec{B}(\vec{r}) =\nabla \times \vec{A}$ 이 식을 적용해 보면, 다음을 얻는다.
$$
\begin{aligned}
\vec{B}(\vec{r}) & =\nabla \times \vec{A} \\
& =\frac{\mu_0}{4 \pi} \int_{V_0} \nabla \times\left[\vec{M} \times \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right] d v^{\prime},
\end{aligned}
$$
$$
\begin{aligned}
&\nabla \times(\vec{F} \times \vec{G}) \\
&=(\nabla \cdot \vec{G}) \vec{F}-(\nabla \cdot \vec{F}) \vec{G}+(\vec{G} \cdot \nabla) \vec{F}-(\vec{F} \cdot \nabla) \vec{G}
\end{aligned}
$$
위 식을 이용하면, 다음을 얻는다.
$$
\begin{aligned}
&\nabla \times\left[\vec{M} \times \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right] \\
&=\vec{M} \nabla \cdot\left[\frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right]-(\vec{M} \cdot \nabla) \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}
\end{aligned}
$$
\begin{equation}
\end{equation}
결과적으로 자기유도는 다음과 같이 얻어진다.
$$
\vec{B}(\vec{r})=\vec{B}_I(\vec{r})+\vec{B}_{II}(\vec{r}),
$$
위 식에서 $\vec{B}_I$와 $\vec{B}_{II}$는 다음과 같이 주어진다.
$$
\begin{aligned}
& \vec{B}_I(\vec{r})=\frac{\mu_0}{4 \pi} \int_{V_0} \vec{M} \nabla \cdot\left[\frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right] d v^{\prime}, \\
& \vec{B}_{II}(\vec{r})=-\frac{\mu_0}{4 \pi} \int_{V_0}(\vec{M} \cdot \nabla) \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime} .
\end{aligned}
$$
$\vec{B}_I$는 다음과 같이 간소화된다.
$$
\begin{aligned}
\vec{B}_I(\vec{r}) & =\frac{\mu_0}{4 \pi} \int_{V_0} \vec{M}\left(\vec{r}^{\prime}\right) 4 \pi \delta\left(\vec{r}-\vec{r}^{\prime}\right) d v^{\prime} \\
& =\mu_0 \vec{M}(\vec{r})
\end{aligned}
$$
$\vec{B}_{II}$는 다음 관계들에 의하여
$$
\begin{aligned}
&\nabla\left[\vec{M} \cdot \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right] \\
&=(\vec{M} \cdot \nabla) \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}+\vec{M} \times \nabla \times\left[\frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right]
\end{aligned}
$$
$$
\nabla \times\left[\frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3}\right]=-\nabla \times \nabla \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|},
$$
다음과 같이 표현된다.
$$
\vec{B}_{II}(\vec{r})=-\mu_0 \nabla \frac{1}{4 \pi} \int_{V_0} \vec{M}\left(\vec{r}^{\prime}\right) \cdot \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime},
$$
$$
\vec{B}_{II}(\vec{r})=-\mu_0 \nabla \varphi^*(\vec{r})
$$
여기서 다음과 같이 주어지는 $\varphi^*(\vec{r})$는 자성체에 의한 자기 스칼라 포텐셜이라고 한다.
$$
\varphi^*(\vec{r})=\frac{1}{4 \pi} \int_{V_0} \vec{M}\left(\vec{r}^{\prime}\right) \cdot \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime} .
$$
간소화된 식들을 정리하면 자성체에 의한 자기유도는 다음과 같이 주어진다.
$$
\vec{B}(\vec{r})=-\mu_0 \nabla \varphi^*(\vec{r})+\mu_0 \vec{M}(\vec{r})
$$
8.3 자극밀도
다음 식을 이용하면,
\begin{equation}
\begin{aligned}
\frac{\vec{M} \cdot\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} & =\vec{M} \cdot \nabla^{\prime} \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|} \\
& =\nabla^{\prime} \cdot \frac{\vec{M}}{\left|\vec{r}-\vec{r}^{\prime}\right|}-\frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|} \nabla^{\prime} \vec{M}
\end{aligned}
\end{equation}
자성체에 의한 자기 스칼라 포텐셜은 다음과 같이 기술될 수 있다.
$$
\varphi^*(\vec{r})=\frac{1}{4 \pi} \int_{S_0} \frac{\vec{M} \cdot \hat{n} d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}-\frac{1}{4 \pi} \int_{V_0} \frac{\nabla^{\prime} \cdot \vec{M}}{\left|\vec{r}-\vec{r}^{\prime}\right|} d v^{\prime},
$$
위 식에서 적분내의 항들을 다음과 같이 자극밀도(magnetic pole density)로 정의하면,
$$
\rho_M\left(\vec{r}^{\prime}\right) \equiv-\nabla^{\prime} \cdot \vec{M}\left(\vec{r}^{\prime}\right),
$$
$$
\sigma_M\left(\vec{r}^{\prime}\right) \equiv \vec{M}\left(\vec{r}^{\prime}\right) \cdot \hat{n},
$$
자성체에 의한 자기 스칼라 포텐셜은 다음과 같이 자극 밀도로 기술될 수 있다.
$$
\varphi^*(\vec{r})=\frac{1}{4 \pi} \int_{V_0} \frac{\rho_M d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\frac{1}{4 \pi} \int_{S_0} \frac{\sigma_M d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|},
$$
$\rho_M\left(\vec{r}^{\prime}\right)$과 $\sigma_M\left(\vec{r}^{\prime}\right)$는
각각 $\vec{r}^{\prime}$에서의 자극밀도(magnetic pole density)와 자극세기의 표면밀도(surface density of magnetic pole strength)이며,
단위는 각각 A/m$^2$과 A/m이다.
모든 자석의 전체 자극세기는 0이다. 이것은 다음과 같이 표현된다.
$$
\int_{V_0}(-\nabla \cdot \vec{M}) d v+\int_{S_0} \vec{M} \cdot \hat{n} d a=0 .
$$
자기 스칼라 포텐셜이 주어지면, 자기유도는 다음과 같이 얻어진다.
\begin{equation}
\begin{aligned}
\vec{B}(\vec{r}) &= \frac{\mu_0}{4 \pi} \int_{V_0} \rho_M \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime} \\
&+\frac{\mu_0}{4 \pi} \int_{S_0} \sigma_M \frac{\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d a^{\prime}+\mu_0 \vec{M}(\vec{r})
\end{aligned}
\end{equation}
$$
$$
8.4 자기세기
저성체외에 전류밀도 $\vec{J}$로 주어지는 회로가 추가적으로 존재한다면, 위치 $\vec{r}$에서의 자기유도는 다음과 같이 회로에 의한 자기장과 자성체에 의한 자기장의 합으로 주어진다. $$ \begin{gathered} \vec{B}(\vec{r})=\frac{\mu_0}{4 \pi} \int_V \frac{\vec{J} \times\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime}-\mu_0 \nabla \varphi^*(\vec{r})+\mu_0 \vec{M}(\vec{r}) \end{gathered} $$ 여기서 $\varphi^*(\vec{r})$는 다음과 같이 주어진다. $$ \varphi^*(\vec{r})=\frac{1}{4 \pi} \int_V \frac{\rho_M d v^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\frac{1}{4 \pi} \int_S \frac{\sigma_M d a^{\prime}}{\left|\vec{r}-\vec{r}^{\prime}\right|} $$ 자기유도를 구성하는 성분 중에서, 물질의 자성을 표현하는 자화를 제외한 나머지 부분을 다음과 같이 $\vec{H}(\vec{r})$로 정의하면, $$ \vec{H}(\vec{r})=\frac{1}{4 \pi} \int_V \frac{\vec{J} \times\left(\vec{r}-\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|^3} d v^{\prime}-\nabla \varphi^*(\vec{r}) . $$ $\vec{H}(\vec{r})$는 다음과 같이 주어진다. $$ \vec{H}=\frac{1}{\mu_0} \vec{B}-\vec{M} $$ $\vec{H}(\vec{r})$는 자기세기(magnetic intensity)라고 하며, 단위는 자화와 동일하게 A/m이다.
8.5 자기장 방정식
7장에서 자기유도의 다음과 같은 미분 관계식들을 얻었다.
$$
\nabla \cdot \vec{B}=0, \quad \nabla \times \vec{B}=\mu_0 \vec{J}
$$
위 첫째식은 자기홀극이 없다는 뜻이고, 둘째 식은 Ampere법칙의 미분형이다.
자성체가 있는 상황에서는 Ampere법칙의 미분형에서 다음과 같이 우변에 자화전류밀도를 포함시켜야 한다.
$$
\nabla \times \vec{B}=\mu_0\left(\vec{J}+\vec{J}_M\right),
$$
자화를 좌변으로 이동하고, $\vec{J}_M =\nabla \times \vec{M}$을 이용하면,
다음 식이 얻어진다.
$$
\nabla \times\left(\frac{1}{\mu_0} \vec{B}-\vec{M}\right) = \vec{J},
$$
$$
\nabla \times \vec{H}=\vec{J} .
$$
결과적으로 $\vec{H}$는 실제 회로에 의한 전류에 의한 자기장을 표현하고 있고,
물질에 의한 자기장은 반영하고 있지않다.
이것은 전기장의 $\vec{D}$와 유사한 측면이 있다.
위 식의 면적분은 다음과 같이, 전개되어
$$
\begin{aligned}
\int_S \nabla \times \vec{H} \cdot \hat{n} d a & =\oint_C \vec{H} \cdot d \vec{\ell} \\
& =\int_S \vec{J} \cdot \hat{n} d a,
\end{aligned}
$$
다음식이 얻어진다.
$$
\oint_{C} \vec{H} \cdot d \vec{\ell}=I .
$$
즉, $\vec{H}$의 경로방향 성분의 적분은 그 경로를 관통하는 실제 전류와 같다.
$\nabla \cdot \vec{B}=0$의 적분형은 다음과 같이 기술될 수 있다.
$$
\oint_S \vec{B} \cdot \hat{n} d a = 0
$$
즉, 페곡면을 통과하는 자기다발은 0이 된다.
8.6 자화율
자화 $\vec{M}$은 $\vec{H}$에 대한 물질의 반응이므로, 이 두 양사이에 어떤 관계가 성립될 수 있다.
어떤 물질에 대해서는 $\vec{M}$와 $\vec{H}$가 다음과 같은 선형성을 가지는 것으로 관찰된다.
$$
\vec{M}=\chi_m \vec{H}
$$
위 식에서 $\chi_m$을 자화율(magnetic susceptibility)이라고 한다.
$\chi_m > 0$인 물질을 상자성체(paramagnetic),
$\chi_m < 0$인 물질을 반자성체(diamagnetic) 라고 한다.
일반적으로 상자성체와 반자성체에 대한 $\chi_m(\ll 1)$의 크기는 매우 작다.
$$
\begin{array}{lrr}
Material & \chi_m & \chi_{m, \text { mass }}, \mathrm{m}^3 / \mathrm{kg} \\
\hline
Aluminum & 2.1 \times 10^{-5} & 0.77 \times 10^{-8} \\
Bismuth & -16.4 \times 10^{-5} & -1.68 \times 10^{-8} \\
Copper & -0.98 \times 10^{-5} & -0.11 \times 10^{-8} \\
Diamond & -2.2 \times 10^{-5} & -0.62 \times 10^{-8} \\
Gadolinium chloride \left(\mathrm{GdCl}_3\right) & 603.0 \times 10^{-5} & 133.3 \times 10^{-8} \\
Gold & -3.5 \times 10^{-5} & -0.18 \times 10^{-8} \\
Magnesium & 1.2 \times 10^{-5} & 0.68 \times 10^{-8} \\
Mercury & -2.8 \times 10^{-5} & -0.21 \times 10^{-8} \\
Silver & -2.4 \times 10^{-5} & -0.23 \times 10^{-8} \\
Sodium & 0.84 \times 10^{-5} & 0.87 \times 10^{-8} \\
Titanium & 18.0 \times 10^{-5} & 4.01 \times 10^{-8} \\
Tungsten & 7.6 \times 10^{-5} & 0.40 \times 10^{-8} \\
Carbon dioxide (1 \mathrm{~atm}) & -1.19 \times 10^{-8} & -0.60 \times 10^{-8} \\
Hydrogen (1 atm) & -0.22 \times 10^{-8} & -2.48 \times 10^{-8} \\
Nitrogen (1 \mathrm{~atm}) & -0.67 \times 10^{-8} & -0.54 \times 10^{-8} \\
Oxygen (1 \mathrm{~atm}) & 193.5 \times 10^{-8} & 135.4 \times 10^{-8} \\
\hline
\end{array}
$$
* Data는 Handbook of Chemistry and Physics, 58th edition, CRC Press, Inc., Cleveland, Ohio. 으로 부터 얻어졌다. gaussian (cgs) units
질량 자화율과 몰 자화율은 다음과 같이 정의된다.
$$
\begin{aligned}
& \chi_m=\chi_{m, \text { mass }} d \\
& \chi_m=\chi_{\text {m,molar }} \frac{d}{A}
\end{aligned}
$$
위 식에서 $d$는 질량 밀도, $A$는 분자 질량(molecular weight)이다.
$\vec{M}$와 $\vec{H}$가 선형성을 가진다면,
$\vec{B}$와 $\vec{H}$ 사이에 선형성이 존재한다.
$$
\vec{B}=\mu \vec{H}
$$
위 식에서 계수 $\mu$를 투자율(透磁率, permeability)이라고 하며, 단위는 T$\cdot$m/A이다.
투자율과 자화율 사이에는 다음의 관계가 있다
$$
\mu=\mu_0\left(1+\chi_m\right)
$$
진공 대비 상대 투자율 $K_m$은 다음과 같이 정의된다.
$$
K_m=\frac{\mu}{\mu_0}=1+\chi_m
$$
* Data는 American Institute of Physics Handbook, 3rd edition, McGraw-Hill, New York, 1972으로 부터 얻어졌다.
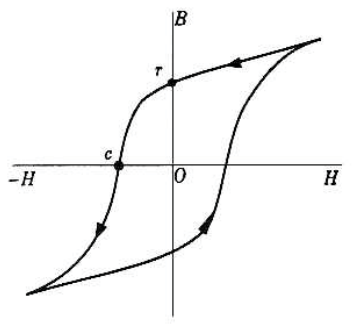
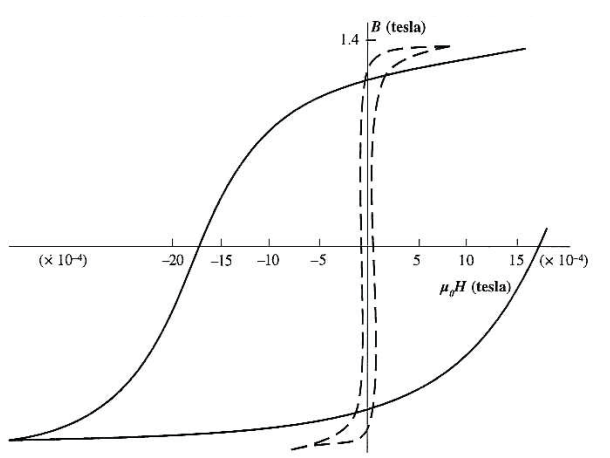
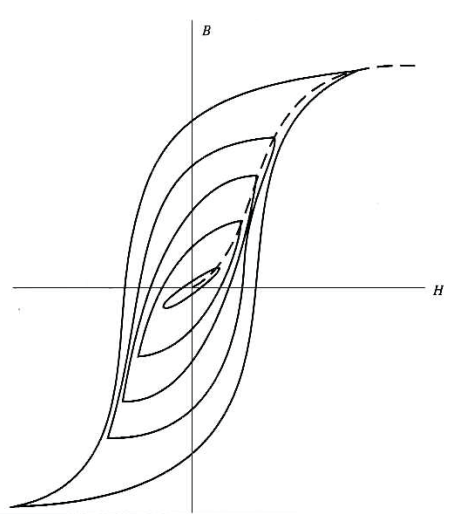
앞서 언급한 상자성체나 반자성체는 $\vec{M}$ 또는 $\vec{B}$가 $\vec{H}$에 선형적인 특성을 나타낸다.
이러한 선형성이 나타나지 않는 자성체도 존재한다.
위 그림처럼 $\vec{B}$가 $\vec{H}$사이에 관계가
자기 이력 곡선(magnetic hysteresis loop)을 나타내는 경우 이 물질을 강자성체(ferromagnetic) 라고 한다.
8.7 경계조건
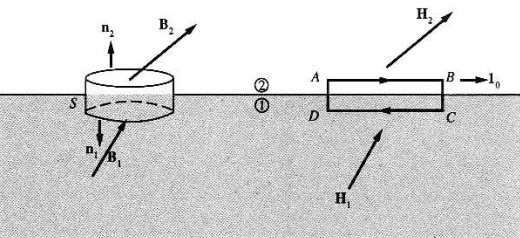
공간에서 매질이 바뀔 때, $\vec{E}$와 $\vec{D}$ 처럼 $\vec{B}$와 $\vec{H}$에 대한 경계조건이 존재한다.
이 들의 경계조건을 얻기 위해 위 그림을 관찰하자.
그림에서 좌측 그림과 같이 경계면에 경계에 걸쳐있는 매우 얇은 (원통형)부피를 생각해 보자.
이 부피에 대해서 다음식을 적용하면
$$
\int_V \nabla \cdot \vec{B} d v = \oint_S \vec{B} \cdot \hat{n} d a = 0
$$
다음 결과를 얻게 된다.
\begin{equation}
\vec{B}_2 \cdot \hat{n}_2 \Delta S+\vec{B}_1 \cdot \hat{n}_1 \Delta S = 0
\end{equation}
$$
\left(\vec{B}_2-\vec{B}_1\right) \cdot \hat{n}_2 = 0
$$
$$
B_{2 n}-B_{1 n} = 0
$$
즉 $\vec{B}$의 수직성분이 연속이 된다.
그림에서 우측 그림과 같이 경계면에 경계에 걸쳐있는 매우 얇은 면를 생각해 보자.
이 면에 대해서 다음 식을 적용하면
$$
\begin{aligned}
\oint_C \vec{H} \cdot d \vec{\ell} =\int_S \vec{J} \cdot \hat{n} d a
\end{aligned}
$$
다음을 얻는다.
$$
\left(\vec{H}_2-\vec{H}_1\right) \cdot \hat{\ell}=\vec{j} \cdot\left(\hat{n}_2 \times \hat{\ell}\right)=\vec{j} \times \hat{n}_2 \cdot \hat{\ell},
$$
$$
\vec{H}_2-\vec{H}_1=\vec{j} \times \hat{n}_2,
$$
$$
\hat{n}_2 \times\left(\vec{H}_2-\vec{H}_{1}\right)=\vec{j}
$$
여기서 $\hat{\ell}$은 $\Delta\vec{\ell}$ 방향의 단위 벡터이고, $\vec{j}$는 표면전하밀도(surface current density)이며, 그 크기는 $I/\Delta\ell$로 주어진다.
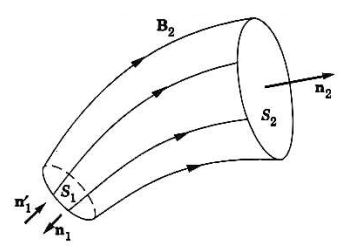
그림과 같이 $\vec{B}$를 따라 형성된 튜브를 고려해보자.
이 튜브에 다음 식을 적용하면
$$
\begin{aligned}
\int_V \nabla \cdot \vec{B} d v & = 0 \\
& =\int_{S_2} \vec{B} \cdot \hat{n} d a-\int_{S_1} \vec{B} \cdot \hat{n}^{\prime} d a \\
& =\Phi\left(S_2\right)-\Phi\left(S_1\right) .
\end{aligned}
$$
위와 같이 튜브의 입구로 들어가는 $\vec{B}$ 다발은 출구로 나오는 $\vec{B}$ 다발과 동일하다는 것을 알수있다.
위 관계는 $\vec{B}$에 적용되고, $\vec{H}$에는 적용되지 않는다.
$$
\int_{s_2} \vec{H} \cdot \hat{n} d a-\int_{s_1} \vec{H} \cdot \hat{n}^{\prime} d a=\int_V \rho_M d v .
$$
위와 같이 튜브의 출구로 나가는 $\vec{H}$ 다발과 입구로 들어가는 $\vec{H}$ 다발과의 차이는
튜브내의 자기 극 세기와 같다는 것을 알수있다.
8.8 경계조건의 적용예
자성체가 있는 공간에 생성된 자기장의 분포를 계산해보자.
회로가 따로 존재하지 않는다고 가정하면 ($\vec{J}=0$), 다음 식들이 성립한다.
$$
\begin{aligned}
\nabla \cdot \vec{B} & =0 \\
\nabla \times \vec{H} & =0 .
\end{aligned}
$$
위 식에서 $\vec{H}$에 대한 식이 의미하는 것은 다음과 같이 $\vec{H}$를 스칼라 포텐셜로 표현할 수 있다는 것을 의미한다.
\begin{equation}
\vec{H}=-\nabla \varphi^*
\end{equation}
우리는 두 종류의 단순한 경계조건 문제를 다룰 것인데,
첫번째는 $\vec{B}=\mu \vec{H}$로 주어지는 선형물질인 경우,
두번째는 $\nabla \cdot \vec{M}=0$으로 주어지는 자화가 균일하게 발생하는 경우이다.
위 두 경우 모두 다음 식을 만족한다.
$$
\nabla \cdot \vec{H} = 0
$$
이것은 스칼라 포텐셜 $\varphi^*$가 다음의 Laplace 방정식을 만족함을 의미한다.
$$
\nabla^2 \varphi^*=0
$$
경계조건을 만족하는 Laplace 방정식의 해인 $\varphi^*$을 구하면,
$\vec{H}$를 구할 수 있고, 아래 식들을 적용하여 $\vec{B}$를 구할 수 있다.
$$
\begin{aligned}
& \vec{B}=\mu \vec{H} \\
& \vec{B}=\mu_0(\vec{H}+\vec{M}),
\end{aligned}
$$
(예제1)
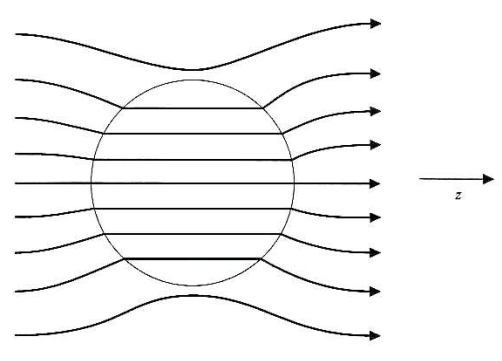
그림과 같이 전공간에 $z$방향으로, $B_0 \hat{k}$의 자기장이 가해지고 있는데,
원점에 반지름이 $a$이고 투자율이 $\mu$인 자성체 공이 있다.
전공간에서 $\vec{B}$를 구해보자.
(풀이)
먼저 Laplace 방정식을 만족하는 스칼라 포텐셜 $\varphi^*$은 그림과 같은 대칭성을 가지는 경우에
zonal harmonics의 형태를 가진 다는 것을 이미 배웠다.
자성체외부의 진공영역을 (1), 자성체 내부영역을 (2)라고, 표기하면
각 영역에서의 스칼라 포텐셜을 다음과 같이 두자.
$$
\varphi_1^*(r, \theta)=A_1 r \cos \theta+C_1 r^{-2} \cos \theta
$$
$$
\varphi_2^*(r, \theta)=A_2 r \cos \theta+C_2 r^{-2} \cos \theta
$$
무한대에서 경계조건 자기장이 $\vec{B} = B_0 \hat{k}$라는 사실을 적용하면,
$\varphi_1^* \rightarrow-\left(B_0 / \mu_0\right) r \cos \theta $을 만족해야 한다.
그러면 계수 $A_1=-\left(B_0 / \mu_0\right)$이 되어야 함을 알 수 있다.
$r=0$에서는 자기장이 무한대가 될수는 없으므로, $C_2$는 0이 되어야 한다.
자성체 표면($r=a$)에서의 경계조건을 적용하기 위해 다음 경계조건을 이용하자.
$$
\begin{aligned}
H_{1 \theta} & =H_{2 \theta}, \\
B_{1 r} & =B_{2 r},
\end{aligned}
$$
그러면 다음 식이 얻어진다.
$$
\begin{aligned}
& -\left(\frac{B_0}{\mu_0}\right) \sin \theta+\frac{C_1}{a^3} \sin \theta=A_2 \sin \theta \\
& B_0 \cos \theta+2 \mu_0 \frac{C_1}{a^3} \cos \theta=-\mu A_2 \cos \theta
\end{aligned}
$$
위 두 식을 연립하면, 다음과 같이 나머지 계수들을 구할 수 있다.
$$
\begin{aligned}
& A_2=-\frac{3 B_0}{\left(\mu+2 \mu_0\right)}, \\
& C_1=\left[\left(\mu / \mu_0\right)-1\right] \frac{B_0 a^3}{\left(\mu+2 \mu_0\right)},
\end{aligned}
$$
그러면 다음 식들을 구할 수 있다.
$$
\vec{B}_2=\frac{3 B_0 \hat{k}}{1+2\left(\mu_0 / \mu\right)}
$$
$$
\vec{B}_1=B_0 \hat{k}+\left[\frac{\left(\mu / \mu_0\right)-1}{\left(\mu / \mu_0\right)+2}\right]\left(\frac{a}{r}\right)^3 B_0\left(2 \hat{r} \cos \theta+\hat{\theta} \sin \theta\right)
$$
(예제2)
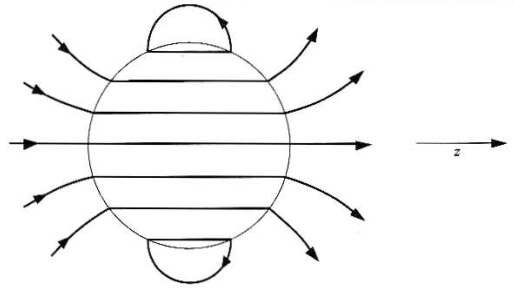
그림과 같이 외부 자기장이 없고, 균일하게 $\vec{M}$으로 자화된 자성체 공이 있다.
전공간에서 $\vec{B}$를 구해보자.
(풀이)
자성체 외부의 진공영역을 (1), 자성체 내부영역을 (2)라고 표기하고,
Laplace 방정식을 만족하는 스칼라 포텐셜 $\varphi^*$를 다음과 같이 두자.
$$
\varphi_1^*(r, \theta)=\sum_{n=0}^{\infty} C_{1, n} r^{-(n+1)} P_n(\theta)
$$
$$
\varphi_2^*(r, \theta)=\sum_{n=0}^{\infty} A_{2, n} r^n P_n(\theta)
$$
자성체 표면에서 다음의 경계조건을 적용하면,
\begin{equation}
\begin{aligned}
H_{1 \theta} & =H_{2 \theta} \\
B_{1 r} & =B_{2 r}
\end{aligned}
\end{equation}
다음 식들이 얻어진다.
$$
\sum_{n=0}^{\infty}\left(C_{1, n} a^{-(n+1)}-A_{2, n} a^n\right) a^{-1} \frac{d}{d \theta} P_n(\theta)=0
$$
또는
\begin{equation}
\sum_{n=0}^{\infty}\left(C_{1, n} a^{-(n+1)}-A_{2, n} a^n\right) P_n(\theta)=\text { 상수 }
\end{equation}
\begin{equation}
\begin{aligned}
&\mu_0 C_{1,0} a^{-2}+\mu_0 \sum_{n=1}^{\infty} P_n(\theta)\left[C_{1, n}(n+1) a^{-(n+2)}+A_{2, n} n a^{n-1}\right]\\
&-\mu_0 M \cos \theta=0
\end{aligned}
\end{equation}
$P_n(\theta)$은 orthogonal하기 때문에 $P_n(\theta)$의 계수들은 모두 사라져야한다.
다음 과정들을 통해, 계수들이 결정되고
$$
\mu_0 C_{1,0} a^{-2}=0 .
$$
$$
C_{1,1} a^{-3}-A_{2,1}=0
$$
$$
2 C_{1,1} a^{-3}+A_{2,1}-M=0,
$$
$$
C_{1,1}=\frac{1}{3} M a^3
$$
$$
A_{2,1}=\frac{1}{3} M \text {. }
$$
아래와 같이 스칼라 포텐셜, $\vec{H}$, $\vec{B}$들이 각각 얻어진다.
$$
\varphi_1^*(r, \theta)=\frac{1}{3} M\left(a^3 / r^2\right) \cos \theta
$$
$$
\varphi_2^*(r, \theta)=\frac{1}{3} M r \cos \theta .
$$
\begin{equation}
\begin{aligned}
& \vec{H}_1=\frac{1}{3} M\left(a^3 / r^3\right)\left[2 \hat{r} \cos \theta+\hat{\theta} \sin \theta\right] \\
& \vec{H}_2=-\frac{1}{3} M \hat{k}
\end{aligned}
\end{equation}
여기서 계수 $\frac{1}{3}$은 다음으로부터 나올 수 있는데
$$ \frac{1}{3}= \frac{1}{4\pi} \frac{4\pi}{3}$$
여기서 $\frac{4\pi}{3}$을 구의 demagnetization factor라고 한다.
자성체 내부의 자기장은 다음과 같이 얻어진다.
$$
\vec{B}_2=\frac{2}{3} \mu_0 M \hat{k}=\frac{2}{3} \mu_0 \vec{M} .
$$
8.9 자성물질을 포함하는 전류 회로
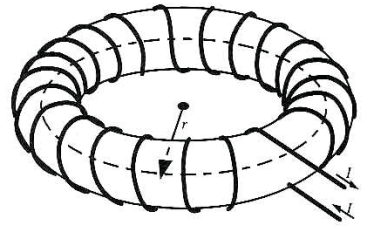
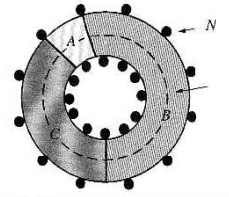
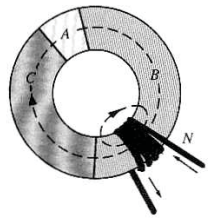
그림과 같은 형상을 toroid라고 한다.
전류 $I$가 흐르는 도선이 총 N번 감겨있고,
그림에서 그려진 점선 경로(길이 $\ell$)에 대해서 Ampere의 법칙을 적용하면,
다음이 얻어진다.
$$
H_t \ell = N I
$$
$$
H_t=\frac{N I}{\ell}
$$
그러면 자기장 $B_t$는 다음과 같이 주어진다.
\begin{equation}
B_t=\frac{\mu_0 N I}{\ell}+\mu_0 M_t
\end{equation}
위 그림은 toroid 내부의 자기장 방향이 왜 경로 방향에 나란한지 보여 주고 있다.
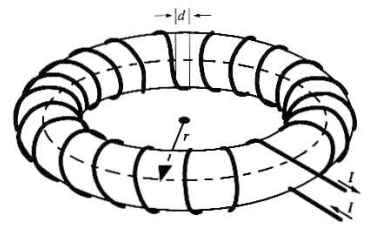
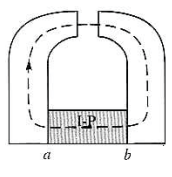
만약 위와 같이 toroid가 자성체를 감싸고 있고,
자성체의 상당히 작은 부분인 $d$만큼이 진공의 틈으로 되어 있을 경우에 toroid 내부의 자기장은 구해볼 것인데
이 경우에는 대칭인 상황이 아니므로,
Ampere 법칙을 그대로 적용할 수 없고, 다음과 같은 절차로 얻을 수 있다.
우선 도선에 의한 $H$는 $H_1$로 표시하고 다음과 같이 얻을 수 있다.
$$
H_1=\frac{N I}{\ell}
$$
도선 자체는 대칭이기 때문에 Ampere 을 그대로 적용할수있다.
이제 자성체에 의해 생성된 자기장이 추가로 존재한다는 것을 주의해야 한다.
자성체가 toroid의 둘레 방향으로 균일하게 자화되었다면, 자성체 내부에서는 자성체에 의한 자화는 0이 될것이다.
그러나 진공인 부분은 자성체의 표면으로 부터 나오는 자기장으로 $H$가 주어지진다는 것을 고려하면,
자성체에 의한 $H$는 다음과 같이 주어진다.
$$
\begin{aligned}
& H_2=M \quad \text { (진공 틈) } \\
& H_2=0 \quad \text { (그외) }
\end{aligned}
$$
위 사실을 고려해서 Ampere법칙을 적용하면 다음과 같이 쓸 수 있는데, 모순이 생기는 것을 확인할 수 있다.
$$
\oint H d \ell = \oint \left(H_1+H_2\right) d \ell = N I+M d \neq N I
$$
그래서 아래와 같이 조정하여 계산하면
$$H_2=M\left(1-\frac{d}{l}\right) \quad \text { (진공 틈) } $$
$$H_2=-M \frac{d}{l} \quad \text { (매질 내부) } $$
Ampere법칙과 B의 연속성을 성립시킬 수 있다.
$$
\begin{gathered}
\vec{B}=\mu_0(\vec{H}+\vec{M}) \\
B=\frac{\mu_0 N I}{l}+\mu_0 M\left(1-\frac{d}{l}\right)
\end{gathered}
$$
자화율만 알면 다음의 관계식으로부터 자기장을 얻을 수 있다.
$$
M=\chi_m(H) H
$$
8.10 자기회로