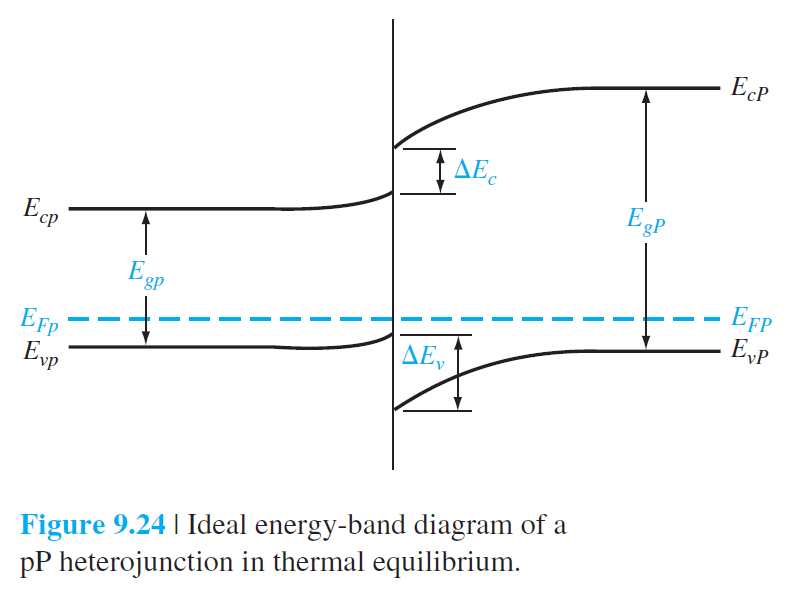
9. 금속-반도체 및 반도체 이종접합
앞 장까지의 내용은 p형 반도체와 n형 반도체의 접합으로 이루어진 소자를 다루었는데,
두 반도체가 동일한 물질로 이루어졌기 때문에 이 접합은 동종접합(homojunction)이라고 한다.
다른 물질의 접합은 이종접합(heterojunction)이라고 한다.
이 장에서는 다른 물질로 이루어진 접합인 금속-반도체 접합과 이 접합에 대한 전류-전압 특성을 공부해 본다.
9.1 Schottky 장벽(barrier) 다이오드
금속-반도체 접합으로 이루어진 이 다이오드는 1900년도 초기에 사용되었으나,
재현성이 좋지 않고, 기계적 신뢰성이 좋지 않아서 1950년대에 PN접합 다이오드로 대체 되었다.
정류성 접촉은 대부분 n형 반도체에서 일어나기 때문에, n형 반도체 접촉을 좀더 많이 알아본다.
9.1.1 정성적 특성들
금속-반도체 접합을 논의하기 전에 몇가지 양에 대한 표기법을 정의하자.
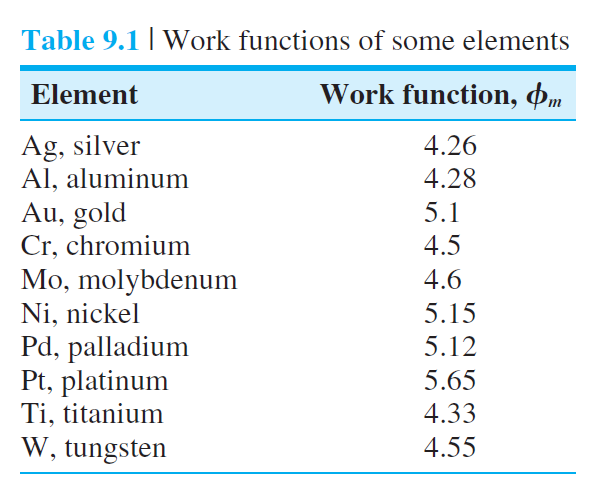
표 9.1에는 금속의 일함수가 표 9.2에는 몇몇 반도체의 전자 친화도가 주어져 있다.

금속과 n형 반도체의 접합을 가정하자. 금속의 일함수가 반도체의 일함수보다 큰 경우($\phi_m > \phi_s$)에 접촉전과 후의 에너지 다이어그램이 그림 9.1(a)와 (b)에 보이고 있다.
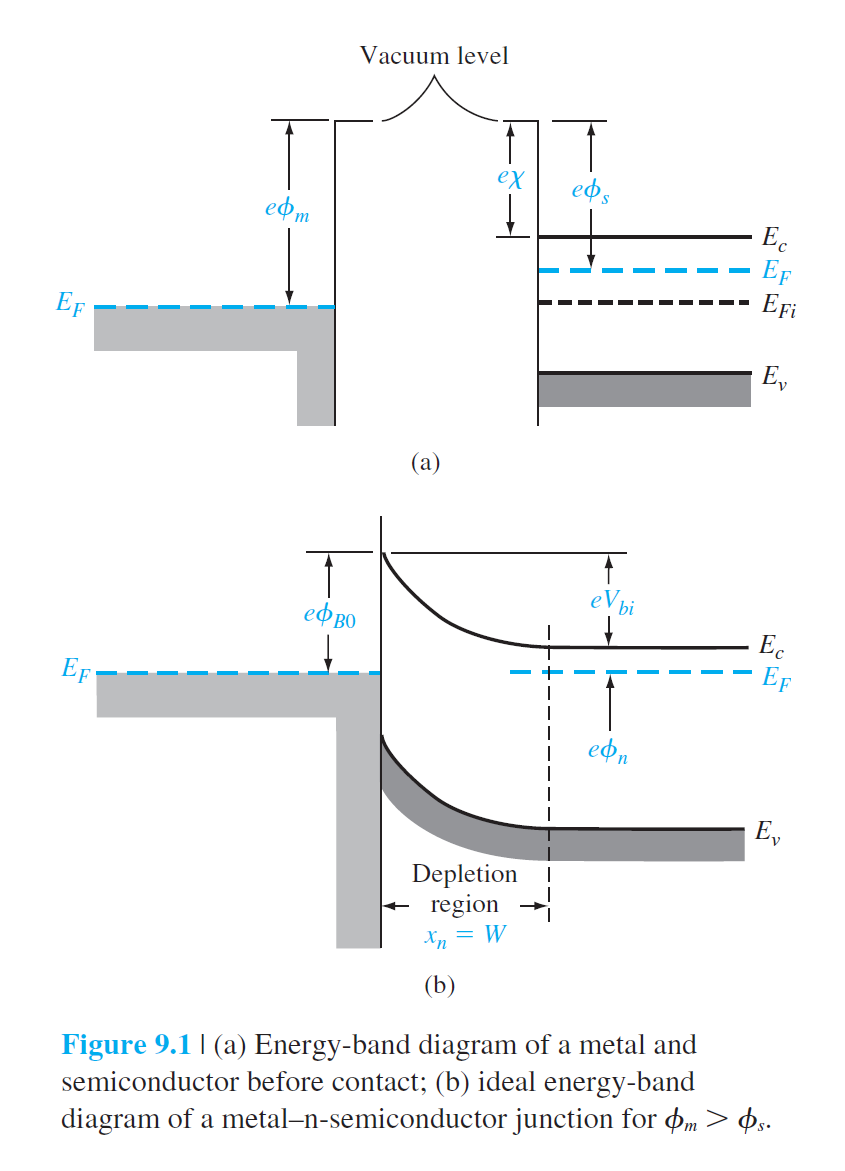
$E_F$는 반도체 쪽이 더 높기 때문에, 전자가 반도체 쪽에서 금속쪽으로 흘러 들어가게 되고 곧 평형이 되면서 $E_F$가 전체적으로 동일한 높이를 유지하게 된다. 이때 다른 특성을 유지시키면서, $E_F$가 동일한 높이가 되기 때문에, 그림 9.1(b)와 같이 에너지 밴드가 휘어지게 된다. $\phi_{B0}$는 전자가 금속에서 반도체로 이동할때 느끼는 이상적인 장벽의 높이이다. 이 장벽을 Schottky 장벽이라고 하며, 이상적으로는 다음과 같이 주어진다. $$ \phi_{B 0}=\left(\phi_m-\chi\right) \qquad (9.1) $$ 전자가 반도체에서 도체로 이동할 때는 $V_{bi}$의 built-in 포텐셜 장벽을 느끼며, 다음과 같이 주어진다. $$ V_{b i}=\phi_{B 0}-\phi_n \qquad (9.2) $$ • 역전압
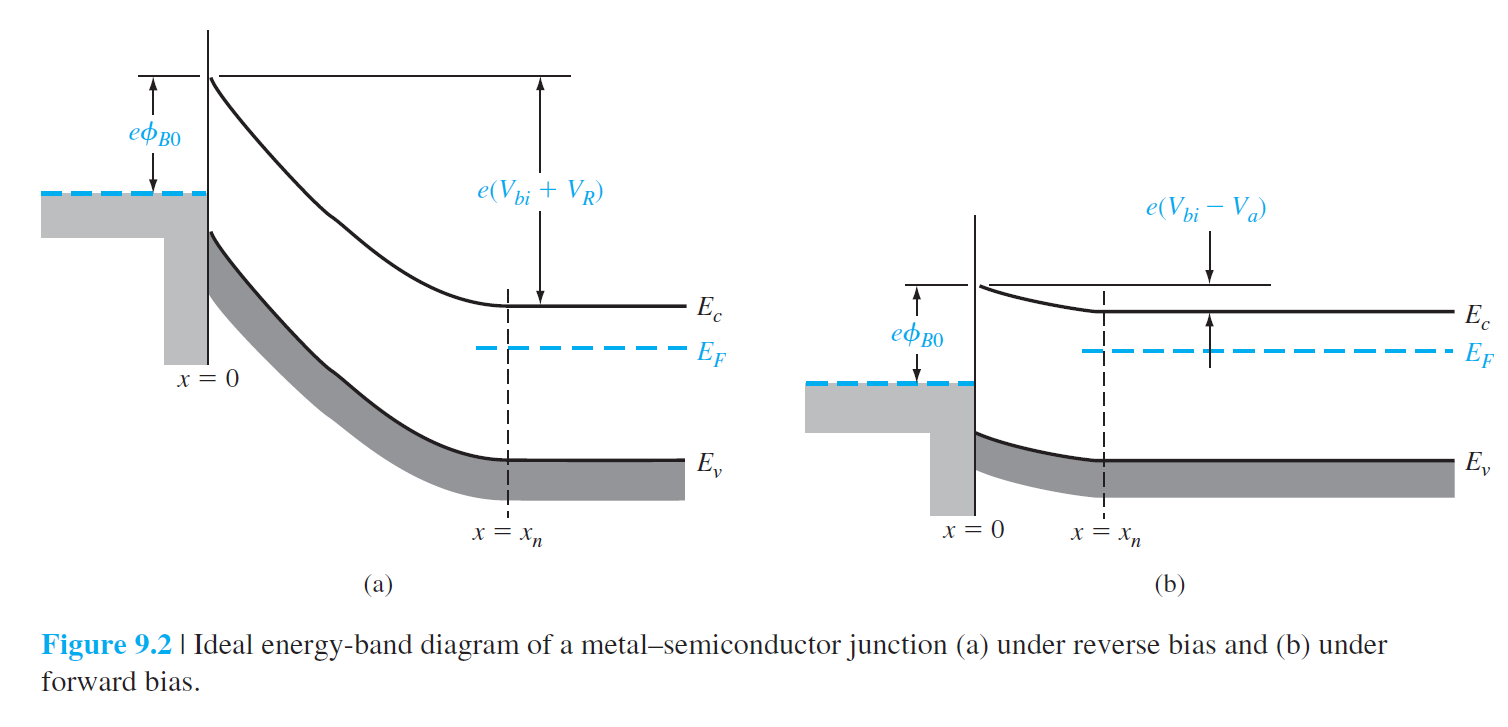
반도체에 양의 전압을 가하는것이 역전압이다. 이 경우 반도체 측의 $E_F$가 하락하고, Schottky 장벽($\phi_{B0}$)은 변함이 없어서, 반도체-금속간 장벽의 높이가 증가한다.
• 순전압
반도체에 음의 전압을 가하는것이 순전압이다. 이 경우 반도체 측의 $E_F$가 상승하고, Schottky 장벽($\phi_{B0}$)은 변함이 없어서, 반도체-금속간 장벽의 높이가 낮아진다.
역전압과 순전압의 경우 에너지 다이어그램이 그림 9.2에 보여진다.
| 기호 | 의미 |
|---|---|
| $\phi_m$ | 금속의 일함수 |
| $\phi_s$ | 반도체의 일함수 |
| $\phi_{B0}$ | 장벽높이(금속 → 반도체, Schottky 장벽) |
| $V_{bi}$ | 장벽높이(반도체 → 금속) |
| $\phi_n$ | $(E_c-E_F)/e$ |
| $\chi$ | 전자 친화도 |


금속과 n형 반도체의 접합을 가정하자. 금속의 일함수가 반도체의 일함수보다 큰 경우($\phi_m > \phi_s$)에 접촉전과 후의 에너지 다이어그램이 그림 9.1(a)와 (b)에 보이고 있다.

$E_F$는 반도체 쪽이 더 높기 때문에, 전자가 반도체 쪽에서 금속쪽으로 흘러 들어가게 되고 곧 평형이 되면서 $E_F$가 전체적으로 동일한 높이를 유지하게 된다. 이때 다른 특성을 유지시키면서, $E_F$가 동일한 높이가 되기 때문에, 그림 9.1(b)와 같이 에너지 밴드가 휘어지게 된다. $\phi_{B0}$는 전자가 금속에서 반도체로 이동할때 느끼는 이상적인 장벽의 높이이다. 이 장벽을 Schottky 장벽이라고 하며, 이상적으로는 다음과 같이 주어진다. $$ \phi_{B 0}=\left(\phi_m-\chi\right) \qquad (9.1) $$ 전자가 반도체에서 도체로 이동할 때는 $V_{bi}$의 built-in 포텐셜 장벽을 느끼며, 다음과 같이 주어진다. $$ V_{b i}=\phi_{B 0}-\phi_n \qquad (9.2) $$ • 역전압
반도체에 양의 전압을 가하는것이 역전압이다. 이 경우 반도체 측의 $E_F$가 하락하고, Schottky 장벽($\phi_{B0}$)은 변함이 없어서, 반도체-금속간 장벽의 높이가 증가한다.
• 순전압
반도체에 음의 전압을 가하는것이 순전압이다. 이 경우 반도체 측의 $E_F$가 상승하고, Schottky 장벽($\phi_{B0}$)은 변함이 없어서, 반도체-금속간 장벽의 높이가 낮아진다.
역전압과 순전압의 경우 에너지 다이어그램이 그림 9.2에 보여진다.

9.1.2 이상적 접합의 특성들
PN 접합에 적용했던 방법을 동일하게 적용하여 정전기적인 특성을 구해보자.
• 전기장
공핍층 내의 전기장은 다음의 Poisson 방정식으로 구할 수 있다. $$ \frac{d E}{d x}=\frac{\rho(x)}{\epsilon_s} \qquad (9.3) $$ 균일한 도핑을 가정한다. $$ E=\int \frac{e N_d}{\epsilon_s} d x=\frac{e N_d x}{\epsilon_s}+C_1 \qquad (9.4) $$ 공핍층의 가장자리는 전기장이 0으로 가정되므로 다음과 같이 상수가 결정된다. $$ C_1=-\frac{e N_d x_n}{\epsilon_s} \qquad (9.5) $$ 결과적으로 공핍층내의 전기장은 다음과 같이 주어진다. $$ E=-\frac{e N_d}{\epsilon_s}\left(x_n-x\right) \qquad (9.6) $$ 공핍층의 폭은 다음과 같이 주어지는데 $p^+n$ 일방접합의 경우와 동일하게 주어진다. $$ W=x_n=\left[\frac{2 \epsilon_s\left(V_{b i}+V_R\right)}{e N_d}\right]^{1 / 2} \qquad (9.7) $$ 여기서 $V_R$은 역방향 전압을 의미한다.
• 접합 전기용량
PN 접합에서의 방법과 유사한 방법으로 접합 전기용량은 다음과 같이 주어진다.
$$ C'=e N_d \frac{d x_n}{d V_R}=\left[\frac{e \epsilon_s N_d}{2\left(V_{b i}+V_R\right)}\right]^{1 / 2} \qquad (9.8) $$ $$ \left(\frac{1}{C'}\right)^2=\frac{2\left(V_{b i}+V_R\right)}{e \epsilon_s N_d} \qquad (9.9) $$ 그림 9.3은 전기용량과 역전압 관계를 보여주며, $V_{bi}$ 등의 정보를 알수있게 한다. 그림 9.3에서는 $V_{bi, \mathrm{GaAs}} > V_{bi, \mathrm{Si}}$ 임을 보여준다.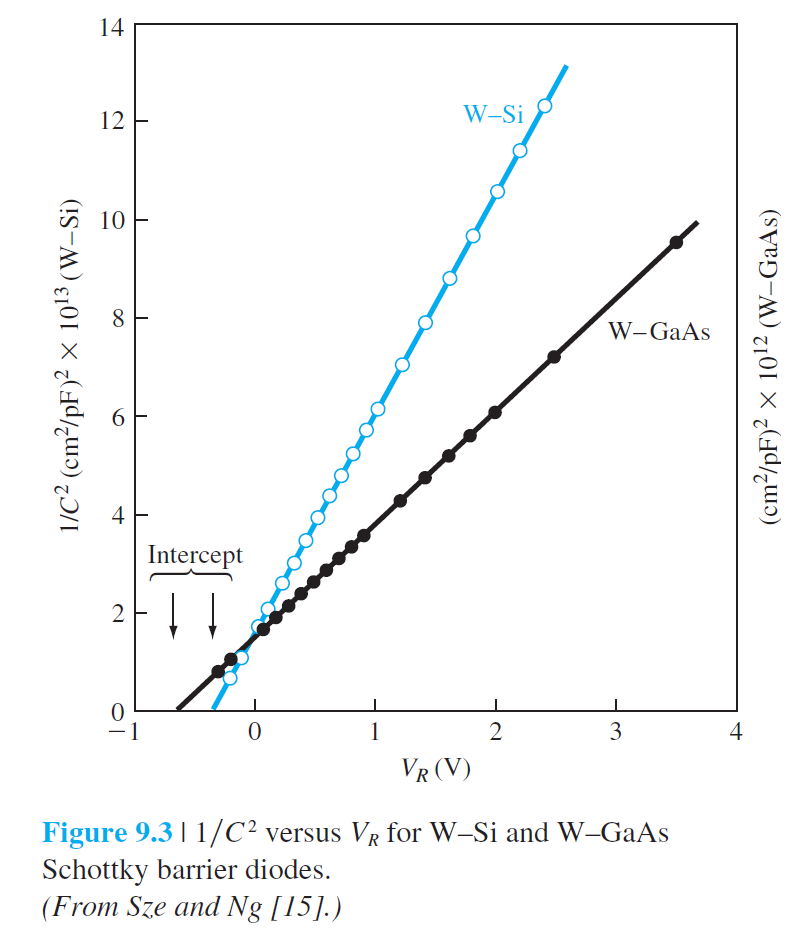

• 전기장
공핍층 내의 전기장은 다음의 Poisson 방정식으로 구할 수 있다. $$ \frac{d E}{d x}=\frac{\rho(x)}{\epsilon_s} \qquad (9.3) $$ 균일한 도핑을 가정한다. $$ E=\int \frac{e N_d}{\epsilon_s} d x=\frac{e N_d x}{\epsilon_s}+C_1 \qquad (9.4) $$ 공핍층의 가장자리는 전기장이 0으로 가정되므로 다음과 같이 상수가 결정된다. $$ C_1=-\frac{e N_d x_n}{\epsilon_s} \qquad (9.5) $$ 결과적으로 공핍층내의 전기장은 다음과 같이 주어진다. $$ E=-\frac{e N_d}{\epsilon_s}\left(x_n-x\right) \qquad (9.6) $$ 공핍층의 폭은 다음과 같이 주어지는데 $p^+n$ 일방접합의 경우와 동일하게 주어진다. $$ W=x_n=\left[\frac{2 \epsilon_s\left(V_{b i}+V_R\right)}{e N_d}\right]^{1 / 2} \qquad (9.7) $$ 여기서 $V_R$은 역방향 전압을 의미한다.

• 접합 전기용량
PN 접합에서의 방법과 유사한 방법으로 접합 전기용량은 다음과 같이 주어진다.
$$ C'=e N_d \frac{d x_n}{d V_R}=\left[\frac{e \epsilon_s N_d}{2\left(V_{b i}+V_R\right)}\right]^{1 / 2} \qquad (9.8) $$ $$ \left(\frac{1}{C'}\right)^2=\frac{2\left(V_{b i}+V_R\right)}{e \epsilon_s N_d} \qquad (9.9) $$ 그림 9.3은 전기용량과 역전압 관계를 보여주며, $V_{bi}$ 등의 정보를 알수있게 한다. 그림 9.3에서는 $V_{bi, \mathrm{GaAs}} > V_{bi, \mathrm{Si}}$ 임을 보여준다.


9.1.3 장벽 높이에서의 비이상적인 효과들
이전 내용들은 이상적인 Schottky 장벽을 다루었고,
실제적으로는 그것에 벗어나는 몇가지 요인들이 있다.
• Schottky 효과(영상전하 효과)
반도체 영역에 있는 전자는 Schottky 장벽 외에, 금속에서 전달되는 영상전하 효과를 추가적으로 느끼게 된다. 이 영상전하 효과는 전자 자신의 존재 때문에 발생하는 것으로 경계 조건이 만족되기 위해서 자연스럽게 발생하게 되며, 실제적으로는 금속 표면 밖으로 거리 $x$ 만큼 떨어저 있는 전하량 $-e$인 전자는 금속 표면 안으로 거리 $x$에 전하량 $+e$인 양(영상)전하가 있는 것처럼 느끼게 된다. 영상전하에 의해 전자가 받는 힘은 다음과 같다. \begin{equation} F=\frac{-e^2}{4 \pi \epsilon_s(2 x)^2}=-e E \qquad (9.10) \end{equation} 포텐셜은 다음과 같다. $$ -\phi(x)=+\int_x^{\infty} E d x'=+\int_x^{\infty} \frac{e}{4 \pi \epsilon_s \cdot 4\left(x'\right)^2} d x'=\frac{-e}{16 \pi \epsilon_s x} \qquad (9.11) $$ 이 포텐셜이 그림 9.4(b)에 보여진다. 영상전하의 효과가 추가되면, 전자가 느끼는 포텐셜은 다음과 같이 주어지며, 그림 9.4(c)에 보여진다. $$ -\phi(x)=\frac{-e}{16 \pi \epsilon_s x}-E x \qquad (9.12) $$ 여기서 반도체에서 밴드의 휘어짐은 거의 선형적이라고 가정된다. 다음과 같이 Schottky 장벽의 감소를 구할 수 있다. $$ \begin{aligned} & \frac{d[e \phi(x)]}{d x} = 0 \qquad (9.13) \\ & x_m = \sqrt{\frac{e}{16 \pi \epsilon_s E}} \qquad (9.14) \\ & \Delta \phi = \sqrt{\frac{e E}{4 \pi \epsilon_s}} \qquad (9.15) \end{aligned} $$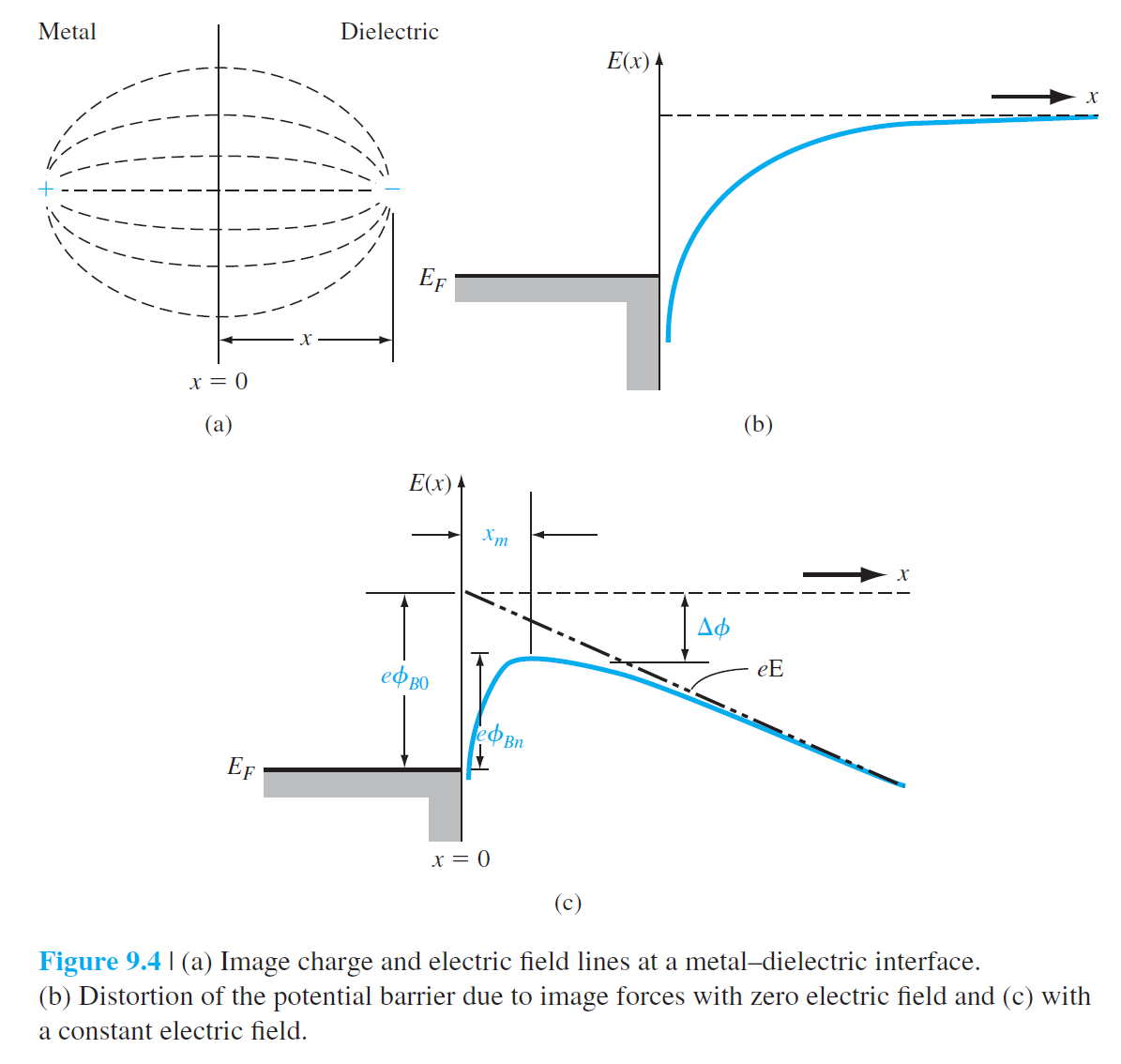

• 경계면 준위
그림 9.5는 몇가지 금속에 대해서 측정된 장벽 높이와 일함수의 관계를 보여준다. (9.1)식에서는 Schottky 장벽의 높이와 일함수가 선형 관계가 있지만, 그림 9.5의 실제 데이터는 완전한 선형관계는 보여주지 못하고 있다. 이러한 현상의 원인 중의 하나는 경계면에 존재하는 불순물 준위(interface states)이다.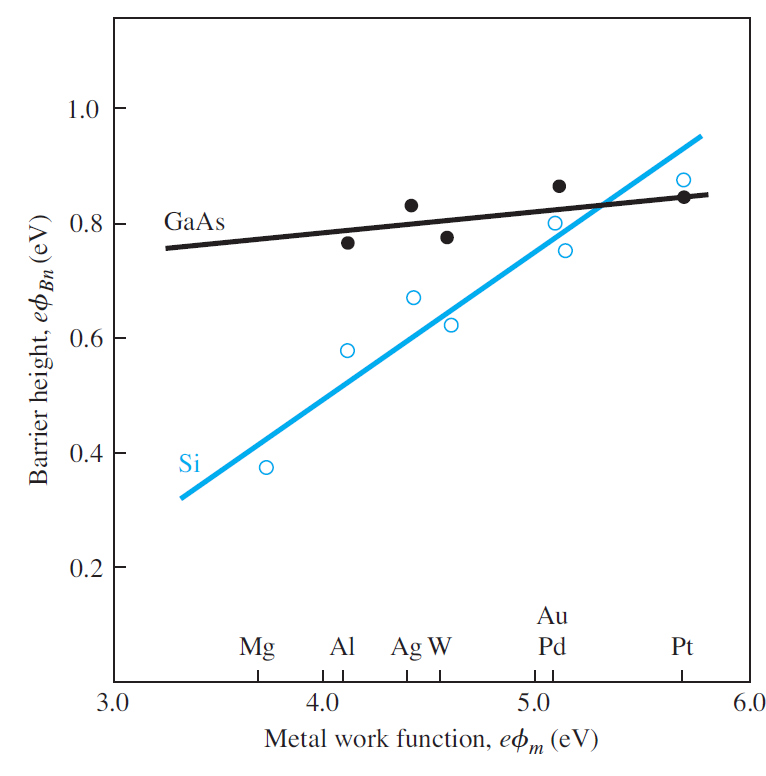
그림 9.6은 금속-n형 반도체 접촉에서 좀더 상세한 에너지 밴드를 보여주고 있다. 여기서 금속과 반도체 사이에 얇은 계면층이 있다고 가정한다. 이 계면층은 절연층으로 보통 산화물(oxides)에 해당한다.
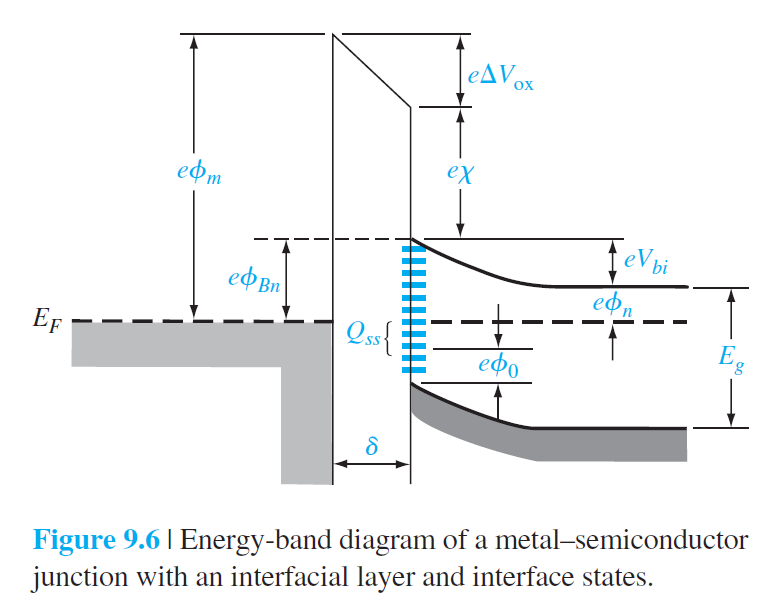
그림에서 주의할 양은 $\phi_0$인데, 중성 준위(표면 준위)라고 불린다. $\phi_0$위의 계면 준위들은 accpeptor 준위, $\phi_0$ 아래의 계면 준위들은 donor 준위라고 가정된다. 표면에서 $E_F$가 어느 계면 준위에 있느냐에 따라 알짜 계면 전하의 타입이 결정되며, 표면에서 $E_F$가 $e\phi_0$와 일치하면 알짜 계면 전하는 0이 된다. 표면 준위 밀도가 $D_{it}$ states/cm$^2$-eV의 어떤 일정한 양으로 주어진다고 하자. 그러면 중성 준위와 관련된 식은 다음과 같다. $$ \begin{aligned} &\left(E_g-e \phi_0-e \phi_{B n}\right) \\ &=\frac{1}{e D_{i t}} \sqrt{2 e \epsilon_s N_d\left(\phi_{B n}-\phi_n\right)}-\frac{\epsilon_i}{e D_{i t} \delta}\left[\phi_m-\left(\chi+\phi_{B n}\right)\right] \qquad (9.16) \end{aligned} $$ 결과적으로 Schottky 장벽은 계면준위와 관련이 있음을 알수있다. 다으 두 극단적인 경우에 Schottky 장벽을 알아보자.
경우 1 : $D_{it} \rightarrow \infty $
$$ \phi_{B n}=\frac{1}{e}\left(E_g-e \phi_0\right) \qquad (9.17) $$ $E_F$가 $\phi_0$에 고정된다.
경우 2 : $D_{it} \delta \rightarrow 0 $
$$ \phi_{B n}=\left(\phi_m-\chi\right) $$ 이것은 이상적인 결과와 일치한다.
• Schottky 효과(영상전하 효과)
반도체 영역에 있는 전자는 Schottky 장벽 외에, 금속에서 전달되는 영상전하 효과를 추가적으로 느끼게 된다. 이 영상전하 효과는 전자 자신의 존재 때문에 발생하는 것으로 경계 조건이 만족되기 위해서 자연스럽게 발생하게 되며, 실제적으로는 금속 표면 밖으로 거리 $x$ 만큼 떨어저 있는 전하량 $-e$인 전자는 금속 표면 안으로 거리 $x$에 전하량 $+e$인 양(영상)전하가 있는 것처럼 느끼게 된다. 영상전하에 의해 전자가 받는 힘은 다음과 같다. \begin{equation} F=\frac{-e^2}{4 \pi \epsilon_s(2 x)^2}=-e E \qquad (9.10) \end{equation} 포텐셜은 다음과 같다. $$ -\phi(x)=+\int_x^{\infty} E d x'=+\int_x^{\infty} \frac{e}{4 \pi \epsilon_s \cdot 4\left(x'\right)^2} d x'=\frac{-e}{16 \pi \epsilon_s x} \qquad (9.11) $$ 이 포텐셜이 그림 9.4(b)에 보여진다. 영상전하의 효과가 추가되면, 전자가 느끼는 포텐셜은 다음과 같이 주어지며, 그림 9.4(c)에 보여진다. $$ -\phi(x)=\frac{-e}{16 \pi \epsilon_s x}-E x \qquad (9.12) $$ 여기서 반도체에서 밴드의 휘어짐은 거의 선형적이라고 가정된다. 다음과 같이 Schottky 장벽의 감소를 구할 수 있다. $$ \begin{aligned} & \frac{d[e \phi(x)]}{d x} = 0 \qquad (9.13) \\ & x_m = \sqrt{\frac{e}{16 \pi \epsilon_s E}} \qquad (9.14) \\ & \Delta \phi = \sqrt{\frac{e E}{4 \pi \epsilon_s}} \qquad (9.15) \end{aligned} $$


• 경계면 준위
그림 9.5는 몇가지 금속에 대해서 측정된 장벽 높이와 일함수의 관계를 보여준다. (9.1)식에서는 Schottky 장벽의 높이와 일함수가 선형 관계가 있지만, 그림 9.5의 실제 데이터는 완전한 선형관계는 보여주지 못하고 있다. 이러한 현상의 원인 중의 하나는 경계면에 존재하는 불순물 준위(interface states)이다.

그림 9.6은 금속-n형 반도체 접촉에서 좀더 상세한 에너지 밴드를 보여주고 있다. 여기서 금속과 반도체 사이에 얇은 계면층이 있다고 가정한다. 이 계면층은 절연층으로 보통 산화물(oxides)에 해당한다.

그림에서 주의할 양은 $\phi_0$인데, 중성 준위(표면 준위)라고 불린다. $\phi_0$위의 계면 준위들은 accpeptor 준위, $\phi_0$ 아래의 계면 준위들은 donor 준위라고 가정된다. 표면에서 $E_F$가 어느 계면 준위에 있느냐에 따라 알짜 계면 전하의 타입이 결정되며, 표면에서 $E_F$가 $e\phi_0$와 일치하면 알짜 계면 전하는 0이 된다. 표면 준위 밀도가 $D_{it}$ states/cm$^2$-eV의 어떤 일정한 양으로 주어진다고 하자. 그러면 중성 준위와 관련된 식은 다음과 같다. $$ \begin{aligned} &\left(E_g-e \phi_0-e \phi_{B n}\right) \\ &=\frac{1}{e D_{i t}} \sqrt{2 e \epsilon_s N_d\left(\phi_{B n}-\phi_n\right)}-\frac{\epsilon_i}{e D_{i t} \delta}\left[\phi_m-\left(\chi+\phi_{B n}\right)\right] \qquad (9.16) \end{aligned} $$ 결과적으로 Schottky 장벽은 계면준위와 관련이 있음을 알수있다. 다으 두 극단적인 경우에 Schottky 장벽을 알아보자.
경우 1 : $D_{it} \rightarrow \infty $
$$ \phi_{B n}=\frac{1}{e}\left(E_g-e \phi_0\right) \qquad (9.17) $$ $E_F$가 $\phi_0$에 고정된다.
경우 2 : $D_{it} \delta \rightarrow 0 $
$$ \phi_{B n}=\left(\phi_m-\chi\right) $$ 이것은 이상적인 결과와 일치한다.
9.1.4 전류-전압 관계
PN 접합에서의 전류는 소수운반자에 기인한것과는 달리
금속-반도체 접합에서의 전류는 다수 운반자에 기인하며,
포텐셜 장벽을 넘어가는 열전자 방출 이론을 통해서 설명될 수 있다.
• 열전자 방출(thermionic emission)
장벽의 높이가 $kT$보다 훨씬 크다는 가정을 통해 Maxwell-Boltzmann 근사 를 이용한다.
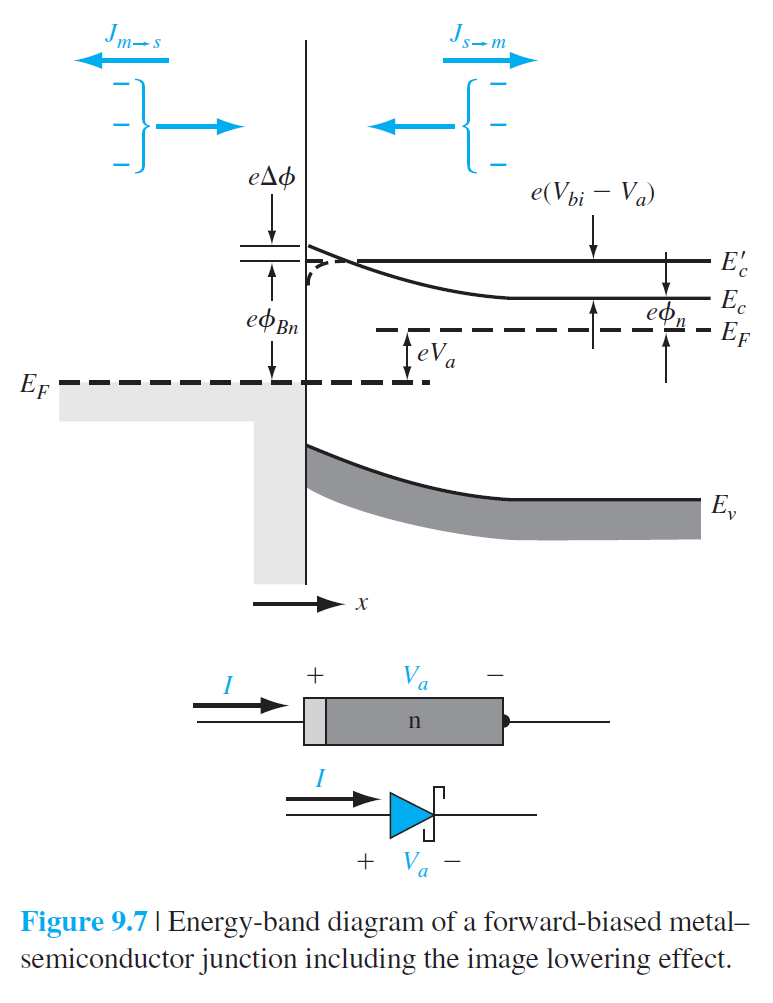
그림 9.7은 순전압 $V_a$가 가해질 때, 에너지 다이어그램등을 보여준다. 그림에서 $J_{s \rightarrow m}$와 $J_{m \rightarrow s}$는 각각 반도체에서 금속으로, 금속에서 반도체로 흐르는 전류밀도를 의미한다. $J_{s \rightarrow m}$를 먼저 구해보자. $J_{s \rightarrow m}$는 다음과 같이 주어진다. $$ J_{s \rightarrow m}=e \int_{E_c'}^{\infty} v_x d n \qquad (9.18) $$ 여기서 $E_c'$는 순전압일때 conduction 밴드의 최소값이고, $v_x$는 수송방향($x$ 방향)으로 운반자의 속도성분이다. 증분 전자농도($dn$)는 다음과 같이 주어진다. $$ d n=g_c(E) f_F(E) d E \qquad (9.19) $$ Maxwell-Boltzmann 근사에 의해 (4.5)식을 참고하면 다음을 얻는다. $$ d n=\frac{4 \pi\left(2 m_n^*\right)^{3 / 2}}{h^3} \sqrt{E-E_c'} \exp \left[\frac{-\left(E-E_F\right)}{k T}\right] d E \qquad (9.20) $$ $v_x$는 다음 관계식에서 얻을 수 있다. $$ \frac{1}{2} m_n^* v^2=E-E_c \qquad (9.21) $$ 주어진 조건들을 이용해서 (9.18)식을 다시 계산하고, 순 전류가 다음과 같이 주어진다는 것을 고려하면 $$ J=J_{s \rightarrow m}-J_{m \rightarrow s} \qquad (9.22) $$ 전류밀도는 다음과 같이 주어진다. $$ J=\left[A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right)\right]\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (9.23) $$ 여기서 $A^*$는 열전자 방출에 대한 유효 Richardson상수라고 한다. $$ A^* \equiv \frac{4 \pi e m_n^* k^2}{h^3} \qquad (9.24) $$ (9.23)식은 PN 접합의 전류식과 유사하게 다음과 같이 쓸수있다. $$ J = J_{s T}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (9.25) $$ 여기서 $J_{s T}$는 역포화 전류밀도이며 다음과 같이 주어진다. $$ J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right) \qquad (9.26) $$ 여기서 Schottky 장벽이 영상전하 효과에 의해 축소된다는 것을 알고 있다. $\phi_{B n} = \phi_{B 0} - \Delta \phi $을 적용하면 다음을 얻는다. \begin{equation} J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B 0}}{k T}\right) \exp \left(\frac{e \Delta \phi}{k T}\right) \qquad (9.27) \end{equation}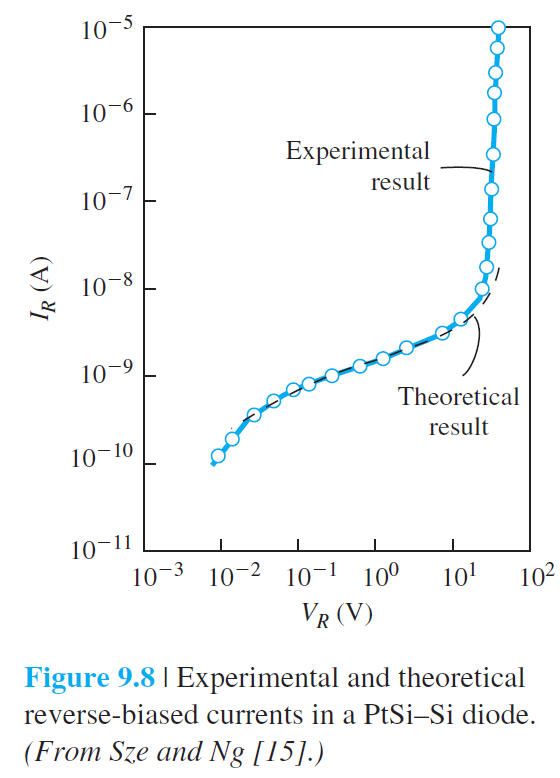
그림 9.8은 역전압에서 Schottky 다이오드의 전류-전압관계를 보여준다. 장벽 저하 효과때문에 역전압이 증가함에 따라 전류도 같이 증가하는 것을 볼수 있다.

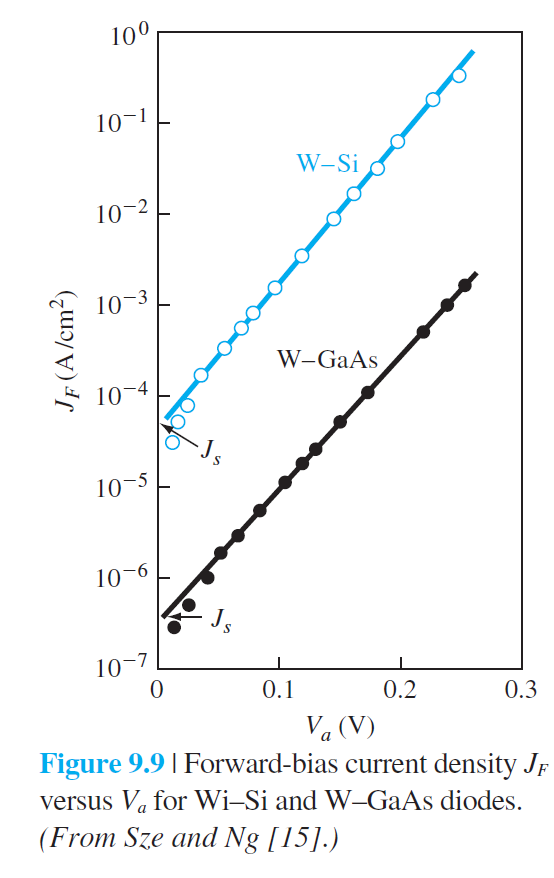
그림 9.9에는 순방향 전압에서 텅스텐-Si과 텅스텐-GaAs에 대한 전류-전압 관계를 보여준다. 이 그림에서 두 접합에 대한 역포화 전류밀도 값이 상당한 차이가 나는 것을 알수있다. 이것은 두 접합에서 장벽의 높이가 같다고 가정하면, 유효 Richardson상수의 차이를 반영하는 것이다. 유효 Richardson상수는 유효질량을 포함하고 있으므로, 그림 9.9에서 역포화전류의 차이는 유효질량의 차이를 상당히 반영한다고 볼수 있다.
• 열전자 방출(thermionic emission)
장벽의 높이가 $kT$보다 훨씬 크다는 가정을 통해 Maxwell-Boltzmann 근사 를 이용한다.

그림 9.7은 순전압 $V_a$가 가해질 때, 에너지 다이어그램등을 보여준다. 그림에서 $J_{s \rightarrow m}$와 $J_{m \rightarrow s}$는 각각 반도체에서 금속으로, 금속에서 반도체로 흐르는 전류밀도를 의미한다. $J_{s \rightarrow m}$를 먼저 구해보자. $J_{s \rightarrow m}$는 다음과 같이 주어진다. $$ J_{s \rightarrow m}=e \int_{E_c'}^{\infty} v_x d n \qquad (9.18) $$ 여기서 $E_c'$는 순전압일때 conduction 밴드의 최소값이고, $v_x$는 수송방향($x$ 방향)으로 운반자의 속도성분이다. 증분 전자농도($dn$)는 다음과 같이 주어진다. $$ d n=g_c(E) f_F(E) d E \qquad (9.19) $$ Maxwell-Boltzmann 근사에 의해 (4.5)식을 참고하면 다음을 얻는다. $$ d n=\frac{4 \pi\left(2 m_n^*\right)^{3 / 2}}{h^3} \sqrt{E-E_c'} \exp \left[\frac{-\left(E-E_F\right)}{k T}\right] d E \qquad (9.20) $$ $v_x$는 다음 관계식에서 얻을 수 있다. $$ \frac{1}{2} m_n^* v^2=E-E_c \qquad (9.21) $$ 주어진 조건들을 이용해서 (9.18)식을 다시 계산하고, 순 전류가 다음과 같이 주어진다는 것을 고려하면 $$ J=J_{s \rightarrow m}-J_{m \rightarrow s} \qquad (9.22) $$ 전류밀도는 다음과 같이 주어진다. $$ J=\left[A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right)\right]\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (9.23) $$ 여기서 $A^*$는 열전자 방출에 대한 유효 Richardson상수라고 한다. $$ A^* \equiv \frac{4 \pi e m_n^* k^2}{h^3} \qquad (9.24) $$ (9.23)식은 PN 접합의 전류식과 유사하게 다음과 같이 쓸수있다. $$ J = J_{s T}\left[\exp \left(\frac{e V_a}{k T}\right)-1\right] \qquad (9.25) $$ 여기서 $J_{s T}$는 역포화 전류밀도이며 다음과 같이 주어진다. $$ J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right) \qquad (9.26) $$ 여기서 Schottky 장벽이 영상전하 효과에 의해 축소된다는 것을 알고 있다. $\phi_{B n} = \phi_{B 0} - \Delta \phi $을 적용하면 다음을 얻는다. \begin{equation} J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B 0}}{k T}\right) \exp \left(\frac{e \Delta \phi}{k T}\right) \qquad (9.27) \end{equation}

그림 9.8은 역전압에서 Schottky 다이오드의 전류-전압관계를 보여준다. 장벽 저하 효과때문에 역전압이 증가함에 따라 전류도 같이 증가하는 것을 볼수 있다.

그림 9.9에는 순방향 전압에서 텅스텐-Si과 텅스텐-GaAs에 대한 전류-전압 관계를 보여준다. 이 그림에서 두 접합에 대한 역포화 전류밀도 값이 상당한 차이가 나는 것을 알수있다. 이것은 두 접합에서 장벽의 높이가 같다고 가정하면, 유효 Richardson상수의 차이를 반영하는 것이다. 유효 Richardson상수는 유효질량을 포함하고 있으므로, 그림 9.9에서 역포화전류의 차이는 유효질량의 차이를 상당히 반영한다고 볼수 있다.

9.1.5 Schottky 장벽 다이오드와 PN 접합 다이오드와의 비교
(9.25)식으로 주어지는 Schottky 장벽 다이오드의 전류-전압관계는 PN 접합 다이오드의 것과 유사하지만,
몇가지 중요한 차이가 있다.
첫째는 Schottky 장벽 다이오드의 전류는 다수 운반자의 열방출에 의래 결정되는데, PN 접합 다이오드의 전류는 소수 운반자의 확산에 의해 결정된다.
둘째는 역포화전류이며, 아래와 같이 다른 형태를 가지고 있다. $$ J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right) $$ $$ J_s=\frac{e D_n n_{p o}}{L_n}+\frac{e D_p p_{n o}}{L_p} \qquad (9.28) $$ PN 접합 다이오드의 역전압에서는 생성전류가 추가로 존재하지만, $10^{-7}$ A/cm^2 정도로 $J_{s T}$보다 $10^{-2} \sim 10^{-3}$만큼 매우 작은 값이다. 생성전류가 $J_s$ 보다도 더 크기 때문에 결과적으로 $J_{s T}$는 PN 접합 다이오드의 역전압 전류보다는 크다.
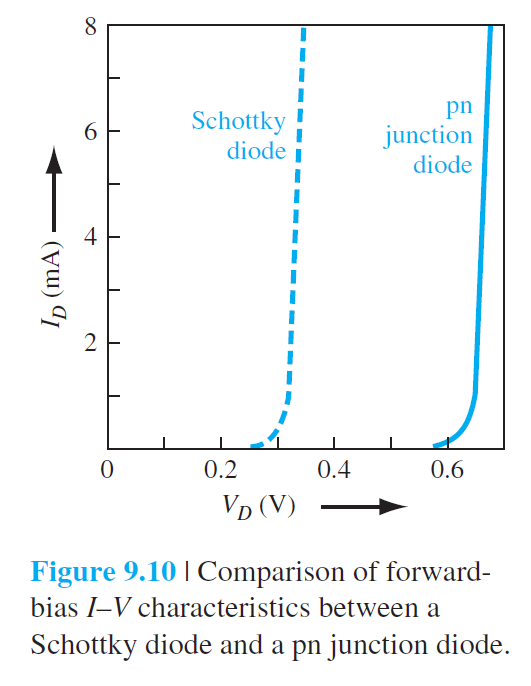
세째 이러한 역포화 전류의 큰 차이는 그림 9.10에서 보는 바와 같이 turn-on 전압에서 큰 차이를 일으키게 한다.
네째, 교류 전류의 특성에 차이가 생긴다. Schottky 장벽 다이오드의 순전압에서는 다수 운반자에 의한 전류가 흐르는데 이것은 순 방향전압에서는 확산 전기용량이 없다는 것을 의미한다. 이것은 PN접합 다이오드의 교류 특성에서 처럼 축적뙨 소수 운반자를 메울 필요가 없다는 것을 의미하기 때문에, Schottky 장벽 다이오드는 고속 스위칭 응용에 유리하다. PN 접합 다이오드의 스위칭 시간은 nano 초 범위인데, Schottky 장벽 다이오드의 스위칭 시간은 pico초 범위에 있다.

첫째는 Schottky 장벽 다이오드의 전류는 다수 운반자의 열방출에 의래 결정되는데, PN 접합 다이오드의 전류는 소수 운반자의 확산에 의해 결정된다.
둘째는 역포화전류이며, 아래와 같이 다른 형태를 가지고 있다. $$ J_{s T}=A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right) $$ $$ J_s=\frac{e D_n n_{p o}}{L_n}+\frac{e D_p p_{n o}}{L_p} \qquad (9.28) $$ PN 접합 다이오드의 역전압에서는 생성전류가 추가로 존재하지만, $10^{-7}$ A/cm^2 정도로 $J_{s T}$보다 $10^{-2} \sim 10^{-3}$만큼 매우 작은 값이다. 생성전류가 $J_s$ 보다도 더 크기 때문에 결과적으로 $J_{s T}$는 PN 접합 다이오드의 역전압 전류보다는 크다.
세째 이러한 역포화 전류의 큰 차이는 그림 9.10에서 보는 바와 같이 turn-on 전압에서 큰 차이를 일으키게 한다.

네째, 교류 전류의 특성에 차이가 생긴다. Schottky 장벽 다이오드의 순전압에서는 다수 운반자에 의한 전류가 흐르는데 이것은 순 방향전압에서는 확산 전기용량이 없다는 것을 의미한다. 이것은 PN접합 다이오드의 교류 특성에서 처럼 축적뙨 소수 운반자를 메울 필요가 없다는 것을 의미하기 때문에, Schottky 장벽 다이오드는 고속 스위칭 응용에 유리하다. PN 접합 다이오드의 스위칭 시간은 nano 초 범위인데, Schottky 장벽 다이오드의 스위칭 시간은 pico초 범위에 있다.


9.2 금속-반도체 ohmic 접촉
어떠한 소자든 외부와 접촉을 통해서 작동을 해야 한다.
외부와의 접촉은 저항성 접촉을 통해서 만들어지는 데,
가급적 저항이 적고 양방향으로 동일하고, 전압에 대한 선형적인 전류 특성을 가지면 좋다.
여기서는 두가지 저항성 접촉을 공부한다.
하나는 이상적인 비정류성 장벽이고 두번째는 투과 장벽이다.
9.2.1 이상적인 비정류성 장벽
우리는 $\phi_m > \phi_s$인 금속-반도체 접합에 대해 정류 특성이 나타남을 공부하였다.
이제 $\phi_m < \phi_s$인 금속-반도체 접합에 대한 에너지 다이어그램은 그림 11에 보여진다.
$E_F$은 금속쪽이 더 높기 때뭉에 접합 후 전자가 도체에서 반도체 쪽으로 이동하여,
곧 평형상태가 되면서 $E_F$가 전체 영역에서 동일한 높이가 된다.
이때 에너지 밴드들은 그림 11(b)처럼 휘어지게 된다.
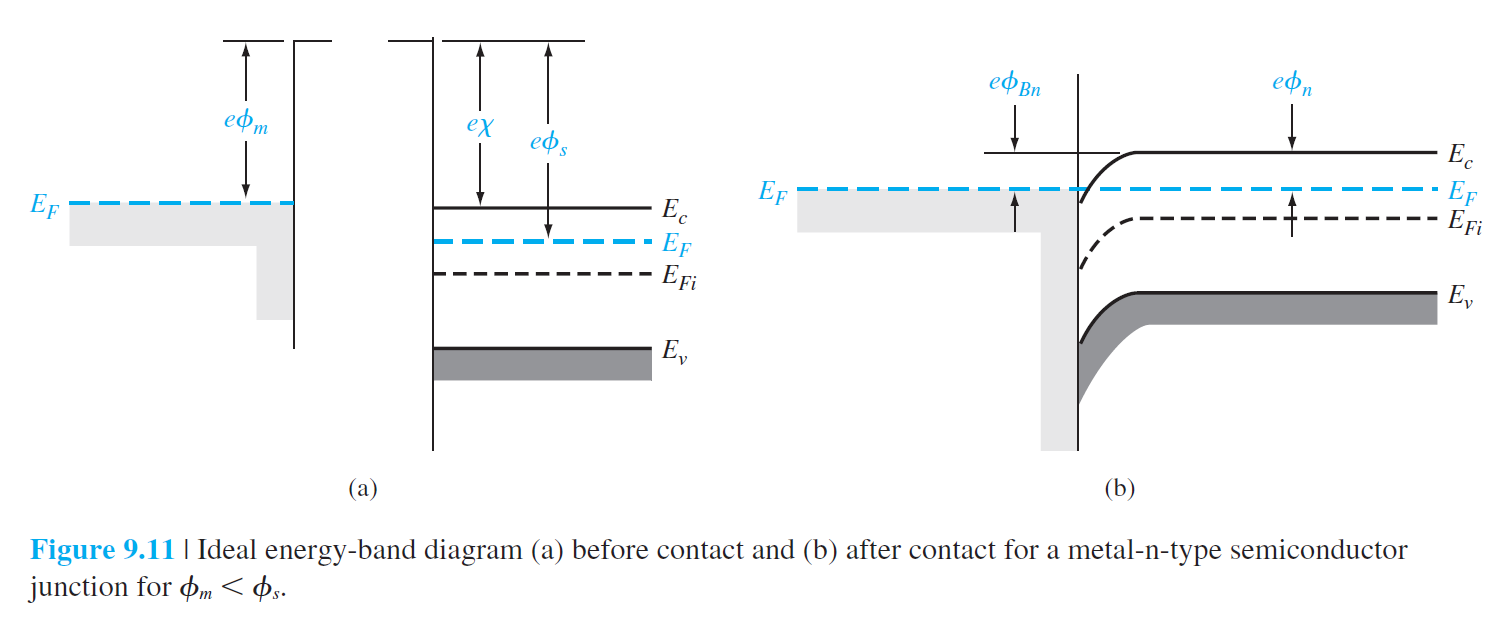
금속에서 봤을때 반도체 쪽에 장벽 $\phi_{Bn}$이 생기게 된다. 그림에서 이 장벽은 $\phi_{n}$과 같은데, 도핑을 충분히 한 경우 이 값은 매우 작다. 결과적으로 도핑을 충분히 한 경우에 장벽은 매우 작아진다고 할수있다. 그림 9.12는 전압을 양 방향으로 걸었을 때, 에너지 밴드를 보여준다. 어느 경우든 전자가 어떤 장벽없이 전류가 잘 흐르는 저항성 접촉을 보여준다.
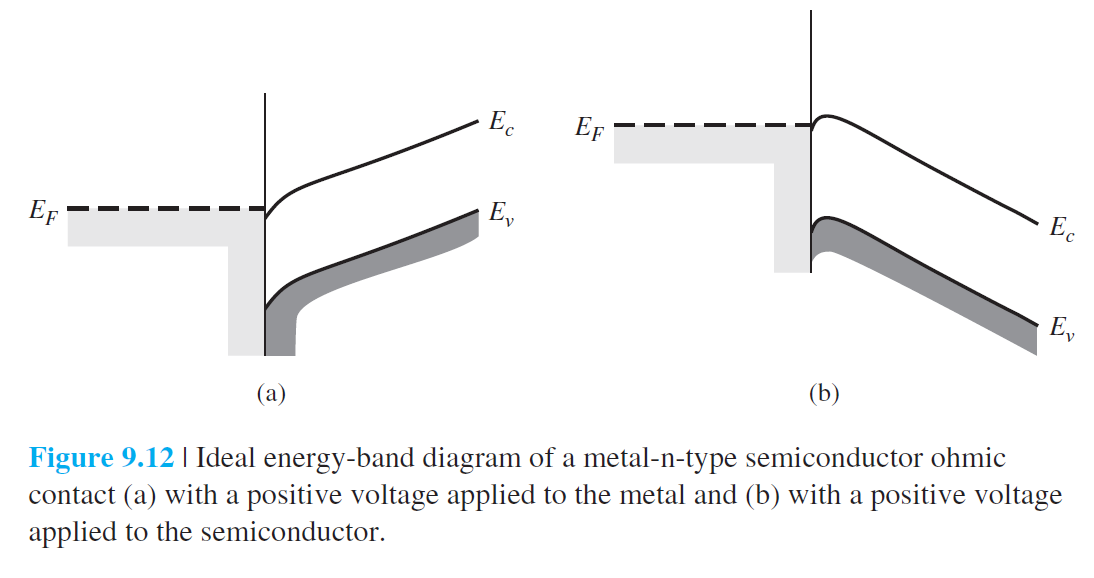
그림 9.13은 $\phi_m > \phi_s$인 금속-p형 반도체 접합에서 에너지 다이어그램을 보여준다. $E_F$은 반도체 쪽이 더 높기 때뭉에 접합 후 전자가 반도체에서 도체쪽으로 이동하여, 곧 평형상태가 되면서 $E_F$가 전체 영역에서 동일한 높이가 되고, 에너지밴드는 휘어지게 된다. 금속-n형 반도체 접합에서와 비슷한 논의로 이 경우에도 저항성 접촉이 된다.
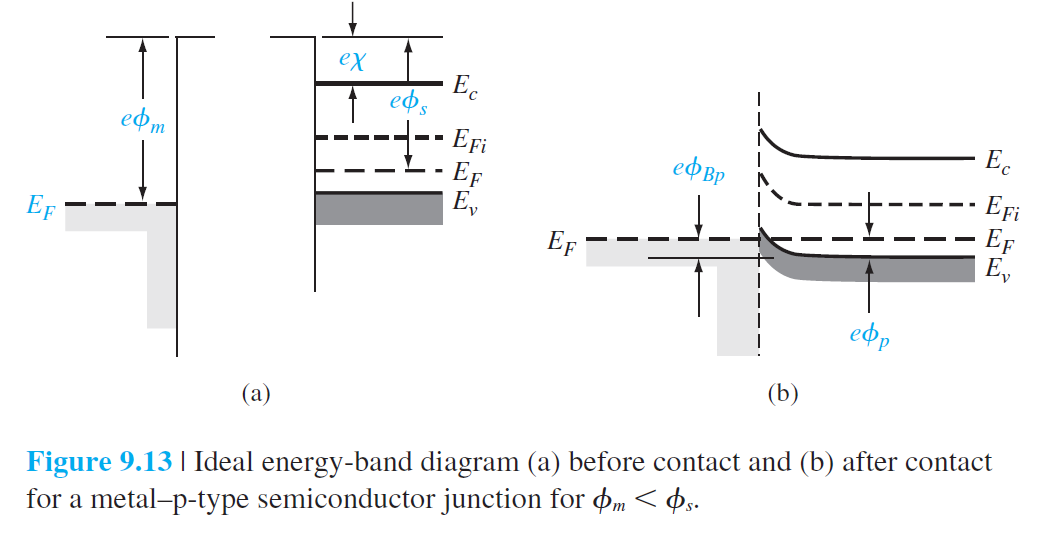
그림 9.11과 9.13은 표면 준위의 영향은 고려 하지 않았다. 그림 9.11에서 중성 준위가 $E_{Fi}$에 있다고 하면, $E_F$는 accpeptor 준위에 있게 될것이다. 그래서 표면 준위들은 음을 띄게 되는데, 이것은 에너지 다이어그램을 변형시킨다. 9.13도 마찬가지 인데, 이러한 이유로 표면 준위가 좋은 저항성 접촉에 방해가 될수도 있다.

금속에서 봤을때 반도체 쪽에 장벽 $\phi_{Bn}$이 생기게 된다. 그림에서 이 장벽은 $\phi_{n}$과 같은데, 도핑을 충분히 한 경우 이 값은 매우 작다. 결과적으로 도핑을 충분히 한 경우에 장벽은 매우 작아진다고 할수있다. 그림 9.12는 전압을 양 방향으로 걸었을 때, 에너지 밴드를 보여준다. 어느 경우든 전자가 어떤 장벽없이 전류가 잘 흐르는 저항성 접촉을 보여준다.

그림 9.13은 $\phi_m > \phi_s$인 금속-p형 반도체 접합에서 에너지 다이어그램을 보여준다. $E_F$은 반도체 쪽이 더 높기 때뭉에 접합 후 전자가 반도체에서 도체쪽으로 이동하여, 곧 평형상태가 되면서 $E_F$가 전체 영역에서 동일한 높이가 되고, 에너지밴드는 휘어지게 된다. 금속-n형 반도체 접합에서와 비슷한 논의로 이 경우에도 저항성 접촉이 된다.

그림 9.11과 9.13은 표면 준위의 영향은 고려 하지 않았다. 그림 9.11에서 중성 준위가 $E_{Fi}$에 있다고 하면, $E_F$는 accpeptor 준위에 있게 될것이다. 그래서 표면 준위들은 음을 띄게 되는데, 이것은 에너지 다이어그램을 변형시킨다. 9.13도 마찬가지 인데, 이러한 이유로 표면 준위가 좋은 저항성 접촉에 방해가 될수도 있다.
9.2.2 투과 장벽
(9.7)식에 의하면 공핍층의 폭은 $1/\sqrt{N_d}$에 비례한다.
이것은 반도체 내의 도핑이 증가할수록 공핍층의 폭과 장벽이 폭이 줄어드는 것을 의미한다.
장벽의 폭이 줄어들면 이 장벽을 투과할 확율이 증가하게 된다.
그림 9.14는 강하게 도핑된 n형 반도체 층이 금속과 접합되었을 때, 에너지 다이어그램을 보여준다.
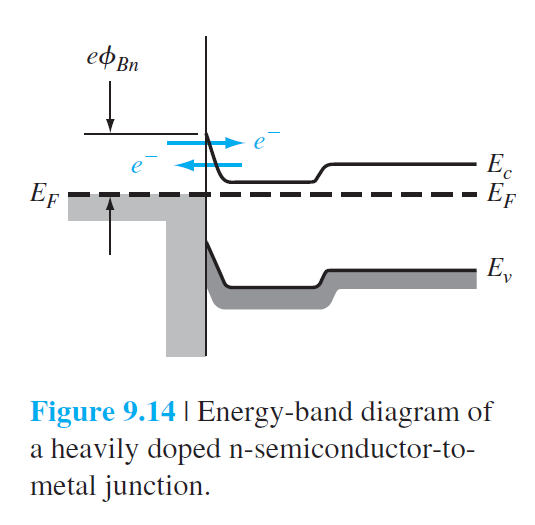
투과 전류는 다음과 같이 주어진다. $$ \begin{aligned} & J_t \propto \exp \left(\frac{-e \phi_{B n}}{E_{o o}}\right) \qquad (9.29) \\ & E_{o o}=\frac{e \hbar}{2} \sqrt{\frac{N_d}{\epsilon_s m_n^*}} \qquad (9.30) \end{aligned} $$

투과 전류는 다음과 같이 주어진다. $$ \begin{aligned} & J_t \propto \exp \left(\frac{-e \phi_{B n}}{E_{o o}}\right) \qquad (9.29) \\ & E_{o o}=\frac{e \hbar}{2} \sqrt{\frac{N_d}{\epsilon_s m_n^*}} \qquad (9.30) \end{aligned} $$

9.2.2 접촉 비저항
다음과 같이 정의되는 접촉 비저항 $R_c$는 저항성 접촉의 성능지수중 하나가 된다.
$R_c$가 낮을수록 우수한 저항성 접촉을 보인다고 할수있다.
$$
R_c=\left.\left(\frac{\partial J}{\partial V}\right)^{-1}\right|_{V=0} \quad \Omega-\mathrm{cm}^2 \qquad (9.31)
$$
이미 유도한 금속-반도체 접합에서 전류밀도는 (9.23)식으로 주어진다.
$$
J_n=A^* T^2 \exp \left(\frac{-e \phi_{B n}}{k T}\right)\left[\exp \left(\frac{e V}{k T}\right)-1\right]
$$
이 경우 접촉 비저항은 다음과 같다.
$$
R_c=\frac{\left(\frac{k T}{e}\right) \exp \left(\frac{+e \phi_{B n}}{k T}\right)}{A^* T^2} \qquad (9.32)
$$
접촉 비저항은 장벽 높이의 감소에 따라 급격히 감소한다.
높은 도핑농도에 의해 투과 과정이 우세한 경우 (9.29)식을 통해 접촉 비저항은 다음과 같이 주어진다.
$$
R_c \propto \exp \left(\frac{+2 \sqrt{\epsilon_s m_n^*}}{\hbar} \cdot \frac{\phi_{B n}}{\sqrt{N_d}}\right) \qquad (9.33)
$$
이것은 접촉 비저항과 도핑농도 사이의 관계를 직접적으로 보여준다.
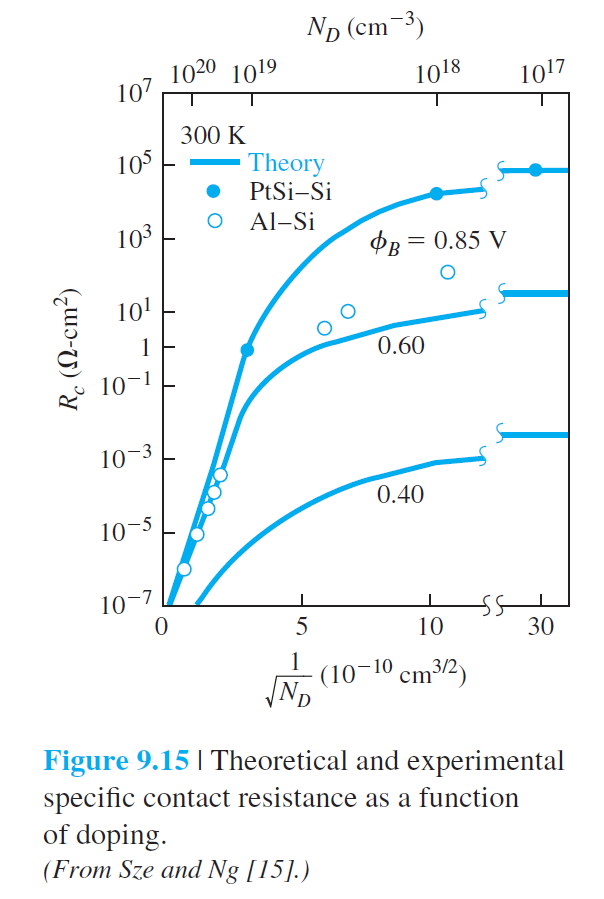
그림 9.15는 높은 도핑 농도에서 접촉 비저항이 $\exp(1/N_d)$의 관계를 가지는 것을 증명하고 있다.
결과적으로 양호한 저항성 접촉을 위해서는 반도체 쪽에 높은 도핑가 필요함을 알수있다.

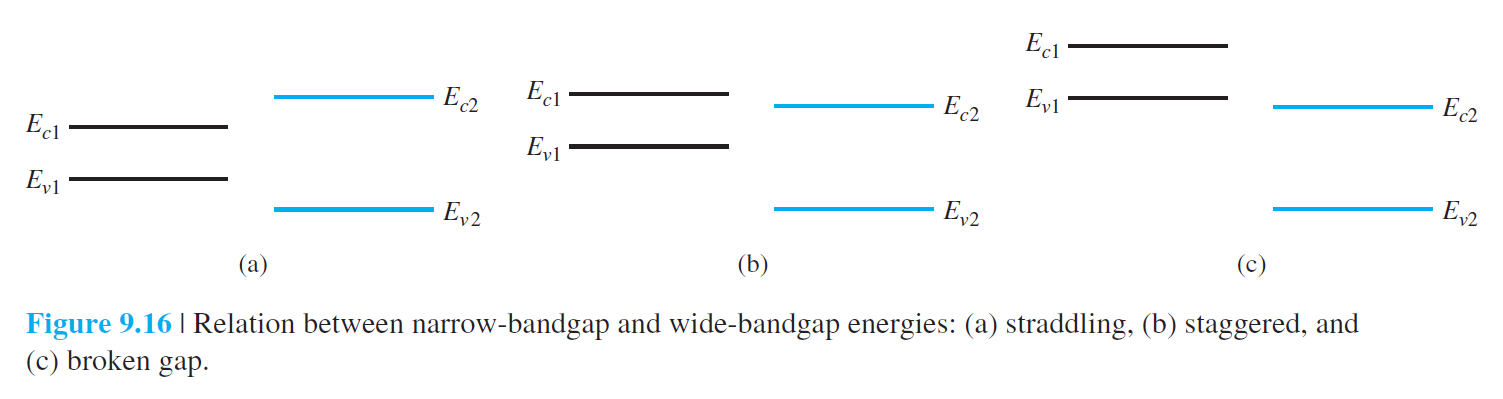
9.3 이종 접합
\begin{aligned}
&\Delta E_c=e\left(\chi_n-\chi_P\right) \qquad (9.34a)\\
&\Delta E_c+\Delta E_v=E_{g P}-E_{g n}=\Delta E_g \qquad (9.34b)
\end{aligned}
\begin{array}{ll}
V(x)=e E z & z > 0 \qquad (9.35a) \\
V(z)=\infty & z < 0 \qquad (9.35b)
\end{array}
\begin{equation}
V_{b i}=\phi_{s P}-\phi_{s n} \qquad (9.36)
\end{equation}
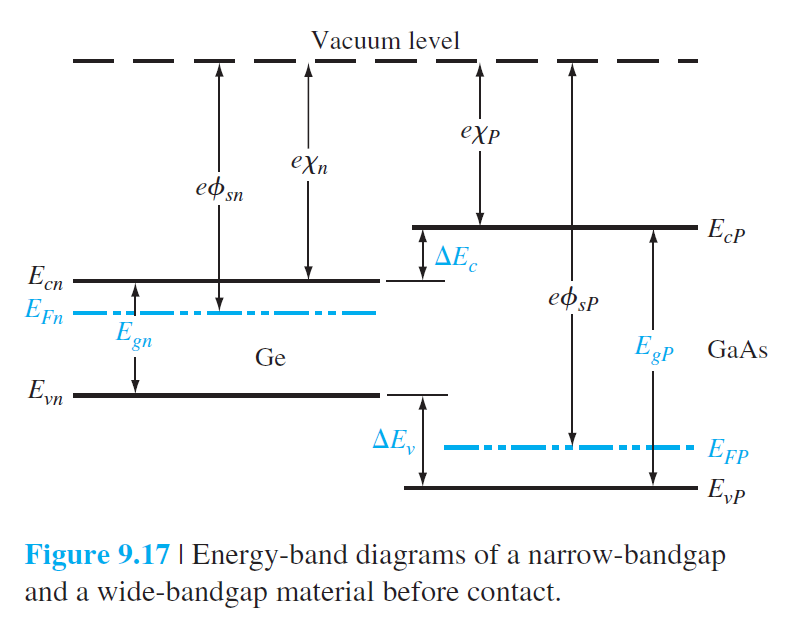
$$
\begin{aligned}
&e V_{b i}=\left[e \chi_P+E_{g P}-\left(E_{F P}-E_{v P}\right)\right]-\left[e \chi_n+E_{g n}-\left(E_{F n}-E_{v n}\right)\right] \\
&\qquad (9.37a)\\
&e V_{b i}=e\left(\chi_P-\chi_n\right)+\left(E_{g P}-E_{g n}\right)+\left(E_{F n}-E_{v n}\right)-\left(E_{F P}-E_{v P}\right) \\
&\qquad (9.37b)
\end{aligned}
$$
$$
e V_{b i}=-\Delta E_c+\Delta E_g+k T \ln \left(\frac{N_{v n}}{p_{n o}}\right)-k T \ln \left(\frac{N_{v P}}{p_{p o}}\right) \qquad (9.38)
$$
$$
e V_{b i}=\Delta E_v+k T \ln \left(\frac{p_{p o}}{p_{n o}} \cdot \frac{N_{v n}}{N_{v P}}\right) \qquad (9.39)
$$
$$
e V_{b i}=-\Delta E_c+k T \ln \left(\frac{n_{n o}}{n_{p o}} \cdot \frac{N_{c P}}{N_{c n}}\right) \qquad (9.40)
$$
$$
\begin{aligned}
& E_n=\frac{e N_{d n}}{\epsilon_n}\left(x_n+x\right) \quad\left(-x_n \leq x < 0\right) \qquad (9.41a)\\
& E_P=\frac{e N_{a P}}{\epsilon_P}\left(x_P-x\right) \quad\left(0 < x \leq x_P\right) \qquad (9.41b) \\
&
\end{aligned}
$$
$$
\epsilon_n E_n(x=0)=\epsilon_P E_P(x=0) \qquad (9.42a)
$$
$$
N_{d n} x_n=N_{a P} x_P \qquad (9.42b)
$$
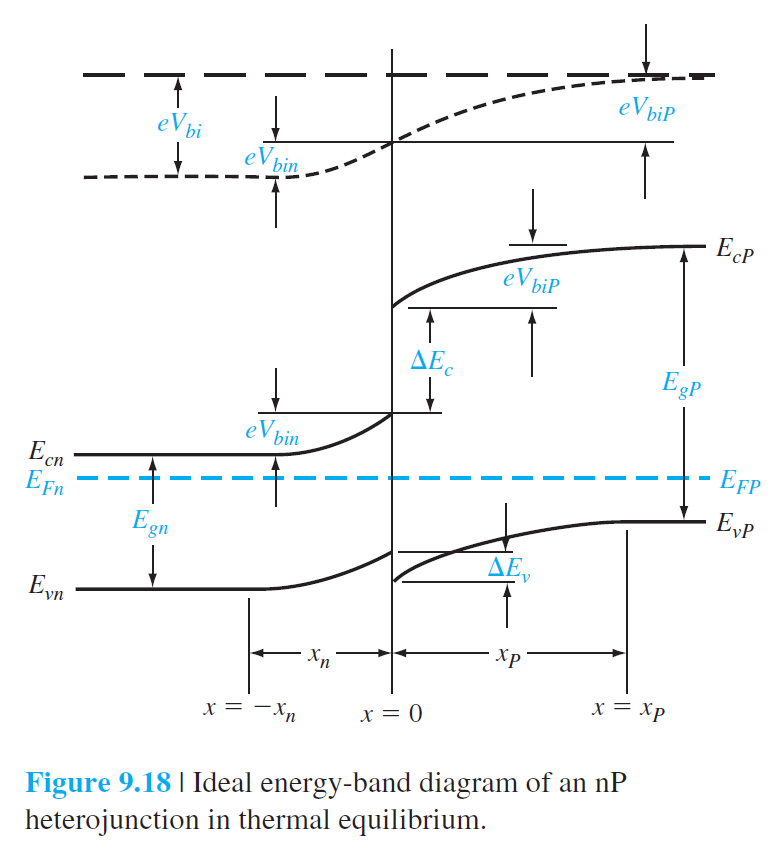
$$
\begin{gathered}
V_{b i n}=\frac{e N_{d n} x_n^2}{2 \epsilon_n} \qquad (9.43a)\\
V_{b i P}=\frac{e N_{a P} x_P^2}{2 \epsilon_P} \qquad (9.43b)
\end{gathered}
$$
$$
\frac{x_n}{x_P}=\frac{N_{a P}}{N_{d n}} \qquad (9.44)
$$
$$
\frac{V_{b i n}}{V_{b i P}}=\frac{\epsilon_P}{\epsilon_n} \cdot \frac{N_{d n}}{N_{a P}} \cdot \frac{x_n^2}{x_P^2}=\frac{\epsilon_P N_{a P}}{\epsilon_n N_{d n}} \qquad (9.45)
$$
$$
V_{b i}=V_{b i n}+V_{b i P}=\frac{e N_{d n} x_n^2}{2 \epsilon_n}+\frac{e N_{a P} x_P^2}{2 \epsilon_P} \qquad (9.46)
$$
$$
\begin{aligned}
& x_n=\left[\frac{2 \epsilon_n \epsilon_P N_{a P} V_{b i}}{e N_{d n}\left(\epsilon_n N_{d n}+\epsilon_P N_{a P}\right)}\right]^{1 / 2} \qquad (9.47a)\\
& x_P=\left[\frac{2 \epsilon_n \epsilon_P N_{d n} V_{b i}}{e N_{a P}\left(\epsilon_n N_{d n}+\epsilon_P N_{a P}\right)}\right]^{1 / 2} \qquad (9.47b)
\end{aligned}
$$
$$
W=x_n+x_P=\left[\frac{2 \epsilon_n \epsilon_P\left(N_{d n}+N_{a P}\right)^2 V_{b i}}{e N_{d n} N_{a P}\left(\epsilon_n N_{d n}+\epsilon_P N_{a P}\right)}\right]^{1 / 2} \qquad (9.48)
$$
$$
C_j'=\left[\frac{e N_{d n} N_{a P} \epsilon_n \epsilon_P}{2\left(\epsilon_n N_{d n}+\epsilon_P N_{a P}\right)\left(V_{b i}+V_R\right)}\right]^{1 / 2} \qquad (9.49)
$$
$$
\Delta E_c+\Delta E_v=\Delta E_g \qquad (9.50)
$$
\begin{equation}
J=A^* T^2 \exp \left(\frac{-E_w}{k T}\right) \qquad (9.51)
\end{equation}