9. 전자기유도

정전기학에서는 다음이 성립한다. $$ \begin{aligned} & \nabla \times \vec{E}=0 \\ & \oint \vec{E} \cdot d \vec{\ell}=0 \end{aligned} $$ 위 식이 의미하는 것은 폐경로 $C$를 따라 포텐셜의 변화가 있겠지만, 결국 제자리로 돌아왔을때는 원래의 포텐셜을 회복한다는 의미를 가지고 있다.
예를 들어서 전기장이 있는 진공 공간에 전자를 어떤 속도로 발사했을때, 전자가 처음에는 초기점으로부터 멀어지겠지만, 전기장의 영향을 받아 시간이 갈수록 초기점으로부터 멀어짐이 둔화되고 결국 초기점으로 돌아 오는 경우를 생각해 보자. 초기점으로 돌아 왔을때 전자는 처음의 포텐셜을 회복할것이다.
그러면 이러한 포텐셜 수준을 유지하면서 운동을 무한히 반복할 수 있다.
그러나 전자가 진공이 아닌 물질내에 있고, 동일한 상황에 놓인다면, 물질내의 저항에 의해서 초기위치로 돌아온다고 해도 원래의 포텐셜을 회복하지 못할 것이며, 이 운동을 무한히 반복할 수 없다. 만약에 물질의 저항에 의한 포텐셜 손실을 보충해줄 수 있는 요소가 매 회전마다 있다면, 이 운동을 다시 무한히 반복할 수 없다. 이 포텐셜 손실을 보충해줄 수 있는 요소를 기전력(electromotive force, emf) $\mathscr{E}$이라고 하며, 다음과 같이 정의된다. $$ \begin{aligned} \oint_C \vec{E} \cdot d \vec{\ell}=\mathscr{E} \\ \end{aligned} $$
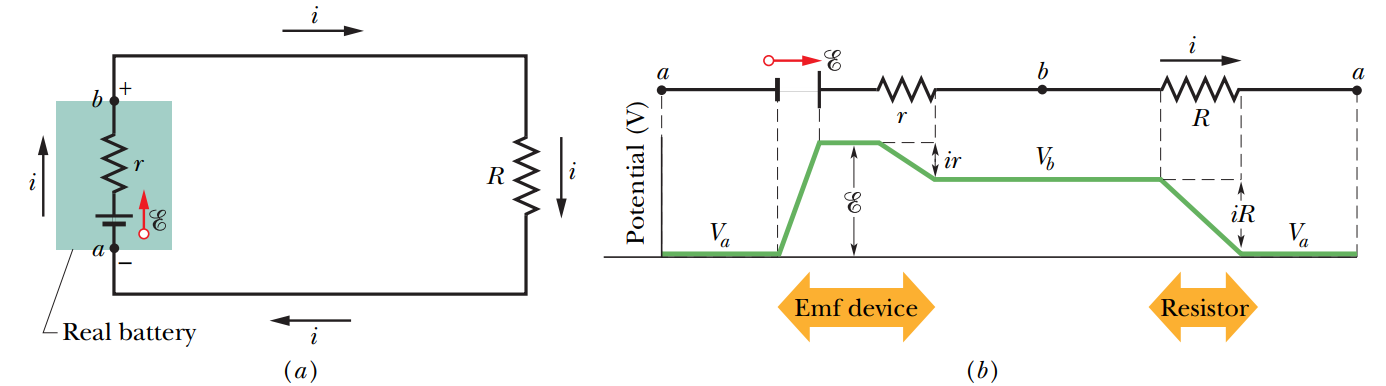
위 그림은 회로에서 기전력의 이해를 돕기 위해서 회로를 도식화한 그림이다.

9.1 Faraday의 법칙

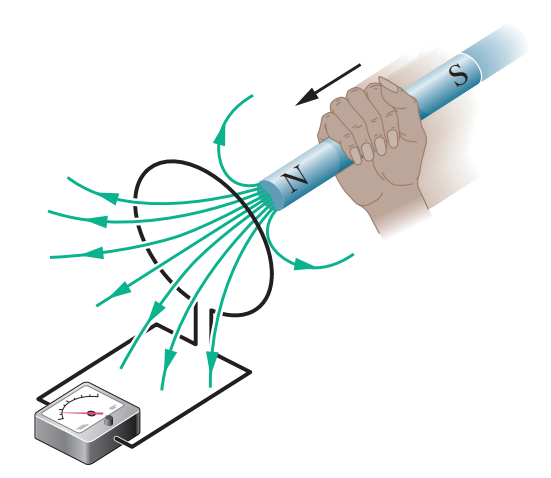
Faraday는 위 그림과 같이 회로 근처에서 자석의 이동에 따른 실험을 하였고, 이 결과를 아래와 같이 정리하였다. $$ \mathscr{E}=-\frac{d \Phi}{d t} $$ 위 식을 전자기유도에 대한 Faraday의 법칙이라고 한다.
즉 자기다발의 시간변화를 감소시키는 방향으로 유도 기전력이 발생한다.
기전력과 자기다발이 아래와 같이 주어지는 것을 이용하면, $$ \begin{aligned} \mathscr{E} & =\oint_C \vec{E} \cdot d \vec{\ell} \\ \Phi & =\int_S \vec{B} \cdot \hat{n} d a, \\ \oint_C \vec{E} \cdot d \vec{\ell} & =-\frac{d}{d t} \int_S \vec{B} \cdot \hat{n} d a . \end{aligned} $$ $$ \int_S \nabla \times \vec{E} \cdot \hat{n} d a=-\int_S \frac{\partial \vec{B}}{\partial t} \cdot \hat{n} d a . $$ 다음 식을 얻게 된다. $$ \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} $$ 위 식을 Faraday의 법칙의 미분형이라고 한다.
• Lenz의 법칙

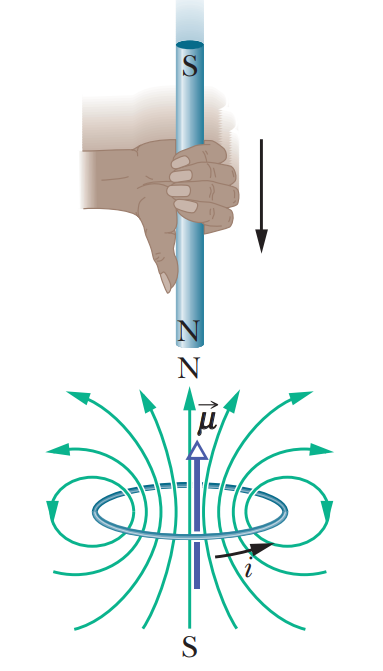
Lenz의 법칙의 법칙은 Faraday의 법칙의 약간 다른 표현인데, 자기다발의 변화를 억제하는 방향으로 기전력이 발생한다는 것이다. 다시말하면 자기 다발을 현상유지하려는 쪽으로 자기현상이 발생한다는 것이다.
• 자기다발이 변하는 3가지 경우
Faraday의 법칙을 더 잘 이해하기 위해 회로를 통과하는 자기장이 균일한 경우로 단순화헤 보자. 그러면 회로를 통과하는 자기다발은 다음과 같이 주어진다. $$ \begin{aligned} \Phi &=\int_S \vec{B} \cdot \hat{n} d a \\ & = \vec{B} \cdot \vec{A} = B A \cos\theta \\ \end{aligned} $$ 위와 같이 시간에 따라 자기다발이 변한다면, 변하는 요소는 $B$, $A$, $\theta$ 이 세가지일 것이다.
(예제) $B$가 변하는 경우

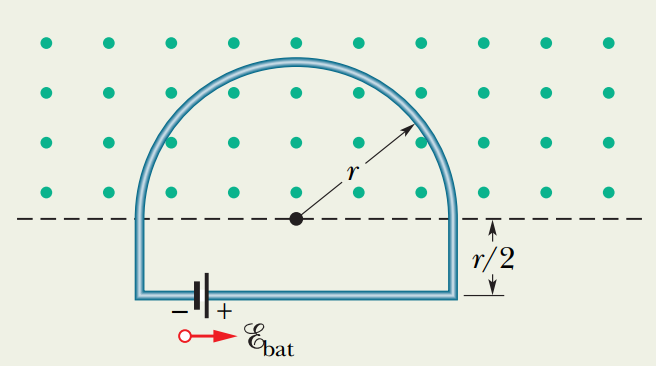
위 그림은 반지름 $r= 0.20$m의 반원과 세 개의 직선 섹션으로 구성된 폐회로를 보여준다. 반원은 화면에서 나오는 방향으로 향하는 균일한 자기장 안에 있으며, 자기장 크기는 $B = 4.0t^2 + 2.0t +3.0$ T로 표시된다. 기전력 2.0V의 배터리가 회로에 연결되어 있다. 루프의 저항은 2.0 $\Omega$입니다.
(a) t=10초에서 유도되는 기전력의 크기와 방향은?
$$ \mathscr{E}_{\mathrm{ind}}=\frac{d \Phi_B}{d t}=\frac{d(B A)}{d t}=A \frac{d B}{d t} $$ $$ \begin{aligned} \mathscr{E}_{\text {ind }} & =A \frac{d B}{d t}=\frac{\pi r^2}{2} \frac{d}{d t}\left(4.0 t^2+2.0 t+3.0\right) \\ & =\frac{\pi r^2}{2}(8.0 t+2.0) \end{aligned} $$ $$ \begin{aligned} \mathscr{E}_{\text {ind }} & =\frac{\pi(0.20 \mathrm{~m})^2}{2}[8.0(10)+2.0] \\ & =5.152 \mathrm{~V} \approx 5.2 \mathrm{~V} . \end{aligned} $$
(b) t=10초에서 회로의 전류는 얼마인가?
$$ \begin{aligned} i & =\frac{\mathscr{E}_{\text {net }}}{R}=\frac{\mathscr{E}_{\text {ind }}-\mathscr{E}_{\text {bat }}}{R} \\ & =\frac{5.152 \mathrm{~V}-2.0 \mathrm{~V}}{2.0 \Omega}=1.58 \mathrm{~A} \approx 1.6 \mathrm{~A} . \end{aligned} $$ (예제) $A$가 변하는 경우

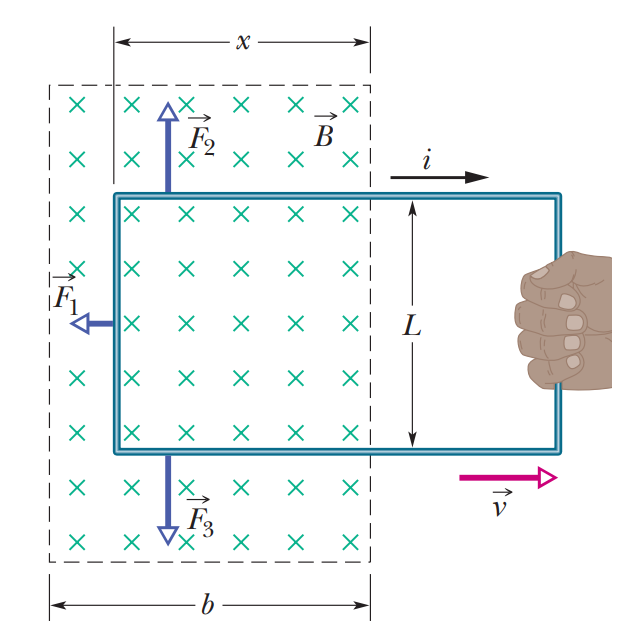
그림과 같이 시간에 불변이고 균일한 자기장 $B$가 화면에서 들어가는 방향으로 가해지는 공간에 사각의 도선이 걸처있다. 이 도선을 일정한 속도 $v$로 외부로 끌어당기면, 자기다발의 시간변화는 다음과 같다. $$ \frac{d\Phi}{dt} = \frac{d(B A)}{dt} = B \frac{d(xL)}{dt} = BLv $$ 그러면 유도기전력의 크기는 다음과 같다. $$ \mathscr{E} = BLv $$ 도선이 외부로 끌어 당겨지면, 도선을 통과하는 자기다발이 감소하므로 그것을 방해하기 위한 방향인 시계방향으로 기전력이 발생하게 된다.
• Eddy current(와전류)


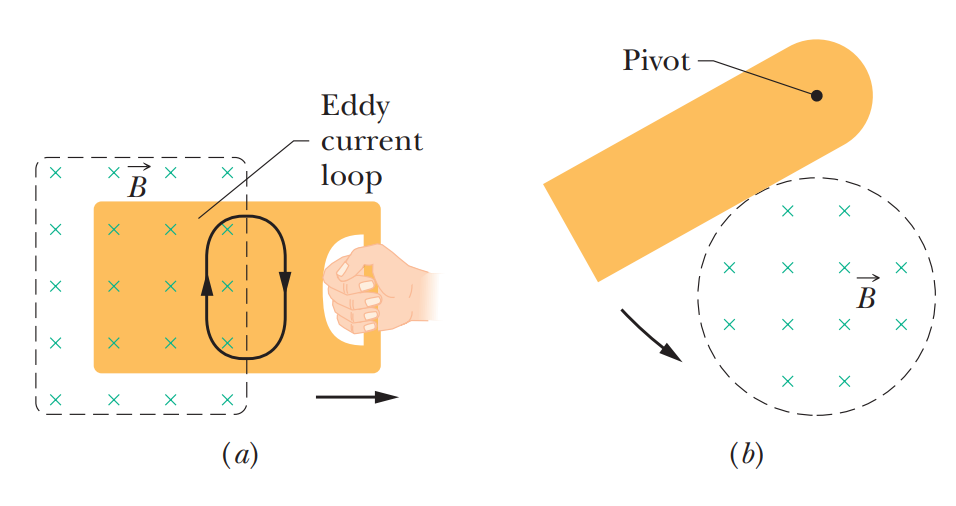
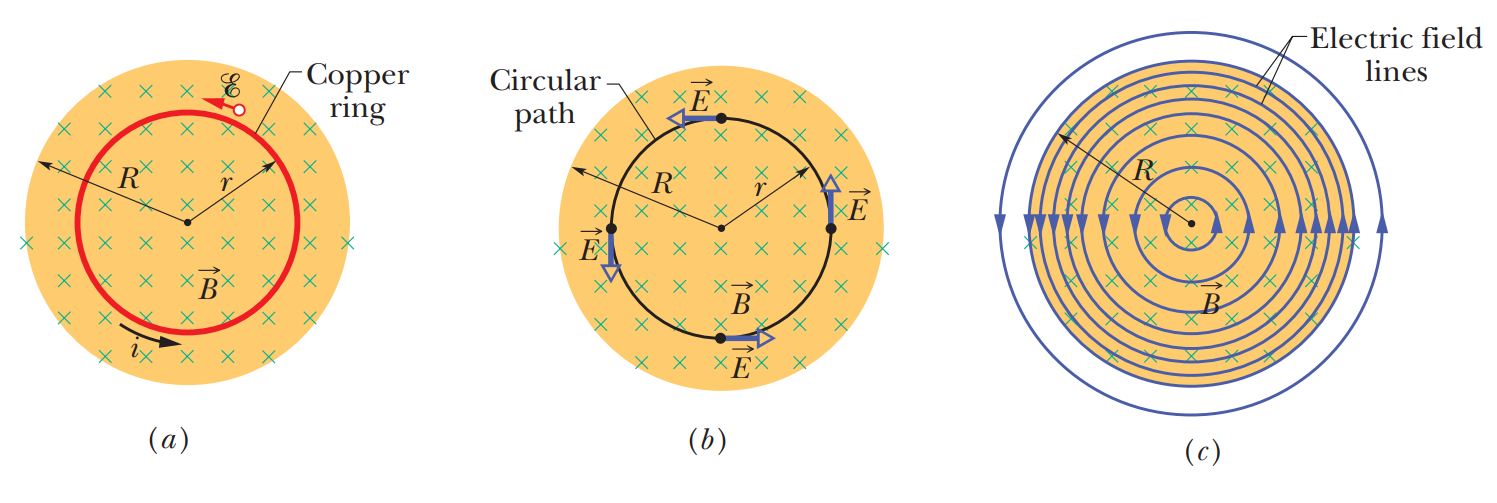
위 그림처럼 기전력의 실체는 전기장이다.
(예제) $\theta$가 변하는 경우

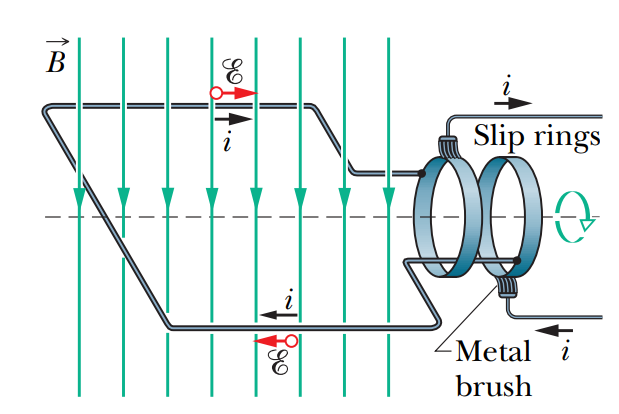
그림과 같이 시간에 불변이고 균일한 자기장 $B$가 가해지고 있는 공간에, 면적이 $A$인 폐회로가 있다.
이 폐회로가 축을 중심으로, $f$ Hz의 진동수로 회전하면, 회로를 통과하는 자기다발의 시간변화와 기전력은 다음과 같다. $$\mathscr{E} = \frac{d\Phi}{dt} = \frac{d(B A \cos(2\pi f t))}{dt} = - BA(2\pi f) \sin(2\pi f t) $$

9.2 자체 인덕턴스(self inductnace)

• 자체 인덕턴스의 정의
자체 인덕턴스는 다음과 같이 정의된다. $$ \frac{d \Phi}{d t}=\frac{d \Phi}{d I} \frac{d I}{d t} $$ $$ L=\frac{d \Phi}{d I} $$ $$ \mathscr{E} = -L \frac{d I}{d t} $$ 인덕턴스의 단위는 H(Henry)이다.
• R-L 회로
자체 인턱턴스가 어떤 역할을 하는지 알아보기 위해 R-L 회로를 살펴보자.

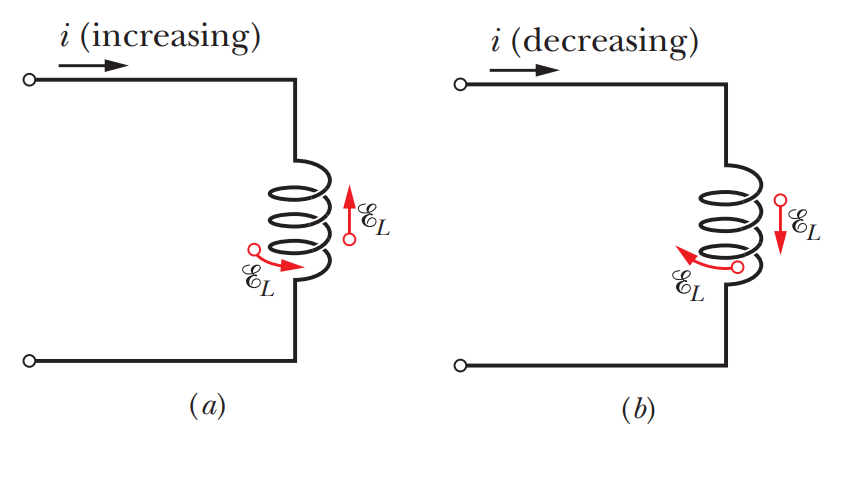
우선 인덕턴스 코일은 위 그림과 같이 전류의 변화를 방해한다.

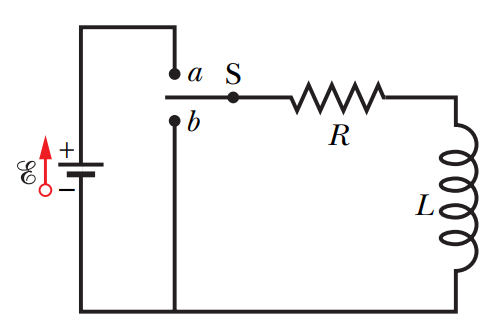
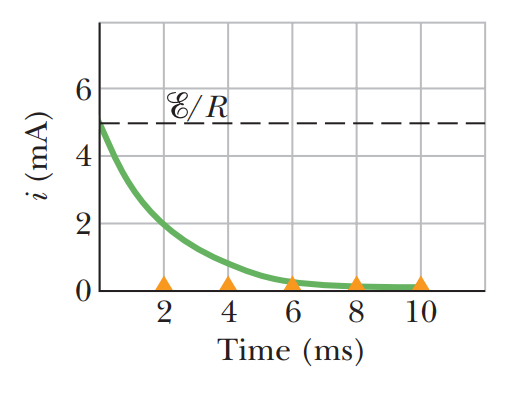
그래서 위 회로에서 건전지에 R-L 회로를 연결하거나 단절할때 즉각적으로 전류가 흐르거나 멈추지 않고, 아래 그림 처럼 지수함수적으로 서서히 포화상태에 이르게 된다.

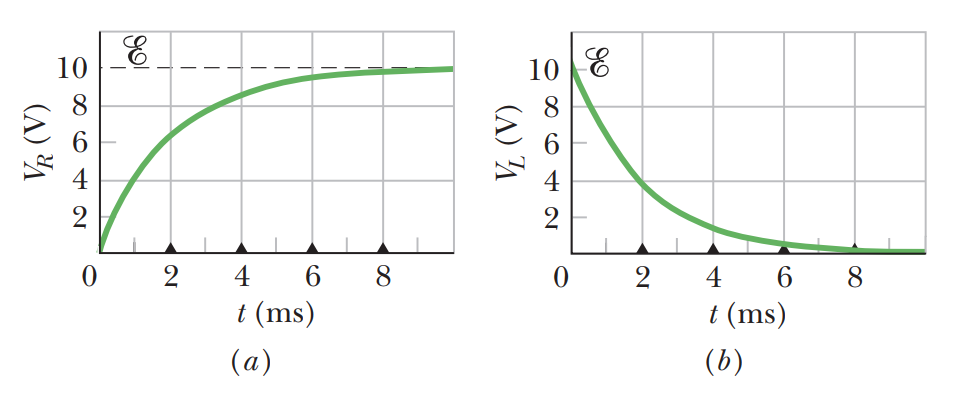
즉 자체 인덕턴스가 클수록 전류의 변화를 더 크게 방해한다.
$$ -i R-L \frac{d i}{d t}+\mathscr{E}=0 $$ $$ L \frac{d i}{d t}+R i=\mathscr{E} $$ $$ i=\frac{\mathscr{E}}{R}\left(1-e^{-R t / L}\right), $$ $$ i=\frac{\mathscr{E}}{R}\left(1-e^{-t / \tau_L}\right) $$ $$ \tau_L=\frac{L}{R} $$ • 미분 방정식의 풀이
\begin{aligned} L \frac{d i}{d t}+R i=\mathscr{E} \end{aligned} 위 식을 좀 더 정리하면 \begin{equation} \begin{aligned} & \frac{d i}{d t}=\frac{1}{L}(\mathscr{E}-R i) \\ & \frac{L}{R} \frac{d i}{i-\mathscr{E} / R}=-d t \\ & \frac{L}{R} \int \frac{d i}{i-\mathscr{E} / R}=-t+C \end{aligned} \end{equation} \begin{equation} \begin{aligned} & \frac{L}{R} \ln \left(i-\frac{\mathscr{E}}{R}\right)=-t+C \\ & \ln \left(i-\frac{\mathscr{E}}{R}\right)=-\frac{R}{L} t + C' \\ & i-\frac{\mathscr{E}}{R}=C'' e^{-\frac{R}{L} t} \\ & i=\frac{\mathscr{E}}{R}-C'' e^{-\frac{R}{L} t} \end{aligned} \end{equation} $t=0$에서 $i=0$이므로 계수 $C''$는 $\frac{\mathscr{E}}{R}$ 로 결정된다. 그러므로 다음이 성립한다. \begin{equation} \begin{aligned} i=\frac{\mathscr{E}}{R}\left(1-e^{-\frac{R}{L} t}\right) \end{aligned} \end{equation} • R-C 회로


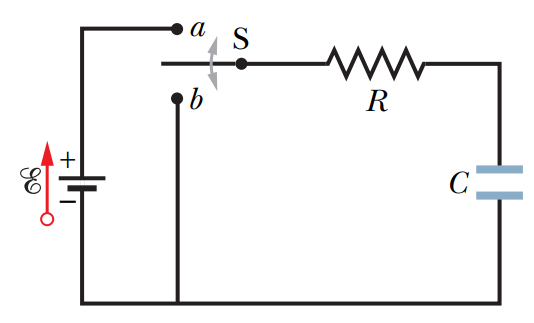
• R-L-C 회로
• 자체 인덕턴스의 계산

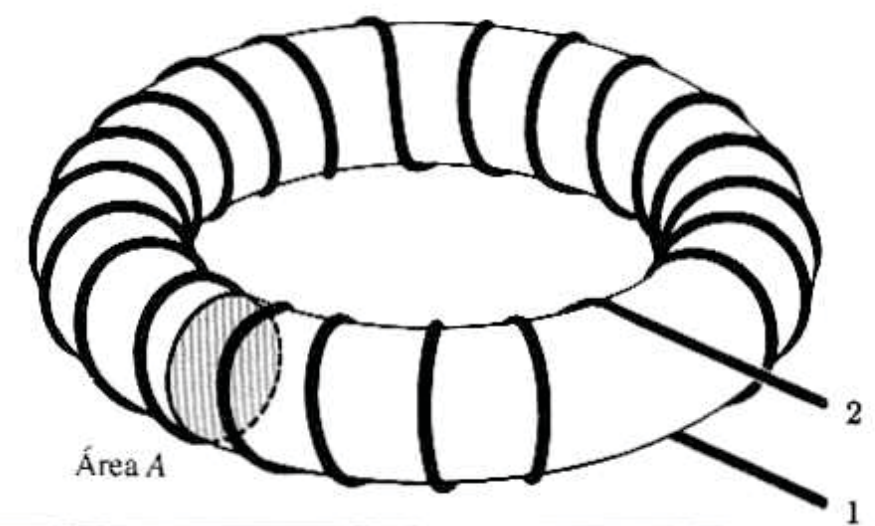
그림과 같이 전류 $I$가 흐르고 $N$번 감긴 toroid의 자체 인덕턴스는 다음과 같이 계산된다.
$$ B=\frac{\mu_0 N I}{l} $$ $$ \Phi_1=\frac{\mu_0 N I A}{l} $$ $$ \Phi=\frac{\mu_0 N^2 A}{l} I . $$ $$ L=\frac{d \Phi}{d I}=\frac{\mu_0 N^2 A}{l} . $$

9.3 상호 인덕턴스(mutual inductnace)

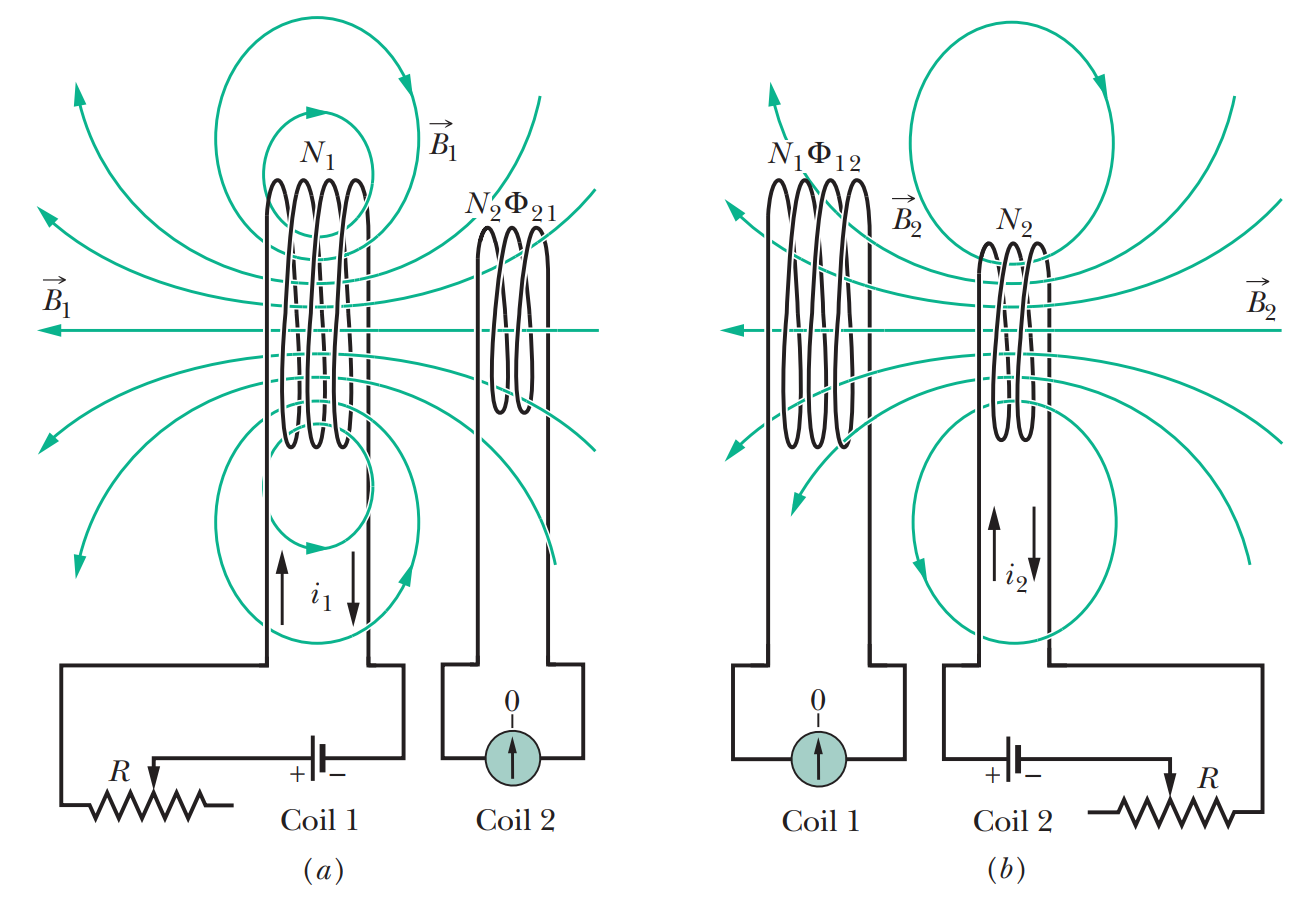
그림과 같이 인접한 고리 회로가 만드는 자기장에 의해 유도 기전력이 발생할 수 있는데, 이 경우 상호 인덕턴스(mutual inductnace)를 정의할 수 있다.
$n$개의 고리 회로가 있는 일반적인 상황을 생각해 보자. 다른 고리들이 만드는 $i$번째 회로를 통과하는 자기다발은 다음과 같이 주어진다. $$ \Phi_i=\Phi_{i 1}+\Phi_{i 2}+\cdots+\Phi_{i i}+\cdots+\Phi_{i n}=\sum_{j=1}^n \Phi_{i j} $$ 여기서 $\Phi_{i 1}$은 1번째 회로가 만드는 자기장이 $i$번째 회로를 통과하며 만드는 자기다발이다.
$i$번째 회로에 발생하는 유도기전력은 다음과 같이 주어진다. $$ \mathscr{E}_i=-\frac{d \Phi_i}{d t}=-\left\{\frac{d \Phi_{i 1}}{d t}+\cdots+\frac{d \Phi_{i i}}{d t}+\cdots+\frac{d \Phi_{i n}}{d t}\right\}=-\sum_{j=1}^n \frac{d \Phi_{i j}}{d t} $$ 여기서 상호 인덕턴스는 다음과 같이 정의된다. $$ \frac{d \Phi_{i j}}{d t}=\frac{d \Phi_{i j}}{d I_j} \frac{d I_j}{d t} . $$ $$ M_{i j}=\frac{d \Phi_{i j}}{d I_j}, \quad i \neq j $$ (예제) 전류 $I_1$과 $N_1$번 감긴, 전류 $I_2$와 $N_2$번 감긴 두 개의 toroid가 겹쳐 있다고 가정해 보자.
이 경우 상호 인덕턴스를 구해보자.
toroid 1 내부의 B는 다음과 같이 주어진다. $$ B=\frac{\mu_0 N_1 I_1}{l}, $$ 이 자기장이 toroid 1인 자기 자신과 toroid 2를 통과할 것이다.
각 toroid를 통과하는 자기다발은 각각 다음과 같이 주어지고, $$ \Phi_{11}=\frac{\mu_0 N_1^2 A I_1}{l} $$ $$ \Phi_{21}=\frac{\mu_0 N_1 N_2 A I_1}{l} $$ 자체 인덕턴스와 상호 인덕턴스는 다음과 같이 주어진다. $$ L_1=\frac{\mu_0 N_1^2 A}{l} $$ $$ M_{21}=\frac{\mu_0 N_1 N_2 A}{l} $$ $$ \begin{gathered} L_2=\frac{\mu_0 N_2^2 A}{l}, \\ M_{12}=\frac{\mu_0 N_1 N_2 A}{l}, \end{gathered} $$ 위 결과들로부터 다음을 알 수 있다. $$ M_{12}=\sqrt{L_1 L_2} $$ 일반적으로 상호 인덕턴스는 다음과 같은 범위를 가진다. $$ M=k \sqrt{L_1 L_2}, \quad-1 \leq k \leq 1 $$

9.4 연결된 인덕턴스

• 직렬 연결

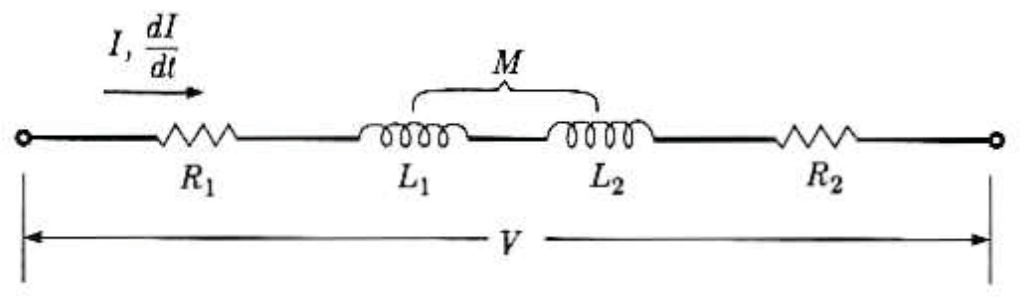
$$ \begin{gathered} V+\mathscr{E}_1+\mathscr{E}_2=R_1 I+R_2 I \\ V=R_1 I+L_1 \frac{d I}{d t}+M \frac{d I}{d t}+R_2 I+L_2 \frac{d I}{d t}+M \frac{d I}{d t} \end{gathered} $$ $$ V=\left(R_1+R_2\right) I+\left(L_1+L_2+2 M\right) \frac{d I}{d t} $$ $$ M=k \sqrt{L_1 L_2}, \quad-1 \leq k \leq 1 . $$ $$ L_{\mathrm{eff}}=L_1+2 k \sqrt{L_1 L_2}+L_2 . $$ • 병렬 연결

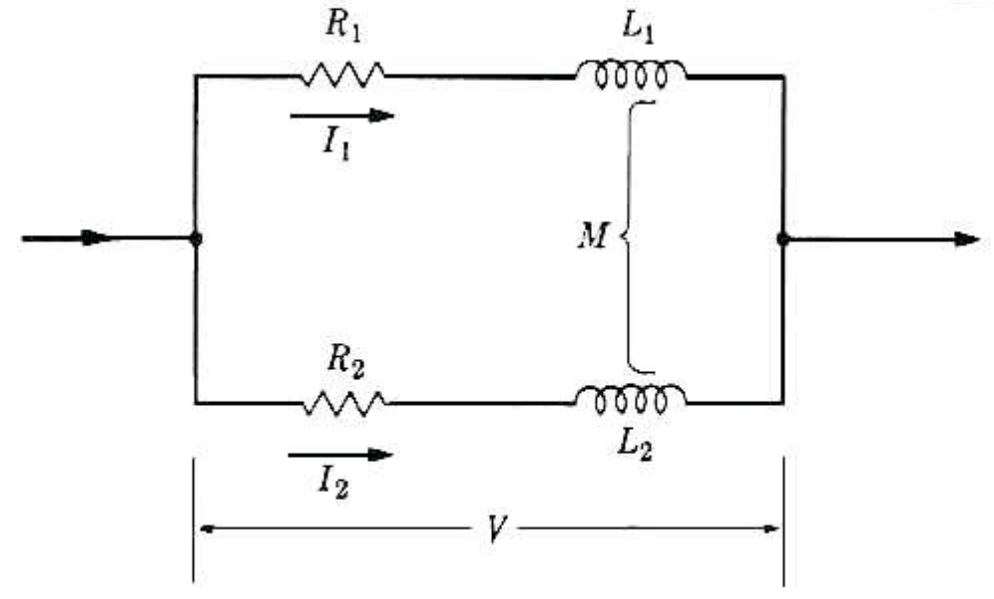
$$ \begin{aligned} & V=L_1 \frac{d I_1}{d t}+M \frac{d I_2}{d t} \\ & V=L_2 \frac{d I_2}{d t}+M \frac{d I_1}{d t} . \end{aligned} $$ $$ \begin{aligned} & V\left(L_2-M\right)=\left(L_1 L_2-M^2\right) \frac{d I_1}{d t} \\ & V\left(L_1-M\right)=\left(L_1 L_2-M^2\right) \frac{d I_2}{d t} \end{aligned} $$ $$ V=\frac{L_1 L_2-M^2}{L_1+L_2-2 M} \frac{d I}{d t} . $$ $$ L_{\mathrm{eff}}=\frac{L_1 L_2-M^2}{L_1+L_2-2 M} $$

9.5 Neumann 공식

Neumann 공식으로부터 두 회로의 세부모양이 반영된 상호인덕턴스를 구할 수 있다. $$ M_{21}=\frac{\Phi_{21}}{I_1} $$ $$ \begin{aligned} \Phi_{21} &=\frac{\mu_0}{4 \pi} I_1 \int_{S_2}\left\{\oint_{C_1} \frac{d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3}\right\} \cdot \hat{n} d a_2 \\ &\oint_{C_1} \frac{d \vec{\ell}_1 \times\left(\vec{r}_2-\vec{r}_1\right)}{\left|\vec{r}_2-\vec{r}_1\right|^3}=\nabla_2 \times \oint_{C_1} \frac{d \vec{\ell}_1}{\left|\vec{r}_2-\vec{r}_1\right|} \\ M_{21}&=\frac{\Phi_{21}}{I_1}=\frac{\mu_0}{4 \pi} \int_{S_2} \nabla_2 \times\left\{\oint_{C_1} \frac{d \vec{\ell}_1}{\left|\vec{r}_2-\vec{r}_1\right|}\right\} \cdot \hat{n} d a_2 \end{aligned} $$ $$ M_{21}=\frac{\mu_0}{4 \pi} \oint_{C_2} \oint_{C_1} \frac{d \vec{\ell}_1 \cdot d \vec{\ell}_2}{\left|\vec{r}_2-\vec{r}_1\right|}, $$ $$ L=\frac{\mu_0}{4 \pi} \oint_{C_1} \oint_{C_1} \frac{d \vec{\ell}_1 \cdot d \vec{\ell}_1^{\prime}}{\left|\vec{r}_1-\vec{r}_1^{\prime}\right|} $$